вращающееся магнитное поле это

Вращающееся магнитное поле

Вращающееся магнитное поле. Обычно под вращающимся магнитным полем понимается магнитное поле, вектор магнитной индукции которого, не изменяясь по модулю, вращается с постоянной угловой скоростью. Впрочем, вращающимися называют и магнитные поля магнитов, вращающихся относительно оси, не совпадающей с их осью симметрии (например, магнитные поля звезд или планет).

Вращающееся магнитное поле создают, накладывая два или более разнонаправленных переменных, зависящих от времени по синусоидальному закону, магнитных поля одинаковой частоты, но сдвинутых друг относительно друга по фазе.

Это было на практике осуществлено независимо в 1882 году сербским инженером Н. Тесла и, немного позже, итальянским физиком Г. Феррарисом. Применяется в синхронных и асинхронных машинах.

Разность фаз для двухфазных систем (два перпендикулярных электромагнита) должна составлять 90°, а для 3-фазных (три электромагнита, направленных в одной плоскости под углом 120° друг к другу) 120°.

Патенты

Полезное

Смотреть что такое «Вращающееся магнитное поле» в других словарях:

ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ — магнитное поле, вектор магнитной индукции которого вращается в пространстве с постоянной частотой. Получают сложением 2 и более переменных магнитных полей, сдвинутых во времени и пространстве. Используется во многих машинах переменного тока,… … Большой Энциклопедический словарь

ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ — поле, магнитный поток которого (вектор магнитной индукции) вращается в пространстве с постоянной частотой вокруг некоторой оси. Возникает при сложении двух и более переменных магнитных полей, сдвинутых во времени и пространстве. Наибольшее… … Большая политехническая энциклопедия

вращающееся магнитное поле — магнитное поле, вектор магнитной индукции которого вращается в пространстве с постоянной частотой. Получают сложением двух и более переменных магнитных полей, сдвинутых во времени и пространстве. Используется во многих машинах переменного тока,… … Энциклопедический словарь

Вращающееся магнитное поле — возникает как результирующее поле при наложении двух или более переменных магнитных полей, имеющих одинаковую частоту, но сдвинутых одно относительно другого по фазе в пространстве. Явление В. м. п., которое впервые в строгой научной… … Большая советская энциклопедия

ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ — магн. поле, вектор магн. индукции к рого вращается в пространстве с пост. частотой. Получают сложением 2 и более переменных магн. полей, сдвинутых во времени и пространстве. Используется во мн. машинах перем. тока, измерит. приборах и др … Естествознание. Энциклопедический словарь

Вращающееся магнитное поле микросборки ЦМД — 72. Вращающееся магнитное поле микросборки ЦМД Вращающееся магнитное поле Rotating magnetic field Магнитное поле, вектор напряженности которого вращается в плоскости ЦМД кристалла, служащее для продвижения цилиндрических магнитных доменов… … Словарь-справочник терминов нормативно-технической документации

Магнитное поле — Классическая электродинамика … Википедия

ПОЛЕ — (1) (см. (13)), существующее в виде (см.) и описываемое совокупностью пространственно временных распределений физ. величин, характеризующих рассматриваемые волны; (2) П. вращающееся магнитное ] (3) П. голографическое волновое поле (см. (1)),… … Большая политехническая энциклопедия

поле — 3.12 поле: Установленное пространство для размещения конкретного элемента данных в составе зоны. Источник: ГОСТ Р 52535.1 2006: Карты идентификационные. Машиносчитываемые дорожные документы. Часть 1. Машиносчитываемые паспорта … Словарь-справочник терминов нормативно-технической документации

Вращающееся поле — Circular field Вращающееся поле. Магнитное поле, которое (а) окружает немагнитный проводник электричества, (в) полностью содержится в пределах магнитного проводника электричества или (с) существует внутри и окружает магнитный проводник. Обычно… … Словарь металлургических терминов

Источник

Вращающееся магнитное поле

Вы будете перенаправлены на Автор24

В 1824 г. французский ученый. Д.Ф Араго открыл явление, которое назвали «магнетизмом вращения». Оно заключалось в том, что при вращении магнитной стрелки (магнита), медный диск, подвешенный на оси над стрелкой (или находящийся под ней) начинал вращаться.

Это явление объяснил М. Фарадей тем, что вращающееся магнитное поле порождает в диске вихревые токи, и эти токи взаимодействуют с магнитом.

Вращающимся магнитным полем называют магнитное поле, которое характеризуется вектором магнитной индукции постоянным по величине, но изменяющим свое направление, а именно вращающимся с неизменной угловой скоростью.

Иногда вращающимися считают магнитные поля, которые создают постоянные магниты, совершающие вращательные движения относительно оси, которая не совпадает с осью их симметрии.

Вращающееся магнитное поле можно получить, если наложить два и более магнитных поля:

Вращающееся магнитное поле может быть получено в многофазных системах. При этом используются неподвижные катушки. Допустим, что магнитное поле в катушке создает синусоидальный электрический ток. Для того, чтобы система катушек с током создавала круговое вращающееся магнитное поле необходимо:

Система Тесла для получения вращающегося магнитного поля

Одним из первых вращающееся магнитное поле было получено Н. Тесла. Ученый использовал двухфазную систему. Он пропускал через две катушки (рис.1), расположенные под углом в 90° переменные электрические токи, изменяющиеся по гармоническим законам. При этом каждая катушка создавала пульсирующее магнитное поле.

Готовые работы на аналогичную тему

Рисунок 1. Система Тесла для получения вращающегося магнитного пол. Автор24 — интернет-биржа студенческих работ

В проекциях на оси декартовой системы координат ($XOY$) рис.1 уравнения (1) и (2) дают:

Найдем величину полученного поля по теореме Пифагора:

$tg\, \left( \alpha \right)=\frac>>=\frac\sin \left( \omega t \right)>\cos <(\omega t)>>=tg\left( \omega t \right)\to \alpha =\omega t\left( 6 \right)$

Эллиптическое магнитное поле

Если возникает асимметрия токов, порождающих магнитное поле или магнитных свойств сердечников катушек, то появляется асимметрия магнитного поля. При этом годограф вектора магнитной индукции покажет эллипс. Эллиптический годограф отвечает сумме пары векторов, имеющих круговые годографы, совершающих вращения в противоположных направлениях.

При совпадении прямого и обратного вращения, годограф вектора магнитной индукции выродится в прямую линию. При этом полученное поле называют пульсирующим.

Круговое магнитное поле можно считать частным случаем эллиптического. Такое становится возможным, если отсутствует одна из фаз.

Применение вращающегося магнитного поля

Взаимодействие вращающегося магнитного поля и электрического тока лежит в основании действия асинхронного двигателя. При этом электрический ток течет в обмотке ротора, вращающееся магнитное поле создается обмотками статора.

Статор имеет трехфазную обмотку. Ее оси сдвинуты в пространстве на 120° по окружности. В обмотках статора текут токи, изменяющиеся в соответствии с законами:

Переменные токи порождают магнитные поля с индукциями, направленными по осям обмоток:

По принципу суперпозиции результирующее поле в сердечнике статора получается, как сумма отдельных полей. Используя векторную диаграмму сложения:

и подход с проектированием на оси (XYZ) декартовой системы координат (как выше в двухфазной системе), величину результирующего поля имеем:

При этом вектор магнитной индукции образует с осью ординат угол, равный:

$tg\, \left( \hat<\vec\vec> \right)=tg\, \left( \omega t \right)\to\alpha =\omega t\left( 10 \right)$

Мы получили, что постоянный по величине вектор магнитной индукции вращается с неизменной угловой скоростью ω, то есть имеем вращающееся по кругу магнитное поле.

Направление вращения магнитного поля определено очередностью фаз. Если переключить любые две обмотки, то поле станет вращаться в противоположную сторону.

При увеличении количества пазов сердечника, и делении каждой обмотки надвое (причем ее пазы следует разместить так, что начала и концы частей обмоток находятся в пазах, которые смещены по окружности статора на π/2), то при включении сети возникнет магнитное поле с удвоенным количеством полюсов. Частота такого поля станет вдвое меньше.

Чаще всего частоту вращения магнитного поля называют скоростью вращения ($n$). Единицей вращения этой скорости считают оборот в минуту.

Каждая фазная обмотка отдельно создает пульсирующее поле. Пульсирующее поле появляется при авариях, например, обрыве какой – то фазы.

Источник

Вращающееся магнитное поле это

Как было показано ранее, одним из важнейших преимуществ многофазных систем является получение вращающегося магнитного поля с помощью неподвижных катушек, на чем основана работа двигателей переменного тока. Рассмотрение этого вопроса начнем с анализа магнитного поля катушки с синусоидальным током.

Магнитное поле катушки с синусоидальным током

При пропускании по обмотке катушки синусоидального тока она создает

магнитное поле, вектор индукции которого изменяется (пульсирует) вдоль этой катушки также по синусоидальному закону Мгновенная ориентация вектора магнитной индукции в пространстве зависит от намотки катушки и мгновенного направления тока в ней и определяется по правилу правого буравчика. Так для случая, показанного на рис. 1, вектор магнитной индукции направлен по оси катушки вверх. Через полпериода, когда при том же модуле ток изменит свой знак на противоположный, вектор магнитной индукции при той же абсолютной величине поменяет свою ориентацию в пространстве на 1800. С учетом вышесказанного магнитное поле катушки с синусоидальным током называют пульсирующим.

Круговое вращающееся магнитное поле
двух- и трехфазной обмоток

Круговым вращающимся магнитным полем называется поле, вектор магнитной индукции которого, не изменяясь по модулю, вращается в пространстве с постоянной угловой частотой.

Для создания кругового вращающегося поля необходимо выполнение двух условий:

Рассмотрим получение кругового вращающегося магнитного поля в случае двухфазной системы Тесла (рис. 2,а).

При пропускании через катушки гармонических токов каждая из них в соответствии с вышесказанным будет создавать пульсирующее магнитное поле. Векторы и , характеризующие эти поля, направлены вдоль осей соответствующих катушек, а их амплитуды изменяются также по гармоническому закону. Если ток в катушке В отстает от тока в катушке А на 90 0 (см. рис. 2,б), то .

Найдем проекции результирующего вектора магнитной индукции на оси x и y декартовой системы координат, связанной с осями катушек:

Модуль результирующего вектора магнитной индукции в соответствии с рис. 2,в равен

,

(1)

,

.

(2)

Полученные соотношения (1) и (2) показывают, что вектор результирующего магнитного поля неизменен по модулю и вращается в пространстве с постоянной угловой частотой , описывая окружность, что соответствует круговому вращающемуся полю.

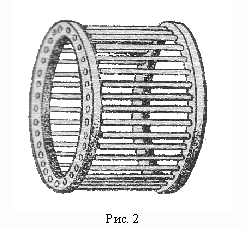
Покажем, что симметричная трехфазная система катушек (см. рис. 3,а) также позволяет получить круговое вращающееся магнитное поле.

Каждая из катушек А, В и С при пропускании по ним гармонических токов создает пульсирующее магнитное поле. Векторная диаграмма в пространстве для этих полей представлена на рис. 3,б. Для проекций результирующего вектора магнитной индукции на

оси декартовой системы координат, ось y у которой совмещена с магнитной осью фазы А, можно записать

;

(3)

.

(4)

Приведенные соотношения учитывают пространственное расположение катушек, но они также питаются трехфазной системой токов с временным сдвигом по фазе на 1200. Поэтому для мгновенных значений индукций катушек имеют место соотношения

; ; .

Подставив эти выражения в (3) и (4), получим:

;

(5)

(6)

В соответствии с (5) и (6) и рис. 2,в для модуля вектора магнитной индукции результирующего поля трех катушек с током можно записать:

,

,

.

Таким образом, и в данном случае имеет место неизменный по модулю вектор магнитной индукции, вращающийся в пространстве с постоянной угловой частотой , что соответствует круговому полю.

Магнитное поле в электрической машине

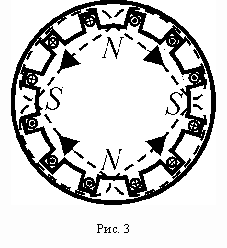
С целью усиления и концентрации магнитного поля в электрической машине для него создается магнитная цепь. Электрическая машина состоит из двух основных частей (см. рис. 4): неподвижного статора и вращающегося ротора, выполненных соответственно в виде полого и сплошного цилиндров.

На статоре расположены три одинаковые обмотки, магнитные оси которых сдвинуты по расточке магнитопровода на 2/3 полюсного деления , величина которого определяется выражением

,

На рис. 4 сплошными линиями (А, В и С) отмечены положительные направления пульсирующих магнитных полей вдоль осей обмоток А, В и С.

Приняв магнитную проницаемость стали бесконечно большой, построим кривую распределения магнитной индукции в воздушном зазоре машины, создаваемой обмоткой фазы А, для некоторого момента времени t (рис. 5). При построении учтем, что кривая изменяется скачком в местах расположения катушечных сторон, а на участках, лишенных тока, имеют место горизонтальные участки.

Заменим данную кривую синусоидой (следует указать, что у реальных машин за счет соответствующего исполнения фазных обмоток для результирующего поля такая замена связана с весьма малыми погрешностями). Приняв амплитуду этой синусоиды для выбранного момента времени t равной ВА, запишем

(7)

;

(8)

.

(9)

С учетом гармонически изменяющихся фазных токов для мгновенных значений этих величин при сделанном ранее допущении о линейности зависимости индукции от тока можно записать

.

Подставив последние соотношения в (7)…(9), получим

;

(10)

;

(11)

.

(12)

Просуммировав соотношения (10)…(12), с учетом того, что сумма последних членов в их правых частях тождественно равна нулю, получим для результирующего поля вдоль воздушного зазора машины выражение

,

представляющее собой уравнение бегущей волны.

Магнитная индукция постоянна, если . Таким образом, если мысленно выбрать в воздушном зазоре некоторую точку и перемещать ее вдоль расточки магнитопровода со скоростью

,

то магнитная индукция для этой точки будет оставаться неизменной. Это означает, что с течением времени кривая распределения магнитной индукции, не меняя своей формы, перемещается вдоль окружности статора. Следовательно, результирующее магнитное поле вращается с постоянной скоростью. Эту скорость принято определять в оборотах в минуту:

.

Принцип действия асинхронного и синхронного двигателей

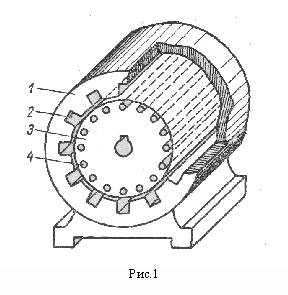
Устройство асинхронного двигателя соответствует изображению на рис. 4. Вращающееся магнитное поле, создаваемое расположенными на статоре обмотками с током, взаимодействует с токами ротора, приводя его во вращение. Наибольшее распространение в настоящее время получил асинхронный двигатель с короткозамкнутым ротором ввиду своей простоты и надежности. В пазах ротора такой машины размещены токонесущие медные или алюминиевые стержни. Концы всех стержней с обоих торцов ротора соединены медными или алюминиевыми же кольцами, которые замыкают стержни накоротко. Отсюда и произошло такое название ротора.

называется относительным скольжением. Для двигателей нормального исполнения S=0,02…0,07. Неравенство скоростей магнитного поля и ротора становится очевидным, если учесть, что при вращающееся магнитное поле не будет пересекать токопроводящих стержней ротора и, следовательно, в них не будут наводиться токи, участвующие в создании вращающегося момента.

Принципиальное отличие синхронного двигателя от асинхронного заключается в исполнении ротора. Последний у синхронного двигателя представляет собой магнит, выполненный (при относительно небольших мощностях) на базе постоянного магнита или на основе электромагнита. Поскольку разноименные полюсы магнитов притягиваются, то вращающееся магнитное поле статора, которое можно интерпретировать как вращающийся магнит, увлекает за собой магнитный ротор, причем их скорости равны. Это объясняет название двигателя – синхронный.

В заключение отметим, что в отличие от асинхронного двигателя, у которого обычно не превышает 0,8…0,85, у синхронного двигателя можно добиться большего значения и сделать даже так, что ток будет опережать напряжение по фазе. В этом случае, подобно конденсаторным батареям, синхронная машина используется для повышения коэффициента мощности.

Источник

Вращающееся магнитное поле

Магнитное поле, ось которого вращается в пространстве с постоянной угловой частотой, называется вращающимся магнитным полем. Если при этом величина индукции в любой точке оси магнитного поля остается постоянной, то такое поле называется круговым вращающимся магнитным полем. Это связано с тем, что его можно изобразить вращающимся в пространстве вектором постоянной длины, конец которого при вращении описывает окружность.

Если схематически представить обмотки статора состоящими из одного витка, то на статоре будет только шесть пазов, в каждом из которых будет лежать половина витка обмотки. Обозначим начала витков обмоток буквами A, B и C, а концы витков буквами X, Y и Z. Обозначим также направления протекания тока в витках обмоток, считая положительным направление от начала к концу обмотки. Тогда для положительных значений тока стороны A, B и C будут обозначены крестом, а стороны X, Y и Z – точкой( рис.2).

Направление вращения магнитного поля определяется последовательностью подключения обмоток к трехфазной сети. Для изменения направления вращения достаточно поменять местами точки подключения двух любых обмоток.

Основные понятия и принцип действия асинхронной машины

Конструктивная схема асинхронной машины показана на рисунке 1. Она состоит из пакета статора 1 с пазами 2 для укладки обмотки и цилиндрического ротора 3 в круглых пазах которого находятся проводники (стержни) 4 его обмотки. Стержни замкнуты по краям кольцами (на рисунке не показаны), поэтому обмотка ротора называется короткозамкнутой. Такой тип ротора наиболее распространен у асинхронных машин, т.к. он прост, надежен и технологичен. Если мысленно извлечь обмотку ротора из пакета ротора, то она будет иметь вид, показанный на рисунке 2. Этот тип обмотки называется «беличья клетка».

Кроме роторов типа «беличья клетка» в асинхронных машинах применяются ротора, у которых в пазах уложена такая же трехфазная обмотка (рис 3 1), как в статоре. Для подключения к внешним электрическим цепям (5) концы обмотки выведены наружу через контактные кольца (3) и щетки (4)(см. рисунок). Такой тип ротора называется фазным

Обмотка ротора не имеет электрического соединения с внешними цепями и ток в ней возникает в результате электромагнитной индукции. Этот процесс происходит следующим образом. Трехфазная обмотка статора подключается к сети переменного тока и ток обмотки ( ) формирует круговое вращающееся магнитное поле. Поле статора ( ) вращается в пространстве относительно оси вращения ротора ( ) и пересекает стержни его обмотки. В результате в них наводится ЭДС индукции ( ) и т.к. концы стержней ротора электрически замкнуты кольцами, то в них под действием ЭДС формируется электрический ток ( ). Взаимодействие протекающего в стержнях тока с внешним магнитным полем вызывает действие силы (F) и соответствующего электромагнитного момента (M), приводящего ротор во вращение ( ). Таким образом, возникновение вращающего момента возможно только в случае, если стержни ротора пересекают магнитное поле статора, а для этого необходимо, чтобы ротор вращался со скоростью отличной от скорости вращения магнитного поля, т.е. чтобы он вращался несинхроннно с полем. Отсюда происходит название этой машины – асинхронная.

Сказанное выше можно представить в виде логической последовательности , в которой существует только один условный переход от вращающегося поля к ЭДС и току ротора. Если , то поле и ротор вращаются синхронно и ЭДС ротора не возбуждается. Такой режим называется холостым ходом и он может создаваться только за счет внешнего вращающего момента.

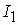
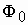
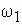
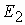
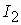
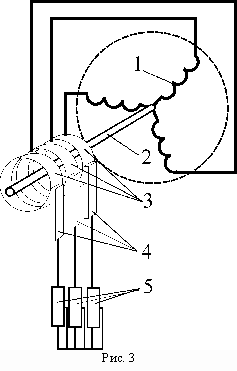
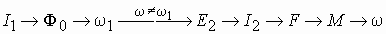
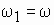
Если скорость вращения ротора меньше скорости вращения поля, то электромагнитный момент действующий на ротор положительный и стремится разогнать его. При скорости ротора выше скорости поля направления ЭДС и тока в роторе меняются на противоположные. Электромагнитный момент также меняет знак и становится тормозящим.

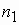
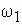
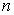
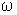
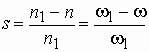
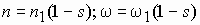
Для описания электромеханических процессов в асинхронной машине обычно пользуются понятием скольжения s. Оно равно разности скоростей или частот вращения магнитного поля ( )и ротора ( ) отнесенной к скорости или частоте вращения магнитного поля . Отсюда скорость или частоту вращения можно выразить через скольжение . Скорость или частоту вращения магнитного поля называют также синхронной скоростью или частотой.

Основной магнитный поток и потоки рассеяния. Индуктивные сопротивления

В обмотке ротора протекают токи, наводимые ЭДС индукции. Они формируют собственное поле ротора вращающееся относительно тела ротора с частотой скольжения . Таким образом, поле ротора участвует в двух вращательных движениях – движении относительно тела тора и вместе с ним относительно статора с частотой . Следовательно, частота вращения поля ротора равна , т.е. поле ротора вращается в пространстве с такой же частотой, что и поле статора. Поэтому эти поля неподвижны друг относительно друга и образуют единое поле машины. Основная часть магнитного потока поля охватывает обмотки статора и ротора, пересекая воздушный зазор . Эта часть называется основным магнитным потоком Ф. Две другие части сцепляются только с одной из обмоток и образуют соответствующие потоки рассеяния и . Потоки рассеяния формируют в обмотках ЭДС рассеяния или ЭДС самоиндукции, которые можно представить через токи обмоток и соответствующие индуктивности рассеяния с учетом того, что токи в обмотках статора и ротора имеют разную частоту ( и ): и , где и – индуктивные сопротивления рассеяния при частоте статора.

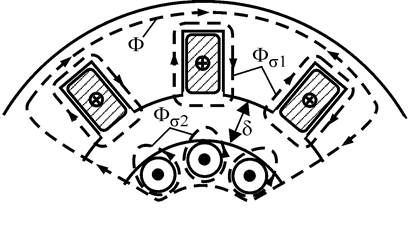
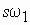
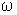
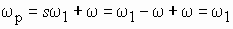
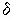
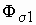
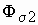
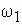
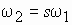
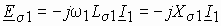
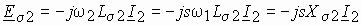
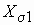
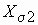
Электродвижущие силы обмоток

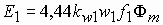
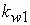
Вращающееся магнитное поле пересекает витки обмотки статора и наводит в них ЭДС. По аналогии с трансформатором можно написать , где – обмоточный коэффициент, учитывающий конструктивные особенности обмотки статора (укорочение шага, распределение обмотки по пазам, скос пазов). В трансформаторах картина магнитного поля более простая, т.к. основной магнитный поток охватывает практически все витки обмотки и введение обмоточного коэффициента не требуется.

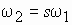
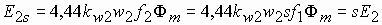
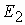
Обмотка ротора пересекается основным магнитным потоком с частотой . Отсюда ЭДС обмотки – , где – ЭДС обмотки ротора при частоте статора , т.е. при неподвижном роторе.

Магнитодвижущие силы и токи статора и ротора

Оптимальное преобразование энергии в асинхронной машине возможно при условии, что магнитодвижущие силы (МДС) обмоток распределены вдоль окружности зазора по синусоидальному закону. Однако обмотки статора представляют собой катушки, создающие МДС с распределением близким к прямоугольному. Поэтому их разделяют на секции и раскладывают вдоль зазора в соседние пазы. 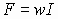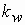В результате МДС приобретает распределение близкое к синусоидальному, но если выделить основную пространственную гармонику, которая собственно и требуется для работы машины, то окажется, что расчет МДС по выражению справедливому для сосредоточенной обмотки , где w и I – число витков и ток в обмотке, окажется завышенным. Поэтому для расчета МДС асинхронной машины вводят т.н. обмоточный коэффициент , учитывающий конструктивные особенности обмоток – распределение вдоль зазора, скос пазов и укорочение шага. В результате введения этого коэффициента реальная распределенная обмотка как бы преобразуется в сосредоточенную обмотку, которая при токе равном току в реальной обмотке создает МДС с синусоидальным распределением, соответствующим МДС основной гармонике реальной обмотки.

С учетом сказанного полные МДС, создаваемые всеми обмотками статора и ротора, можно представить в виде

, где — число фаз; — число витков; — обмоточные коэфициенты соответственно статора и ротора.

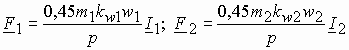
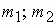
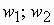
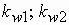
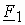
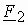
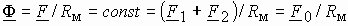
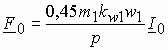
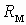
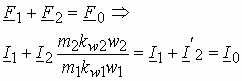
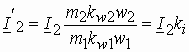
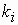
Основной магнитный поток машины создается совместным действие МДМ обмоток статора и ротора . Также как в трансформаторе этот поток не зависит от нагрузки машины и определяется только напряжением питающей сети, т.е. , где – МДС статора в режиме холостого хода, а – магнитное сопротивление машины. Отсюда

, где – ток статора, приведенный к параметрам обмотки ротора, а – коэффициент трансформации токов асинхронной машины.

Следует заметить, что число фаз обмотки ротора типа «беличья клетка» равно числу стержней, а число витков 0,5.

Дата добавления: 2016-06-29 ; просмотров: 8130 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник