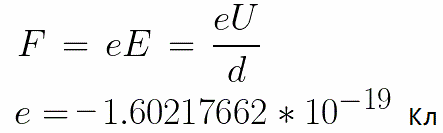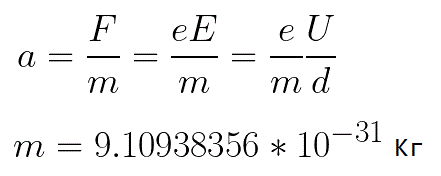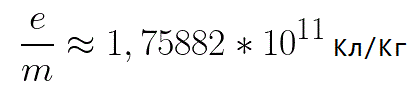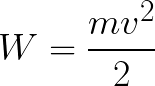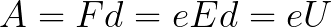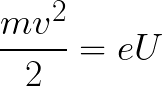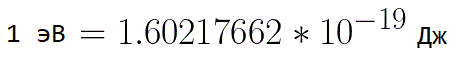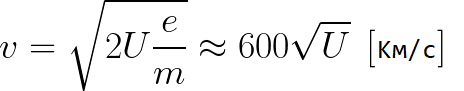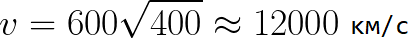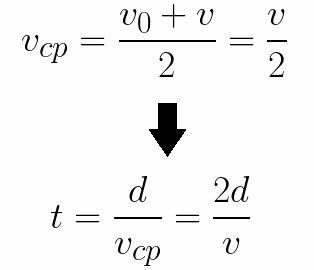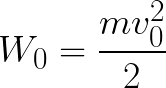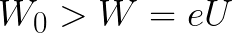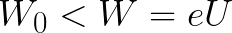Электрон в электрическом поле

Движение электрона в электрическом поле является одним из важнейших для электротехники физических процессов. Разберемся как это происходит в вакууме. Сначала рассмотрим пример движения электрона от катода к аноду в однородном электрическом поле.

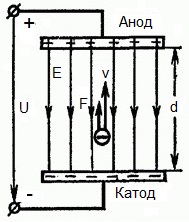
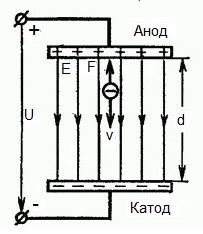
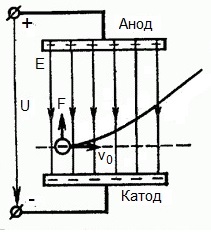
На приведенном ниже рисунке изображена ситуация, когда электрон покидает отрицательный электрод (катод) с пренебрежимо малой начальной скоростью (стремящейся к нулю), и попадает в однородное электрическое поле, присутствующее между двумя электродами.

К электродам приложено постоянное напряжение U, а электрическое поле обладает соответствующей напряженностью E. Расстояние между электродами равно d. В данном случае на электрон со стороны поля будет действовать сила F, пропорциональная заряду электрона и напряженности поля:

Поскольку электрон обладает отрицательным зарядом, то эта сила будет направлена против вектора E напряженности поля. Соответственно электрон будет в данном направлении электрическим полем ускоряться.

Ускорение a, которое испытывает электрон, пропорционально величине действующей на него силы F и обратно пропорционально массе электрона m. Поскольку поле однородно, ускорение для данной картины можно выразить так:

В этой формуле отношение заряда электрона к его массе есть удельный заряд электрона — величина, являющаяся физической константой:

Итак, электрон находится в ускоряющем электрическом поле, ибо направление начальной скорости v0 совпадает с направлением силы F со стороны поля, и электрон движется поэтому равноускоренно. Если никаких препятствий нет, то он пройдет путь d между электродами и попадет на анод (положительный электрод) с некой скоростью v. В момент когда электрон достигнет анода, его кинетическая энергия будет соответственно равна:

Поскольку на всем пути d электрон ускорялся силами электрического поля, то данную кинетическую энергию он приобрел в результате работы, которую совершила сила, действующая со стороны поля. Эта работа равна:

Тогда кинетическая энергия, которую приобрел электрон двигаясь в поле, может быть найдена следующим образом:

То есть это есть ни что иное, как работа сил поля по ускорению электрона между точками с разностью потенциалов U.

В подобных ситуациях для выражения энергии электрона удобно использовать такую единицу измерения как «электронвольт», равную энергии электрона при напряжении в 1 вольт. А поскольку заряд электрона является константой, то и 1 электронвольт — также постоянная величина:

Из предыдущей формулы можно легко определить скорость электрона в любой точке на его пути при движении в ускоряющем электрическом поле, зная лишь разность потенциалов которую он прошел ускоряясь:

Как мы видим, скорость электрона в ускоряющем поле зависит лишь от разности потенциалов U между конечной и стартовой точками его пути.

Представим, что электрон начал движение от катода с пренебрежимо малой скоростью, а напряжение между катодом и анодом равно 400 вольт. В этом случае в момент достижения анода его скорость будет равна:

Тут же легко можно определить время, за которое электрон пройдет расстояние d между электродами. При равноускоренном движении из состояния покоя средняя скорость находится как половина конечной скорости, тогда время ускоренного полета в электрическом поле будет равно:

Предположим что электрон покинул анод с какой-то начальной скоростью v и изначально стал двигаться в направлении катода. В этом случае сила F, действующая на электрон со стороны электрического поля, будет направлена против вектора электрической напряженности Е — от катода к аноду.

Она станет уменьшать начальную скорость электрона, то есть поле будет замедлять электрон. Значит электрон в данных условиях станет двигаться равномерно равнозамедленно. Ситуация описывается так: «электрон движется в тормозящем электрическом поле».

От анода электрон начал двигаться с отличной от нуля кинетической энергией, которая при торможении начинает уменьшаться, поскольку энергия теперь расходуется на преодоление силы, действующей со стороны поля навстречу электрону.

Если начальная кинетическая энергия электрона, когда он покинул анод, сразу была больше энергии, которую необходимо затратить полю на ускорение электрона при движении от катода к аноду (как в первом примере), то электрон пройдет расстояние d и в итоге все же достигнет катода несмотря на торможение.

А что если электрон влетает на скорости v0 в область действия электрического поля под прямым углом? Очевидно, сила со стороны поля в этой области направлена для электрона от катода к аноду, то есть против вектора напряженности электрического поля E.

Значит электрон теперь имеет две составляющие движения: первая — со скоростью v0 перпендикулярно полю, вторая — равноускоренно под действием силы со стороны поля, направленной к аноду.

Получается, что влетев в область действия поля, электрон движется по параболической траектории. Но вылетев за пределы области действия поля, электрон продолжит равномерное движение по инерции по прямолинейной траектории.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Julia и движение заряженной частицы в электромагнитном поле

Закрепляем навыки решения и визуализации дифференциальных уравнений на примере одного из самых распространенных эволюционных уравнений, вспоминаем о старом-добром Scilab и пытаемся понять, а надо ли оно нам… Под катом картинки (килобайт на семьсот)

и приступим к постановке задачи

Движение заряженных частиц в электромагнитном поле

На заряженую частицу с зарядом движущуюся в ЭМП со скоростью действует сила Лоренца: . Данная формула справедлива при ряде упрощений. Пренебрегая поправками на теорию относительности, считаем массу частицы постоянной, так что уравнение движения имеет вид:

Направим ось Y вдоль электрического поля, ось Z — вдоль магнитного поля и предположим для простоты, что начальная скорость частицы лежит в плоскости XY. В этом случае вся траектория частицы также будет лежать в этой плоскости. Уравнения движения примут вид:

Обезразмерим: . Звёздочками обозначены размерные величины, а — характерный размер рассматриваемой физической системы. Получим безразмерную систему уравнений движения заряженной частицы в магнитном поле:

В качестве начальной конфигурации модели выберем: Тл, В/м, м/с. Для численного решения воспользуемся пакетом DifferentialEquations:

Здесь используется метод Эйлера, для которого задаётся количество шагов. Также сохраняется в матрицу ответов не всё решение системы, а только 1 и 2 индексы, то есть координаты икс и игрек (скорости нам не нужны).

Проверим результат. Введем вместо х новую переменную . Таким образом осуществляется переход в новую систему координат, движущуюся относительно исходной со скоростью u в направлении оси Х:

Если выбрать и обозначить , то система упростится:

Электрическое поле исчезло из последних равенств, и они представляют собой уравнения движения частицы, находящейся под действием однородного магнитного поля. Таким образом, частица в новой системе координат (х, у) должна двигаться по окружности. Так как эта новая система координат сама перемещается относительно исходной со скоростью , то результирующее движение частицы будет складываться из равномерного движения по оси X и вращения по окружности в плоскости XY. Как известно, траектория, возникающая при сложении таких двух движений, в общем случае представляет собой трохоиду. В частности, если начальная скорость равна нулю, реализуется простейший случай движения такого рода — по циклоиде.
Удостоверимся, что скорость дрейфа вышла действительно равной Е/В. Для этого:

Out: 8.333333333333332e-5
С точностью до седьмого порядка!
Для удобства определим функцию, принимающую параметры модели и подпись графика, которая будет также служить названием файла png, создаваемого в папке с проектом (работает в Juno/Atom и Jupyter). В отличии от Gadfly, где графики создавались в слоях, а потом выводились функцией plot(), в Plots, чтобы в одном фрейме наделать разных графиков, первый из них создается функцией plot(), а последующие добавляются использованием plot!(). Названия функций меняющих принимаемые объекты в Джулии принято оканчивать восклицательным знаком.

При нулевой начальной скорости, как и предполагалось, получаем циклоиду:

Получим траекторию частицы при занулении индукции, напряженности и при смене знака заряда. Напомню, что точка значит поочередное выполнение функции со всеми элементами массива

Немного о Scilab

На Хабре уже есть достаточно информации о Сайлабе, например 1, 2, а тут про Octave поэтому ограничимся ссылками на Википедию и на домашнюю страницу.

От себя добавлю, про наличие удобного создания интерфейса с флажками кнопками и выводом графиков и довольно интересного инструмента визуального моделирования Xcos. Последний можно использовать, например, для моделирования сигнала в электротехнике:

И здесь очень удобное руководство:

Собственно, нашу задачу вполне можно решить и в Scilab:

Здесь информация по функции для решения дифуров ode. В принципе напрашивается вопрос

А зачем нам Julia?

… если и так есть такие замечательные штуки как Scilab, Octave и Numpy, Scipy?
Про последние два не скажу — не пробовал. Да и вообще вопрос сложный, так что прикинем навскидку:

Scilab
На харде займет чуть больше 500 Мб, запускается быстро и сходу доступно и дифуросчитание, и графика и всё остальное. Хорош для начинающих: отличное руководство (по большей части локализованное), есть много книг на русском. Про внутренние ошибки уже было сказано тут и здесь, и так как продукт очень нишевый, сообщество вялое, и дополнительные модули весьма скудны.

Julia
По мере добавления пакетов (особенно всякой питонщины а-ля Jupyter и Mathplotlib) разрастается от 376 Мб до вполне-таки шести с лишним гигабайт. Оперативку она тоже не щадит: на старте 132 Мб и после того, как в Юпитере намалевать графиков, до 1 ГБ спокойно дойдёт. Если работать в Juno, то всё почти как в Scilab: можно выполнять код сразу в интерпретаторе, можно печатать во встроенном блокноте и сохранять как файл, есть обозреватель переменных, журнал команд и интерактивная справка. Лично у меня вызывает возмущение отсутствие clear(), т. е. запустил я код, потом начал там поправлять и переименовывать, а старые переменные-то остались (в Юпитере нет обозревателя переменных).

Но всё это не критично. Scilab подходит вполне на первых парах, сделать лабу, курсач или посчитать чего промежуточного — очень даже подручный инструмент. Хоть здесь тоже есть поддержка параллельного вычисления и вызов сишных/фортрановских функций, для чего серьезного его использовать не получается. Большие массивы повергают его в ужас, чтоб задать многомерные, приходится заниматься всяким мракобесием, а вычисления за рамками классических задач вполне могут обронить всё вместе с операционкой.

И вот после всех этих болей и разочарований можно смело переходить на Julia, чтоб огрести ещё и здесь. Будем учиться дальше, благо комьюнити очень отзывчивое, проблемы утрясаются быстро, да и у Джулии есть еще много интересных особенностей, которые превратят процесс обучения в увлекательное путешествие!

Источник

Движение электронов в электрическом и магнитном полях

Управление движением свободных электронов в большинстве электронных приборов осуществляется с помощью электрических или магнитных полей. В чем состоит сущность этих явлений?

Электрон в электрическом поле. Взаимодействие движущихся электронов с электрическим полем – основной процесс, происходящий в большинстве электронных приборов.

Наиболее простым случаем является движение электрона в однородном электрическом поле, т.е. в поле, напряженность которого одинакова в любой точке, как по величине, так и по направлению. На рисунке показано однородное электрическое поле, созданное между двумя параллельными пластинами достаточно большой протяженности, чтобы пренебречь искривлением поля у краев. На электрон, как и на любой заряд, помещенный в электрическое поле с напряженностью Е, действует сила, равная произведению величины заряда на напряженность поля в месте нахождения заряда,

Знак минус показывает, что вследствие отрицательного заряда электрона сила имеет направление, противоположное направлению вектора напряженности электрического поля. Под действием силы F электрон двигается навстречу электрическому полю, т.е. перемещается в сторону точек с более высоким потенциалом. Поэтому поле в данном случае является ускоряющим.

Работа, затраченная электрическим полем на перемещение заряда из одной точки в другую, равна произведению величины заряда на разность потенциалов между этими точками, т.е. для электрона

где U— разность потенциалов между точками 1 и 2. Эта работа затрачивается на сообщение электрону кинетической энергии

Если начальная скорость электрона V₀ = 0, то

Отсюда можно определить скорость электрона в электрическом поле при разности потенциалов U:

Таким образом, скорость, приобретенная электроном при движении в ускоряющем поле, зависит только от пройденной разности потенциалов. Из формулы (1.17) видно, что скорости электронов, даже при сравнительно небольшой разности потенциалов, получаются значительными. Например, при U = 100 В получаем V = 6000 км/с. При такой большой скорости электронов все процессы в приборах, связанные с движением электронов, протекают очень быстро. Например, время, необходимое для пролета электронов между электродами в электронной лампе, составляет доли микросекунды. Именно поэтому работа большинства электронных приборов может считаться практически безинерционной.

Рассмотрим теперь движение электрона, у которого начальная скорость Vo направлена против силы F, действующей на электрон со стороны поля (Рис. 1.8, б). В этом случае электрическое поле является для электрона тормозящим. Скорость движения электрона и его кинетическая энергия в тормозящем поле уменьшаются, так как в данном случае работа совершается не силами поля, а самим электроном, который за счет своей энергии преодолевает сопротивление сил поля. Энергия, теряемая электроном, переходит к полю. Действительно, поскольку движение электрона в тормозящем поле означает его перемещение в направлении отрицательного полюса источника поля, то при приближении электрона к последнему суммарный отрицательный заряд увеличивается и соответственно увеличивается энергия поля. В тот момент, когда электрон полностью израсходует свою кинетическую энергию, его скорость окажется равной нулю, и затем электрон начнет движение в обратном направлении. Движение его в обратном направлении является не чем иным, как рассмотренным выше движением без начальной скорости в ускоряющем поле. При таком движении электрона поле возвращает ему ту энергию, которую он потерял при своем замедленном движении.

В рассмотренных выше случаях направление скорости движения электрона было параллельным направлению электрических силовых линий поля. Такое электрическое поле называется продольным.Поле, направленное перпендикулярно вектору начальной скорости электрона, называется поперечным.

Рассмотрим вариант, когда электрон влетает в электрическое поле с некоторой начальной скоростью Vo и под прямым углом к направлению электрических силовых линий (рис. 1.8, в). Поле действует на электрон с постоянной силой, определяемой по формуле (1.11) и направленной в сторону более высокого положительного потенциала. Под действием этой силы электрон приобретает скорость V₁, направленную навстречу полю. В результате электрон совершает одновременно два взаимно перпендикулярных движения: прямолинейное равномерное по инерции со скоростью V₀ и прямолинейно

равномерно ускоренное со скоростью V₁. Под влиянием этих двух взаимно перпендикулярных скоростей электрон будет двигаться по траектории, представляющей собой параболу. После выхода из электрического поля электрон будет двигаться по инерции прямолинейно.

Электрон в магнитном поле.Влияние магнитного поля на движущийся электрон можно рассматривать как действие этого поля как на проводник с током. Движение электрона с зарядом е и скоростью V эквивалентно току i, проходящему через элементарный отрезок проводника длиной Δl.

Согласно основным законам электромагнетизма сила, действующая в магнитном поле на провод длиной Δl с током i равна

где В- магнитная индукция; α–угол между направлением тока и магнитной силовой линией поля.

Используя соотношение (1.18), получим новое выражение, характеризующее силу воздействия магнитного поля на движущийся в нем электрон,

Из этого выражения видно, что электрон, движущийся вдоль силовых линий магнитного поля (α = 0), не испытывает никакого воздействия поля (F = BeVsin0=0)и продолжает перемещаться с заданной ему скоростью.

Если вектор начальной скорости электрона перпендикулярен вектору магнитной индукции, т.е. α = 90, то сила, действующая на электрон,

Направление этой силы определяется по правилу левой руки. Сила F всегда перпендикулярна направлению мгновенной скорости V электрона и направлению магнитных силовых линий поля. В соответствии со вторым законом Ньютона эта сила сообщает электрону с массой m_e ускорение, равное . Поскольку ускорение перпендикулярно скорости V, то электрон под действием этого нормального (центростремительного) ускорения будет двигаться по окружности, лежащей в плоскости, перпендикулярной к силовым линия поля.

В общем случае начальная скорость электрона может быть неперпендикулярна к магнитной индукции. В данном случае траекторию движения электрона определяют две составляющие начальной скорости:

нормальная V₁ и касательная V₂, первая из которых направлена перпендикулярно силовым линиям магнитного поля, а вторая параллельно им. Под действием нормальной составляющей электрон движется по окружности, а под действие касательной – перемещается вдоль силовых линий поля рис. 1.9.

В результате одновременного действия обеих составляющих траектория движения электрона принимает вид спирали. Рассмотренная возможность изменения траектории движения электрона с помощью магнитного поля используется для фокусировки и управления электронным потоком в электронно-лучевых трубках и других приборах.

Источник