Что значит смежные вершины

Теория Графов. Часть 2 Смежность, инцидентность, петли

Ничего не сделано, если что-то осталось недоделанным. – Иоганн Гаусс

Смежность и инцидентность

Смежность и инцидентность

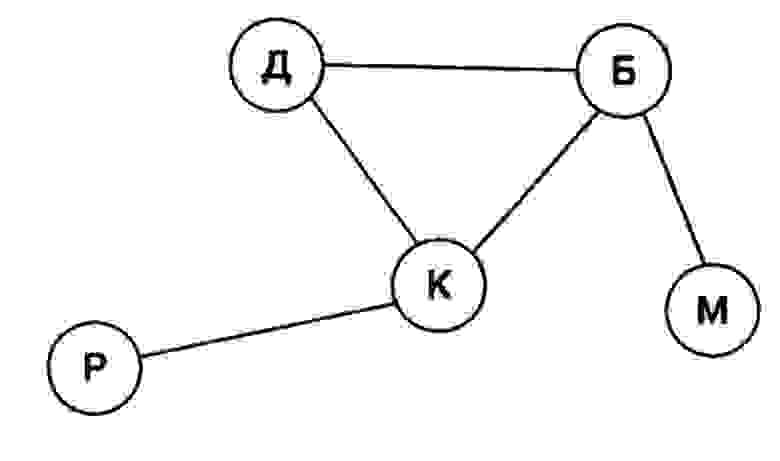
Давайте рассмотрим самый обыкновенный неориентированный граф (Рисунок 1). В нем есть вершина Р и вершина К. Данные вершины являются смежными (adjacent), так как они соединены ребром РК.

Помимо этого, как мы видим, вершина К является концом ребра РК, а Р его началом, в таких случаях вершина К и Р называются инцидентными (incident) ребру РК.

Рисунок 1

Смежностью вершин графа – называется отношение между двумя вершинами, в котором существует ребро их соединяющее.

Инцидентность – это когда вершина a является началом или концом ребра t. Если мы добавим еще одну вершину b, то мы скажем, что вершина a и b инцидента ребру t.

Кроме вершин, смежность присутствует и у рёбер. Рёбра просто должны иметь общую вершину. В нашем случаи мы можем сказать, что ребро ДК является смежным ребру РК, так как у них есть общая вершина К.

Смежностью рёбер графа – называется отношение между двумя рёбрами, в котором существует вершина соединяющая их.

В связи с тем, что выше мы рассматривали неориентированный граф, то было неважно, с какого направления определять смежность и инцидентность. Вершина Р могла быть смежна вершине К, но также мы могли сказать, что вершина К смежна вершине Р.

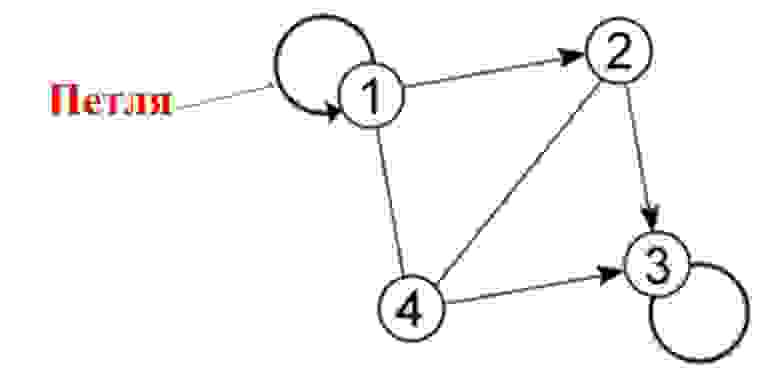
В ориентированном графе все немного по-другому (Рисунок 2), так у нас имеется направление, которое мы не в силах поменять. Если вершина 1 смежна вершине 2, то вершина 2 не может быть смежна вершине 1. То же самое касается и инцидентности. Вершины 1 и 2 инцидентны ребру 12, наоборот не работает.

Рисунок 2

Петли

Петля – это ребро инцидентное одной и той же вершине. То есть вершина которая соединена сама с собой. На рисунке ниже мы видим, как это выглядит.

Петли

Заключение

В следующей статье я покажу, как с помощью матрицы задавать графы, а также покажу, что такое вес ребра.

Источник

Многоугольник

Определение 1. Многоугольник − замкнутая ломаная линия.

Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:

Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.

Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.

Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.

Виды многоугольников

Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.

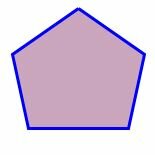На рисунке 1 представлены различные виды многоугольников.

Обозначение многоугольника

Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).

Соседние вершины многоугольника

Вершины многоугольника называются соседними, если они являются концами одной из его сторон.

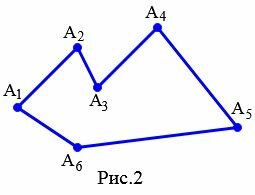На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)

Смежные стороны многоугольника

Стороны многоугольника называются смежными, если они имеют общую вершину.

На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)

Простой многоугольник. Самопересекающийся многоугольник

Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

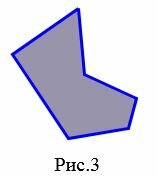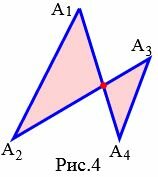На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.

Выпуклый многоугольник

Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

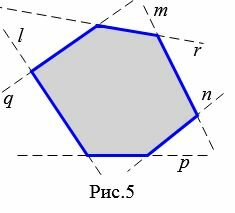На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.

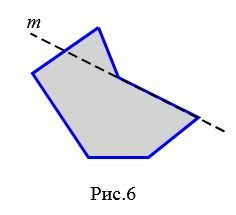На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.

Правильный многоугольник

Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.

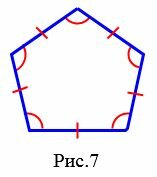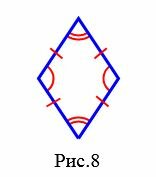На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Звездчатый многоугольник

Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.

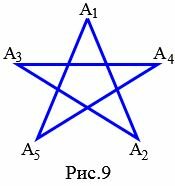На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)

Периметр многоугольника

Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_A_n \) периметр вычисляется из формулы:

Угол многоугольника

Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).

Внешний угол многоугольника

Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.

На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)

Диагональ многоугольника. Количество диагоналей

Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.

Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:

Сумма углов выпуклого многоугольника

Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_A_n \) (Рис.11):

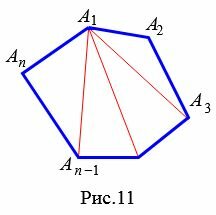Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)

где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.

Угол правильного многоугольника

Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:

где \( \small n \) −количество сторон (вершин) правильного многоугольника.

Источник

Ломаная

Определение 1. Ломаной (ломаной линией) \( \small A_1A_2. A_A_n \) называется геометрическая фигура, которая состоит из \( \small [ A_1A_2 ],\) \( \small [ A_2A_3 ]. \) \( \small [ A_A_n ]\) последовательно соединенных своими концами отрезков и никакие последовательные две отрезки\( \small [ A_A_ ]\) и \( \small [ A_A_ ]\) при \( \small k=1,2. n-2 \) не лежат на одной прямой.

Можно дать и другое определение ломаной:

Невырожденная ломаная

Ломаная, описанная в определении 1 называется невырожденной ломаной.

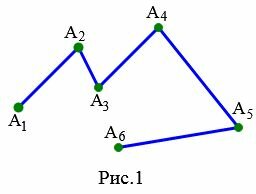
На рисунке 1 ломаная \( \small A_1A_2A_3A_4A_5A_6 \) является невырожденной поскольку отрезки \( \small [ A_1A_2 ]\) и \( \small [ A_2A_3 ]\), \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\), \( \small [ A_3A_4 ]\) и \( \small [ A_4A_5 ]\), \( \small [ A_4A_5 ]\) и \( \small [ A_5A_6 ]\) не лежат на одной прямой.

Вырожденная ломаная

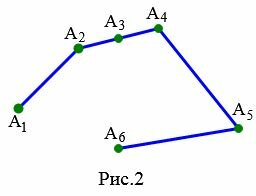На рисунке 2 изображена ломаная \( \small A_1A_2A_3A_4A_5A_6 \). Эта ломаная является вырожденной поскольку отрезки \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\) лежат на одной прямой.

Внимание! Если явно не указыается вырожденность ломаной, то подразумевается невырожденная ломаная.

Звенья ломаной

Звеньями называют отрезки, из которых состоит ломаная.

Вершины ломаной

Конечные точки звеньев ломаной называются вершинами.

На рисунке 1 изображена ломаная \( \small A_1A_2A_3A_4A_5A_6 \), состоящая из шести вершин: \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5, \ A_6 \).

Смежные звенья ломаной

Смежные звенья ломаной − это звенья имеющие общую вершину.

На рисунке 3 смежными звеньями ломаной \( \small A_1A_2A_3A_4A_5A_6 \) являются звенья: \( \small [ A_1A_2 ]\) и \( \small [ A_2A_3 ]\), \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\), \( \small [ A_3A_4 ]\) и \( \small [ A_4A_5 ]\), \( \small [ A_4A_5 ]\) и \( \small [ A_5A_6 ]\).

Смежные вершины ломаной

Смежными вершинами ломаной называют вершины одного звена ломаной.

На рисунке 3 смежными вершинами ломаной \( \small A_1A_2A_3A_4A_5A_6 \) являются вершины: \( \small A_1\) и \( \small A_2\), \( \small A_2\) и \( \small A_3\), \( \small A_3\) и \( \small A_4 \), \( \small A_4\) и \( \small A_5\), \( \small A_5\) и \( \small A_6\).

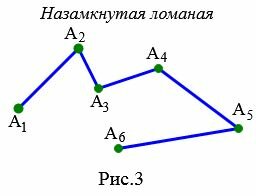
Незамкнутая ломанная

Незамкнутым является ломаная, первая и последняя точки которой не совпадают друг с другом (Рис.3).

Замкнутая ломанная

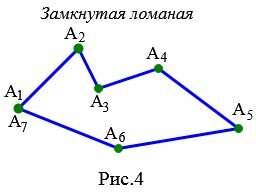На рисунке 4 ломаная \( \small A_1A_2A_3A_4A_5A_6A_7 \) является замкнутым, так как точки: \( \small A_1\) и \( \small A_7\) совпадают и отрезки \( \small A_1A_2\) и \( \small A_6A_7\) не лежат на одной прямой.

Ломаная с самопересечением

Ломаная имеет самопересечение, если хотя бы два ее звена имеют общую точку, помимо общей вершины.

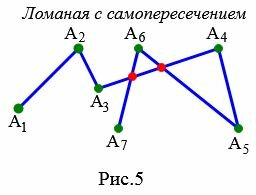Ни рисунке 5 ломаная \( \small A_1A_2A_3A_4A_5A_6A_7 \) имеет самопересечение, так как звенья \( \small A_5A_6 \) и \( \small A_6A_7 \) имеют общие точки со звеном \( \small A_3A_4 \).

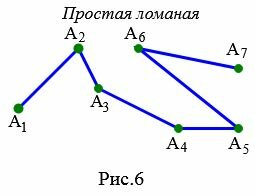
Простая ломаная

Ломаная называется простым, если не имеет самопересечений. Пример простой ломаной изображен на рисунке 6.

Длина ломаной

Длина ломаной равна сумме длин всех звеньев ломаной: \( \small d= A_1A_2+A_2A_3+. +A_A_n, \) где \( \small n \) − количество вершин ломаной.

Теорема. Длина ломаной больше расстояния между первым и последним точками.

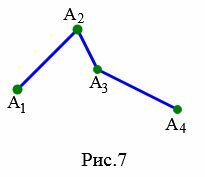Доказательство. Для доказательства теоремы рассмотрим ломаную \( \small A_1A_2A_3A_4 \) с тремя звеньями (Рис.7). Так как ломаная невырождена, то вершины \( \small A_1, \ A_2, \ A_3 \) не лежат на одной прямой. Тогда имеет место неравенство треугольников:

Для точек \( \small A_1, \ A_3, \ A_4 \) имеет место следующее нестрогое неравенство:

В выражении (2) мы не применяли строгое неравенство поскольку вершины \( \small A_1, \ A_3, \ A_4 \) ломаной не являются соседними вершинами и могут лежать на одной прямой.

В неравенстве (2) вместо слагаемого \( \small A_1 A_3\) подставим сумму \( \small A_1A_2+A_2A_3 \) из (1), которая больше, чем \( \small A_1 A_3\). Тогда получим:

Поседнее неравенство означает, что длина невырожденной ломаной больше расстояния между первым и последним точками.

Аналогично доказывается теорема для ломанной с любым количеством звеньев.

Источник

Смежность, инцидентность, степени вершин

Если х = – ребро графа, то v, w называются концами ребра х, в этом случае говорят, что ребро х соединяет вершины v и w.

Вершины v, w графа G(V,X) называются смежными, если ÎХ.

Два ребра называются смежными, если они имеют общую вершину.

Рассмотрим граф на рисунке 13.1.

Вершины v₅, v₆ – смежные, т.к. 5, v₆>- ребро. Вершины v₅, v₃ – не смежные, т.к. нет ребра их соединяющего.

Степень вершины v – это количество ребер графа, инцидентных этой вершине. Обозначение d (v).

Заметим, что вклад каждой петли равен двум.

Если степень вершины равна единице, то такая вершина называется висячей.

Если степень вершины равна нулю, то такая вершина называется изолированной.

Значит, вершины v₁ и v₄ – висячие, а вершина v₇ – изолированная.

Теорема о сумме степеней вершин графа: Для любого псевдографа G(V, X) выполняется равенство:

m – количество ребер графа. Действительно, каждое ребро графа инцидентно двум вершинам.

Проверим справедливость теоремы для графа 13.1:

m =7, 7× 2 =14 и 1+2+5+1+2+3+0 =14.

3. Способы задания графов

Один из способов задания графа уже рассмотрен – это геометрическое изображение, т.е. диаграмма.

Но при решении задач теории графов, осуществляемых на вычислительных машинах, такое задание не удобно. Граф должен быть представлен дискретным способом. Одно из направлений теории графов связано с их матричным представлением. Существуют различные виды матриц. Рассмотрим такие матричные формы, которые наиболее широко используются в алгоритмах на графах.

Матрица инцидентности графа.

Матрицей инцидентности графа G(V, X) называется матрица размера m´ n, элементы которой определяются следующим образом:

В любой строке матрицы инцидентности два или один элемент не равны нулю, т.к. каждое ребро соединяет две вершины, а если ребро – петля, то вершину саму с собой.

Матрица инцидентности однозначно определяет структуру графа, что позволяет читать всю необходимую информацию о графе. Например, выявлять изолированные и висячие вершины, петли; определять степени вершин. Информация о ребрах считывается по строкам, о вершинах – по столбцам.

Составим матрицу инцидентности для графа 13.1. Это матрица размера 7´ 7:

В первом и четвертом столбцах по одной единице, следовательно первая и четвертая вершины – висячие; в седьмом столбце все элементы равны нулю, значит седьмая вершина изолированная.

В третьей строке только один элемент не равен нулю, следовательно третье ребро- петля.

Суммируя элементы по столбцам с учетом того, что вклад петли равен двум, можно определить степень каждой вершины.

Матрицей смежности графа G(V, X) называется квадратная матрица n´ n, элементы которой определяются следующим образом:

Составим матрицу смежности для графа 13.1. Это квадратная матрица размера 7´ 7:

Матрица смежности неориентированного графа симметрична относительно главной диагонали.

Если есть не равные нулю элементы главной диагонали, то это означает наличие петель в графе. Читать информацию о графе можно и по столбцам и по строкам.

Сумма элементов верхнего или нижнего треугольника вместе с главной диагональю равна количеству ребер в графе. Для нашего графа сумма равна (учитывая только элементы не равные нулю): 1+1+1+2+1+1=7.

Далее рассматривая некоторые задачи теории графов будем использовать именно такой способ задания графа.

4. Маршруты в неориентированном графе

Для графа 13.1 построим маршрут, соединяющий вершину v₁ с вершиной v₅ :

Допускается краткая запись маршрута. В том случае, если в маршруте нет кратных ребер, то составляют последовательность только из вершин.

Если в маршруте есть кратные ребра, то в последовательность включают начальную вершину, ребра и конечную вершину. Или пользуются комбинированной записью: в последовательность включают все вершины и только кратные ребра.

Длиной маршрута l называется количество ребер в нем.

В нашем маршруте 5 ребер, значит его длина l =5.

Познакомимся с видами маршрутов.

Виды незамкнутых маршрутов:

Незамкнутый маршрут, в котором все ребра попарно различны называется цепью.

Цепь, в которой все вершины попарно различны называется простой цепью.

Виды замкнутых маршрутов:

Замкнутый маршрут, в котором все ребра попарно различны называется циклом.

Цикл, в котором все вершины попарно различны называется простым циклом.

Заметим, что петля или кратное ребро являются простыми циклами.

Составим различные маршруты для приведенного ниже графа на рисунке 13.5.

5. Операции над графами.

Кроме этих операций познакомимся с понятиями : подграф и сурграф.

Сурграфом графа G(V, X) называется граф G”(V, X”), где V=V, X” Ì X.

На рисунке 13.6 представлен собственный подграф графа 13.5.

На рисунке 13.7 – подграф графа 13.5, порожденный множеством V₁ =1, v₂, v₄, v₆>.

На рисунке 13.8 – сурграф графа 13.5.

6. Связность. Компоненты связности

Пусть дан псевдограф G(V,X).

Две вершины v и w называются связанными (или вершина v достижима из w), если :

б) существует маршрут, связывающий вершины v и w.

Определенное на множестве V отношение достижимости или связности является бинарным эквивалентным отношением (проверьте самостоятельно). А значит, множество V можно разбить на классы эквивалентности V₁ V₂ …V_k, где V₁ ÈV₂È …ÈV_k=V и V₁ ÇV₂ Ç…ÇV_k = Æ.

Все вершины, принадлежащие одному подмножеству Vi связанные, а вершины, принадлежащие разным подмножествам – несвязанные.

Каждое подмножество Vi называется компонентой связности графа G(V,X).

Согласно выше сказанному можно сформулировать определение компоненты связности следующим образом:

Компонента связности графа G(V,X) – это связный подграф, не являющийся собственным подграфом никакого другого связного подграфа графа G(V,X).

Количество компонент связности графа G(V,X) обозначается P(G).

На рисунке 13.9 представлен граф, у которого три компоненты связности, т.е. P(G) =3: G₁, G₂, G₃

Введем понятие связного графа.

Граф G(V,X) называется связным, если любые две его вершины достижимы (связанные).

Или: граф G(V,X) называется связным, если P(G) = 1.

Тогда, несвязный граф имеет P(G) >1.

С понятием компонента связности связаны понятия: разделительная вершина (точка сочленения) и мост.

Введем еще одну операцию над графом – удаление вершины.

Операцией удаления вершины называется удаление некоторой вершины вместе с инцидентными ей ребрами.

Если удаление вершины увеличивает количество компонент связности графа, то такая вершина называется точкой сочленения или разделительной вершиной.

Ребро, при удалении которого увеличивается количество компонент связности графа, называется мостом.

Для графа 13.5 найдем все разделительные вершины и мосты:

Источник