Что значит пятая часть отрезка

Длина отрезка

Для того, чтобы найти длину отрезка, его сравнивают с отрезком принятым за единицу измерения, который носит название единичный отрезок.

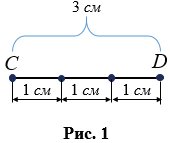
Если за единицу измерения принять сантиметр, то, чтобы определить длину отрезка, нужно узнать сколько раз в этом отрезке укладывается сантиметр. На рис.1 в отрезке СD сантиметр укладывается ровно три раза, значит, длина отрезка СD равна 3 см, можно записать СD = 3 см. В данном случае, для измерения удобно использовать сантиметровую линейку.

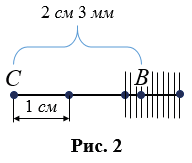
Бывает, что единичный отрезок не укладывается целое число раз в измеряемый отрезок, тогда единичный отрезок делят на 10 равных частей и определяют сколько раз одна десятая часть укладывается в остатке измеряемого отрезка. На рис.2 в отрезке СВ сантиметр укладывается 2 раза и в остатке 3 раза укладывается одна десятая часть сантиметра, значит, длина отрезка СВ равна 3,3 см или, учитывая что для сантиметра десятая часть равна миллиметру, 3 см 3 мм, т.е. можно записать СВ = 3,3 см (СВ = 3 см 3 мм).

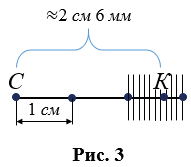
Может получится так, что и в миллиметрах остаток не укладывается целое число раз, тогда:

За единицу измерения можно принимать не только сантиметр, но и другие отрезки, например, дециметр, метр и т.д.

Свойства длин отрезков:

Поделись с друзьями в социальных сетях:

Источник

Урок 3 Бесплатно Отрезок. Длина отрезка

Начнем знакомство с одним из разделов математики, который называется геометрия.

Становление данной науки происходило тысячелетиями.

Сегодня обратим внимание на основные, базовые геометрические фигуры, такие как точка и отрезок.

Узнаем, что называют ломаной линией, какие геометрические фигуры называют многоугольниками, рассмотрим их основные элементы и характеристики.

Научимся сравнивать, находить длины отрезков.

Познакомимся с различными единицами измерения отрезков.

Рассмотрим свойства измерения длин отрезков.

Отрезок

Геометрическая фигура- это математическая модель, в которой рассматривается только форма и размер, не обращая внимания на иные свойства и состояния (цвет, из какого материала изготовлены, в каком состоянии находятся).

Как здания складываются из кирпичиков, так и сложные геометрические фигуры состоят из базовых фигур.

Одной такой элементарной фигурой является точка.

В реальности моделью, которая дает представление о точке может стать, например, след, оставленный острием карандаша, или отверстие на бумаге от швейной иглы.

Слово «точка» с латинского языка означает мгновенное касание, укол.

Точку принято рассматривать как некоторое место в пространстве или на плоскости.

Принято обозначать точки заглавными латинскими буквами (А, В, С и т.д.).

Две точки на плоскости можно соединить бесконечным множеством линий.

Самой короткой линией, соединяющей две точки на плоскости, будет прямая, проведенная по линейке через эти две точки.

Кратчайшая линия между двумя точками называется отрезком.

Любые две точки можно соединить только одним отрезком.

Точки, ограничивающие отрезок, называются концами отрезка.

Отрезок обозначают указанием имен его концов.

Через точки А и В с помощью линейки провели прямую.

Так как отрезок обозначают именами точек, получим отрезок АВ или ВА.

Пишут и говорят так: «Отрезок АВ» или «Отрезок ВА».

В названии отрезка не важно в каком порядке указываются его концы.

Отрезок можно построить с помощью линейки.

Для этого необходимо к отмеченным на плоскости точкам приложить линейку и провести прямую от одного конца отрезка до другого.

Чтобы с помощью линейки начертить отрезок, который длиннее чем сама линейка, нужно поступить следующим образом:

Между точками А и В отметить точку С.

Затем передвинем линейку так, чтобы левый конец линейки оказался около точки С, по правому концу линейки отложим точку D.

Последовательно соединив концы отрезков, получится отрезок AD, который длиннее, чем линейка.

У меня есть дополнительная информация к этой части урока!

Давайте разберемся, как могут располагаться точки по отношению к отрезку:

1. Точка лежит на отрезке.

Говорят: «Точка G принадлежит отрезку ».

Записывают это так: G ∈ AB

2. Точка не лежит на отрезке.

Говорят: «Точка не принадлежит отрезку ».

Записывают это так: R ∉ AB

Пройти тест и получить оценку можно после входа или регистрации

Длина отрезка

Каждый отрезок имеет определенную длину, значение которой является числом.

Так как каждый отрезок имеет длину, отрезки можно измерять и сравнивать.

Существует несколько способов сравнения отрезков.

1. Приблизительный способ сравнения.

Данный способ сравнения применяют только в том случае, когда длины отрезков явно отличаются.

Пример: Даны два отрезка АВ и ЕР

Очевидно, что отрезок АВ длиннее отрезка ЕР, значит, АВ > ЕР

Метод заключается в следующем: совмещаются два отрезка друг с другом так, чтобы совпали их концы с одной стороны.

По расположению других концов относительно друг друга можно оценить какой из отрезков длиннее, а какой короче.

Если при наложении отрезков друг на друга длины отрезков совпадут, то отрезки равны (отрезки в этом случае будут равными фигурами).

Если при наложении отрезков друг на друга один из отрезков будет составлять часть второго, то первый отрезок является короче второго (т.е. длина первого меньше длины второго).

Пример: Даны два отрезка АВ и ОЕ

Сравним данные отрезки методом совмещения отрезков.

Совместим левый конец А отрезка АВ и левый конец О отрезка ОЕ.

Можно заметить, что отрезок ОЕ составляет часть отрезка АВ.

Значит, отрезок ОЕ короче отрезка АВ.

Данный метод удобен, если есть возможность перемещать отрезки, совмещать один с другим.

3. Сравнение отрезков с помощью измерителя.

Если нет возможности перемещать сравниваемые отрезки, то можно использовать промежуточный измеритель.

В математике для этих целей используют специальный чертежный инструмент, который называется циркулем.

Чтобы сравнить отрезки с помощью циркуля, необходимо совместить концы отрезка с ножками циркуля.

Не меняя раствор циркуля, приложить его ко второму отрезку и сравнить.

Если нет возможности сравнить отрезки наложением и нет циркуля под рукой, то в качестве измерителя можно использовать нитку.

В таком случае нужно нитку приложить к исходному отрезку, на нитке по отрезку сделать замер, затем нитку приложить ко второму отрезку, оценить расположение замера на нитке по отношению к исследуемому отрезку, сделать вывод.

Пусть даны три отрезка СD, АЕ, BG

Сравним эти отрезки с помощью циркуля.

Соединим ножки циркуля с концами С и D отрезка СD.

Приложим циркуль с заданным раствором к отрезку АЕ.

Концы измерителя совпали с точками отрезка АЕ, значит, отрезки CD и AE равны: (CD = AE).

Приложим циркуль с заданным раствором к отрезку BG.

Отрезок выходит за концы измерителя, т.е. является частью отрезка BG, следовательно, отрезок BG длиннее отрезка СD: (BG > СD).

Все рассмотренные способы сравнения длины отрезков проводят без определения значения длины сравниваемых отрезков.

4. Существует еще один способ сравнения длины отрезков путем измерения их длинны.

Для этого необходимо сначала измерить длину каждого отрезка, далее сравнить полученные значения их длины и сделать вывод.

Большим будет являться тот отрезок, длина которого больше.

Соответственно, если длины измеряемых отрезков равны, то и отрезки равны.

У меня есть дополнительная информация к этой части урока!

Ломаная линия

Если последовательно соединить отрезки так, чтобы конец одного отрезка являлся началом следующего (при этом соседние отрезки не лежат на одной прямой), то образуется геометрическая фигура, которая называется ломаной линией.

Отрезки, из которых состоит ломаная линия, называют звеньями.

Концы отрезков называют вершинами ломаной.

Самые крайние вершины ломаной называют концами ломаной

Обозначение ломаной линии составляют из названий вершин этой ломаной, называя их по порядку.

Длиной ломаной называется сумма длин всех ее звеньев.

На рисунке изображена ломаная линия АBCDE.

Вершины ломаной АBCDE: А, B, C, D, Е.

Звенья ломаной АBCDE: AB, BC, CD, DE.

Найдем длину ломаной АВСDE:

АВСDE = AB+ BC+ CD+ DE = 2 см + 3 см + 4 см + 5 см = 14 см

Ломаная, концы которой совмещаются, называется замкнутой.

Многоугольником называется фигура, ограниченная замкнутой ломаной линией, звенья которой не пересекаются.

Отрезки (звенья) ломаной линии называют сторонами многоугольника.

Общие точки двух отрезков (сторон) многоугольника называют его вершинами.

Каждая пара сторон многоугольника, сходящиеся в одной точке, образуют углы многоугольника.

Количество сторон и количество углов в многоугольнике совпадают.

Вершины, стороны и углы многоугольника обозначаются аналогично ломаной линии.

Многоугольник принято обозначать и называть по его вершинам, начиная с любой вершины и называя их последовательно, в любом порядке.

На рисунке изображен многоугольник АBCDEF.

Вершины многоугольника АBCDEF: А, B, C, D, Е, F.

Стороны многоугольника АBCDEF: AB, BC, CD, DE, EF, FA.

Любые многоугольники можно сравнить: два многоугольника называются равными, если они совпадают при наложении.

Зная длину каждой стороны многоугольника, можно найти периметр этого многоугольника.

Периметр многоугольника принято обозначать заглавной латинской буквой Р

Найдем периметр многоугольника АBCDEF (изображенного на рисунке):

Р_АВСDEF = AB+ BC+ CD+ DE+ EF+ FA = 2 см + 3 см + 2 см + 2 см + 3 см + 2 см = 14 см.

Существует огромное множество различных видов многоугольников.

Обычно многоугольники различают по числу сторон и углов.

Многоугольник с наименьшим числом вершин, сторон и углов называют треугольником.

Треугольник часто обозначают символом «Δ» и тремя заглавными латинскими буквами, которые обозначают его вершины.

На рисунке изображен треугольник АBC (Δ АBC).

Отрезки AB, BC, АC— стороны треугольника АBC.

Периметр треугольника- это сумма длин трех его сторон.

Найдем периметр треугольника АBC (изображенного на рисунке):

Р_АВС = AB+ BC+ АС = 4 см + 6 см + 3 см = 13 см.

Пройти тест и получить оценку можно после входа или регистрации

Источник

Отрезок. Ломаная линия

Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.

Рис. 1 Отрезок на прямой

Рис. 2 Несколько отрезков на прямой

Отрезок делит прямую линию на три объекта (смотри рисунок 3):

То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.

Рис. 3 Отрезок и лучи прямой

Рис. 4 Отрезок без прямой

Рис. 5 Отрезок и принадлежащие ему точки

Так, на рисунке 5 видно, что:

В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.

Рис. 6 Отрезок и части отрезка

Построение и измерение отрезка

Произвольный отрезок можно построить двумя способами:

Рис. 7 Построение произвольного отрезка

Измерить отрезок можно:

Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).

Рис. 8 Сравнение отрезков

На рисунке 8 видно, что:

Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.

Длина отрезка – это расстояние между концами этого отрезка.

Равные отрезки — это такие отрезки, которые имеют одинаковую длину.

На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?

Рис. 9 Измерение длины отрезка

Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.

Рис. 10 Построение отрезка заданной длины

Отрезок — это самое короткое расстояние между двумя точками.

В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.

Рис. 11 Кривая, ломаная, отрезок

Ломаная линия

Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.

Рис. 12 Ломаная линия

На рисунке 12 видно, что:

Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.

Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.

Рис. 12. Замкнутая и разомкнутая ломаные линии

Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.

Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.

Рис. 13. Самопересекающиеся ломаные линии

Источник

ВОПРОСЫ

1. Сколько существует отрезков, концами которых являются две дан­ные точки?

2. Как обозначают отрезок?

3. Какие вы знаете единицы длины?

Нам известны такие единицы длины: миллиметр, сантиметр, дециметр, метр, километр.

4. Объясните, что означает измерить длину отрезка.

5. Каким свойством обладает длина отрезка?

6. Какие отрезки называют равными?

7. Какие длины имеют равные отрезки?

8. Какой из двух неравных отрезков считают большим?

9. Что называют расстоянием между точками А и В?

10. Объясните, какую геометрическую фигуру называют ломаной.

11. Что называют длиной ломаной?

12. Какую ломаную называют замкнутой?

РЕШАЕМ УСТНО

1. Какое число больше числа 46 на 9? Какое число меньше числа 72 на 15? Какое число больше числа 21 в 7 раз? Какое число меньше числа 65 в 13 раз?

2. Назовите все двузначные числа, сумма цифр которых равна 6.

3. Назовите все двузначные числа, разность цифр которых равна 7.

4. Назовите три последовательных натуральных числа, наименьшим из которых является наибольшее четырехзначное число.

5. Назовите три последовательных натуральных числа, наибольшим из которых является наименьшее четырехзначное число.

6. Выразите в сантиметрах:

1) 7 дм 4 см = 74 см
2) 4 м 1 см = 401 см
3) 2 м 6 дм = 260 см
4) 1 м 2 дм 5 см = 125 см

7. Выразите в дециметрах и сантиметрах:

1) 72 см = 7 дм 2 см
2) 146 см = 14 дм 6 см
3) 450 мм = 4 дм 5 см
4) 8 м 40 мм = 80 дм 4 см

УПРАЖНЕНИЯ

44. Запишите все отрезки, изображенные на рисунке 15.

a) AB, BC, AC, BK
б) OP, OR, OT, PR, PT, RT
в) AE, EC, CD, AC, ED, AD
г) MN, NE, ME, EP, PQ, EQ, MQ, NP

45. Запишите все отрезки, изображенные на рисунке 16.

а) AO, OC, AC, BO, OD, BD, AD
б) MK, KN, NP, MN, KP, MP, FK, KE, FE, EN, NS, ES

46. Отметьте в тетради точки A, B, C, D и соедините их попарно отрезками. Сколько отрезков образовлось? Сколько образовалось отрезков с концом в точке А?

47. Начертите отрезки MN и AC так, чтобы MN=6 см 3 мм, AC = 5 см 3 мм.

48. Начертите отрезки EF и BK так, что EF = 9 см 2 мм, BK = 7 см 6 мм.

49. Начертите отрезок АВ, длина которого равна 8 см 9 мм. Отметьте на нём точку С так, чтобы СВ = 3 см 4 мм. Какова длина отрез­ка АС?

50. Начертите отрезок TP, длина которого равна 7 см 8 мм. Отметьте на нём точку Е так, чтобы ТЕ = 2 см 6 мм. Какова длина отрезка ЕР?

51. Сравните на глаз отрезки АВ и CD (рис. 17). Проверьте свой вывод измерением.

52. Назовите все ломаные, изобра­жённые на рисунке 11. Какая из них имеет наибольшее коли­чество звеньев?

53. Назовите звенья ломаной, изображённой на рисунке 18, и измерьте их длины (в миллиметрах). Вычислите длину ломаной.

54. Запишите звенья ломаной, изображённой на рисунке 19, и измерь­те их длины (в миллиметрах). Вычислите длину ломаной.

55. Отметьте в узле клеток тетради точку А; точку В разместите на 4 клетки левее и на 5 клеток выше точки А; точку С — на 3 клет­ки правее и на 1 клетку выше точки В; точку D — на 3 клетки пра­вее и на 3 клетки ниже точки С; точку Е — на 1 клетку правее и на 2 клетки ниже точки D. Соедините последовательно отрезками точ­ки А, В, С, D и Е. Какая фигура образовалась? Запишите её назва­ние и укажите количество звеньев.

56. Вычислите длину ломаной ABCDE, если АВ = 8 см, ВС = 14 см, CD = 23 см, DE = 10 см.

57. Вычислите длину ломаной MNKPEE, если MN = 42 мм, NK = 38 мм, КР = 19 мм, РЕ = 12 мм, ЕF = 29 мм.

58. Начертите в тетради ломаную, изображённую на рисунке 20. Измерьте длины звеньев (в мил­лиметрах) и найдите длину ло­маной.

59. Известно, что отрезок SK в 3 ра­за больше отрезка RS (рис. 21). Найдите длину отрезка RK, ес­ли RS = 34 см.

60. Известно, что отрезок DВ в 5 раз меньше отрезка AD (рис. 22). Найдите длину отрезка АВ, ес­ли АD = 135 см.

61. Известно, что AC = 32 см, ВС = 9 см, CD = 12 см (рис. 23). Найдите длины отрезков АВ и BD.

62. Известно, что MF= 43 см, МЕ = 26 см, КЕ = 18 см (рис. 24). Найди­те длины отрезков МК и EF.

63. Даны две точки А и В. Сколько можно провести отрезков, соеди­няющих эти точки? Сколько можно провести ломаных, соединяю­щих эти точки?

64. Начертите отрезок МК и отметьте на нём точки А и С. Запишите все образовавшиеся отрезки.

65. Длина отрезка АВ равна 28 см. Точки М и К принадлежат этому от­резку, причём точка К лежит между точками М и В, AM =12 см, ВК = 9 см. Найдите длину отрезка МК.

66. Точка С принадлежит отрезку АВ, длина отрезка АС равна 15 см, а отрезок АВ на 5 см больше отрезка АС. Чему равна длина отрез­ка ВС? Есть ли в условии задачи лишние данные?

67. Отрезки МТ и FK равны (рис. 25). Сравните отрезки MF и ТК.

68. Постройте ломаную ACDM так, чтобы АС = 15 мм, CD = 24 мм, DM = 32 мм. Вычислите длину ло­маной.

69. Постройте ломаную CEFK так, чтобы звено СЕ было равно 8 мм, звено EF было на 14 мм больше звена СЕ, а звено FK — на 7 мм меньше звена EF. Вычислите длину ломаной.

70. Вычислите длину ломаной, изображённой на рисунке 26.

71. Известно, что АС = 8 см, BD = 6 см, ВС = 2 см (рис. 27). Найдите длину отрезка AD.

72. Известно, что MF = 30 см, ME = 18 см, KF = 22 см (рис. 28). Найди­те длину отрезка КЕ.

73. Известно, что КР = РЕ = EF = FT = 2 см (рис. 29). Какие ещё равные отрезки есть на этом рисунке? Найдите их длины.

74. На первом отрезке отметили семь точек так, что расстояние между любыми соседними точками равно 3 см, а на втором — десять точек так, что расстояние между любыми соседними точками равно 2 см. Расстояние между какими крайними точками больше: лежащими на первом отрезке или лежащими на втором отрезке?

75. Известно, что АЕ = 12 см, AQ = QB, ВМ = МС, СК = KD, DR = RE, МК = 4 см (рис. 30). Найдите длину отрезка QR.

76. Какое наименьшее количество точек надо отметить на отрезках, изображённых на рисунке 31, чтобы на каждом из них было две от­меченные точки, не считая концов отрезков?

77. У Миши есть линейка, на которой отмечены только 0 см, 5 см и 13 см (рис. 32). Как, пользуясь этой линейкой, он может постро­ить отрезок длиной: 1) 3 см; 2) 2 см; 3) 1 см?

УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ

78. Вычислите:

79. Выполните действия:

80. Детскому саду подарили четыре ящика конфет по 5 кг в каждом и шесть ящиков печенья по 3 кг в каждом. На сколько килограм­мов больше подарили конфет, чем печенья?

81. Медведица Настасия Петровна заготовила на зиму семь бочонков мёда по 12 кг в каждом и 8 бочонков мёда по 10 кг в каждом. Сколько всего килограммов мёда заготовила Настасия Петровна?

82. В магазин привезли 240 кг бананов и 156 кг апельсинов. Треть при­везённых фруктов продали в первый день, а остальные — во второй день. Сколько килограммов фруктов продали во второй день?

83. Кот Матроскин вырастил в своём саду 246 кг яблок и 354 кг груш. Шестую часть всех фруктов он отдал своим друзьям из детского са­да, пятую часть всех фруктов — друзьям из школы, а остальное — в больницу. Сколько килограммов фруктов Матроскин отдал в больницу?

84. Укажите наименьшее натуральное число, сумма цифр которого равна 101.

Источник