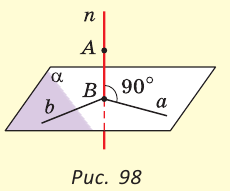
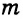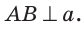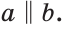Что значит перпендикулярные лучи

Что значит перпендикулярные лучи

Углы бывают острые, прямые и тупые.

Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.

Два угла с одной общей стороной называются смежными.

На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.

Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°

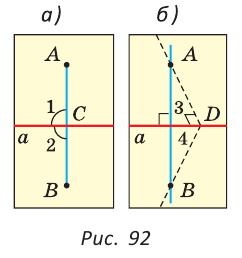
При пересечении двух прямых образуются четыре угла:

Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.

∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4

То же справедливо и для ∡1 и ∡3.

Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.

Перпендикулярность прямых принято обозначать так: a⟂b

Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!

Теорема о перпендикулярных прямых

Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.

Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.

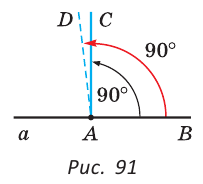
Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.

Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.

Свойство перпендикулярных прямых

Две прямые, перпендикулярные третьей, не пересекаются.

Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.

У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Попробовать бесплатно

Интересное по рубрике

Найдите необходимую статью по тегам

Подпишитесь на нашу рассылку

Мы в инстаграм

Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Посмотреть

Рекомендуем прочитать

Реальный опыт семейного обучения

Звонок по России бесплатный

Посмотреть на карте

Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.

Источник

Перпендикулярные прямые в геометрии с примерами

Определение: Две прямые называются перпендикулярными, если они пересекаются под прямым углом.

При пересечении двух перпендикулярных прямых образуются 4 прямых угла.

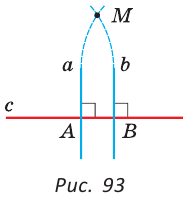
Отрезки и лучи называются перпендикулярными, если они лежат на перпендикулярных прямых. На рисунке 87 прямые

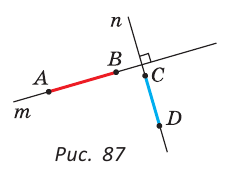
Определение. Перпендикуляром к данной прямой называется отрезок, который лежит на прямой, перпендикулярной данной, один из концов которого (основание перпендикуляра) является точкой пересечения этих прямых.

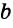
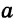
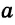
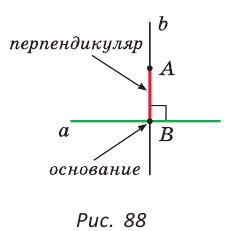
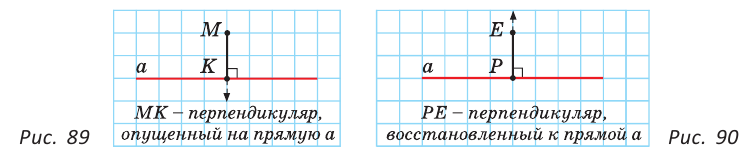
Прямая перпендикулярна прямой (рис. 88). Отрезок АВ — перпендикуляр к прямой , точка В — основание перпендикуляра. Точку В также называют проекцией точки А на прямую .

Если из точки М, которая не лежит на прямой , провести перпендикуляр МК к прямой (рис. 89), то получим перпендикуляр, опущенный из точки М на прямую . Если из точки Р, лежащей на прямой , провести перпендикуляр РЕ к прямой (рис. 90), то получим перпендикуляр, восстановленный (восставленный) к прямой .

Теорема. Через точку, лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой, и только одну.

Дано: прямая ; точка А; (рис. 91).

Доказать: через точку А можно провести прямую, перпендикулярную прямой , и только одну.

Доказательство:

По аксиоме откладывания углов от луча АВ в данную полуплоскость можно отложить угол CAB, равный 90°, и притом только один. Тогда прямая АС перпендикулярна прямой . Предположим, что существует другая прямая AD, проходящая через точку А и перпендикулярная прямой . Тогда и от луча АВ в данную полуплоскость будут отложены два угла, равные 90°: А это невозможно по аксиоме откладывания углов. Следовательно, не существует другой прямой, проходящей через точку А и перпендикулярной прямой .

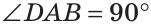
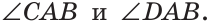
Теорема. Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой, и притом только одну.

Дано: прямая ; точка A, (рис. 92).

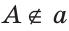
Доказать: через точку А можно провести прямую, перпендикулярную прямой , и притом только одну.

Доказательство:

1) В начале докажем, что через точку А можно провести прямую, перпендикулярную прямой . Мысленно перегнем лист с чертежом по прямой (совместим верхнюю полуплоскость с нижней, повернув ее вокруг прямой ) (рис. 92, а). Точка А займет некоторое положение, которое обозначим точкой В. Вернем полуплоскости в прежнее положение и проведем прямую АВ. Так как углы 1 и 2 совпадают при наложении полуплоскостей, то они равны. А поскольку эти углы смежные, то каждый из них равен 90° и

2) Теперь докажем, что АВ — единственная прямая, проходящая через точку А и перпендикулярная прямой . Пусть прямая AD также перпендикулярна прямой . Тогда (рис. 92,6). Совместим полуплоскости еще раз. Угол 3 совпадет с углом 4, значит Тогда — развернутый, и через точки А и В будут проходить две прямые: ранее проведенная прямая и прямая, проходящая через точки A, D и В. А это невозможно по аксиоме прямой. Следовательно, прямая AD не перпендикулярна прямой . Теорема доказана.

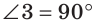
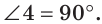
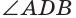
Из двух последних теорем следует, что на плоскости через любую точку можно провести прямую, перпендикулярную данной прямой, и притом только одну.

Теорема (о двух прямых, перпендикулярных третьей). На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Дано: 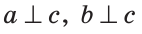(рис. 93).

Доказать:

Доказательство:

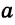
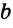
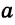
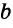
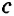
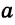
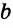
Если предположить, что прямые и пересекаются в некоторой точке М, то окажется, что через точку М проходят две прямые и , перпендикулярные третьей прямой , а это невозможно. Значит, прямые и лежат в одной плоскости и не пересекаются, то есть параллельны между собой. Теорема доказана.

Теорема, обратная данной

Если поменять условие и заключение теоремы местами, то получим утверждение, обратное данному. Для указанной выше теоремы получаем: «Если сумма двух углов равна 180°, то эти углы смежные». Но это утверждение неверно, поскольку можно привести пример двух углов, например, равных 60° и 120°, сумма которых 180°, но которые не являются смежными. Значит, приведенное утверждение не является теоремой.

Если же верно и обратное утверждение, то оно называется теоремой, обратной данной. Например, известна теорема: «Если сумма цифр числа делится на 3, то и число делится на 3» — и ей обратная: «Если число делится на 3, то и сумма цифр числа делится на 3».

Иногда прямую и обратную теоремы объединяют, употребляя при этом выражение «тогда и только тогда». Объединим вышеуказанные теоремы: «Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3».

Геометрия 3D

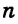
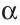
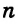
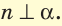
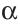
Пусть в пространстве прямая пересекает плоскость в точке В (рис. 98). Если прямая перпендикулярна любой прямой плоскости, проходящей через точку В, то она называется прямой, перпендикулярной плоскости. Пишут Отрезок АВ называется перпендикуляром к плоскости .

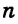
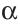
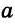
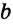
Чтобы прямая была перпендикулярна плоскости , достаточно, чтобы она была перпендикулярна каким-то двум прямым плоскости, проходящим через точку В. Например, прямым и .

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Урок 44 Бесплатно Перпендикулярные прямые

До этого на уроках математики мы работали с числами, буквами, выражениями.

Иногда не только писали, но и рисовали схемы, координатные прямые и рисунки, чтобы лучше разбираться в изучаемом вопросе.

Сегодня мы будем изучать геометрические понятия, а именно, что является прямой, а что нет, какие прямые называются перпендикулярными.

Также узнаем, как строить перпендикулярные прямые разными способами.

Основные определения

В геометрии есть два понятия, которые не имеют определения, их мы принимаем как аксиомы.

Это понятия точки и прямой.

Все остальные определения будут так или иначе выражаться через эти два понятия.

Заметим, что любая точка, лежащая на прямой, разделяет эту прямую на два луча.

Разделяющую точку также называют началом луча.

И еще немного формализма.

Эти лучи называют сторонами угла, а их общее начало вершиной угла.

Есть величины для измерения длины: метр, сантиметр, километр и прочие производные метра.

Для измерения угла используются другие величины: градусы, минуты, секунды, радианы.

Одним из наиболее простых приборов для измерения углов является транспортир. Достаточно приложить его прямую часть к одной стороне угла и посмотреть, какое деление совпадет со второй стороной угла.

Главное, быть внимательным и смотреть, с какой стороны находится внутренняя часть угла.

Допустим, имеется такая конфигурация:

Углы обычно обозначаются тремя буквами, где буква посередине обозначает вершину угла.

Величина угла AOB будет равняться 45-ти градусам, можно записать как \(\mathbf<45^\circ>\).

Если необходимо измерить угол BOC, то нужно из 180-ти градусов вычесть 45 градусов, так как метки на транспортире соответствуют величинам углов, если считать от нуля, а в данном случае луч ОС лежит на отметке 180.

Также часто перед буквенным обозначением угла ставят следующий знак: \(\mathbf<\angle>\), получаются такие записи: \(\mathbf<\angle AOB>\), \(\mathbf<\angle BOC>\).

Иногда, когда нет неоднозначности, угол могут обозначать и одной буквой, например \(\mathbf<\angle A>\)

На транспортире данная отметка находится посередине.

Если обычный угол часто обозначают маленькой дугой, то прямые углы принято обозначать таким квадратиком.

Прямой угол один из самых распространенных в мире: с большой вероятностью вы сейчас сидите в комнате с такиими углами, у вашего стола прямые углы, а также у окна и так далее.

Теперь мы подготовили все определения, чтобы определить термин из заголовка урока.

Определение: две прямые, образующие при пересечении прямые углы, называют перпендикулярными.

Прямые часто обозначают одной строчной латинской буквой. В данном случае прямые a и b перпендикулярные по определению, потому что образуют прямые углы.

Если бы они пересекались под другим углом или не пересекались бы, то они не были бы перпендикулярными. В данном случае прямые a и b не являются перпендикулярными.

Пройти тест и получить оценку можно после входа или регистрации

Построение прямого угла и перпендикулярных прямых

Перечислим основные способы в порядке возрастания сложности.

Самый простой способ взять предмет с прямым углом- чертежный треугольник, линейку, банковскую или проездную карту (придется только дорисовать скошенный угол от руки), и обвести его.

Правда, мы не можем гарантированно полагаться на перечисленные кроме треугольника предметы, так как они не предназначены для черчения, и угол может быть не совсем прямым.

Лучи, являющиеся сторонами угла, будут перпендикулярны, а значит, будут частями перпендикулярных прямых.

Также можно построить любой угол, в том числе прямой, с помощью транспортира.

1) Вершину угла мы ставим в центре прямой части транспортира.

2) Одни сторону проводим по прямой части транспортира в сторону нуля.

3) Ставим метку напротив риски с соответствующей величиной угла.

4) Соединяем вершину угла с меткой.

Аналогичным образом строится прямой угол.

В таком случае его стороны опять же будут перпендикулярными лучами, следовательно, частями перпендикулярных прямых.

Прежде чем перейти к более сложному и интересному способу, надо упомянуть, что клетки в тетради начерчены перпендикулярными прямыми, поэтому можно от руки обвести одну вертикальную линию и одну горизонтальную.

Скорее всего линии получатся не совсем прямыми, но если это нужно для какой-то схемы в черновике, то почему бы и нет.

Хотя конечно же во всех работах лучше использовать приборы и линейку чтобы рисунок был максимально красивым.

Интересно, что перпендикулярные прямые можно построить с помощью циркуля и линейки без разметки (ну и карандаша/ручки, конечно же).

Подробнее, почему алгоритм является корректным, вы узнаете в курсе геометрии за 7-й класс, но пока что посмотрим на сам алгоритм.

1) Чертим прямую и отмечаем на ней точку (назовем ее О).

2) Ставим в эту точку циркуль и с помощью него делаем две пометки, получаем две точки, равноудаленные от первой точки (назовем из А и В).

3) Проводим из каждой из точек А и В окружности одинакового радиуса, или лучше только нужные их части, так чтобы получить хотя бы одно пересечение (назовем его точной С).

4) Соединяем точку С с исходной точкой О, готово, мы получили перпендикулярную прямую, причем проходящую через точку, которую мы сами выбрали.

В этом алгоритме важна аккуратность: если точки А и В будут на разном расстоянии от центра или окружности из точек А и В будут разного радиуса, прямая может получится не перпендикулярной.

Пройти тест и получить оценку можно после входа или регистрации

Источник