Что означает слово алгебра для 7 класса

Алгебра

А́лгебра (от араб. الجبر ‎‎, «аль-джабр» — восполнение [1] ) — раздел математики, который можно грубо охарактеризовать как обобщение и расширение арифметики. Слово «алгебра» также употребляется в названиях различных алгебраических систем. В более широком смысле под алгеброй понимают раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающий обычные операции сложения и умножения чисел.

Алгебра — это наука, изучающая алгебраические системы с точностью до изоморфизма.

Алгебраическая система — упорядоченная пара множеств . Первое множество () — элементы какой либо природы (числа, понятия, буквы). Второе множество () — операции над первым множеством (сложение, умножение, возведение в степень). Примеры: группа, кольцо, поле.

Содержание

История

Истоки алгебры уходят к временам глубокой древности. Ещё 4000 лет назад вавилонские учёные могли решать квадратные уравнения. Тогда никаких обозначений не было, и уравнения записывались в словесной форме. Первые обозначения появились в Древней Греции благодаря учёному Диофанту. Неизвестное число он назвал «ἀριθμός», вторую степень неизвестного — «δύναμις», третью «κύβος», четвёртую — «дюнамодюнамис», пятую — «дюнамокюбос», шестую — «кюбоккюбос». Все эти величины он обозначал сокращениями (ар, дю, кю, ддю, дкю, ккю). Ни вавилоняне, ни греки не знали и не признавали отрицательные числа.

За 2000 лет до нашего времени китайские учёные решали уравнения первой степени и их системы, а также квадратные уравнения. Они уже знали отрицательные и иррациональные числа. Поскольку в китайском языке каждый символ обозначает понятие, то сокращений не было. В 13 веке китайцы открыли закон образования биномиальных коэффициентов, ныне известный как «треугольник Паскаля». В Европе он был открыт лишь 250 лет спустя. [2]

В 12 веке алгебра попала в Европу. С этого времени начинается её бурное развитие. Были открыты способы решения уравнений 3 и 4 степеней. Распространения получили отрицательные и комплексные числа. Было доказано, что любое уравнение выше 4 степени нельзя решить алгебраическим способом.

Вплоть до второй половины XX века практическое применение алгебры ограничивалось, в основном, решением алгебраических уравнений и систем уравнений с несколькими переменными. Во второй половине XX века началось бурное развитие ряда новых отраслей техники. Появились электронно-вычислительные машины, устройства для хранения, переработки и передачи информации, системы наблюдения типа радара. Проектирование новых видов техники и их использование немыслимо без применения современной алгебры. Так, электронно-вычислительные машины устроены по принципу конечных автоматов. Для проектирования электронно-вычислительных машин и электронных схем используются методы булевой алгебры. Современные языки программирования для ЭВМ основаны на принципах теории алгоритмов. Теория множеств используется в системах компьютерного поиска и хранения информации. Теория категорий используется в задачах распознавания образов, определении семантики языков программирования, и других практических задачах. Кодирование и декодирование информации производится методами теории групп. Теория рекуррентных последовательностей используется в работе радаров. Экономические расчеты невозможны без использования теории графов. Математическое моделирование широко использует все разделы алгебры.

Классификация

Алгебру можно грубо разделить на следующие категории:

В некоторых напралениях углублённого изучения, аксиоматические алгебраические системы, такие как группы, кольца, поля и алгебры над полем на присутствие геометрических структур (метрик и топологий), совместимых с алгебраическими структурами. Список некоторых разделов функционального анализа:

Элементарная алгебра

Элементарная алгебра — раздел алгебры, который изучает самые базовые понятия. Обычно изучается после изучения основных понятий арифметики. В арифметике изучаются числа и простейшие (+, −, ×, ÷) действия с ними. В алгебре числа заменяются на переменные (a,b,c,x,y и так далее). Такой подход полезен, потому что:

Источник

Что такое алгебра?

Знакомство с предметом «алгебра». История ее возникновения.

Просмотр содержимого документа
«Что такое алгебра?»

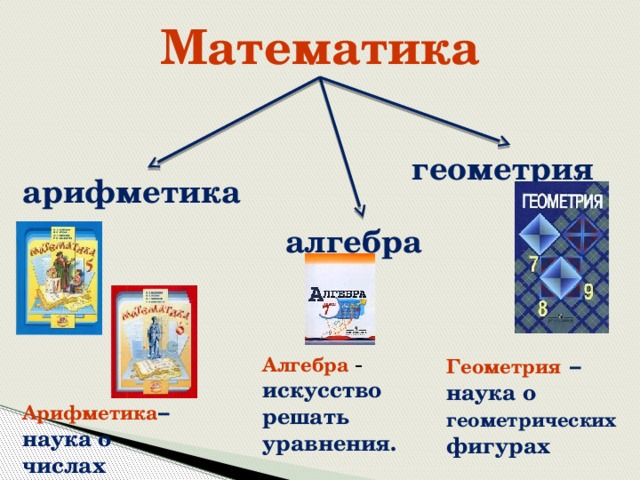
Геометрия – наука о геометрических фигурах

Алгебра – искусство решать уравнения.

Арифметика – наука о числах

А конкретнее, на страничку повторения всего того, что вы узнали в 5-6 классах.

Повторение проведем в форме игры.

Вы же любите играть?!

Сейчас вы получите листики, куда вы фломастером запишите:

Время выполнения или регламентирует учитель, или происходит ориентация на выполнения задания примерно одной пятой всех учащихся. В последнем случае ученики, выполнившие задание встают со своего места, что тоже является “подстегивающим” стимулом для остальных.

Проверку ответов можно провести несколькими способами:

1) листы сдаются на проверку учителю, при этом каждому выставляется оценочный балл в журнал;

2) учащиеся по просьбе учителя поднимают листы вверх, учителю сразу видно как каждый справился с заданием;

3) учащиеся самостоятельно сравнивают свои ответы с образцом верных ответов (на доске, на листе учителя и т.д.), при этом возможна взаимопроверка в парах.

устно решите примеры, ответы впишите на листы:

“ Поломка” – задание: среди решенных примеров, найдите те, которые содержат ошибки-“поломки”. Ответ запишите в виде числа, цифры в котором соответствуют номерам “поломок”:

чтобы пересечь финишную прямую необходимо быстро решить пример и ответ записать на листик:

Сдаем работы учителю.

Итак, каков ответ этого примера? 5! Отлично . Я вам желаю, что бы ваши знания всегда оценивались таким баллом!

А далее мы будем работать

Приложение 1 (задания для групп)

Приложение 2 ( задания для каждого учащегося)

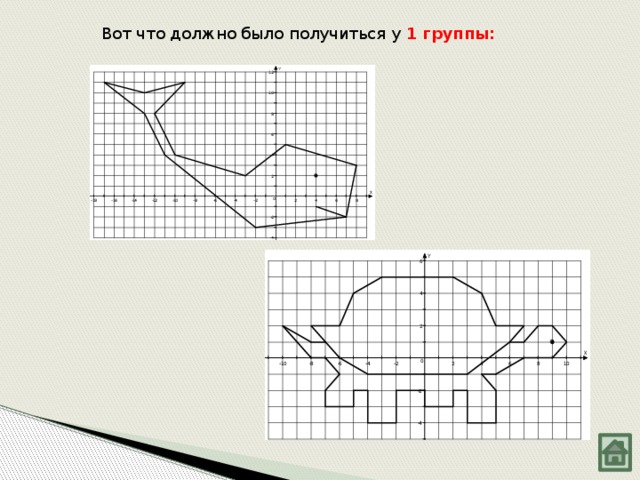
Вот что должно было получиться у 1 группы:

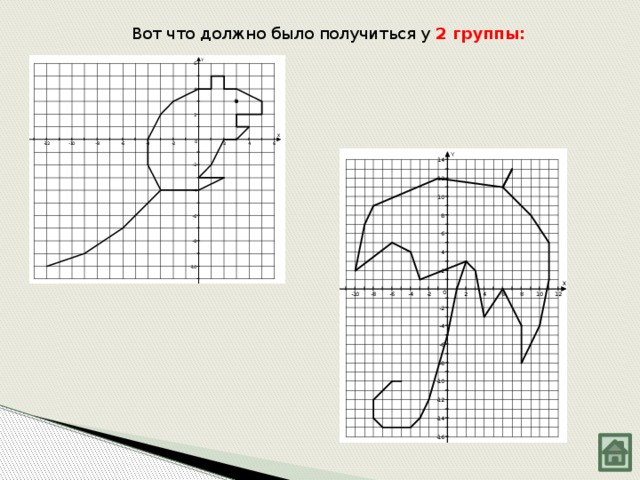
Вот что должно было получиться у 2 группы:

Вот что должно было получиться у 3 группы:

Вот что должно было получиться у 4 группы:

Вот что должно было получиться у 4 группы:

А теперь окунемся в историю.

Другой раздел математики посвящен различным фигурам и их свойствам, называется он ГЕОМЕТРИЕЙ

Почти все науки зародились в Греции, один из разделов математики получил греческое название « АРИФМЕТИКА »

А вот слово « АЛГЕБРА » не греческое

Абу Абдалах Мухаммед ибн Муса ал-Хорезми – выдающийся средневековый ученый, внесший большой вклад в развитие математики, астрономии, математической географии.

Предполагают, что он родился в городе Хиве, о его жизни почти ничего не известно. Научной работой аль-Хорезми в основном занимался в Багдаде. Его труды в течение нескольких веков оказывал сильное влияние на ученых Востока и Запада.

Аль-Хорезми первым написал книгу на арабском языке о решении уравнений

«Китаб мухтасар аль джебр ва-л-мукабала»

При решении уравнения

Если в части одной,

Встретится член отрицательный,

С этим членом сличив,

Равный член придадим,

И найдем результат нам желательный

Дальше смотрим в уравнение,

Можно ль сделать приведенье,

Если члены в нем подобны,

Сопоставить их удобно,

Вычтя равный член из них,

К одному приводим их.

Сам он слово «алгебра»

не применял. И называл

Что же изучает алгебра?

«Алгебра есть не что иное, как математический язык, приспособленный для обозначения отношений между количествами». И. Ньютон

Обозначив искомое число лет через х, составим уравнение:

В сохранившихся до наших дней математических папирусах имеются не только задачи, которые приводят к уравнениям первой степени с одним неизвестным, как в задаче о возрасте братьев, но и задачи, приводящие к уравнениям вида ax 2 =b.

Более подробно с историей математики вы сможете ознакомиться

на сайте Википедии

в разделе История математики

Стр. 226-230 учебник – справочные материалы по 5-6 классам.

Источник

Значение слова «алгебра»

[Лат. algebra из араб.]

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

А’ЛГЕБРА, ы, мн. нет, ж. [от араб.]. Отдел математики, часть математического анализа (см. анализ).

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

а́лгебра

1. раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающих обычные операции сложения и умножения чисел

2. то же, что элементарная алгебра, раздел алгебры [1], охватывающий свойства операций с вещественными и комплексными числами, а также правила тождественных преобразований математических выражений и уравнений с использованием символов, обозначающих такие числа, и элементарных функций

3. тип алгебраических структур; множество из каких-либо объектов, над элементами которого определены некоторые операции, являющиеся, как правило, обобщением сложения и умножения

4. книжн. сложная система навыков, знаний, методов в какой-либо области ◆ Нужны объективные методы оценки эффективности производств, включающие в себя не только арифметику, но и социальную алгебру нашей действительности. Марина Наумова, «Рыба ищет где глубже», 2001 г. ◆ Очень грубый подсчёт показывает абсолютное преобладание тех, кто может выиграть от дерегулирования занятости. Почему тогда реформы в этой сфере остаются столь сложными с политической точки зрения? Почему аргумент от простой арифметики в их поддержку недостаточен, а необходима хитроумная алгебра политических комбинаций? Владимир Гимпельсон, «Пора дерегулировать?», 2003 г.

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова накусывать (глагол), накусывали:

Источник