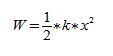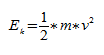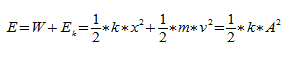Что называют периодом колебаний маятника в физике

Амплитуда, период, частота колебаний.

Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.

Для маятника это максимальное расстояние, на которое удаляется ша­рик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.

Амплитуда колебаний измеряется в единицах длины — метрах, санти­метрах и т. д. На графике колебаний амплитуда определяется как макси­мальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).

Период колебаний.

Период колебаний — это наименьший промежуток времени, через который система, соверша­ющая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.

Другими словами, период колебаний (Т) — это время, за которое совершается одно полное ко­лебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.

За полный период колебаний, таким образом, тело проходит путь, равный четы­рем амплитудам. Период колебаний измеряется в единицах времени — секундах, минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).

Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющей­ся величины точно повторяются через определенный промежуток времени, т. е. для гармоничес­ких колебаний. Однако это понятие применяется также и для случаев приблизительно повторяю­щихся величин, например, для затухающих колебаний.

Частота колебаний.

Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.

Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:

.

В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:

.

Циклическая частота — это число колебаний, совершаемых за 2π секунд.

Источник

Период колебаний

Из Википедии — свободной энциклопедии

В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени.

Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическим колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).

В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.

Единицы измерения: секунда и, в принципе, вообще единицы измерения времени.

Период колебаний связан соотношением взаимной обратности с частотой:

В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта — например, частицы — есть частота [3] колебаний его волновой функции).

Теоретическое вычисление периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно — и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).

Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно — через длину волны, для чего применяются интерферометры, дифракционные решётки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).

Источник

Период колебаний

Что такое колебательный процесс

Колебания — это движения или процессы, которые повторяются с определенным интервалом времени.

Систему, совершающую колебания, называют колебательной системой или осциллятором.

Исходя из физической природы, колебательные процессы бывают механического, электромагнитного и других видов.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Свободные или собственные колебания — колебания, которые наблюдают в системе, предоставленной себе после выведения из равновесного состояния.

Вынужденными колебаниями называют колебания, происходящие под действием внешней силы, изменяющейся периодически.

При механических колебаниях, которые относят к категории вынужденных:

Гармоническими колебаниями называют колебания, определяемые физической величиной, которая изменяется, согласно закону синуса или косинуса.

Разные периодические процессы, повторяющиеся в течение равных временных интервалов, могут быть записаны в виде суммы или суперпозиции гармонических колебаний.

Определение периода колебаний, формула

Колебательный процесс можно представить в виде уравнения. Тогда гармоническое колебание значения х будет представлено следующей формулой:

\(x(t)=A\times \cos \left(\omega _<0>t+\phi _ <0>\right)\)

Где \(x(t)\) является отклонением колеблющейся физической величины от равновесного значения;

А представляет собой амплитуду гармонических колебаний;

\(\omega _<0>\) равно циклической или круговой частоте колебаний;

\(\phi _<0>\) является начальной фазой колебаний, характерной для момента времени t=0, что можно определить с помощью выбора начала отсчета времени;

\(cp(t)=(co_<0>t+cp_<0>)\) описывает фазу колебаний в момент времени t, определяется в радианах, соответствует значению колеблющейся величины в данное время.

\(\cos \left(\alpha +2\pi \right)=\cos \alpha,\)

Период колебаний Т представляет собой минимальный временной интервал, в течение которого колебательная система возвращается в то состояние, в котором она находилась в начальный момент времени, определенный произвольно.

В этом случае фаза будет увеличена на \(2\pi:\)

\(\omega _<0>(t+T)+\phi _<0>=\left(\omega _<0>t+\phi _ <0>\right)+2\pi\)

Из данного равенства можно вычислить период колебаний:

Частота колебаний v является величиной, которая обратна периоду колебаний. Это количество полных колебаний, выполняемых за единицу времени:

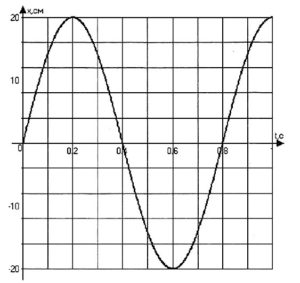
На графике изображены гармонические колебания, где а — зависимость смещения х от времени /, б — зависимость скорости vx от времени С, в — зависимость ускорения ах от времени t.

Единицей частоты в СИ является герц (Гц). Это частота периодического периода, в котором в течение 1 секунды выполняется одно полное колебание.

Можно представить, что материальная точка совершает прямолинейные гармонические колебания, относительно оси Х около равновесного положения, которое является началом отсчета координат. Так как движения частицы колебательные, ей присуще скорость и ускорение. Характеристики данного процесса будут записаны таким образом:

Смещение \(x=A\times \cos \left(\omega _<0>t+\phi _ <0>\right)\)

Скорость \(v_=\dot=-A\omega _<0>\times \sin \left(\omega _ <0>t+\phi_ <0>\right)=A\omega _<0>\times \cos \left(\omega _ <0>t+\phi_ <0>+\frac<\pi ><2>\right)\)

\(a_=\dot>=\ddot=-A\omega _<0>\times \cos \left(\omega _ <0>t+\phi_ <0>\right)=A\omega _<0>^<2>\times \cos \left(\omega _ <0>t+\phi_ <0>+\pi \right)\)

Как найти период для физического маятника

В случае, когда углы отклонения \(\varphi\) небольшие, физический маятник будет совершать гармонические колебания. Можно считать его вес, приложенным к центру тяжести в точке С. Сила возврата маятника в равновесное положение является составляющей силы тяжести — сила F:

\(F=mg\times \sin \varphi\)

Отрицательное значение правой части уравнения означает, что сила F ориентирована по направлению уменьшения угла \(\alpha\)

Учитывая малый угол \(\varphi\) уравнение можно записать в следующем виде:

С помощью основного уравнения динамики, описывающее вращательное движение, можно вывести закон движения физического маятника:

При условии невозможности определения момента силы в явном виде, дифференциальное уравнение колебаний физического маятника будет записано в такой форме:

В результате сравнения полученного выражения и уравнения гармонических колебаний, получим:

Таким образом, получается, что формула циклической частоты пружинного маятника имеет следующий вид:

В таком случае для расчета периода колебаний математического маятника будет использоваться формула:

Исходя из расчетов, можно сделать следующие выводы:

В приведенных формулах:

Примеры решений

Шариком, привязанным к нити, совершено 60 колебаний в течение 2 минут. Необходимо определить, каковы период и частота колебаний шарика.

Ответ: период колебаний маятника равен 2 секундам, а частота составляет 0,5 Гц.

Согласно изображенного графика зависимости координаты от времени, необходимо рассчитать характеристики колебательного движения тела.

\(x(t)=A\sin 2\pi Vt=0.2\sin 2\pi \times 1.25t=0.2\sin 2.5\pi t\)

Ответ: амплитуда колебаний маятника составляет 0,2 метра, период колебаний соответствует 0,8 с, частота колебаний равна 1,25 Гц, уравнение координаты будет записано в следующем виде: \(x(t)=0.2\sin 2.5\pi t\)

Необходимо определить, какой длиной обладает математический маятник, который совершает гармонические колебания при частоте 0,5 Гц на поверхности Луны. Ускорение свободного падения в данном случае составляет 1,6 м/с2.

Период колебаний математического маятника рассчитывается по формуле:

Для того чтобы выразить длину маятника, необходимо возвести обе части равенства в квадрат:

Ответ: длина математического маятника примерно составляет 0,16 метра.

Источник

Подобные системы довольно широко распространены за счет своей функциональной гибкости. Механизмы на основе таких маятников часто используются как элементы средств автоматики.

В том числе они нашли применение в контактных взрывателях различных боеприпасов, в качестве акселерометров в контурах управления ракет. Так же они активно используются в предохранительных клапанах, устанавливаемых в трубопроводах.

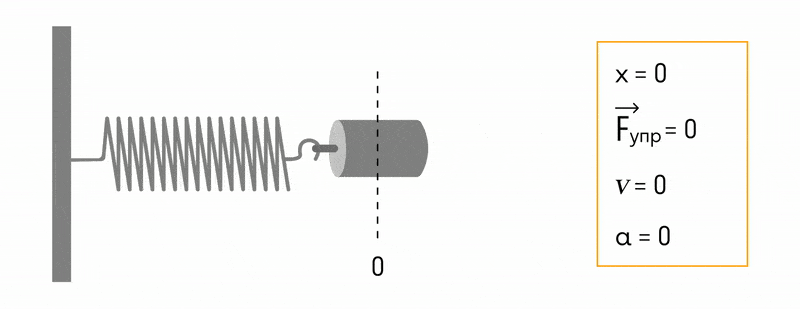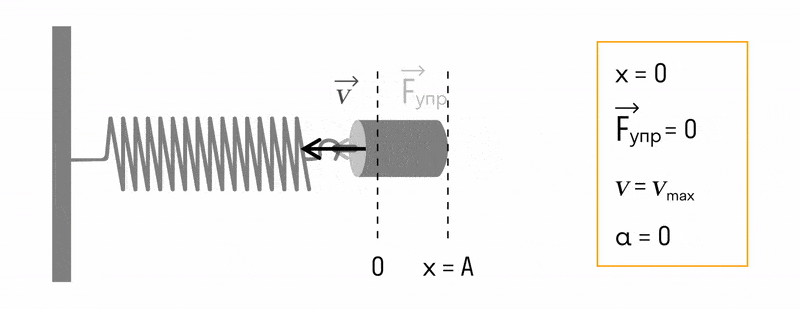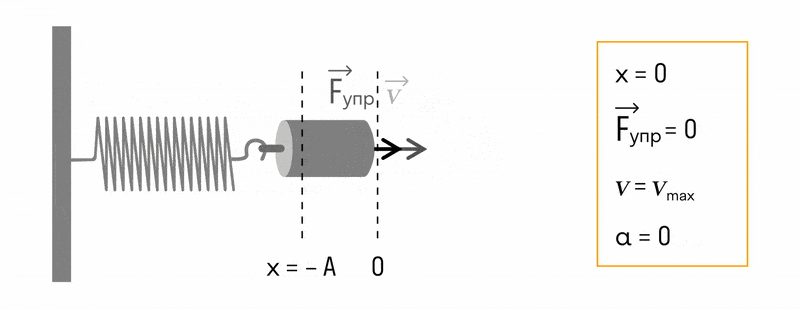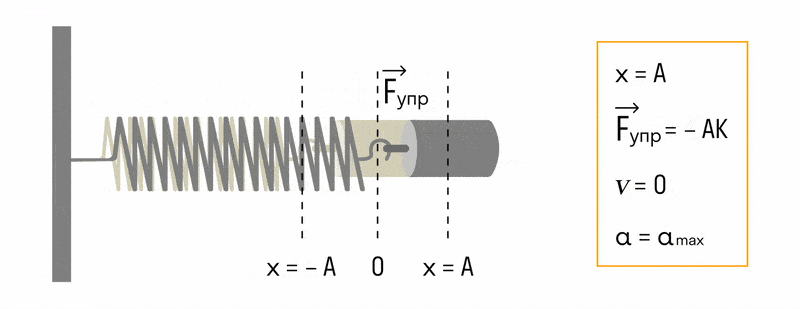
Что такое пружинный маятник

Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости.

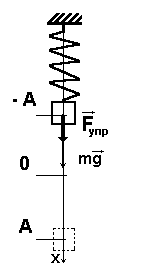
Приняты следующие обозначения:

Общий вид маятника:

Особенностями пружинных маятников являются:

Сочетание тела и пружины. Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;

У любой пружины есть исходное положение, предел сжатия и растяжения. При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;

Полная механическая энергия появляется с началом процесса обратимого деформирования. В этот момент на объект не оказывает действие сила упругости;

Колебательные движения происходят под влиянием силы упругости. Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;

От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения. Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.

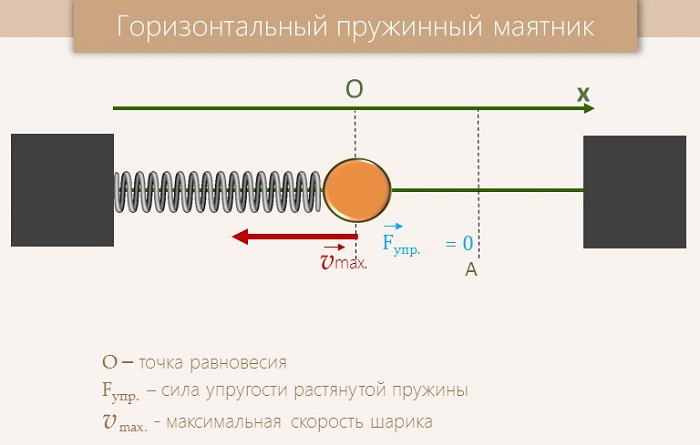
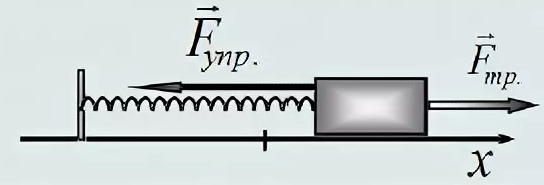
Виды пружинных маятников

Существует два типа данной системы:

Сила упругости в пружинном маятнике

До начала деформирования пружина находится в равновесном состоянии. Прикладываемое усилие может как растягивать, так и сжимать её.

Применяя к пружинному маятнику закон сохранения энергии, мы можем рассчитать силу упругости в нем. Упругость прямо пропорциональна расстоянию, на которое сместился груз.

Расчёт силы упругости может быть проведен таким образом:

где k — коэффициент жесткости пружины (Н\м),

Уравнения колебаний пружинного маятника

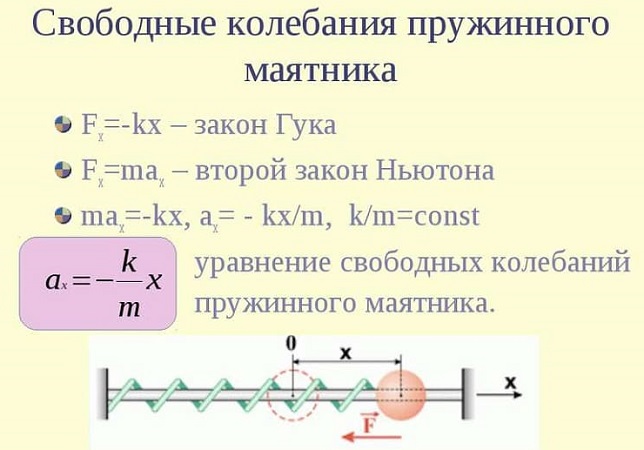
Свободные колебания пружинного маятника описываются с помощью гармонического закона.

Если допустить вероятность того, что колебания идут вдоль оси Х, и при этом выполняется закон Гука, то уравнение примет вид:

Для проведения расчета колебаний, учитывая все вероятности, применяют следующие формулы:

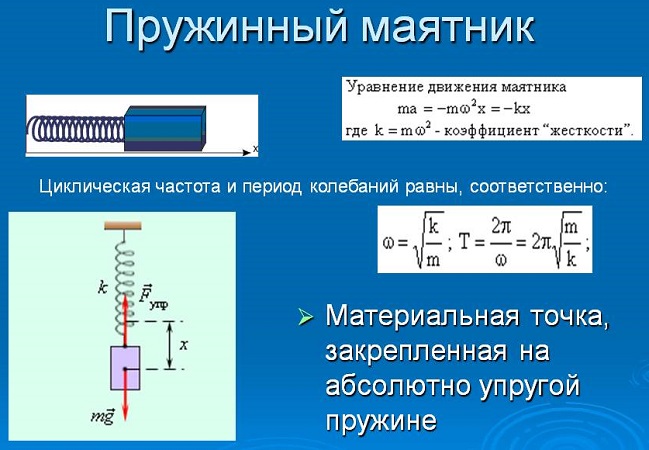
Период и частота свободных колебаний пружинного маятника

При разработке проектов всегда определяется период колебаний и их частота. Для их измерения используются известные в физике формулы.

Изменение циклической частоты покажет формула, приведенная на рисунке:

Факторы, от которых зависит частота:

Коэффициент упругости. На этот коэффициент влияет количество витков, их диаметр, расстояние между ними, длина пружины, жесткость используемого сплава и т. д.

Масса груза. От этого фактора зависит возникающая инерция и скорость перемещения.

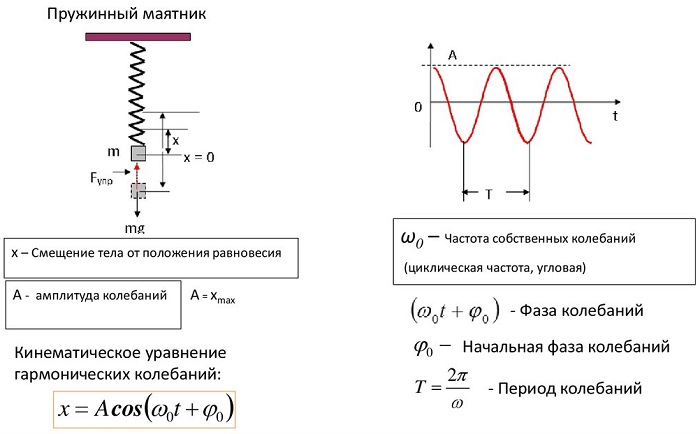
Амплитуда и начальная фаза пружинного маятника

Учитывая начальные условия и рассчитав уравнение колебаний, можем точно описать колебания пружинного маятника.

В качестве начальных условий используются: амплитуда (А) и начальная фаза колебаний (ϕ).

Энергия пружинного маятника

При рассмотрении колебания тел учитывают, что груз движется прямолинейно. Полная механическая энергия тела в каждой точке траектории является константой и равняется сумме его потенциальной энергии и кинетической энергии.

Расчет имеет особенности. При его проведении нужно учитывать несколько условий:

Колебания проходят в двух плоскостях: вертикальной и горизонтальной.

В качестве равновесного положения выбирается ноль потенциальной энергии. Находясь в этом положении пружина сохраняет свою форму.

Влияние силы трения при расчете не учитывают.

Дифференциальное уравнение гармонических колебаний пружинного маятника

Отметим, что пружинный маятник — это обобщенное определение. Скорость движения груза (тела) напрямую зависит от комплекса условий, в том числе приложенного к нему усилия.

Источник

Гармонические колебания

9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение характеризуется величинами: период, частота, амплитуда, фаза колебаний.

Формула периода колебаний

T = t/N

N — количество колебаний [-]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [-]

Она используется в уравнении гармонических колебаний:

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

2πνtв этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

g — ускорение свободного падения [м/с^2]

На планете Земля g = 9,8 м/с2

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

Рассмотрим его на примере математического маятника.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Источник

• визитки установка дверей шаблоны →