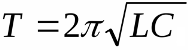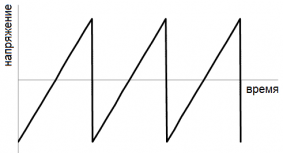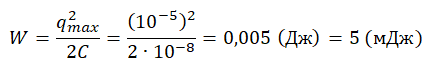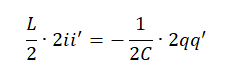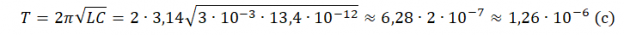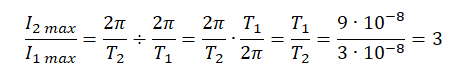Электрические колебания*

е m = С ( V 1 — V 2 ). (1)

Выражение закона Ома в данном случае будет

Если умножить уравнение (4) на С, продифференцировать его по t и сложить с уравнением (3), то получается:

Cr(di/dt) + i = — LC(d 2 i/dt)

(d 2 i/dt 2 ) + (r/L)(di/dt) + (1/LC)i = 0. (5).

Общий интеграл этого выражения будет:

Здесь A 1 и A 2 две независимые постоянные, e — основание Неперовых логарифмов, a k 1 и k 2 оба корня квадратного уравнения

Легко показать, что если k 1 и k 2 — вещественны, то при разряде ток сначала возрастает до некоторого максимума, потом непрерывно падает до нуля. Следовательно, колебаний нет. Если k 1 и k 2 мнимы, то ток, как мы сейчас увидим, есть периодическая функция времени, причем направление тока меняется. Следовательно, мы имеем колебания. Отсюда получается условие, необходимое для возможности колебаний, а именно:

Определяя коэффициенты А 1 ‘ и А 2 ‘ из начальных условий, мы можем преобразовать формулу (9) и привести ее к такому окончательному виду, где ε = √[1/( L / C ) — (r) 2 /(4 L 2 )]

Важное значение вопроса об электрических колебаниях заключается в том, что при посредстве электрических колебаний были экспериментально подтверждены воззрения Максвелла на сущность электрических явлений. Не вдаваясь в подробности (см. статьи: 1) Электричество, теория, и 2) Электромагнитная теория света), укажу в самых общих чертах основные воззрения Максвелла, сюда относящиеся. Максвелл полагает, что возможны только замкнутые токи. Следовательно, если происходит разряд конденсатора, то и тут токовые линии должны где-нибудь замкнуться. Так как это возможно только через воздух, то предположение Максвелла сводится к тому, что и в изоляторах в известных условиях возможны Э. токи. Представляя себе эфир как несжимаемую жидкость, мы можем представить себе эти токи в изоляторах как токи смещения. Эфир выводится из своего положения равновесия. Определенное количество эфира проникает внутрь поверхности проводника, и такое же количество эфира проходит наружу через поверхность другого проводника. Подобные же рассуждения применимы и к магнитному полю. Относительно магнитного поля Максвелл полагает, что его свойства не меняются от того, какого рода Э. токи происходят в нем. Совокупность электрических и магнитных изменений состояния эфира составляет «электромагнитное поле изолятора». Максвелл выразил его математически в виде шести уравнений. Из этих уравнений вытекает следующий важный результат. Если в электрических или магнитных силах произойдет какое-либо возмущение, то это возмущение распространяется в свободном эфире с конечной скоростью

v = 3 x 10 10 cm/sec

в виде поперечной волны.

v есть отношение электромагнитной и электростатической единиц количества электричества и равно скорости света. Понятно, каким образом колебания могут быть применены для опытного определения скорости распространения электромагнитных возмущений.

Для волнообразного движения существует формула

где λ — длина волны, v — скорость распространения волнообразного движения и T — период колебания.

Известно, что этот опыт был осуществлен знаменитым Герцем (см. Герца опыты).

Изложу только самые основы работ Герца. Легко понять, что если в каком-либо приборе (вибратор Герца) вызвать колебательный разряд через искру, то этот разряд вызовет в эфире возмущение, которое и будет распространяться в окружающем пространстве со скоростью

v = 3 x 10 10 cm/sec

Необходим, следовательно, прибор, который бы обнаруживал эти волны в окружающем пространстве. Таким прибором является вибратор Герца.

Устройство вибратора Герца понятно из вышеизложенных соображений. Это есть система, емкость и самоиндукция которой может быть определена, — система, заключающая в себе искровой промежуток. Герц поступал следующим образом (фиг. 1).

Винт служит для того, чтобы можно было изменять размеры искрового промежутка и по максимальной искре судить о разности потенциалов концов проволоки. Для каждого вибратора существует определенных размеров наилучший резонатор. Можно сказать, что если резонатор представляет собою почти замкнутый контур, то это будет тогда, когда длина проволоки резонатора будет равна половине длины волны, соответствующей колебанию вибратора. Тогда именно собственные колебания резонатора совпадут с колебаниями данного вибратора.

i 1 = A 1 Cos[2 π (t/T) ] + A 2 Sin[2 π (t/T) ]

Нам будет казаться, что в данном месте узел, если i = 0. Это соответствует условию: Cos[2π (t/T) ] = Cos[2 π (t — ╢)/T ]

Sin[2 π (t/T) ] = Sin[2 π (t/T) ]

Источник

Электрические колебания: виды и характеристики, амплитуда, частота и фаза колебаний

Колебания — процессы, многократно повторяющиеся или приблизительно повторяющиеся через некоторые промежутки времени. Колебательные процессы широко распространены в природе и в технике.

В электротехнике и электронике приходится иметь дело с самыми разнообразными типами электрических колебаний, т. е. колебаний напряжений и токов в различных электрических цепях, а также с механическими колебаниями, например колебаниями мембран микрофонов или громкоговорителей.

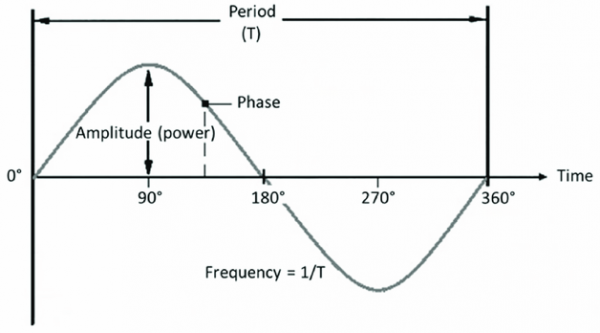
Колебания, как процессы повторяющиеся, характеризуются, во-первых, наибольшими отклонениями, которых достигает колеблющаяся величина, или амплитудой колебаний, во-вторых, частотой, с которой происходят повторения одних и тех же состояний, или частотой колебаний, и, в-третьих, тем, какое именно состояние, какая фаза процесса соответствует моменту начала отсчета времени. Эта последняя характеристика колебательного процесса называется «начальной фазой» или для краткости просто «фазой».

Характеристики колебаний (амплитуда, период, частота и фаза):

В зависимости от того, что происходит с амплитудой, различают колебания:

стационарные или незатухающие, амплитуда которых не меняется со временем ;

затухающие, амплитуда которых уменьшается со временем ;

нарастающие, амплитуда которых нарастает со временем ;

модулированные по амплитуде, амплитуда которых со временем то возрастает, то убывает.

В зависимости от того, как повторяются колебания со временем, различают колебания:

периодические, т. е такие, у которых все состояния повторяются точно через определенные промежутки времени ;

приблизительно периодические, при которых все состояния лишь приблизительно повторяются, например, затухающие или частотно-модулированные (т. е. колебания, частота которых все время изменяется в некоторых пределах около какого-то определенного значения).

синусоидальные (гармонические) или близкие к синусоидальным ;

релаксационные, форма которых существенно отличается от синусоидальных.

Наконец, по происхождению колебательного процесса различают:

собственные или свободные колебания, возникающие в результате происшедшего в системе толчка (или вообще нарушения равновесия системы) ;

вынужденные возникающие в результате длительного внешнего колебательного воздействия на систему, и автоколебания, происходящие в системе при отсутствии внешних воздействий, в силу способности самой системы поддерживать колебательный процесс в ней.

Быстрые же колебания создаются при помощи специальных методов, среди которых в современной технике наибольшую роль играют электронные генераторы.

В зависимости от частоты принято делить электрические колебания на две группы — низкой частоты, частота которых ниже 15 000 гц, и высокой частоты, частота которых больше 15 000 гц. Граница эта выбрана потому, что колебания ниже 15 000 гц производят ощущение звука в человеческом ухе, колебаний же с частотой выше 15 000 гц человеческое ухо не слышит.

Частота собственных колебаний в контуре приближенно определяется т. н. формулой Томсона:

Т. к. всякий контур обладает сопротивлением, в котором происходят потери энергии и выделяется тепло, то собственные колебания в контуре всегда будут затухающими. Иначе говоря, колебательный контур возвращается к электрическому «равновесию» в результате затухающего колебательного процесса.

Если сопротивление контура очень велико, то он представляет собой апериодический контур, в котором собственные колебания не возникают. Созданные в таком контуре начальные напряжения и токи затухают, не испытывая колебаний, а монотонно. Иначе говоря, такой контур при нарушении электрического «равновесия» апериодически (т. е. без колебаний) возвращается к положению «равновесия».

Источник

Электромагнитные колебания

теория по физике 🧲 колебания и волны

Заставить колебаться можно любую материю. Так, колебаться могут не только физические тела, состоящие из вещества, но и электромагнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между электрически заряженными частицами. Когда происходят колебания в механической системе, говорят, что тело совершает периодически повторяющиеся движения — оно отклоняется от положения равновесия то в одну, то в другую сторону. Когда происходят электромагнитные колебания, говорят, что электромагнитное поле периодически изменяется во времени, то есть его характеристики, то уменьшаются, то увеличиваются относительного некоторого среднего значения, которое является для них «положением равновесия».

Электромагнитные колебания — периодическое изменение во времени напряженности и индукции электромагнитного поля.

Напомним, что напряженность E представляет собой количественную характеристику электромагнитного поля, а индукция B — силовую. Причем электромагнитное поле — это взаимосвязанные между собой электрическое и магнитные поля. Так, проводник с током создает вокруг себя магнитное поле. Оно тем сильнее, чем выше сила тока в этом проводнике, которая напрямую зависит от напряжения в нем (или количества заряда, прошедшего через него за единицу времени). Поэтому изменения напряжения и силы тока в проводнике вызывают изменения напряженности и индукции магнитного поля. Следовательно, можно сделать вывод, что:

Электромагнитные колебания — периодические или почти периодические изменения во времени заряда, силы тока или напряжения.

Осциллограф

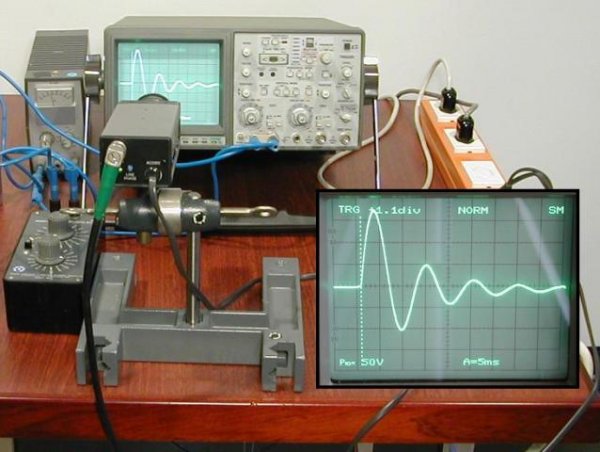
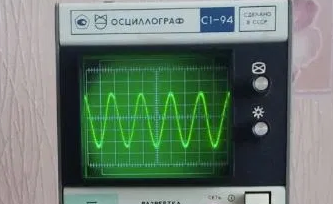
Но если колебания физических тел наблюдать легко, то колебания электромагнитного поля обнаружить без специальных приборов нельзя. Ведь увидеть изменения заряда, силы тока или напряжения невозможно. Использовать для этого электроизмерительные приборы (гальванометры, вольтметры или амперметры) тоже неудобно, поскольку электромагнитные колебания происходят с гораздо большей частотой по сравнению с механическими. Поэтому специально для визуализации электромагнитных колебаний был создан прибор, который называется осциллографом.

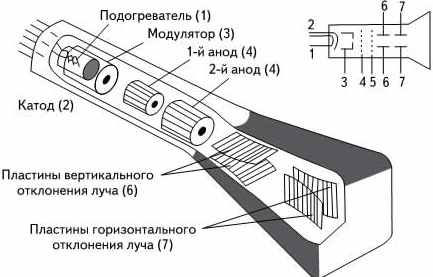
Осциллограф, схему которого вы видите ниже, представляет собой электронно-лучевую трубку. Через нее проходит узкий пучок электронов и попадает на экран, который начинает светиться при бомбардировке электронами.

На горизонтально отклоненные пластины трубки подается переменное напряжение развертки u_p пилообразной формы (см. рисунок ниже). Оно медленно нарастает и быстро падает. Поэтому электрическое поле между пластинами заставляет электронный луч пробегать экран в горизонтальном направлении с постоянной скоростью и затем почти мгновенно возвращаться назад. После этого весь процесс повторяется.

Если же присоединить вертикально отклоняющие пластины трубки к конденсатору, то колебания напряжения при его разрядке вызовут колебания луча в вертикальном направлении. В результате на экране осциллографа образуется временная развертка колебаний. Она напоминает синусоиду или косинусоиду подобно той, с помощью которой можно описать механические колебания.

С течением времени электромагнитные колебания затухают. Такие колебания являются свободными. Напомним, что свободными колебаниями называют такие колебания, которые возникают в колебательной системе после выведения ее из положения равновесия. В нашем случае система выводится из равновесия при сообщении конденсатору заряда. Зарядка конденсатора эквивалента отклонения математического маятника от положения равновесия.

В электрической цепи также можно получить вынужденные колебания, которые будут происходить до тех пор, пока на колебательную систему действует периодическая внешняя сила. Вынужденными электромагнитными колебаниями называют колебания в цепи под действием внешней периодической электродвижущей силы.

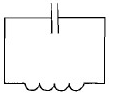
Колебательный контур

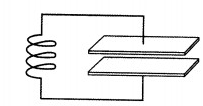
Колебательный контур — простейшая система, к которой могут происходить свободные электромагнитные колебания.

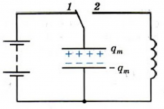
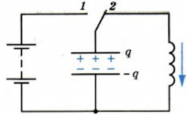
Колебательный контур состоит из конденсатора и катушки, присоединенной к его обкладкам (см. рисунок выше). Попробуем выяснить, почему в этом контуре возникают электромагнитные колебания. Для этого зарядим конденсатор, присоединив его на некоторое время к батарее с помощью переключателя (см. схему ниже).

При этом конденсатор получит энергию, равную:

Теперь переведем переключатель в положение 2 (см. схему ниже). После этого конденсатор начнет разряжаться, и в цепи появится электрический ток. Сила тока достигнет максимального значения не сразу, а будет увеличиваться постепенно. Это объясняется явлением самоиндукции. При появлении тока возникает переменное магнитное поле. Это переменное магнитное поле порождает вихревое электрическое поле в проводнике. Вихревое электрическое поле при возрастании магнитного поля действует против тока и препятствует его мгновенному увеличению.

По мере разрядки конденсатора энергия электрического поля уменьшается, но одновременно возрастает энергия магнитного поля тока, которая определяется формулой:

где i — сила переменного тока, L — индуктивность катушки.

Полная энергия W электромагнитного контура равна сумме энергий магнитного и электрического полей:

В момент, когда конденсатор полностью разрядится (q = 0), энергия электрического поля станет равной нулю. Но согласно закону сохранения энергии, максимальное значение обретет энергия магнитного поля. Сила тока в этот момент примет максимальное значение I_max.

К этому моменту разность потенциалов на концах катушки становится равной нулю. Но, несмотря на это, электрический ток не может исчезнуть сразу. Этому снова препятствует явление самоиндукции. Как только сила тока и созданное им магнитное поле начнут уменьшаться, возникает вихревое электрическое поле, которое поддерживает ток.

Конденсатор будет перезаряжаться до тех пор, пока сила тока, постепенно уменьшаясь, не станет равной нулю. Энергия магнитного поля в этот момент тоже будет равна нулю, а энергия электрического поля конденсатора опять будет максимальной. После этого конденсатор снова начнет перезаряжаться, и система вернется в исходное состояние.

Из-за частичных потерь энергии электромагнитные колебания являются затухающими. Если бы потерь не было, полная энергия система была бы постоянной и была бы равной:

Пример №1. После того как конденсатору колебательного контура был сообщен заряд q = 10 –5 Кл, в контуре возникли затухающие колебания. Какое количество теплоты выделится в контуре к тому времени, когда колебания в нем полностью затухнут? Емкость конденсатора C = 0,01 мкФ.

Поскольку с каждым колебанием колебательный контур теряет часть энергии в виде выделения тепла, ко времени, когда колебания полностью затухнут, выделится полная электромагнитная энергия системы. Ее можно определить формулой:

Сходство электромагнитных колебаний в контуре со свободными механическими колебаниями

Электромагнитные колебания в контуре имеют сходство со свободными механическими колебаниями (к примеру, колебаниями тела, закрепленного на пружине). Сходство относится не к природе самих величин, которые периодически изменяются, а к процессам периодического изменения различных величин.

Соответствие между механическими и электрическими величинами при колебательных процессах

Уравнение, описывающее процессы в колебательном контуре

Рассмотрим колебательный контур, сопротивлением R которого можно пренебречь (см. схему ниже).

Полная электромагнитная энергия равна сумме энергий магнитного и электрического полей:

Если его сопротивление равно 0, то полная механическая энергия с течением времени не меняется. А производная константы равна нулю. Следовательно, сумма производных от каждой составляющей этой энергии также равна нулю.

Первая производная по времени характеризует скорость изменения физической величины. Следовательно, эта формула позволяет сделать вывод о том, что скорость изменения энергии магнитного поля равна скорости изменения электрического поля. Знак «минус» указывает на то, что, когда энергия электрического поля возрастает, энергия магнитного поля уменьшается (и наоборот).

Вычислив обе производные, получим:

Но производная заряда по времени представляет собой силу тока в данный момент времени:

Поэтому мы можем записать уравнение иначе:

Производная силы тока по времени представляет собой вторую производную заряда по времени:

Подставив это равенство в уравнение, и преобразовав его путем деления на величину Li, получим основное уравнение, описывающее свободные электрические колебания в контуре:

Формула Томсона

Следовательно, период свободных колебаний в контуре равен:

Эта формула называется формулой Томсона.

Пример №2. Колебательный контур состоит из катушки индуктивностью L = 0,003 Гн и плоского конденсатора емкостью C = 13,4 пФ. Определите период свободных колебаний в контуре.

13,4 пФ = 13,4∙10 –12 Ф

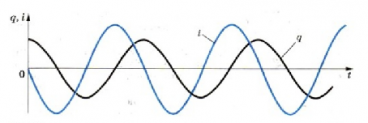
Гармонические колебания заряда и тока

Заряд конденсатора меняется с течением времени подобно тому, как координата при механических колебаниях изменяется со временем по гармоническому закону (в случае, когда в начальный момент времени отклонение от положения равновесия максимально):

где q m a x — амплитуда колебаний заряда.

Сила тока также совершает гармонические колебания:

где I m a x — амплитуда колебаний силы тока, равная произведению циклической частоты на амплитуду колебаний заряда:

I m a x = q m a x ω 0

Пример №3. В двух идеальных колебательных контурах с одинаковой индуктивностью происходят свободные электромагнитные колебания, причём период колебаний в первом контуре 9⋅10 −8 с, во втором 3⋅10 −8 с. Во сколько раз амплитудное значение силы тока во втором контуре больше, чем в первом, если максимальный заряд конденсаторов в обоих случаях одинаков?

Максимальная сила тока равна:

I m a x = q m a x ω 0

Так как максимальный заряд конденсаторов одинаков в обоих контурах, отношение силы тока во тором контуре к силе ток в первом контуре равно:

Циклическую частоту выразим из формулы Томсона:

Автоколебания

Незатухающие вынужденные колебания поддерживаются в цепи действием внешнего периодического напряжения. Но существует способ создания незатухающих колебаний, при котором колебательная система сама регулирует поступление энергии в колебательный контур для компенсации потерь энергии на резисторе.

Автоколебательные системы — системы, в которых генерируются незатухающие колебания за счет поступления энергии от источника тока внутри системы.

Автоколебания — незатухающие колебания, существующие в системе без воздействия на нее внешних периодических сил.

Самый простой пример автоколебательной системы — это генератор на транзисторе. Транзистор представляет собой полупроводниковое устройство, состоящее из эмиттера, базы и коллектора и имеющее 2 p–n перехода. Колебания тока в контуре вызывают колебания напряжения между эмиттером и базой, которые, в свою очередь, управляют силой тока в цепи колебательного контура (обратная связь). От источника напряжения в контур поступает энергия, компенсирующая потери энергии в контуре на транзисторе.

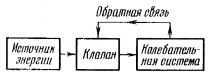
Схема автоколебательной системы представлена ниже.

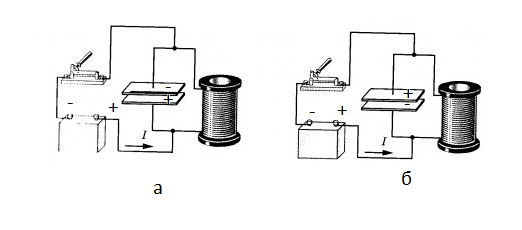
Преимуществом такой схемы является то, что конденсатор при этом подключается к источнику тока только тогда, когда присоединенная к положительному источнику тока пластина конденсатора заряжена положительно (рис. а). Только в этом случае конденсатор восполняет потери энергии, выделенной на резисторе.

Если бы источник тока был включен всегда, восполнения потерь не происходило бы. Поскольку конденсатор разряжался бы в момент, когда он соединен с источником тока пластиной, заряженной отрицательно (рис. б).

В двух идеальных колебательных контурах происходят незатухающие электромагнитные колебания. Максимальное значение заряда конденсатора во втором контуре равно 6 мкКл. Амплитуда колебаний силы тока в первом контуре в 2 раза меньше, а период его колебаний в 3 раза меньше, чем во втором контуре. Определите максимальное значение заряда конденсатора в первом контуре.

Источник

Электрические колебания (определение частоты)

Электрическими колебаниями называются любые периодически повторяющиеся изменения электрических величин в цепи: напряжения, силы тока или напряженностей электрического и магнитного полей и т. п. В данном, частном случае рассматриваются электрические колебания (их часто называют также и электромагнитными колебаниями), происходящие в колебательном контуре, состоящем из катушки индуктивности и конденсатора (рис.).

Что такое электрические колебания

При свободных колебаниях в контуре происходит периодически повторяющийся процесс перехода электрического поля конденсатора в магнитное поле катушки и обратно через посредство образующегося при этом в контуре переменного тока.

Рассмотрим явления, происходящие в идеальном колебательном контуре (т. е. в контуре, не имеющем активного сопротивления) с момента, когда конденсатор контура заряжен от постороннего источника напряжения (затем этот источник удален).

В начальный момент времени конденсатор заряжен, в нем образовалось электрическое поле, напряжение на нем U_к максимально, ток I_к в контуре равен нулю (рис., а = 1). В следующий момент конденсатор начинает разряжаться, напряжение U_K на его зажимах падает, в контуре появляется ток, постепенно возрастающий по величине.

Проходя по виткам, ток образует магнитное поле, и в катушке появляется электродвижущая сила самоиндукции E_l, замедляющая нарастание тока (рис., а = 2). По мере приближения мгновенных значений тока I_к к максимальной величине I_т электродвижущая сила самоиндукции E_L уменьшается и при I_к = I_m, т. е- в момент, когда нарастание тока прекращается, она обращается в нуль (рис., а = 3). Конденсатор к этому моменту разряжается и напряжение U_K снижается до нуля.

При этом ток I_к начинает убывать, что вызывает появление в катушке э. д. с. самоиндукции обратного знака, которая поддерживает ток в контуре за счет энергии постепенно ослабляющегося магнитного поля (рис., а = 4). Под действием тока конденсатор вновь заряжается, но с обратным знаком полярности пластин. К моменту, когда ток постепенно снизится до нуля, конденсатор полностью заряжен, но с обратной исходному положению полярностью пластин (рис., а-5).

Затем процесс повторяется, но ток I_к протекает в контуре в обратном направлении (рис., б), так проходит один период колебательного процесса.

Как показывает теория этого вопроса, изменение во времени величин, обусловливающих колебательный процесс: U_K, I_к и E_l, происходит по законам гармонического колебания, т. е. имеет синусоидальный характер. Это относится также и к колебаниям напряженностей Е электрического поля конденсатора и Н магнитного поля катушки. При этом как колебания тока I_к в контуре по отношению к напряжению U_K на зажимах конденсатора, так и колебания напряженности Н магнитного поля в катушке по отношению к напряженности Е электрического поля в конденсаторе запаздывают по фазе на угол 90°.

Свободные электрические колебания

Свободные электрические колебания в идеальном контуре являются незатухающими. В реальном контуре, где, кроме индуктивности и емкости, имеется активное сопротивление, происходит потеря энергии. В связи с этим амплитуды напряжения на зажимах конденсатора и соответственно тока в контуре с каждым последующим колебанием уменьшаются и колебания являются затухающими.

На рис. 2, а показан опыт (на рис. 2, б — принципиальная схема) возбуждения в контуре затухающих электрических колебаний.

Колебательный контур состоит из катушки L и конденсатора С с достаточно большими индуктивностью и емкостью. В контур последовательно включен гальванометр с нулем посредине шкалы. С помощью двойного ключа К конденсатор С контура сначала подключается к батарее Б (при этом конденсатор заряжается), а затем к катушке L, вместе с которой он образует колебательный контур. При этом в контуре возникает серия затухающих колебаний, наблюдаемых по отклонениям стрелки призора.

Период электрических колебаний зависит от емкости и индуктивности контура. Чем больше индуктивность катушки, тем медленнее происходит нарастание и снижение тока в ней, и чем больше емкость конденсатора, тем медленнее происходят его заряд и разряд при прочих равных условиях.

Определение частоты колебаний

Частоту колебаний в контуре можно определить из условия, численного равенства напряжения U_K на зажимах конденсатора и падения напряжения I_kxl на катушке:

Генератор электрических колебаний

Для того чтобы обеспечить незатухающие колебания, особенно в тех случаях, когда мощность их используется для каких-либо полезных целей, необходимо пополнять энергию, расходуемую в контуре с помощью соответствующего источника питания.

Простейший генератор незатухающих электрических колебаний (рис. 3) состоит из колебательного контура (катушка индуктивности L и конденсатор С), который включен в анодную цепь трехэлектродной лампы Л последовательно с источником Б постоянного напряжения. С катушкой L контура индуктивно связывается катушка К, концы которой подключены к сетке и катоду лампы. Она связывает работу лампы Л с колебательным процессом в контуре и называется катушкой обратной связи, а весь генератор — генератором с трансформаторной обратной связью. Генератор представляет собой автоколебательную систему, в которой поддерживается незатухающие колебания и обеспечивается их самовозбуждение.

Незатухающие колебания получаются благодаря периодической подзарядке конденсатора анодным током лампы, проходящим через контур.

При этом амплитудные значения напряжения на зажимах конденсатора поддерживаются на постоянном уровне, а энергия, расходуемая в контуре, пополняется за счет источника питания в анодной цепи лампы.

Для того чтобы осуществлять периодическую подзарядку конденсатора контура в необходимые моменты, анодный ток должен иметь пульсирующий характер. Это обеспечивается путем соответствующего изменения потенциала на сетке лампы, который создается через посредство катушки К связи самим колебательным процессом.

Как работает самовозбуждение в генераторе

Рассмотрим самовозбуждение колебаний в генераторе (рис. 3, а). При замыкании ключа В (потенциалы на сетке и на катоде в этот момент равны) в цепи проходит ток покоя лампы, который в контуре разветвляется между катушкой L и конденсатором С. Конденсатор при этом начинает заряжаться, а в катушке возбуждается э. д. с. самоиндукции, замедляющая нарастание тока.

При этом в катушке связи наводится э. д. с. индукции, которая образует на сетке лампы положительный потенциал (для этого катушка К подключается к сетке и катоду определенными концами; в противном случае на сетке будет отрицательный потенциал и самовозбуждения колебаний не произойдет). В связи с образованием положительного потенциала на сетке анодный ток лампы, проходящий через контур, продолжает нарастать до наибольшей величины — тока насыщения. Конденсатор контура при этом заряжается до максимального напряжения.

В момент достижения током максимальной величины индукция в катушке связи прекращается и потенциал на сетке лампы снижается до нуля, что вызывает уменьшение тока, проходящего через контур. В катушке связи при этом наводится э. д. с. индукции обратного знака, сообщающая сетке отрицательный потенциал, и ток в цепи снижается еще больше, вплоть до некоторого минимального значения. Тогда конденсатор начинает разряжаться через катушку и в контуре возникают электрические колебания, частота которых обусловливается емкостью и индуктивностью контура.

При установившемся колебательном процессе ток I_к, проходящий по катушке контура, индуктирует через катушку связи на сетке лампы переменный, потенциал U_c (см. график на рис. 3, б), который вызывает соот ветствующие колебания анодного тока. Анодный ток I_а имеет пульсирующий характер и рассматривается как состоящий из двух токов: постоянного I_а0 и накладывающегося на него переменного I

частота которого соответствует частоте колебательного процесса (рис 3, б). Постоянная составляющая анодного тока проходит через катушку контура и на колебательный процесс влияния не оказывает. Переменная составляющая анодного тока проходит преимущественно через конденсатор, представляющий для нее значительно меньшее сопротивление, чем катушка, и, складываясь с током колебательного процесса, подзаряжает конденсатор.

Подзарядка конденсатора, при которой происходит передача энергии от источника питания в колебательный контур, имеет место только в положительные полупериоды колебаний анодного тока, когда мгновенные значения его превышают величину постоянной составляющей, т. е. один раз за период колебательного процесса. В связи с этим генератор называется простым или однотактным.

В рассмотренном генераторе источник питания включается последовательно в цепь лампы (генератор с последовательным питанием). На практике-чаще применяется параллельное питание. В этом генераторе, принцип работы которого полностью аналогичен предыдущему, постоянная и переменная составляющие анодного тока разделяются благодаря наличию в схеме фильтровых элементов: дросселя L_p и конденсатора С_р. Постоянная составляющая проходит через дроссель и источник питания, переменная — через разделительный конденсатор и колебательный контур.

Имеются генераторы с автотрансформаторной обратной связью. При этом потенциал на сетку лампы подается непосредственно от части витков катушки контура, начальная точка которых включена к катоду, конечная — к сетке лампы (этим обеспечивается необходимый для самовозбуждения генератора знак потенциала на сетке).

Применение генераторов электрических колебаний

Применяются также генераторы электрических колебаний с независимым возбуждением. В этом случае колебания от независимого источника Г, называемого возбудителем, подаются на сетку лампы Л, в анодную цепь которой включен основной колебательный контур LC генератора. Колебания потенциала на сетке вызывают соответствующие колебания анодного тока лампы, который, проходя через колебательный контур, вызывает и поддерживает в нем колебания с частотой, равной или кратной частоте возбудителя.

Для точной настройки контура на необходимую частоту в него включается регулировочный конденсатор (что на схемах обозначается пересекающей его стрелкой). Генератор с независимым возбуждением можно рассматривать как усилитель колебаний, поданных на сетку, с настроенным контуром в цепи анода.

В генераторах электрических колебаний, кроме триодов, используются также лампы с двумя и тремя сетками (тетроды и пентоды), что улучшает рабочие характеристики генератора и повышает его мощность. В генераторах также применяется подача на сетку лампы напряжения смешения. Эти вопросы в какой-то мере были затронуты выше применительно к усилителю колебаний. В настоящее время все элементы схемы заменены на новую схему (микросхема генератор и полевые транзисторы).

Статья на тему Электрические колебания

Похожие страницы:

Понравилась статья поделись ей

Источник