Что называется угловым коэффициентом функции в данной точке
Угловой коэффициент прямой
Угловой коэффициент прямой — коэффициент 

Тангенс угла может рассчитываться как отношение противолежащего катета к прилежащему. k всегда равен 
При положительных значениях углового коэффициента k и нулевом значении коэффициента сдвига b прямая будет лежать в первом и третьем квадрантах (в которых x и y одновременно положительны и отрицательны). При этом большим значениям углового коэффициента k будет соответствовать более крутая прямая, а меньшим — более пологая.
Прямые 



Примечания
Полезное
Смотреть что такое «Угловой коэффициент прямой» в других словарях:
угловой коэффициент (прямой) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN slope … Справочник технического переводчика
Угловой коэффициент — (математическое) число k в уравнении прямой линии на плоскости у = kx+b (см. Аналитическая геометрия), характеризующее наклон прямой относительно оси абсцисс. В прямоугольной системе координат У. к. k = tg φ, где φ угол между… … Большая советская энциклопедия
Уравнения прямой — Изображение прямых в прямоугольной системе координат Прямая одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется… … Википедия
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ — раздел геометрии, который исследует простейшие геометрические объекты средствами элементарной алгебры на основе метода координат. Создание аналитической геометрии обычно приписывают Р.Декарту, изложившему ее основы в последней главе своего… … Энциклопедия Кольера
Время реакции (reaction time) — Измерение времени реакции (ВР), вероятно, самый почтенный предмет в эмпирической психологии. Оно зародилось в области астрономии, в 1823 г., с измерением индивидуальных различий в скорости восприятия пересечения звездой линии риски телескопа. Эти … Психологическая энциклопедия
МАТЕМАТИЧЕСКИЙ АНАЛИЗ — раздел математики, дающий методы количественного исследования разных процессов изменения; занимается изучением скорости изменения (дифференциальное исчисление) и определением длин кривых, площадей и объемов фигур, ограниченных кривыми контурами и … Энциклопедия Кольера
Прямая — У этого термина существуют и другие значения, см. Прямая (значения). Прямая одно из основных понятий геометрии, то есть точного универсального определения не имеет. При систематическом изложении геометрии прямая линия обычно принимается за одно… … Википедия
Прямая линия — Изображение прямых в прямоугольной системе координат Прямая одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется… … Википедия
Прямые — Изображение прямых в прямоугольной системе координат Прямая одно из основных понятий геометрии. При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется… … Википедия
Малая полуось — Не следует путать с термином «Эллипсис». Эллипс и его фокусы Эллипс (др. греч. ἔλλειψις недостаток, в смысле недостатка эксцентриситета до 1) геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний от двух данных точек F1… … Википедия
Угловой коэффициент.
Угловой коэффициент— коэффициент k в уравнении прямой на плоскости y = kx + b. Он численно равняется тангенсу угла между выбранной прямой и осью 0х. Этот угол отсчитывается от положительного направления оси 0х до прямой против хода часовой стрелки и располагается и пределах от 0 до 180 градусов.
Для обозначения углового коэффициента употребляют латинский символ k. И, основываясь на определении получаем:
Когда прямая параллельна оси 0х или совпадает с ней, то угол ее наклона расценивают, как равный нулю.
Когда прямая параллельна оси 0у, то угловой коэффициент отсутствует и принято указывать, что угловой коэффициент обращается в бесконечность.
Положительный угловой коэффициент прямой свидетельствует о росте графика функции, отрицательный угловой коэффициент – об убывании.
Угловой коэффициент прямой так же есть возможность вычислить, когда установлены координаты двух произвольных точек прямой:
Тогда, в образовавшемся прямоугольном треугольнике M1РM2 вычисляем тангенс:
Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач
Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Угол наклона прямой и угловой коэффициент прямой
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.
Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Уравнение с угловым коэффициентом
Ответ: М 1 принадлежит прямой, а М 2 нет.
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Решение
Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
Решим задачу обратную данной.
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
График линейной функции, его свойства и формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
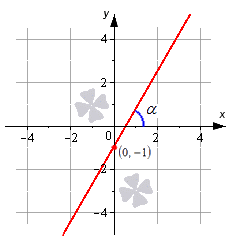
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!
Свойства линейной функции
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
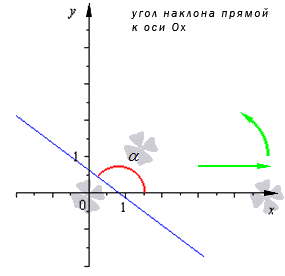
На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.
Получаем формулу для нахождения секущей вида:
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.
Решение
Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3
Отсюда следует, что α x = a r c t g 3 3 = π 6
Ответ: уравнение касательной приобретает вид
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
Для наглядности изобразим графически.
Решение
Необходимо продифференцировать функцию. Имеем, что
Вычисляем соответствующие значения функции
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
Другое уравнение имеет два действительных корня, тогда
Перейдем к нахождению значений функции. Получаем, что
Возможно существование бесконечного количества касательных для заданных функций.
Решение
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у :
Ответ: необходимы уравнения запишутся как
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Данное равенство может быть записано как объединение двух функций:
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Касательная к эллипсу
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
Решение
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид
Графически касательные обозначаются так:
Касательная к гиперболе
Гипербола может быть представлена в виде двух объединенных функций вида
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
Ответ: уравнение касательной можно представить как
Наглядно изображается так:
Касательная к параболе
Графически изобразим как:
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.
Отсюда определим значение х для точек касания.
Первая функция запишется как
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.
Вторая функция запишется как
Ответ: уравнение касательной принимает вид