Что называется таблицей истинности
Что называется таблицей истинности
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Таблица истинности
Что такое таблицы истинности
Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для создания таблиц истинности используются обозначения логических значений 0 (ложь) и 1 (истина).
Можно встретить вариацию таблицы, в которой число столбцов равно n + число используемых логических операций. В подобной таблице в первые n столбцы, так же как и в первом варианте, вписаны наборы аргументов, а остальные столбцы заполнены значениями подфункций, которые входят в запись функции. Благодаря этим промежуточным вычислениям, упрощается расчет конечного значения функции.
Применение таблиц истинности чаще всего встречается в булевой алгебре и в цифровой электронной технике для описания работы логических схем.
Логические операции
Логические операции — построение из одного или нескольких высказываний нового высказывания.
Результатом может являться не только образование нового высказывания, но и изменение содержания или объема уже данных высказываний. В случае логической операции истинность значения нового высказывания всецело определяется истинностью значения исходных высказываний.
К логическим операциям относятся конъюнкция, дизъюнкция, импликация, разделительная дизъюнкция, эквиваленция, антиконъюнкция, антидизъюнкция.
Логические выражения
Логическое выражение — это запись, принимающая логическое значение «истина» или «ложь».
Их можно разделить на два типа:
Инверсия или логическое отрицание — это логическая операция, при выполнении которой из данного высказывания получается новое высказывание. Это высказывание является отрицанием исходного высказывания.
Унарной в данном случае называется операция, которая используется относительно одной величины.
Конъюнкция
Конъюнкция — это логическое умножение. Эта операция, для которой требуются два и более логических величины. Конъюнкция соединяет логические высказывания при помощи связки «и». Связка изображается символом ∧.
Конъюнкция может быть истинной только в том случае, если оба высказывания истинны. Например, A ∧ B, если A = ложь, а B = истина, является ложным.
Дизъюнкция
Дизъюнкция — логическое сложение. Эта логическая операция соединяет два и более высказываний с помощью связки «или». Эта связка обозначается как ∨.
Логическое высказывание будет истинным, если истинно хотя бы одно из условий. Например, A ∨ B истинно, даже если А = истина, а В = ложь. Высказывание будет ложным только в том случае, если ложны и А, и В.
Правила составления таблицы истинности
Таблицу истинности можно построить для любого логического выражения. В этой таблице будут отражены все значения, которые принимает выражение при всех наборах значений входящих в него переменных.
Строить таблицы истинности необходимо по следующему алгоритму:
Примеры построения таблицы истинности
Задача
Решение
| А | В | \(А \vee В\) | ¬А | ¬В | \(¬А \vee ¬В\) | \((A \vee B) \wedge (¬A \vee ¬B)\) |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
После заполнения таблицы, ответ будет выглядеть следующим образом:
F = 0 при A = B = 0 и A = B = 1
Задача
Построим еще одну таблицу истинности и решим выражение \(F = X \vee Y \wedge ¬Z\)
Решение
| X | Y | Z | ¬ Z | \(Y \wedge ¬Z\) | \(X \vee Y \wedge ¬Z\) |
| 0 | 0 | 0 | q | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 |
После заполнения таблицы, ответ будет выглядеть следующим образом:
F = 0, при X = Y = Z = 0; при X = Y = 0 и Z = 1.
таблица истинности
Полезное
Смотреть что такое «таблица истинности» в других словарях:
Таблица истинности — Таблица истинности это таблица, описывающая логическую функцию. Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность.… … Википедия
таблица истинности — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN truth table … Справочник технического переводчика
таблица истинности — teisingumo lentelė statusas T sritis automatika atitikmenys: angl. Boolean operation table; truth diagram; truth table vok. Wahrheitstabelle, f rus. таблица истинности, f pranc. table de vérité, f … Automatikos terminų žodynas
таблица истинности (двоичной функции) — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index&d=4885] Тематики защита информации EN truth table … Справочник технического переводчика
ИСТИННОСТИ ТАБЛИЦА — ИСТИННОСТИ ТАБЛИЦА см. Логика высказываний. Новая философская энциклопедия: В 4 тт. М.: Мысль. Под редакцией В. С. Стёпина. 2001 … Философская энциклопедия
диаграмма истинности — таблица истинности — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы таблица истинности EN truth diagram … Справочник технического переводчика
Карта Карно — Рис. 1 Пример Куба Карно Куб Карно графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного… … Википедия
ЭЛЕКТРОННЫЕ СХЕМЫ — графические изображения и элементы многочисленных и разнообразных приборов и устройств электроники, автоматики, радио и вычислительной техники. Проектирование и разработка базовых электронных схем и создаваемых из них более сложных систем как раз … Энциклопедия Кольера
Урок информатики по теме «Основы логики, таблицы истинности»
Продолжительность урока: 45 мин
Ход урока
I. Организационный момент
Мы продолжаем изучение темы “Основы логики”. На предыдущих уроках мы увидели, что логика достаточно крепко связана с нашей повседневной жизнью, а также увидели, что почти любое высказывание можно записать в виде формулы.
II. Повторение материала предыдущего урока
Давайте вспомним основные определения и понятия:
| Вопрос | Ответ |
| 1. Какое предложение является высказыванием? | Повествовательное предложение, в котором что-либо утверждается или отрицается |
| 2. На какие виды делятся высказывания по своей структуре? | Простые и сложные |
| 3. Истинность каких высказываний является договорной? | Простых |
| 4. Истинность каких высказываний вычисляется? | Сложных |
| 5. Как обозначаются простые высказывания в алгебре высказываний? | Логическими переменными |
| 6. Как обозначается истинность таких высказываний? | 1 и 0 |
| 7. Что связывает переменные в формулах алгебры высказываний? | Логические операции |
| 8. Перечислите их. | Инверсия (отрицание) |
Эквиваленция (равносильность)
III. Объяснение нового материала
Последние два примера относятся к сложным высказываниям. Как же определить истинность сложных высказываний?
Мы говорили, что она вычисляется. Для этого в логике существуют таблицы для вычисления истинности составных (сложных) высказываний. Они называются таблицами истинности.
Итак, тема урока ТАБЛИЦЫ ИСТИННОСТИ.
(Далее вся работа происходит за компьютерами: учащиеся садятся за компьютеры и запускают демонстрацию урока “Таблицы истинности” (Приложение 1.pps))
3.1) Определение. Таблица истинности – это таблица, показывающая истинность сложного высказывания при всех возможных значениях входящих переменных (Рисунок 1).
3.2) Разберем подробнее каждую логическую операцию в соответствии с ее определением:
1. Инверсия (отрицание) – это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
Эта операция относится только к одной переменной, поэтому для нее отведено только две строки, т.к. одна переменная может иметь одно из двух значений: 0 или 1.
2. Конъюнкция (умножение)– это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Легко увидеть, что данная таблица действительно похожа на таблицу умножения.
3. Дизъюнкция (сложение) – это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Можно убедиться, что таблица похожа на таблицу сложения кроме последнего действия. В двоичной системе счисления 1 + 1 = 10, в десятичной – 1 + 1 = 2. В логике значения переменной 2 невозможно, рассмотрим 10 с точки зрения логики: 1 – истинно, 0 – ложно, т.о. 10 – истинно и ложно одновременно, чего быть не может, поэтому последнее действие строго опирается на определение.
4. Импликация (следование) – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие истинное, а следствие ложно.
5. Эквиваленция (равносильность) – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или ложны.
Последние две операции были разобраны нами на предыдущем уроке.
3.4) Рассмотрим пример составления таблицы истинности для сложного высказывания:
Пример. Построить таблицу истинности для формулы: А U В —> ¬А U С.
Из примера видно, что таблицей истинности является не все решение, а только последнее действие (столбец, выделенный красным цветом).
IV. Закрепление.
Для закрепления материала вам предлагается решить самостоятельно примеры под буквами а, б, в, дополнительно г–ж (Рисунок 3).
V. Домашнее задание, обобщение материала.
Домашнее задание дано вам также на экране монитора (Рисунок 4)
Обобщение материала: сегодня на уроке мы научились определять истинность составных высказываний, но больше с математической точки зрения, так как вам были даны не сами высказывания, а формулы, отображающие их. На следующих уроках мы закрепим эти умения и постараемся их применить к решению логических задач.
Логические выражения и таблица истинности
Логические выражения и таблица истинности
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение — составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
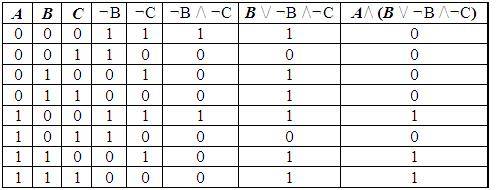
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк — 2 3 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.
1. В выражении две переменные А и В (n=2).
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.