Что называется средней скоростью перемещения кратко
Что называется средней скоростью перемещения кратко
Неравномерное движение — это движение, при котором за равные промежутки времени тело проходит разные пути.
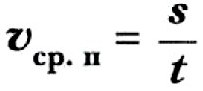
Средняя путевая скорость — это физическая величина, равная отношению пути, пройденного телом за рассматриваемый промежуток времени, к длительности этого промежутка.
Средняя путевая скорость — скалярная неотрицательная величина.
Средняя скорость тела за промежуток времени t — это физическая величина, равная отношению перемещения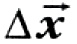 
, совершённого телом, к длительности этого промежутка времени.
Средняя скорость — вектор. Она направлена туда, куда направлено перемещение тела за рассматриваемый промежуток времени.
Если тело всё время движется в одном направлении, то модуль средней скорости равен средней путевой скорости. Если же в процессе своего движения тело меняет направление движения, то модуль средней скорости меньше средней путевой скорости.
Пример решения задач на среднюю скорость при неравномерном движении
Автомобиль проехал за первый час 50 км, а за следующие два часа он проехал 160 км. Какова его средняя скорость за все время движения?
Еще больше задач на движение (с решениями и ответами) в конспекте «Задачи на движение»
Это конспект по физике за 7 класс по теме «Неравномерное движение. Средняя скорость». Выберите дальнейшие действия:
Мгновенная и средняя скорость
Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.
Мгновенная скорость точки. Формулы
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Мгновенной скоростью называют предел, к которому стремится средняя скорость » open=» υ при стремлении промежутка времени ∆ t к 0 :
Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:
Перемещение и мгновенная скорость
Запись модуля вектора υ примет вид:
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ ( t ) d t
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения:
Средняя скорость
Всего получено оценок: 65.
Всего получено оценок: 65.
Важнейшей характеристикой тела в кинематике является скорость, с которой оно движется. Движение с нулевой скоростью фактически вообще не является движением. Однако скорость можно измерять различными методами и получать различные значения. Например, можно находить среднюю скорость. Рассмотрим эту тему подробнее: дадим определение средней скорости, приведем формулу средней скорости.
Движение и его скорость
Если движение происходит равномерно, то это отношение всегда будет одинаковым, независимо от выбора момента времени.
Рис. 1. Скорость движения.
Равномерное и неравномерное движение
Тот же автомобиль когда-то стоял на месте, затем начал разгон и лишь потом двигался равномерно. А если рассмотреть ситуацию дальше — то рано или поздно автомобиль начнет замедление и остановится.
Получается, что скорость движения в рассматриваемом промежутке времени может изменяться. Движение с изменяемой скоростью называется неравномерным.
Средняя скорость
Как можно сравнивать скорости неравномерных движений?
Один из способов решения этой задачи — использование в физике такого понятия, как средняя скорость.
Идея состоит в том, чтобы пренебречь изменением скорости во время рассматриваемого промежутка времени, а рассматривать только начальный и конечный момент. Такое измерение удобно, если нам необходимо оценить общий результат движения.
В самом деле, как правило, целью движения является прибытие в конечный пункт к необходимому моменту времени. Как именно это достигнуто, зачастую неважно. Тело могло начать движение сразу и равномерно достигнуть конечного пункта. Могло, как автомобиль, сперва разогнаться, а потом затормозить в конечном пункте к тому же моменту времени. Наконец, тело могло двигаться «рывками», делая ряд остановок во время перемещения, но прибыть в конечный пункт, опять же, к тому же моменту времени.
Во всех трех приведенных случаях важно то, что тело начало и закончило движение в одни и те же моменты и переместилось за время движения на одно и то же расстояние. Что происходило во время движения, не рассматривается.
Скорость, рассчитываемая только по начальному и конечному моменту движения, называется средней. Для нахождения средней скорости необходимо найти отношение общего перемещения материальной точки ко времени, за которое это перемещение произошло.
Например, если автомобиль начал разгон в нулевой момент времени с нулевой скорости, разогнался до 50 км/ч, потом притормозил до 40 км/ч, и потом, через минуту, остановился в 600 м от начального пункта, то для нахождения средней скорости его движения необходимо 600 м поделить на 60 с. Средняя скорость составит 10 м/с.
Рис. 3. Средняя скорость.
Что мы узнали?
Одним из способов оценки скорости неравномерного движения является средняя скорость. При расчете средней скорости исходят только из начального и конечного моментов движения. А изменениями скорости между этими моментами пренебрегают. Средняя скорость удобна, если необходимо оценить общий результат движения, не обращая внимания на мелкие детали.
Что называется средней скоростью перемещения кратко
Какую скорость показывает спидометр?
Может ли городской транспорт двигаться равномерно и прямолинейно?
Реальные тела (человек, автомобиль, ракета, теплоход и т. д.), как правило, не движутся с постоянной скоростью. Они начинают двигаться из состояния покоя, и их скорость увеличивается постепенно, при остановке скорость уменьшается также постепенно, таким образом, реальные тела движутся неравномерно.
Неравномерное движение может быть как прямолинейным, так и криволинейным.
Чтобы полностью описать неравномерное движение точки, надо знать её положение и скорость в каждый момент времени.
Скорость точки в данный момент времени называется мгновенной скоростью.
Что же понимают под мгновенной скоростью?
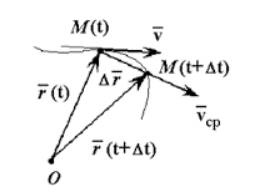
Пусть точка, двигаясь неравномерно и по кривой линии, в некоторый момент времени t занимает положение М (рис. 1.24). По прошествии времени Δt1 от этого момента точка займёт положение М1, совершив перемещение Δ
1. Поделив вектор Δ1 на промежуток времени Δt1 найдём такую скорость равномерного прямолинейного движения, с которой должна была бы двигаться точка, чтобы за время Δt попасть из положения М в положение М1. Эту скорость называют средней скоростью перемещения точки за время Δt1.
Обозначив её через 
ср1, запишем: 
Средняя скорость направлена вдоль секущей ММ1. По той же формуле мы находим скорость точки при равномерном прямолинейном движении.
Скорость, с которой должна равномерно и прямолинейно двигаться точка, чтобы попасть из начального положения в конечное за определённый промежуток времени, называется средней скоростью перемещения.
Для того чтобы определить скорость в данный момент времени, когда точка занимает положение М, найдём средние скорости за всё меньшие и меньшие промежутки времени: 
Интересно, верно ли следующее определение мгновенной скорости: «Скорость тела в данной точке траектории называется мгновенной скоростью»?
При уменьшении промежутка времени Δt перемещения точки уменьшаются по модулю и меняются по направлению. Соответственно этому средние скорости также меняются как по модулю, так и по направлению. Но по мере приближения промежутка времени Δt к нулю средние скорости всё меньше и меньше будут отличаться друг от друга. А это означает, что при стремлении промежутка времени Δt к нулю отношение 
стремится к определённому вектору как к своему предельному значению. В механике такую величину называют скоростью точки в данный момент времени или просто мгновенной скоростью и обозначают
Мгновенная скорость точки есть величина, равная пределу отношения перемещения Δ к промежутку времени Δt, в течение которого это перемещение произошло, при стремлении промежутка Δt к нулю.
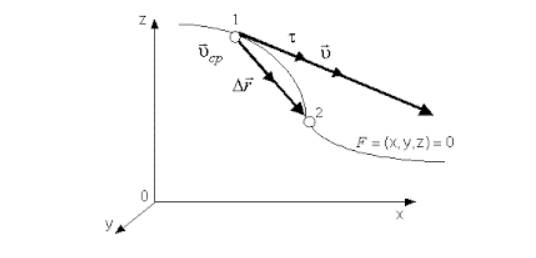
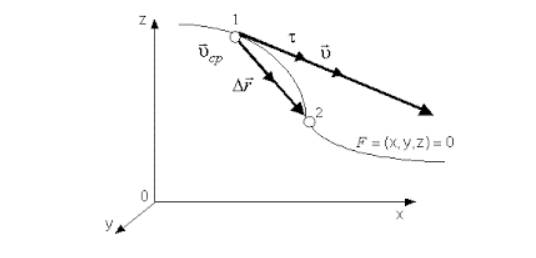
Выясним теперь, как направлен вектор мгновенной скорости. В любой точке траектории вектор мгновенной скорости направлен так, как в пределе, при стремлении промежутка времени Δt к нулю, направлена средняя скорость перемещения. Эта средняя скорость в течение промежутка времени Δt направлена так, как направлен вектор перемещения Δ Из рисунка 1.24 видно, что при уменьшении промежутка времени Δt вектор Δ уменьшая свою длину, одновременно поворачивается. Чем короче становится вектор Δ, тем ближе он к касательной, проведённой к траектории в данной точке М, т. е. секущая переходит в касательную. Следовательно,
мгновенная скорость направлена по касательной к траектории (см. рис. 1.24).
В частности, скорость точки, движущейся по окружности, направлена по касательной к этой окружности. В этом нетрудно убедиться. Если маленькие частички отделяются от вращающегося диска, то они летят по касательной, так как имеют в момент отрыва скорость, равную скорости точек на окружности диска. Вот почему грязь из-под колёс буксующей автомашины летит по касательной к окружности колёс (рис. 1.25).
Понятие мгновенной скорости — одно из основных понятий кинематики. Это понятие относится к точке. Поэтому в дальнейшем, говоря о скорости движения тела, которое нельзя считать точкой, мы можем говорить о скорости какой-нибудь его точки.
Помимо средней скорости перемещения, для описания движения чаще пользуются средней путевой скоростью cps.
Средняя путевая скорость определяется отношением пути к промежутку времени, за который этот путь пройден:
Когда мы говорим, что путь от Москвы до Санкт-Петербурга поезд прошёл со скоростью 80 км/ч, мы имеем в виду именно среднюю путевую скорость движения поезда между этими городами. Модуль средней скорости перемещения при этом будет меньше средней путевой скорости, так как s > |Δ|.
Для неравномерного движения также справедлив закон сложения скоростей. В этом случае складываются мгновенные скорости.
I. Механика
Тестирование онлайн
Виды неравномерного движения
Неравномерным считается движение с изменяющейся скоростью. Скорость может изменяться по направлению. Можно заключить, что любое движение НЕ по прямой траектории является неравномерным. Например, движение тела по окружности, движение тела брошенного вдаль и др.
Иногда встречается неравномерное движение, которое состоит из чередования различного вида движений, например, сначала автобус разгоняется (движение равноускоренное), потом какое-то время движется равномерно, а потом останавливается.
Мгновенная скорость
Охарактеризовать неравномерное движение можно лишь скоростью. Но скорость всегда изменяется! Поэтому можно говорить лишь о скорости в данное мгновение времени. Путешествуя на машине спидометр ежесекундно демонстрирует вам мгновенную скорость движения. Но время при этом надо уменьшить не до секунды, а рассматривать гораздо меньший промежуток времени!
Средняя скорость
У средних величин рисуют сверху горизонтальную черту.
Средняя скорость перемещения. Средняя путевая скорость
Главное запомнить
1) Определение и виды неравномерного движения;
2) Различие средней и мгновенной скоростей;
3) Правило нахождения средней скорости движения
Формула для определения средней скорости*
Часто требуется решить задачу, где весь путь разбит на равные участки, даны средние скорости на каждом участке, требуется найти среднюю скорость движения на всем пути. Неверное решение будет, если сложить средние скорости и разделить на их количество. Ниже выводится формула, которую можно использовать при решении подобных задач. 
Определение мгновенной скорости графически*
Упражнения
Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?
Нельзя, так как в общем случае величина средней скорости не равна среднему арифметическому значению величин мгновенных скоростей. А путь и время не даны.
Какую скорость переменного движения показывает спидометр автомобиля?
Близкую к мгновенной. Близкую, так как промежуток времени должен быть бесконечно мал, а при снятии показаний со спидометра так о времени судить нельзя.
В каком случае мгновенная и средняя скорости равны между собой? Почему?
При равномерном движении. Потому что скорость не изменяется.
Скорость движения молотка при ударе равна 8м/с. Какая это скорость: средняя или мгновенная?
Поезд прошел путь между городами со скоростью 50км/ч. Какая это скорость: средняя или мгновенная?
*Два шарика начали одновременно и с одинаковой скоростью двигаться по поверхностям, имеющим форму, изображенную на рисунке. Как будут отличаться скорости и время движения шариков к моменту их прибытия в точку В? Силу трения не учитывать.
Задача решается графическим способом. Скорости будут одинаковы. Время движения второго шарика меньше. Примерные графики движения шариков приведены на рисунке. Так как пути. пройденные шариками, равны, то, как видно из графика (на графике пути численно равны площадям заштрихованных фигур), время второго шарика меньше времени первого.