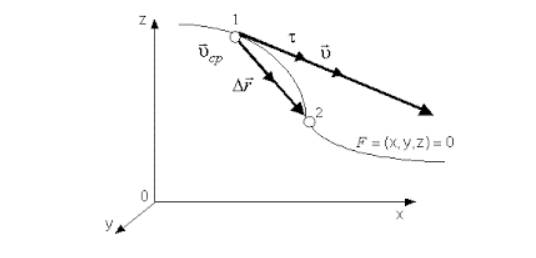
Что называется скоростью материальной точки
Основы механики для чайников. Часть 1: Кинематика
В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.
Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.
Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.
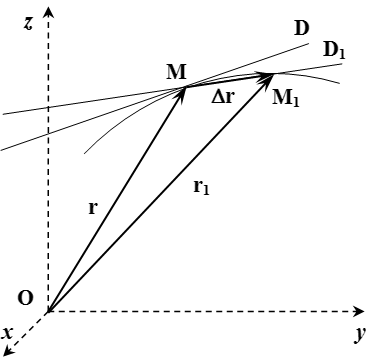
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Перемещение и путь
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.
В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Скорость и ускорение
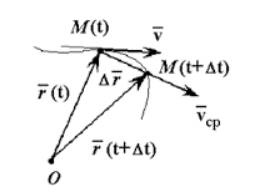
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло
А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
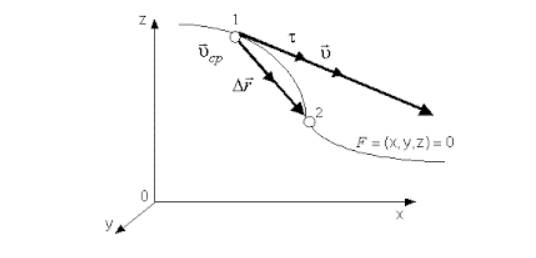
Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.
В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости
Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
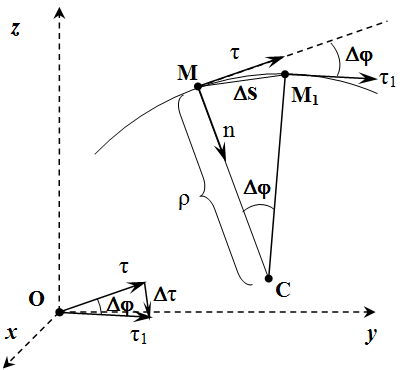
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории
Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.
Здесь R – радиус окружности, по которой движется тело.
Закон равноускоренного движения
Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.
Производная по скорости от времени даст значение ускорения a, которое является константой.
Пример решения задачи
Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.
Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.
Скорость материальной точки
Всего получено оценок: 172.
Всего получено оценок: 172.
Кинематика – это раздел механики, описывающий движение тел без рассмотрения причин этого движения. Одной из характеристик движения является скорость. Рассмотрим ее более подробно.
Материальная точка в Системе Отсчета
При изучении движения необходимо уметь определять положение тела в пространстве. Для этого используются понятие Системы Отсчета и понятие Материальной точки.
Сперва необходимо задаться некоторым базисом – телом, относительно которого будут определяться положение других тел. Такое тело называется Телом Отсчета.
С Телом Отсчета связывается система координат – от одной до трех осей, которые однозначно определяют положение изучаемого тела относительно тела отсчета.
Наконец, поскольку движение всегда происходит во времени, необходима система измерения времени. Некоторый момент принимается за нулевой, кроме того, определяется единица измерения времени.
Тело Отсчета, система координат, связанная с ним и система измерения времени вместе называются Системой Отсчета.
Система координат может задавать положение геометрических точек. А поскольку геометрические размеры и форма тела во многих случаях (но не всегда) не имеют значения, появляется возможность заменить рассматриваемое тело одной точкой. Движение описывается для этой одной точки, а движенbями остальных точек тела пренебрегают. Вся масса тела приписывается этой одной точке. Такая точка называется «материальной».
Скорость движения материальной точки
Движение материальных точек состоит в изменении их положения в Системе Отсчета с течением времени. Изучение этого явления показывает, что оно совершается с разной быстротой. За один и тот же промежуток времени разные материальные точки могут проходить разные расстояния. Поэтому вводится специальная величина для количественной характеристики этой быстроты – скорость.
Чем больше путь, пройденный точкой за некоторое время, тем больше скорость этой точки.
Из формулы скорости материальной точки можно получить единицу скорости. Поскольку единицей расстояния в системе СИ являются метры, а единицей времени – секунды, то единицей скорости являются метры в секунду.
Средняя и мгновенные скорости
Скорость может быть различной не только у разных тел, но и у одного и того же тела в разные моменты времени. Для описания движения, при котором скорость меняется, используются два метода.
$$v_<мгнов>= <ΔS\over <Δt>>, при ΔS \rightarrow 0,Δt\rightarrow 0$$
Мгновенная скорость используется там, где необходимо знать точное значение скорости в конкретном месте пути. Средняя скорость используется там, где важно знать общий результат прохождения рассматриваемого пути.
Что мы узнали?
Скорость материальной точки равна отношению пройденного пути за время его прохождения. Скорость бывает средней и мгновенной. В системе СИ скорость измеряется в метрах в секунду.
Скорость материальной точки – формула
Кинематика – это раздел механики, описывающий движение тел без рассмотрения причин этого движения. Одной из характеристик движения является скорость. Рассмотрим ее более подробно.
Материальная точка в Системе Отсчета
При изучении движения необходимо уметь определять положение тела в пространстве. Для этого используются понятие Системы Отсчета и понятие Материальной точки.
Сперва необходимо задаться некоторым базисом – телом, относительно которого будут определяться положение других тел. Такое тело называется Телом Отсчета.
С Телом Отсчета связывается система координат – от одной до трех осей, которые однозначно определяют положение изучаемого тела относительно тела отсчета.
Наконец, поскольку движение всегда происходит во времени, необходима система измерения времени. Некоторый момент принимается за нулевой, кроме того, определяется единица измерения времени.
Тело Отсчета, система координат, связанная с ним и система измерения времени вместе называются Системой Отсчета.
Рис. 1. Система отсчета в физике.
Система координат может задавать положение геометрических точек. А поскольку геометрические размеры и форма тела во многих случаях (но не всегда) не имеют значения, появляется возможность заменить рассматриваемое тело одной точкой. Движение описывается для этой одной точки, а движенbями остальных точек тела пренебрегают. Вся масса тела приписывается этой одной точке. Такая точка называется «материальной».
Рис. 2. Материальная точка.
Скорость движения материальной точки
Движение материальных точек состоит в изменении их положения в Системе Отсчета с течением времени. Изучение этого явления показывает, что оно совершается с разной быстротой. За один и тот же промежуток времени разные материальные точки могут проходить разные расстояния. Поэтому вводится специальная величина для количественной характеристики этой быстроты – скорость.
Чем больше путь, пройденный точкой за некоторое время, тем больше скорость этой точки.
Из формулы скорости материальной точки можно получить единицу скорости. Поскольку единицей расстояния в системе СИ являются метры, а единицей времени – секунды, то единицей скорости являются метры в секунду.
Средняя и мгновенные скорости
Скорость может быть различной не только у разных тел, но и у одного и того же тела в разные моменты времени. Для описания движения, при котором скорость меняется, используются два метода.
$$v_<мгнов>= <ΔSover <Δt>>, при ΔS rightarrow 0,Δtrightarrow 0$$
Мгновенная скорость используется там, где необходимо знать точное значение скорости в конкретном месте пути. Средняя скорость используется там, где важно знать общий результат прохождения рассматриваемого пути.
Рис. 3. Средняя и мгновенная скорости.
Что мы узнали?
Скорость материальной точки равна отношению пройденного пути за время его прохождения. Скорость бывает средней и мгновенной. В системе СИ скорость измеряется в метрах в секунду.
Кинематика материальной точки
Основные формулы кинематики материальной точки
Приведем основные формулы кинематики материальной точки. После чего дадим их вывод и изложение теории.
Единичный вектор, направленный к центру кривизны траектории точки (вдоль главной нормали):
.
Радиус кривизны траектории:
.
Далее приводится вывод этих формул и изложение теории кинематики материальной точки.
Радиус-вектор и траектория точки
Траектория материальной точки – это линия, вдоль которой происходит движение точки.
Скорость материальной точки
Согласно определению скорости и определению производной:
Производные по времени, в механике, обозначают точкой над символом. Подставим сюда выражение для радиус-вектора:
,
где мы явно обозначили зависимость координат от времени. Получаем:
,
где
,
,
– проекции скорости на оси координат. Они получаются дифференцированием по времени компонент радиус-вектора
.
Таким образом
.
Модуль скорости:
.
Касательная к траектории
Введем направляющий вектор касательной единичной длины:
.
Покажем, что длина этого вектора равна единице. Действительно, поскольку
, то:
.
Абсолютную величину (модуль) вектора скорости мы обозначаем символом с прямыми скобками, или символом без стрелки:
;
Алгебраическая величина скорости:
.
Тогда вектор скорости точки можно представить в следующем виде:
.
Ускорение материальной точки
Аналогично предыдущему, получаем компоненты ускорения (проекции ускорения на оси координат):
;
;
;
.
Модуль ускорения:
.
Тангенциальное (касательное) и нормальное ускорения
Теперь рассмотрим вопрос о направлении вектора ускорения по отношению к траектории. Для этого применим формулу:
.
Дифференцируем ее по времени, применяя правило дифференцирования произведения:
.
Чтобы ответить на этот вопрос, воспользуемся тем, что длина вектора постоянна и равна единице. Тогда квадрат его длины тоже равен единице:
.
Здесь и далее, два вектора в круглых скобках обозначают их скалярное произведение. Продифференцируем последнее уравнение по времени:
;
;
.
Поскольку скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны друг другу. Так как вектор направлен по касательной к траектории, то вектор перпендикулярен к касательной.
Тангенциальное (касательное) ускорение
Радиус кривизны траектории
Нормальное ускорение
Выпишем еще раз следующую формулу:
.
Отсюда видно, что нормальное ускорение вызывает изменение направления скорости точки, и оно связано с радиусом кривизны траектории.
Радиус кривизны траектории:
.
И в заключении заметим, что формулу (4) можно переписать в следующем виде:
.
Здесь мы применили формулу для векторного произведения трех векторов:
,
в которую подставили
.
Итак, мы получили:
;
.
Приравняем модули левой и правой частей:
.
Но векторы и взаимно перпендикулярны. Поэтому
.
Тогда
.
Это известная формула из дифференциальной геометрии для кривизны кривой.
Мгновенная и средняя скорость
Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.
Мгновенная скорость точки. Формулы
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Мгновенной скоростью называют предел, к которому стремится средняя скорость » open=» υ при стремлении промежутка времени ∆ t к 0 :
Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:
Перемещение и мгновенная скорость
Запись модуля вектора υ примет вид:
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ ( t ) d t
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения: