Что называется сетью триангуляции
Триангуляция
Полезное
Смотреть что такое «Триангуляция» в других словарях:
ТРИАНГУЛЯЦИЯ — (позд. лат., от лат. triangalus треугольник.). Тригонометрическое действие, при посредстве которого снимают план с известной местности, разделивши ее на треугольники, которые вычисляются при помощи тригонометрических формул. Словарь иностранных… … Словарь иностранных слов русского языка
Триангуляция — (геодезия) один из методов создания сети опорных геодезических пунктов и сама сеть. В математике Триангуляция (топология) разбиение топологического пространства на симплексы. Триангуляция Делоне … Википедия
Триангуляция — (от лат. triangulum треугольник * a. triangulation, survey by triangulation; н. Triangulation; ф. triangulation; и. tciangulacion) один из методов создания сети опорных геодезич. пунктов, заключающийся в построении рядов или сетей из… … Геологическая энциклопедия
ТРИАНГУЛЯЦИЯ — ТРИАНГУЛЯЦИЯ, см. тригонометрия. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
триангуляция — Метод построения геодезической сети в виде треугольников, в которых измерены их углы и некоторые из сторон [ГОСТ 22268 76] триангуляция Метод определения планового положения геодезических пунктов путём построения на местности системы смежных или… … Справочник технического переводчика
ТРИАНГУЛЯЦИЯ — (от лат. triangulum треугольник) метод определения положения геодезических пунктов построением на местности систем смежно расположенных треугольников, в которых измеряют длину одной стороны (по базису) и углы, а длины других сторон получают… … Большой Энциклопедический словарь
ТРИАНГУЛЯЦИЯ — (тригонометрическая съемка), в навигации и топографической съемке метод определения расстояния. Площадь съемки делится на треугольники. Затем ТЕОДОЛИТОМ измеряют основание треугольника и прилежащие углы. Расстояния от концов основания до… … Научно-технический энциклопедический словарь
ТРИАНГУЛЯЦИЯ — ТРИАНГУЛЯЦИЯ, триангуляции, мн. нет, жен. (от лат. triangulus треугольник). 1. Вычисление углов и протяжений методами тригонометрии (мат.). 2. Определение взаимного расположения точек на поверхности при помощи построения сети треугольников… … Толковый словарь Ушакова
ТРИАНГУЛЯЦИЯ — (Triangulation) наиболее точный прием определения взаимного расположения точек на земной поверхности. При Т. выбираются на открытых и возвышенных местах опорные пункты и закрепляются постройкой специальных знаков. Стороны между знаками образуют… … Морской словарь
ТРИАНГУЛЯЦИЯ — горизонтальная съемка расположения вершин сети треугольников путем измерения длины одной стороны базиса и измерения всех углов. Т. применяется для точной съемки больших участков земной поверхности или для определения длины дуги меридиана или… … Технический железнодорожный словарь
триангуляция — сущ., кол во синонимов: 2 • аэротриангуляция (1) • стереотриангуляция (1) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Триангуляция (в геодезии)
Т. имеет большое научное и практическое значение. Она служит для: определения фигуры и размеров Земли методом градусных измерений; изучения горизонтальных движений земной коры; обоснования топографических съёмок в различных масштабах и целях; обоснования различных геодезических работ при изыскании, проектировании и строительстве крупных инженерных сооружений, при планировке и строительстве городов и т.д.
При построении Т. исходят из принципа перехода от общего к частному, от крупных треугольников к более мелким. В связи с этим Т. подразделяется на классы, отличающиеся точностью измерений и последовательностью их построения. В малых по территории странах Т. высшего класса строят в виде сплошных сетей треугольников. В государствах с большой территорией (СССР, Канада, КНР, США и др.) Т. строят по некоторой схеме и программе. Наиболее стройная схема и программа построения Т. применяется в СССР.
Вершины треугольников Т. обозначаются на местности деревянными или металлическими вышками высотой от 6 до 55 м в зависимости от условий местности (см. Сигнал геодезический ). Пункты Т. в целях долговременной их сохранности на местности закрепляются закладкой в грунт особых устройств в виде металлических труб или бетонных монолитов с вделанными в них металлическими марками (см. Центр геодезический ), фиксирующими положение точек, для которых даются координаты в соответствующих каталогах.
Лит.: Красовский Ф. Н., Данилов В. В., Руководство по высшей геодезии, 2 изд., ч. 1, в. 1‒2, М., 1938‒39; Инструкция о построении государственной геодезической сети СССР, 2 изд., М., 1966.
Землянка
суббота, 7 июля 2012 г.
Триангуляция и геодезические пункты
Триангуляция (в геодезии)
Значение слова «Триангуляция (в геодезии)» в Большой Советской Энциклопедии
Триангуляция (от лат. triangulum — треугольник), один из методов создания сети опорных геодезических пунктов и сама сеть, созданная этим методом; состоит в построении рядов или сетей примыкающих друг к другу треугольников и в определении положения их вершин в избранной системе координат. В каждом треугольнике измеряют все три угла, а одну из его сторон определяют из вычислений путём последовательного решения предыдущих треугольников, начиная от того из них, в котором одна из его сторон получена из измерений. Если сторона треугольника получена из непосредственных измерений, то она называется базисной стороной Триангуляция (в геодезии) В прошлом вместо базисной стороны непосредственно измеряли короткую линию, называемую базисом, и от неё путём тригонометрических вычислений через особую сеть треугольников переходили к стороне треугольника Триангуляция (в геодезии) Эту сторону Триангуляция (в геодезии) обычно называют выходной стороной, а сеть треугольников, через которые она вычислена,— базисной сетью. В рядах или сетях Триангуляция (в геодезии) для контроля и повышения их точности измеряют большее число базисов или базисных сторон, чем это минимально необходимо.
Принято считать, что метод Триангуляция (в геодезии) изобрёл и впервые применил В. Снеллиус в 1615—17 при прокладке ряда треугольников в Нидерландах для градусных измерений. Работы по применению метода Триангуляция (в геодезии) для топографических съёмок в дореволюционной России начались на рубеже 18—19 вв. К началу 20 в. метод Триангуляция (в геодезии) получил повсеместное распространение.
Триангуляция (в геодезии) имеет большое научное и практическое значение. Она служит для: определения фигуры и размеров Земли методом градусных измерений; изучения горизонтальных движений земной коры; обоснования топографических съёмок в различных масштабах и целях; обоснования различных геодезических работ при изыскании, проектировании и строительстве крупных инженерных сооружений, при планировке и строительстве городов и т.д.
При построении Триангуляция (в геодезии) исходят из принципа перехода от общего к частному, от крупных треугольников к более мелким. В связи с этим Триангуляция (в геодезии) подразделяется на классы, отличающиеся точностью измерений и последовательностью их построения. В малых по территории странах Триангуляция (в геодезии) высшего класса строят в виде сплошных сетей треугольников. В государствах с большой территорией (СССР, Канада, КНР, США и др.) Триангуляция (в геодезии) строят по некоторой схеме и программе. Наиболее стройная схема и программа построения Триангуляция (в геодезии) применяется в СССР.
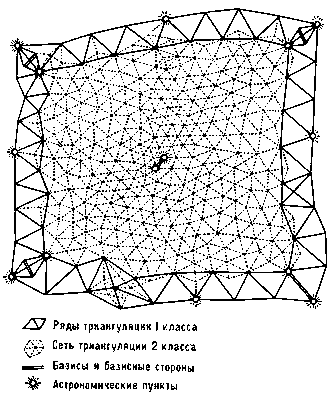
Государственная Триангуляция (в геодезии) в СССР делится на 4 класса (рис.). Государственная Триангуляция (в геодезии) СССР 1-го класса строится в виде рядов треугольников со сторонами 20—25 км, расположенных примерно вдоль меридианов и параллелей и образующих полигоны с периметром 800—1000 км. Углы треугольников в этих рядах измеряют высокоточными теодолитами, с погрешностью не более ± 0,7«. В местах пересечения рядов Триангуляция (в геодезии) 1-го класса измеряют базисы при помощи мерных проволок (см. Базисный прибор), причём погрешность измерения базиса не превышает 1 : 1000000 доли его длины, а выходные стороны базисных сетей определяются с погрешностью около 1 : 300 000. После изобретения высокоточных электрооптических дальномеров стали измерять непосредственно базисные стороны с погрешностью не более 1 : 400 000. Пространства внутри полигонов Триангуляция (в геодезии) 1-го класса покрывают сплошными сетями треугольников 2-го класса со сторонами около 10—20 км, причём углы в них измеряют с той же точностью, как и в Триангуляция (в геодезии) 1-го класса. В сплошной сети Триангуляция (в геодезии) 2-го класса внутри полигона 1-го класса измеряется также базисная сторона с указанной выше точностью. На концах каждой базисной стороны в Триангуляция (в геодезии) 1-го и 2-го классов выполняют астрономические определения широты и долготы с погрешностью не более ± 0,4«, а также азимута с погрешностью около ± 0,5«. Кроме того, астрономические определения широты и долготы выполняют и на промежуточных пунктах рядов Триангуляция (в геодезии) 1-го класса через каждые примерно 100 км, а по некоторым особо выделенным рядам и значительно чаще.
В практике СССР допускается вместо Триангуляция (в геодезии) применять метод полигонометрии. При этом ставится условие, чтобы при построении опорной геодезической сети тем и др. методом достигалась одинаковая точность определения положения пунктов земной поверхности.
Вершины треугольников Триангуляция (в геодезии) обозначаются на местности деревянными или металлическими вышками высотой от 6 до 55 м в зависимости от условий местности (см. Сигнал геодезический). Пункты Триангуляция (в геодезии) в целях долговременной их сохранности на местности закрепляются закладкой в грунт особых устройств в виде металлических труб или бетонных монолитов с вделанными в них металлическими марками (см. Центр геодезический), фиксирующими положение точек, для которых даются координаты в соответствующих каталогах.
Координаты пунктов Триангуляция (в геодезии) определяют из математической обработки рядов или сетей Триангуляция (в геодезии) При этом реальную Землю заменяют некоторым референц-эллипсоидом, на поверхность которого приводят результаты измерения углов и базисных сторон Триангуляция (в геодезии) В СССР принят референц-эллипсоид Красовского (см. Красовского эллипсоид). Построение Триангуляция (в геодезии) и её математическая обработка приводят к созданию на всей территории страны единой системы координат, позволяющей ставить топографо-геодезические работы в разных частях страны одновременно и независимо друг от друга. При этом обеспечивается соединение этих работ в одно целое и создание единой общегосударственной топографической карты страны в установленном масштабе.
Лит.: Красовский Ф. Н., Данилов В. В., Руководство по высшей геодезии, 2 изд., ч. 1, в. 1—2, М., 1938—39; Инструкция о построении государственной геодезической сети СССР, 2 изд., М., 1966.
Триангуляция и определении расстояний
Потребность в измерении громадных, в сотни километров, расстояний – как на суше, так и на море – появилась ещё в древние времена. Метод триангуляции позволил высчитать огромные расстояния и определить фигуру Земли.
Понятие триангуляции
Пежде чем говорить о методе триангуляции, рассмотрим суть термина. Триангуляция — это сеть прилегающих друг к другу треугольников разного вида, можно сравнить с примыканием паркетин; наряду с этим существенно, что примыкают только целые стороны, так что вершина одного треугольника не может лежать внутри стороны другого. Триангуляции сыграли наиболее значимую роль в измерении расстояний на земной поверхности, и тем самым — и в определении фигуры Земли.
История измерения земных расстояний
Капитаны судов, как мы знаем из детских книг, меряют расстояния числом выкуренных трубок. Близок к этому метод, использовавшийся во II в. до н. э. известным древнегреческим философом, великим математиком и астрономом Посидонием, учителем Цицерона: морские расстояния Посидоний измерял длительностью плавания (с учётом, очевидно, скорости судна).
Но ещё раньше, в III веке до н. э., другой известный древний грек, управлявший библиотекой в Александрии великий математик и астроном Эратосфен, мерил сухопутные расстояния по времени и скорости движения торговых караванов. Возможно предположить, что именно так Эратосфен замерил расстояние между Сиеной и Александрией, которая в настоящее время называется Асуаном (если наблюдать по современной карте, получается приблизительно 850 км). Это расстояние было для него очень серьёзным. Эратосфен желал измерить длину меридиана и думал, что эти два египетских города лежат на одном и том же меридиане; не смотря на то, что это в конечном итоге не совсем так, но близко к истине. Найденное расстояние он принял за протяжённость дуги меридиана. Объединив эту длину с наблюдением полуденных высот Солнца над горизонтом в Сиене и Александрии, он потом путём красивых геометрических рассуждений вычислил протяжённость всего меридиана и, как следствие, радиус земного шара. Ещё в XVI веке расстояние (приблизительно 100 км) между Амьеном и Парижем определили подсчитав обороты колеса экипажа. Неточность результатов аналогичных измерений очевидна и объяснима. Но уже в следующем веке голландский математик, астроном и оптик Снеллиус смог изобрести принципиально новый, излагаемый ниже метод триангуляции и с его помощью в 1615–1617 гг. измерил дугу меридиана, имеющую угловой размер 1° 11′ 30″.
Суть метода триангуляции при измерении расстояний
Посмотрим, как триангуляция позволяет определять расстояния. Вначале выбирают какой-нибудь фрагмент или участок земной плоскости, включающий в себя оба пункта, расстояние между которыми стремятся найти, и доступный для проведения измерительных работ на местности. Данный участок покрывают сетью множества треугольников, образующих триангуляцию т. е. триангулируют. После этого выбирают один из треугольников триангуляции; будем называть его начальным. Потом выбирают одну из сторон начального треугольника. Она является базой, и её длину тщательно измеряют. В вершинах начального треугольника строят башни (или вышки) — с таким расчётом, чтобы каждая была видна с других башен. Поднявшись на башню, расположенную в одной из вершин базы, измеряют угол, под которым видны две другие башни. Затем поднимаются на башню, расположенную в другой вершине базы, и делают то же самое. Так, путем непосредственного измерения, получают сведения о длине одной из сторон начального треугольника (в частности: о длине базы) и о величине прилегающих к ней углов. По известным и простым формулам тригонометрии (с применением косинуса, синуса, тангенса и катангенса) вычисляют длины 2-х других сторон этого треугольника. Каждую из них можно принять за новую базу, причём измерять её длину уже не нужно. Используя ту же процедуру, возможно теперь определить длины сторон и углы любого из треугольников, примыкающих к начальному, и т. д. Важно осмыслить, что непосредственное измерение какого-либо расстояния выполняют лишь 1 раз, а дальше уже измеряют только углы между направлениями на башни, что несравненно легче и может быть сделано с высокой точностью. По завершении процесса оказываются установленными величины всех участвующих в триангуляции отрезков и углов. А это, в свою очередь, позволяет находить любые расстояния в пределах участка поверхности, покрытого триангуляцией.
Длина дуги меридиана от широты Северного Ледовитого океана до широты Чёрного моря
В частности, как раз так в XIX веке нашлась длина дуги меридиана от широты Северного Ледовитого океана (в районе Хaммерфеста на острове Квaлё – Норвегия) до широты Чёрного моря (в районе низовья Дуная). Она была сформирована из длин 12 отдельных дуг. Процедура упрощалась тем, что для нахождения длины дуги меридиана вовсе не нужно, чтобы составляющие дуги примыкали друг к другу концами; достаточно, чтобы концы соседних дуг находились на одной и той же широте. (К примеру, если необходимо определить расстояние между семидесятой и сороковой параллелями, то возможно на одном меридиане замерить расстояние между 70-й и 50-й параллелями, на другом меридиане — расстояние между 50-й и 40-й параллелями, а после этого сложить полученные расстояния.) Общее число треугольников триангуляции составило 258, длина дуги равнялась 2800 км. Чтобы исключить ошибки и неточности, неизбежные при измерениях, а при вычислениях вероятные, 10 подверглись прямому измерению на местности. Измерения были проведены в перид с 1816 по 1855 г.г., а итоги были изложены в двух томах «Дуга меридиана в 25° 20′ между Дунаем и Ледовитым морем» (СПб., 1856–1861), написанным замечательным русским геодезистом и астрономом Василием Яковлевичем Струве (1793–1864), осуществившего российскую часть измерений.
Тема: Геодезические сети. Топографические съемки
_______ Для составления карт и планов, решения геодезических задач в том числе геодезического обеспечения строительства, на поверхности Земли располагают ряд точек, связанных между собой единой системой координат. Эти точки маркируют на поверхности Земли или в зданиях и сооружениях центрами (знаками).
_______ Геодезическая сеть – это система закрепленных точек земной поверхности, положение которых определено в общей для них системе геодезических координат.
_______ Геодезические сети подразделяют на плановые и высотные : первые служат для определения координат X и Y геодезических центров, вторые — для определения их высот.
_______ Принцип построения плановых геодезических сетей заключается в следующем. На местности выбирают точки, взаимное положение которых представляется в виде геометрических фигур: треугольников, четырехугольников, ломаных линий и т.д. Причем точки выбирают с таким расчетом, чтобы некоторые элементы фигур (стороны, углы) можно было бы непосредственно измерить, а все другие элементы вычислить по данным измерений. Например, в треугольнике достаточно измерить одну сторону и три угла (один для контроля правильности измерений) или две стороны и два угла (один для контроля правильности измерений), а остальные стороны и углы вычислить. Для вычисления плановых координат вершин выбранных точек необходимо кроме элементов геометрических фигур знать еще дирекционный угол стороны одной из фигур и координаты одной из вершин.
_______ Сети строят по принципу перехода от общего к частному, т. е. от сетей с большими расстояниями между пунктами и высокоточными измерениями к сетям с меньшими расстояниями и менее точным.
_______ Геодезические сети подразделяют на четыре вида: государственные, сгущения, съемочные и специальные. Государственные геодезические сети служат исходными для построения всех других видов сетей. Началом единого отсчета плановых координат в Российской Федерации служит центр круглого зала Пулковской обсерватории в Санкт-Петербурге.
2. Методы создания геодезических сетей
_______ Плановые геодезические сети создаются методами триангуляции, полигонометрии и трилатерации. При построении геодезической сети методом триангуляции на местности закрепляется ряд точек, которые в своей совокупности образуют систему треугольников. В треугольниках измеряются все углы и некоторые стороны, которые называются базисными. По длине базисной стороны и измеренным углам, вычисляют длины всех сторон, а затем координаты всех пунктов сети.
 |
_______ Метод полигонометрии заключается в построении на местности системы ломанных линий, называемых полигонометрическими ходами. Эти ходы прокладывают обычно между пунктами триангуляции. В полигонометрических ходах измеряются все углы поворота и длины всех сторон.
 |
_______ При построении сети методом трилатерации на местности также строится сеть треугольников, в которых при помощи высокоточных дальномеров измеряются все стороны.
 |
_______ Сети сгущения строят для дальнейшего увеличения плотности (числа пунктов, приходящихся на единицу площади) государственных сетей. Плановые сети сгущения подразделяют на 1-й.и 2-й разряды.
_______ Съемочные сети — это тоже сети сгущения, но с еще большей плотностью. С точек съемочных сетей производят непосредственно съемку предметов местности и рельефа для составления карт и планов различных масштабов.
_______ Специальные геодезические сети создают для геодезического обеспечения строительства сооружений. Плотность пунктов, схема построения и точность этих сетей зависят от специфических особенностей строительства.
_______ Государственные высотные геодезические сети создают для распространения по всей территории страны единой системы высот. За начало высот в Российской Федерации и некоторых других странах принят средний уровень Балтийского моря, определение которого проводилось в период с 1825 до 1840 г. Этот уровень отмечен горизонтальной чертой на медной металлической пластине, укрепленной в устое моста через обводной канал в Кронштадте.
_______ Между пунктами государственных высотных геодезических сетей высокой точности (1-го класса) размещают пункты высотных сетей низших классов (2-го, 3-го и т.д.). Несколько пересекающихся ходов называют сетями. Как правило, сети создают из ходов, прокладываемых между тремя или более точек. В целом точки (реперы) высотных сетей, называемых нивелирными, достаточно равномерно распределены на территории страны.
_______ На незастроенной территории расстояния между реперами составляют 5. 7 км, в го- родах сеть реперов в 10 раз плотнее
_______ Для решения ограниченного круга вопросов при изысканиях, строительстве и эксплуатации зданий и сооружений создают высотную сеть технического класса.
_______ Как правило, сети образуют полигоны с узловыми точками (общими точками пересечения двух или более ходов одного и того же класса). Каждый нивелирный ход опирается обоими концами на реперы ходов более высокого класса или узловые точки.
3. Закрепление на местности пунктов геодезических сетей
_______ Точки геодезических сетей закрепляют на местности знаками. По местоположению знаки бывают: грунтовые и стенные, заложенные в стены зданий и сооружений; металлические, железобетонные, деревянные, в виде откраски и т.д.; по назначению — постоянные, к которым относятся все знаки государственных геодезических сетей, и временные, устанавливаемые на период изысканий, строительства, реконструкции, наблюдений и т.д.
 |
_______ Для того чтобы с одного знака был виден другой (смежный),над подземными центрами устанавливают наружные знаки в виде металлических или деревянных трех- или четырехгранных пирамид или сигналов.
 |
_______ Как правило, пункты плановых разбивочных сетей и сетей сгущения закрепляют подземными центрами, такими же как и пункты государственных сетей. Так как расстояния между этими пунктами сравнительно небольшие, оформления их наружными знаками не требуется. Знаки могут закладывать в зданиях и сооружениях, в этом случае их называют стенными.
_______ Иногда для различных целей могут создаваться местные геодезические сети. Обязательным требованием при установлении местных систем координат является обеспечение возможности перехода от местной системы координат к государственной системе координат, который осуществляется с использованием параметров перехода (ключей).
_______ Каждая местная система координат может создаваться с одной или несколькими трех или шести градусными зонами. Параметры местных систем координат и ключи перехода к государственной системе координат (формулы и правила, по которым координаты точек в одной системе можно получить в другой системы) устанавливает Росреестр по согласованию с Минобороны РФ.
4. Топографические съемки, ее виды
_______ Существуют следующие виды топографических съемок:
_______ • теодолитная (горизонтальная),
_______ • мензульная и др.
4.1 Что такое теодолитная съемка
_______ Теодолитной съемкой называется горизонтальная или контурная съемка местности, которая выполняется с помощью теодолита.
_______ Для проектирования зданий, сооружений необходимо на район строительства иметь топографические материалы – планы, карты. При отсутствии таких материалов выполняют съемку данного участка местности.
4.2 Сущность теодолитной съемки
_______ Теодолитная съемка выполняется с помощью теодолита и рулетки (или дальномера соотвествующей точности). В результате теодолитной съемки получают контурный план местности.
_______ Съемку контуров выполняют на основе съемочных теодолитных ходов, которые прокладываются в виде :
а) замкнутых ходов,
б) разомкнутых ходов,
в) диагональных ходов.
 |
 |
_______ Теодолитная съемка складывается из следующих видов работ :
• прокладка теодолитных ходов и привязка их к пунктам геодезической сети,
• съемка ситуации,
• обработка результатов полевых измерений,
• построение плана.
5. Прокладка теодолитных ходов. Привязка к пунктам геодезической сети
_______ Привязка теодолитных ходов заключается в измерении привычных углов между сторонами теодолитного хода и геодезической сети, обязательно с контролем.
 |
6. Съемка ситуации
_______ Съемка ситуации заключается в привязке контуров и предметов местности к сторонам и вершинам теодолитного хода.
6.1. Способ прямоугольных координат (способ перпендикуляров)
 |
6.2. Способ полярных координат (полярный способ)
 |
6.3. Способ линейных засечек
_______ Треугольники стараются делать близкими к равносторонним. Линейная засечка применяется часто при съемке строений. В этом случае расстояния измеряются лентой или рулеткой.
 |
6.4. Способ угловых засечек
_______ Способ угловых засечек применяется в тех случаях, когда определить положение точки при помощи линейных измерений не удается.
 |
6.5. Способ створов
 |
_______ Абрис – это схематический чертеж, составленный в произвольном масштабе.
_______ На абрисе зарисовывается снимаемая ситуация и записываются результаты выполняемых при съемке угловых и линейных измерений. Абрис составляется отдельно на каждую сторону теодолитного хода. На основе абриса производится нанесение контуров местности на план.