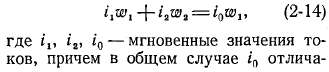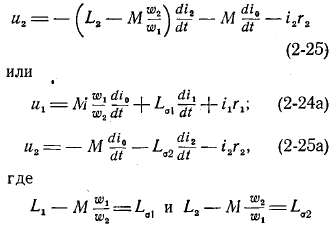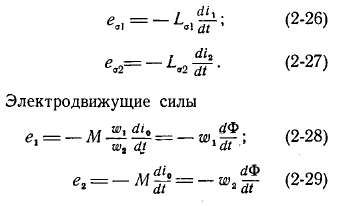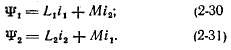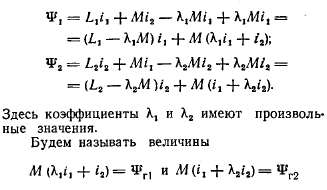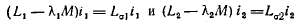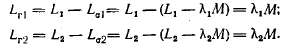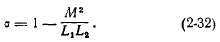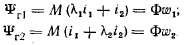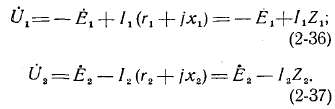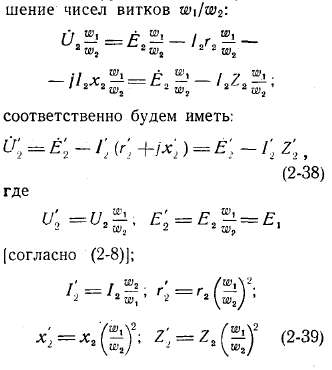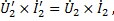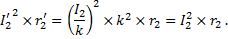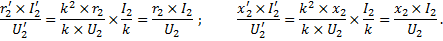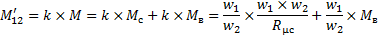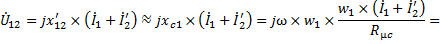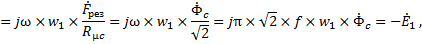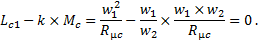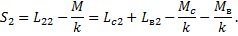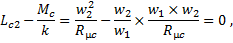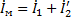Что называется приведенными величинами вторичной обмотки

Что называется приведенными величинами вторичной обмотки

2-4. Работа при нагрузке

а) Первичный ток. Работа трансформатора при нагрузке характеризуется наличием тока I₂ во вторичной обмотке, увеличение которого (как будет ясно из последующего) вызывает увеличение тока I₁ в первичной обмотке.

При нагрузке трансформатора магнитный поток Ф в его сердечнике, называемый главным потоком, создается согласно закону полного тока совместным действием н. с. обеих обмоток:

ется от мгновенного значения тока холостого хода.

Так как мы принимаем токи синусоидальными, то можем написать (рис. 2-1):

б) Уравнения напряжений. Будем вначале считать, что потокосцеп-ления обмоток трансформатора пропорциональны их токам и что магнитные потери в сердечнике отсутствуют (такие условия получаются в воздушном трансформаторе). При этом, так же как для двух магнитно связанных контуров, можем написать следующие уравнения напряжений первичной и вторичной обмоток трансформатора:

— индуктивности рассеяния первичной и вторичной обмоток; им соответствуют э. д. с. рассеяния:

рассматриваются как э. д. с, наведенные главным потоком Ф.

Приведем здесь уравнения, относящиеся к общей теории двух магнитно связанных обмоток. Для потокосцеплений этих обмоток можем написать:

Вычтем и прибавим с правой стороны написанных равенств одни и те же величины:

главными потокосцеплениями обмоток, а величины

их потокосцеплениями рассеяния. Главными индуктивностями обмоток назовем величины

Общий коэффициент рассеяния равен:

Коэффициенты рассеяния обмоток равны отношениям индуктивностей рассеяния к главным индуктивностям:

Подразделяя произведение λ₁λ₂=1 любым образом на λ₁ и λ₂, можно потокосцепления рассеяния приписать одной или другой обмотке или обеим обмоткам. Мы не имеем также достаточно данных, чтобы однозначно определить главный поток, о котором говорилось ранее. Однако внести определенность в понятия индуктивностей рассеяния мы можем только в том случае, если допустим, что в трансформаторе существует главный поток Ф, созданный н. с. обеих обмоток и сцепляющийся со всеми их витками. Такое допущение, очевидно, в большой степени оправдывается в применении к нормальным трансформаторам со стальным сердечником.

Мы можем теперь написать:

Теория электрических машин также основана, как мы покажем в дальнейшем, на допущении существования главного потока, не зависящего от полей рассеяния.

Считая, что токи и э. д. с. уравнений (2-26)—(2-29) изменяются во вре-

мени по закону синуса, мы можем эти уравнения переписать в комплексной форме:

Ранее при рассмотрении режима холостого хода мы пренебрегали полем вне сердечника трансформатора. В действительности это поле согласно закону полного тока должно существовать. Оно называется полем рассеяния. Созданные им потокосцепления обмоток малы по сравнению с потокосцеплениями обмоток, созданными главным потоком, С большим приближением к действительным условиям можно считать, что поле рассеяния и поле в сердечнике, соответствующее главному потоку, существуют независимо одно от другого.

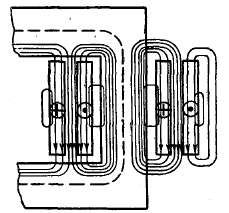
На рис. 2-13 представлена приближенная картина поля рассеяния, которую кладут в основу расчета потоко-сцеплений рассеяния. Здесь пунктирной линией показан путь главного потока Ф, сплошными линиями показаны индукционные линии поля рассея-

Рис. 2-13. Приближенная картина поля рассеяния трансформатора с концентрическими обмотками. Крестиками и точками условно показаны направления токов в обмотках для рассматриваемого момента времени.

ния. Они могут быть условно разделены на две группы: сцепляющиеся с первичной обмоткой и сцепляющиеся со вторичной обмоткой. Магнитные сопротивления для потоков соответствующих индукционных трубок рассеяния определяются в основном сопротивлениями тех их частей, которые проходят вдоль обмоток и в промежутке между ними. Их можно принять постоянными, поскольку потоки трубок проходят по материалам (медь, изоляция, воздух или масло), для которых μ = const. Магнитными сопротивлениями потоков трубок вне обмоток и промежутка между ними можно пренебречь, так как здесь они проходят в основном по стали сердечника.

С учетом приведенных равенств (2-35) уравнения напряжений (2-24а) и (2-25а) для установившегося режима могут быть написаны в комплексной форме:

Уравнения (2-36) и (2-37) называются векторными уравнениями напряжений трансформатора (здесь имеются в виду временные векторы напряжений, э. д. с. и токов).

В реальном трансформаторе со стальным сердечником при его работе возникают магнитные потери. Для их учета мы должны считать, так же как при холостом ходе, что ток I₀ имеет наряду с реактивной составляющей I_0р активную составляющую I_0а [см. уравнения (2-9)—(2-13)]; однако обе эти составляющие мы должны отнести не

Вследствие нелинейной связи между потоком Ф и результирующим током i₀ кривая последнего при синусоидальном потоке Ф будет несинусоидальной (§ 2-13). Для облегчения анализа зависимостей, характеризующих работу трансформатора, ток i₀ принимается синусоидальным с действующим значением, равным тому же значению действительного тока. Такое допущение не может привести к заметной ошибке из-за относительной малости тока I₀.

в) Приведение величин вторичной обмотки к числу витков первичной обмотки. Указанное приведение получим, если помножим уравнение (2-37) на отно-

представляют собой величины вторичной обмотки, приведенные к числу витков первичной обмотки. Такое приведение величин вторичной обмотки облегчает исследование работы трансформатора: делает более удобным построение для него векторных диаграмм (§ 2-4,г), позволяет построить удобную для расчетов схему соединения его активных и индуктивных сопротивлений, называемую схемой замещения трансформатора, где магнитная связь между обмотками заменена электрической связью между ними (§ 2-5).

Можно считать, что приведение величин вторичной обмотки к числу витков первичной обмотки сводится

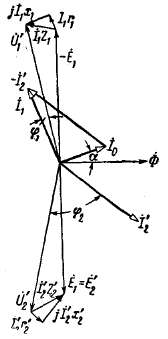
Рис. 2-14. Векторная диаграмма трансформатора, работающего с отстающим током.

же найти соотношения между приведенными и действительными величинами вторичной обмотки. Они получаются такими же, как и (2-39).

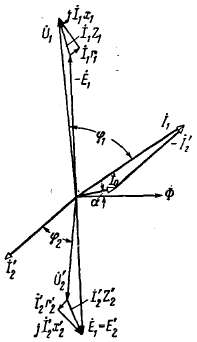
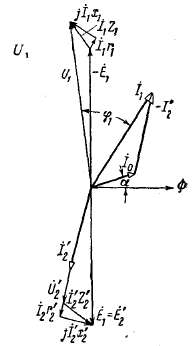
г) Векторные диаграммы. Векторные диаграммы наглядно показывают соотношения между токами, э. д. с. и напряжениями обмоток. Они строятся в соответствии с уравнениями (2-19), (2-36) и (2-38).

На рис. 2-14 — 2-16 представлены диаграммы трансформатора, работающего с различными нагрузками.

Векторная диаграмма трансформатора, работающего, например, с отстающим током (рис. 2-14), при заданных

Рис. 2-15. Векторная диаграмма трансформатора, работающего с cos φ₂=l.

Рис. 2-16. Векторная диаграмма трансформатора, работающего с опережающим током.

Приведенные ранее уравнения напряжений и токов, а также векторные диаграммы относятся к однофазному трансформатору или к одной фазе трехфазного трансформатора. Различие токов холостого хода отдельных фаз трехфазного трансформатора вследствие несимметрии их магнитных

цепей не имеет практического значения, так как токи холостого хода составляют обычно небольшую долю номинального тока; параметры же отдельных фаз r₁, r’₂, x₁, x’₂ можно считать одинаковыми.

Источник

Приведение величин вторичной обмотки к числу витков первичной обмотки

Указанное приведение получим, если помножим уравнение (2-37) на отношение чисел витков

соответственно будем иметь

представляют собой величины вторичной обмотки, приведенные к числу витков первичной обмотки. Такое приведение величин вторичной обмотки облегчает исследование работы трансформатора: делает более удобным построение для него векторных диаграмм (§ 2-4,г), позволяет построить удобную для расчетов схему соединения его активных и индуктивных сопротивлений, называемую схемой замещения трансформатора, где магнитная связь между обмотками заменена электрической связью между ними (§ 2-5).

г) Векторные диаграммы.

Векторные диаграммы наглядно показывают соотношения между токами, э.д.с. и напряжениями обмоток. Они строятся в соответствии с уравнениями (2-19), (2-36) и (2-38).

На рис. 2-14 — 2-16 представлены диаграммы трансформатора, работающего с различными нагрузками.

Рис. 2-14. Векторная диаграмма трансформатора работающего с отстающим током.

Рис. 2-15. Векторная диаграмма трансформатора, работающего с 1.

Рис. 2-16. Векторная диаграмма трансформатора, работающего с опережающим током.

Векторная диаграмма трансформатора, работающего, например, с отстающим током (рис. 2-14), при заданных может быть построена следующим образом.

Обратная задача, с которой обычно приходится иметь дело на практике, когда заданы и cos φ₂ и требуется найти решается в большинстве случаев аналитически, как показано в § 2-8.

Диаграммы на рис. 2-14 и 2-15 показывают, что напряжение при нагрузке меньше, чем напряжение при холостом ходе, и тем меньше, чем больше сопротивления обмоток r₁, x₁, r₂, и угол φ₂.

Значение тока зависит от значения э.д.с. ; следовательно, оно изменяется с изменением тока нагрузки, если = const. Однако это изменение невелико, и при практических расчетах можно принять Ф_м=const и =const.

Диаграмма на рис. 2-16 показывает, что при работе трансформатора с опережающим током напряжение на его зажимах может быть выше, чем при холостом ходе, так как в этом случае э.д.с. возрастает и, кроме того, результирующая э.д.с. + больше, чем ( ― э.д.с. рассеяния вторичной обмотки, приведенная к числу витков первичной обмотки).

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Приведение параметров вторичной обмотки и схема замещения приведенного трансформатора

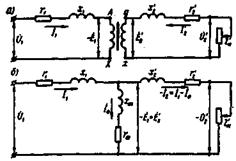
В общем случае параметры первичной обмотки трансформатора отличаются от параметров вторичной обмотки. Эта разница наиболее ощутима при больших коэффициентах трансформации, что затрудняет расчеты и построение векторных диаграмм, так как в этом случае векторы электрических величин первичной обмотки значительно отличаются по своей длине от одноименных векторов вторичной обмотки. Указанные затруднения устраняются приведением всех параметров трансформатора к одинаковому числу витков, обычно к числу витков первичной обмотки w₁. С этой целью все величины, характеризующие вторичную цепь трансформатора, — ЭДС, напряжение, ток и сопротивления — пересчитывают на число витков w₁ первичной обмотки.

Таким образом, вместо реального трансформатора с коэффициентом трансформации k = w₁/w₂ получают эквивалентный трансформатор с k=w₁/w’₂=1, где w’₂=w₁. Такой трансформатор называют приведенным. Однако приведение вторичных параметров трансформатора не должно отразиться на его энергетических показателях: все мощности и фазовые сдвиги во вторичной обмотке приведенного трансформатора должны остаться такими, как и в реальном трансформаторе.

Так, электромагнитная мощность вторичной обмотки реального трансформатора Е₂I₂ должна быть равна электромагнитной мощности вторичной обмотки приведенного трансформатора:

(1.27)

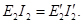
Подставив значение приведенного тока вторичной обмотки I₂= I₂(w₂/w₁,) в (1.27), получим формулу приведенной вторичной ЭДС:

(1.28)

(1.29)

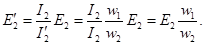
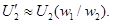
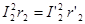
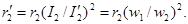
Из условия равенства потерь в активном сопротивлении вторичной обмотки имеем . Определим приведенное активное сопротивление:

(1.30)

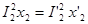
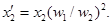
Приведенное индуктивное сопротивление рассеяния вторичной обмотки определяют из условия равенства реактивных мощностей ,откуда

(1.31)

Приведенное полное сопротивление вторичной обмотки трансформатора

(1.32)

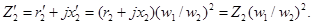
Приведенное полное сопротивление нагрузки, подключенной на выводы вторичной обмотки, определим по аналогии с (1.32):

(1.33)

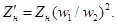
Уравнения напряжений и токов для приведенного трансформатора имеют вид

(1.34)

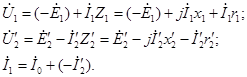
Эти уравнения устанавливают аналитическую связь между параметрами трансформатора во всем диапазоне нагрузок от режима х.х. до номинальной.

Еще одним средством, облегчающим исследование электромагнитных процессов и расчет трансформаторов, является применение электрической схемы замещения приведенного трансформатора. На рис. 1.18, а представлена эквивалентная схема приведенного трансформатора, на которой сопротивления r и х условно вынесены из соответствующих обмоток и включены последовательно им. Как было установлено ранее, в приведенном трансформаторе k = 1, а поэтому 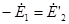. В результате точки А и а, атакже точки X и х на схеме имеют одинаковые потенциалы, что позволяет электрически соединить указанные точки, получив Т–образную схему замещения приведенного трансформатора (рис. 1.18, б). В электрической схеме замещения трансформатора магнитная связь между цепями заменена электрической.

Рис. 1.18. Эквивалентная схема (в) и схема замещения (б) приведенного

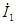
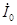
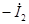
Схема замещения приведенного трансформатора удовлетворяет всем уравнениям ЭДС и токов приведенного трансформатора (1.34) и представляет собой совокупность трех ветвей: первичной — сопротивлением Z₁ = r₁ + jx₁ и током ; намагничивающей — сопротивлением Z_m=r_m+jx_m и током ; вторичной — с двумя сопротивлениями: сопротивлением собственно вторичной ветви Z’₂ = r’₂ + jx’₂ и сопротивлением нагрузки Z’_H = r_н‘ ± jx’_H и током . Изменением сопротивления нагрузки Z’_H на схеме замещения могут быть воспроизведены все режимы работы трансформатора.

Параметры ветви намагничивания Z_m = r_m + jx_m определяются током х.х. Наличие в этой ветви активной составляющей r_m обусловлено магнитными потерями в трансформаторе (см. § 1.14).

Все параметры схемы замещения, за исключением Z’_H, являются постоянными для данного трансформатора и могут быть определены из опыта х.х. и опыта к.з. (см. §1.11).

Источник

Схемы замещения двухобмоточного трансформатора

Приведение вторичной обмотки к первичной

Первичные и вторичные токи, напряжения и другие величины имеют одинаковый порядок, если у первичной и вторичной обмоток число витков одинаково. Рассмотрим поэтому вместо реального трансформатора эквивалентный ему так называемый приведенный трансформатор, первичные и вторичные обмотки которого имеют одинаковое число витков.

Представим себе, что реальная вторичная обмотка трансформатора с числом витков w₂ заменена воображаемой, или приведенной, обмоткой с числом витков w₂’ = w₁. При этом число витков вторичной обмотки изменится в

раз. Величина k называется коэффициентом приведения или коэффициентом трансформации. Более подробно о том, что называется коэффициентом трансформации и как определить коэффициент трансформации изложено в статье «Принцип действия и виды трансформаторов».

В результате такой замены, или приведения, электродвижущая сила E₂’ и напряжение U₂’ приведенной обмотки также изменяются в k раз по сравнению с величинами E₂ и U₂ реальной вторичной обмотки:

Чтобы мощности приведенной и реальной обмоток при всех режимах работы были равны, необходимо соблюдать равенство

где I₂’ – приведенный вторичный ток. Отсюда с учетом второго равенства (2) следует, что

Намагничивающие силы приведенной и реальной обмоток на основании выражений (1) и (3) равны:

Для того чтобы электромагнитные процессы в реальном и приведенном трансформаторах протекали одинаково, приведенная и реальная вторичные обмотки должны создавать одинаковые магнитные поля. Для этого, кроме соблюдения условия (4), необходимо, чтобы приведенная вторичная обмотка имела те же геометрические размеры и конфигурацию и была расположена в окне магнитопровода трансформатора так же, как и реальная вторичная обмотка (смотрите например, рисунок 1, в статье «Магнитопроводы трансформаторов» и рисунок 1, в статье «Элементы конструкции и способы охлаждения масляных трансформаторов»). Поэтому суммарное сечение всех витков приведенной обмотки должно быть таким же, как и у реальной обмотки, а сечение каждого витка приведенной обмотки должно уменьшиться в k раз. Но поскольку приведенная обмотка имеет в k раз больше витков, то в итоге активное сопротивление приведенной обмотки в k 2 раз больше, чем реальной:

Так как при одинаковых геометрических размерах и одинаковом расположении катушек их индуктивности и индуктивные сопротивления пропорциональны квадратам чисел витков, то между индуктивными сопротивлениями приведенной обмотки x₂’ и реальной x₂ существует такое же соотношение:

Очевидно, что потери в приведенной и реальной обмотках одинаковы:

Одинаковы также относительные падения напряжения во вторичных обмотках приведенного и реального трансформаторов:

Таким образом, все энергетические и электромагнитные соотношения в приведенном и реальном трансформаторах одинаковы, что и позволяет производить указанное приведение.

Схема замещения без учета магнитных потерь

В соответствии с изложенным сделаем подстановки в уравнениях напряжения трансформатора (уравнения (2), представленные в статье «Уравнения напряжений трансформатора»):

что в математическом отношении соответствует переходу от исходных реальных переменных U₂, I₂ к новым (приведенным) переменным U₂’, I₂’. Умножив при этом второе из уравнений (2), представленное в статье «Уравнения напряжений трансформатора», на k, получим

При переходе к электрической связи двух цепей в соответствующей схеме замещения должна появиться общая для обеих цепей ветвь, которая обтекается суммой токов обеих цепей I₁ + I₂’. Соответственно этому в уравнениях напряжений этих цепей должны появиться одинаковые члены с множителями (I₁ + I₂’). Из уравнений (8) видно, что для получения в них таких членов нужно прибавить к первому из этих уравнений и вычесть из него член jkx₁₂ × I₁ и прибавить ко второму и вычесть из него член jkx₁₂ × I₂’. При этом получим

Введем следующие наименования и обозначения:

1) приведенное активное сопротивление вторичной обмотки

совпадающее с выражением (5);

2) приведенное взаимное индуктивное сопротивление

3) индуктивное сопротивление рассеяния первичной обмотки

4) приведенное индуктивное сопротивление рассеяния вторичной обмотки

представляет собой неприведенное индуктивное сопротивление рассеяния вторичной обмотки.

Введя перечисленные приведенные величины в уравнения (9), получим уравнения напряжения приведенного трансформатора:

Уравнениям (15), как нетрудно видеть, соответствует схема замещения рисунка 1, а. Действительно, мысленно обойдя левый и правый контуры схемы рисунка 1, а и составив уравнения напряжения для этих контуров, вновь получим уравнения (15). Таким образом, схема рисунка 1, а представляет собой схему замещения трансформатора, соответствующую уравнению (2), представленному в статье «Уравнения напряжений трансформатора» и уравнению (15), представленному в данной статье.

Аналогичным образом можно также преобразовать уравнения напряжения в дифференциальной форме (уравнения (1), представленные в статье «Уравнения напряжений трансформатора»), произведя в них подстановки

При этом получается схема замещения рисунка 1, б, где

представляют собой индуктивности рассеяния первичной и вторичной обмоток, а

Схема замещения рисунка 1, б действительна при любых закономерностях изменения напряжения и токов во времени, в том числе и в случае переходных процессов.

Уравнения (15) и схемы замещения рисунка 1 можно трактовать таким образом, что сопротивления r₁ и x₁, r₂’ и x₂’ или индуктивности S₁ и S₂’ включены в цепи обмоток до и после трансформатора, а параметры обмоток трансформатора уменьшены на значения этих величин. В результате получается идеальный трансформатор, активные сопротивления которого равны нулю, а коэффициент электромагнитной связи c = 1. Действительно, у такого идеального трансформатора приведенные собственные и взаимные индуктивные сопротивления одинаковы и равны x₁₂’ = k × x₁₂ и поэтому в соответствии с равенством (12), представленном в статье «Индуктивности обмоток трансформатора и электромагнитное рассеяние» и равенством (7), представленном в статье «Уравнения напряжений трансформатора», c₂ = 1 и σ = 0.

Отметим, что, как следует из рассмотрения приведенных преобразований, соотношения (7) и все последующие, а также схемы замещения рисунка 1 справедливы и правильно отражают все процессы в трансформаторе при любом значении k. С математической точки зрения эти преобразования означают переход от переменных U₂ и I₂ к новым переменным U₂’ и I₂’ по формулам (7), что возможно при любом значении k. В связи с этим необходимо подчеркнуть, что индуктивные сопротивления и индуктивности рассеяния, согласно равенствам (11) – (14), (17), (18) и (19), определяются неоднозначно и зависят от коэффициента приведения k. Однако для силовых трансформаторов k рационально определять по формуле (1), как это и принято на практике. Выбор иного значения k целесообразен лишь в специальных случаях, например в измерительных трансформаторах тока.

Параметры схемы замещения

Рассмотрим параметры схем замещения рисунка 1 при k = w₁ / w₂ [смотрите равенство (1)].
Приведенная взаимная индуктивность на основании равенств (6) и (10), в представленных статье «Индуктивности обмоток трансформатора и электромагнитное рассеяние» и равенства (19), настоящей статьи

Последний член выражения (20) весьма мал по сравнению с первым, и поэтому с достаточной точностью

Соответственно, согласно выражению (3), представленного в статье «Уравнения напряжений трансформатора» и выражениям (11), (19), (21), настоящей статьи,

Следовательно, сопротивление x₁₂’ с большой точностью равно сопротивлению самоиндукции первичной обмотки от потока, замыкающегося по магнитопроводу.

Ветви 1 – 2 схем замещения рисунка 1 называются намагничивающими ветвями. Протекающий по этим ветвям намагничивающий ток

создает результирующую намагничивающую силу обмоток трансформатора

которая в свою очередь создает результирующий поток стержня с амплитудой Ф_с. Напряжение на этих ветвях в соответствии с выражением (22), настоящей статьи и выражением (3), представленным в статье «Принцип действия и виды трансформаторов»

то есть равно по значению и обратно по знаку электродвижущей силе E₁, которая индуктируется в первичной обмотке результирующим потоком магнитопровода, или основным потоком трансформатора, и отстает от него на 90°.

Индуктивность рассеяния первичной обмотки, согласно выражениям (9) и (10), представленных в статье «Индуктивности обмоток трансформатора и электромагнитное рассеяние» и выражению (17), данной статьи,

Аналогично, согласно выражениям (9) и (10), представленных в статье «Индуктивности обмоток трансформатора и электромагнитное рассеяние» и выражению (18), данной статьи

Таким образом, индуктивности рассеяния S₁, S₂ и S₂’ и индуктивные сопротивления рассеяния при k = w₁ / w₂ определяются магнитными потоками, замыкающимися главным образом по воздуху.

Однако вторыми членами равенств (23) и (24) по сравнению с первыми пренебречь нельзя, и поэтому потоки, замыкающиеся по воздуху, можно назвать потоками рассеяния лишь условно.

Схема замещения с учетом магнитных потерь

Потери в стали магнитопровода p_мг при заданной частоте пропорциональны следующим величинам:

Таким образом, потери p_мг пропорциональны квадрату напряжения U₁₂ на зажимах 1 – 2 намагничивающей цепи схемы замещения рисунка 1, а. Если к этим зажимам параллельно x₁₂’ = x_c1 подключить активное сопротивление r_мг, как показано на рисунке 2, а, то потери в этом сопротивлении также будут пропорциональны U₁₂. Значение сопротивления r_мг можно подобрать так, чтобы потери в нем равнялись магнитным потерям:

Рисунок 2. Намагничивающая цепь схемы замещения с учетом магнитных потерь

Величину p_мг при заданной электродвижущей силе E₁ можно считать известной из расчетных (смотрите статью «Расчет магнитной цепи трансформатора») или опытных данных. Тогда можно считать известным также r_мг.

разделяется в двух ветвях намагничивающей цепи (рисунок 2, а) на активную I_мa и реактивную I_мr составляющие (смотрите статью «Расчет магнитной цепи трансформатора»), из, из которых первая определяет мощность магнитных потерь, а вторая создает поток магнитопровода.

Схема с двумя параллельными ветвями намагничивающей цепи хорошо согласуется с реальными физическими явлениями. Однако расчеты на основе схемы замещения вести удобнее, если объединить две параллельные ветви схемы 2, а в одну общую ветвь, как показано на рисунке 2, б. Тогда сопротивление этой ветви

При увеличении насыщения магнитопровода, то есть при увеличении Ф_с, E₁ или U₁, сопротивление x₁₂’ при f = const уменьшается. Однако при этом r_мг ≈ const, а значение r_м уменьшается.

Схема замещения трансформатора с учетом магнитных потерь согласно рисунку 2, б показана на рисунке 3, а. Если использовать обозначения

то схему замещения можно изобразить более компактно, как показано на рисунке 3, б. В режиме холостого хода I₂’ = 0 и I₁ = I_м – току холостого хода трансформатора.

В итоге получилась весьма простая Т-образная схема замещения трансформатора, представляющая собой пассивный четырехполюсник. Сопротивление намагничивающей цепи этой схемы Z_м отражает явления в ферромагнитном магнитопроводе. Оно значительно больше сопротивлений Z₁ и Z₂’, которые включают в себя активные сопротивления и индуктивные сопротивления рассеяния обмоток. Для силовых трансформаторов в относительных единицах

Уравнения напряжений и схему замещения трансформатора можно представлять также в относительных единицах. Имея в виду, что

левые части уравнений вида (15) можно разделить на U_н, а правые части – на Z_н × I_н, в результате чего и будет совершен переход к относительным единицам. Абсолютные значения U, I, r, x и Z в схемах замещения также можно заменить относительными. При этом расчеты режимов работы трансформатора можно вести в относительных единицах.

Нетрудно видеть, что относительные значения сопротивлений, токов и напряжений вторичной цепи будут зависеть от того, какая величина коэффициента k была использована при приведении вторичной обмотки к первичной. Неопределенность в этом вопросе исчезает, если определять k всегда одинаковым образом. Например, в силовых трансформаторах всегда берут k = w₁ / w₂.

Упрощенная схема замещения

При Z_м = ∞ и I_м = 0 схема замещения принимает вид, изображенный на рисунке 4. Параметры этой схемы

называются соответственно полным, активным и индуктивным сопротивлениями короткого замыкания. Такие названия обусловлены тем, что замыкание вторичных зажимов трансформатора накоротко соответствует замыканию накоротко вторичных (правых) зажимов схемы замещения рисунка 4 и при этом сопротивление трансформатора при коротком замыкании будет равным Z_к.

Схема замещения рисунка 4 чрезвычайно проста. Согласно этой схеме, трансформатор эквивалентен сопротивлению Z_к. Обычно в силовых трансформаторах z_к* = 0,05 – 0,15.

Источник: Вольдек А. И., «Электрические машины. Учебник для технических учебных заведений» – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.

Источник