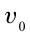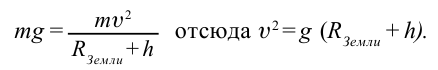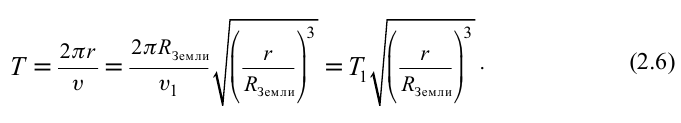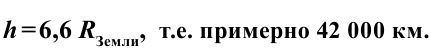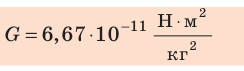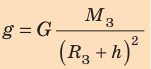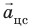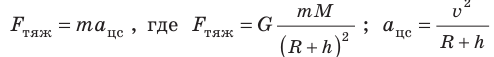движение в поле тяжести земли

Движение в поле тяжести земли

Рассмотрим некоторые примеры движения тел, когда единственная действующая на тело сила — это сила тяготения. В случаях, когда речь идет о движении брошенного камня или снаряда, выпущенного из пушки, поле тяготения Земли в пределах траектории можно считать однородным. При этом действующая на тело сила всюду одинакова и в соответствии со вторым законом Ньютона движение происходит с постоянным ускорением Фактически это соответствует приближению «плоской Земли», когда вектор ускорения всюду направлен одинаково, вертикально вниз, а его модуль принимается равным значению напряженности гравитационного поля вблизи поверхности Земли. Такое движение было подробно изучено ранее в главе, посвященной кинематике. Напомним, что траектория в этом случае представляет собой параболу с вертикальной осью симметрии.

Приближение «плоской Земли» справедливо лишь при сравнительно небольших скоростях, пока перемещение тела мало по сравнению с радиусом Земли. В противном случае необходимо учитывать изменение вектора напряженности гравитационного поля либо по модулю (при движении в радиальном направлении), либо по направлению (при движении вдоль поверхности шарообразной Земли), либо то и другое вместе.

Выясним сначала, возможно ли свободное движение тела параллельно земной поверхности. Очевидно, что в приближении «плоской Земли» это невозможно, так как параболическая траектория непременно пересечет плоскую поверхность Земли. Если же принять во внимание кривизну земной поверхности, то при некотором (достаточно большом) значении горизонтальной скорости движение вдоль поверхности становится возможным.

Рис. 94. Движение по низкой круговой орбите

Первая космическая скорость. В этом случае траектория тела представляет собой окружность, стелющуюся параллельно земной поверхности (рис. 94), а соответствующая скорость движения тела называется первой космической скоростью

Ее значение легко найти из условия, что в рассматриваемом случае в соответствии со вторым законом Ньютона центростремительное ускорение телу сообщает сила тяжести

Приведенное значение первой космической скорости получается при подстановке в формулу значения ускорения свободного падения и радиуса Земли км.

В действительности такое движение, разумеется, невозможно из-за сопротивления воздуха. Движение спутника Земли по круговой орбите возможно только тогда, когда орбита пролегает выше атмосферы. Самые низкие круговые орбиты спутников проходят на высоте более 100 км.

Круговая скорость. Скорость на такой круговой орбите радиуса называется круговой, и ее значение зависит от высоты орбиты над поверхностью Земли. Для ее определения в правую часть уравнения второго закона Ньютона (1) следует вместо подставить значение силы тяготения на расстоянии от центра Земли:

Формуле (4) можно придать другой, несколько более удобный вид, если выразить через ускорение свободного падения поверхности Земли: Тогда

С увеличением высоты орбиты круговая скорость уменьшается. Для высот , малых по сравнению с радиусом Земли выражение для можно упростить, используя приближенную формулу

В этом случае из (5) получаем

Из (6) видно, что для круговой орбиты на высоте, например, 200 км скорость меньше первой космической приблизительно на 1/64 ее часть, т. е. на 124 м/с.

Задачи

1. Расстояние до Луны. Звездный месяц, т. е. период Т обращения Луны вокруг Земли в гелиоцентрической системе отсчета, равен 27,32 суток. Зная радиус Земли км и ускорение свободного падения у ее поверхности найдите расстояние до Луны.

Решение. Считая, что Луна движется вокруг Земли по круговой орбите радиуса и применяя второй закон Ньютона к ее движению под действием силы притяжения к Земле, получаем, аналогично (5), для скорости Луны

Скорость связана с радиусом орбиты Луны и периодом обращения Т соотношением Подставляя ил в (7), находим

2. Плотность солнечного вещества. Зная радиус Солнца км, радиус земной орбиты км и период обращения Земли вокруг Солнца год, найдите среднюю плотность солнечного вещества. Найдите также минимально возможный период обращения спутника Солнца.

Решение. Применяя второй закон Ньютона к движению Земли по круговой орбите вокруг Солнца, аналогично (4) получаем

где — масса Солнца. Подставляя сюда значение скорости для массы Солнца находим

Отсюда для средней плотности солнечного вещества получаем

Минимальный период обращения был бы у спутника Солнца, обращающегося по орбите, стелющейся над его поверхностью, так как именно у такого спутника длина орбиты наименьшая, а скорость наибольшая. Это ясно и непосредственно из третьего закона Кеплера. Искомый минимальный период можно выразить через среднюю плотность солнечного вещества прямо из формулы (9), положив в ней

что составляет менее трех часов. Обратим внимание на то, что период обращения спутника по стелющейся орбите зависит только от средней плотности вещества, из которого состоит центральное притягивающее тело, и не зависит от его размеров.

Кеплерово движение. Круговое движение под действием ньютоновской силы притяжения представляет собой частный случай так называемого кеплерова движения, описываемого законами Кеплера. Чтобы спутник, поднятый на некоторую высоту, двигался по круговой орбите, ему нужно сообщить вполне определенную горизонтальную скорость. Если в какой-либо точке сообщить спутнику горизонтальную скорость, несколько большую круговой, он будет двигаться по эллиптической орбите, у которой данная точка будет перигеем, т. е. ближайшей к Земле точкой орбиты, а наиболее удаленная точка — апогей — будет лежать на противоположном конце прямой, проведенной из перигея через фокус эллипса, в котором находится центр Земли (рис. 95).

Рис. 95. Круговая и эллиптические орбиты при разных значениях начальной скорости

Рис. 96. Эллиптическая орбита в случае начальной скорости, меньшей круговой

Перигей и апогей находятся на противоположных концах большой оси эллипса.

Если же спутнику сообщить горизонтальную скорость, меньшую круговой, то он будет двигаться по эллиптической орбите, у которой начальная точка будет не перигеем, а апогеем, и, следовательно, центр Земли будет расположен в дальнем от нее фокусе эллипса (рис. 96). Периодическое движение по такой орбите возможно, разумеется, лишь тогда, когда она не пересекает поверхности Земли.

Существование замкнутых орбит — это замечательная особенность поля, в котором сила изменяется по закону обратных квадратов. Закономерности движения по эллиптическим орбитам будут подробнее рассмотрены после изучения законов сохранения.

Кроме замкнутых орбит в ньютоновском поле тяготения возможно движение по незамкнутым орбитам, когда тело приближается из бесконечности и, изменив направление движения под действием силы тяготения, снова уходит в бесконечность. Траектория в этом случае представляет собой гиперболу. Траектория, отделяющая замкнутые орбиты от незамкнутых, представляет собой параболу (эта парабола не имеет никакого отношения к параболе, по которой движется брошенное тело в приближении «плоской Земли»),

Конические сечения. Любое движение в поле тяготения как по замкнутым, так и по незамкнутым траекториям происходит по одному из так называемых конических сечений — кривых, которые получаются при пересечении кругового конуса с плоскостью (рис. 97).

Рис. 97. Конические сечения

В зависимости от наклона плоскости к оси конуса могут получиться окружность, эллипс, парабола и гипербола.

Незамкнутые траектории возможны не только тогда, когда тело приходит из бесконечности, но и тогда, когда ему сообщают достаточно большую начальную скорость в точке, находящейся на конечном расстоянии. Этот вопрос будет рассмотрен подробнее после изучения законов сохранения.

Сила тяжести внутри Земли. Закон обратных квадратов справедлив для поля тяготения, создаваемого точечной массой или шарообразным телом вне его пределов. Внутри шара поле тяготения будет совсем другим. Каким же именно? Будем, например, считать, что Земля представляет собой сплошной однородный шар. Выясним, как действующая на пробное тело сила тяжести зависит от его положения в стволе воображаемой шахты, прорытой от поверхности до центра Земли.

Очевидно, что в центре Земли эта сила равна нулю. Это непосредственно следует из симметрии: если бы сила вдруг оказалась

там отлична от нуля, то куда бы она была направлена? Ведь ни одному из направлений нельзя отдать предпочтение. Чтобы найти силу тяжести в произвольной точке на некотором расстоянии от центра Земли разобьем мысленно земной шар на тонкие сферические концентрические слои вокруг центра Земли (рис. 98). Согласно принципу суперпозиции полная сила тяжести, действующая на пробное тело на расстоянии от центра, равна векторной сумме сил, действующих на него со стороны отдельных концентрических слоев.

Рис. 98. К расчету силы тяготения на расстоянии от центра Земли

Легко убедиться в том, что сила тяготения, действующая со стороны любого слоя на тело, находящееся внутри этого слоя, равна нулю. Это сразу видно из построения, показанного на рис. 98. Малые части сферической оболочки с массами притягивают пробное тело массы с силами, пропорциональными этим массам и обратно пропорциональными квадратам расстояний Но сами массы как видно из рисунка, пропорциональны квадратам соответствующих расстояний. Действительно, показанные на этом рисунке треугольники подобны, а площади участков оболочки с массами пропорциональны квадратам их линейных размеров. В результате силы тяготения, действующие со стороны выделенных участков сферического слоя, уравновешиваются, что и доказывает сделанное утверждение, так как вся оболочка может быть разбита на такие пары элементов.

Подобными рассуждениями отсутствие силы тяготения внутри сферической оболочки было установлено еще Ньютоном.

Таким образом, на тело в стволе шахты в точке А (рис. 99) действует сила тяжести только со стороны заштрихованного шара, на поверхности которого находится это тело. Так как масса однородного заштрихованного шара пропорциональна кубу его радиуса а сила тяготения пропорциональна массе и в то же время обратно пропорциональна квадрату радиуса, то эта сила в конечном счете оказывается просто пропорциональна радиусу шара: . Коэффициент пропорциональности проще всего найти, учитывая, что на поверхности Земли, когда сила тяжести равна . На произвольном расстоянии от центра при очевидно,

Так как при сила тяжести убывает обратно пропорционально квадрату расстояния, график зависимости силы тяжести имеет вид, показанный на рис. 100.

Совсем иной характер зависимости силы тяготения от внутри Земли означает, что при движении тела со скоростью, меньшей круговой, движение по пересекающей Землю эллиптической траектории с дальним фокусом в центре Земли невозможно, даже если прорыть туннель вдоль этой траектории и выкачать из него воздух.

Рис. 99. Сила тяготения в точке А обусловлена действием только заштрихованной части земного шара

Рис. 100. Зависимость силы тяготения от расстояния до центра Земли

• Современные астрономические средства наблюдений позволяют измерить скорость разных участков кольца планеты Сатурн. Можно ли из таких наблюдений установить, является ли кольцо сплошным?

• Почему из наблюдений за движением планеты под действием силы притяжения к Солнцу невозможно определить ее массу? Как найти массу планеты по наблюдениям за ее спутниками?

• Когда телу над Землей сообщена горизонтальная скорость, меньшая круговой, то, как было сказано, оно движется по траектории, представляющей собой часть эллипса с дальним фокусом в центре Земли. Как согласовать этот факт с известным утверждением, что брошенное горизонтально тело движется в поле тяжести Земли по параболе?

• Может ли прилетевший из бесконечности метеор, не задевший земной атмосферы, стать спутником Земли?

• Как стало бы двигаться тело, которое уронили в воображаемый туннель, прорытый по диаметру Земли?

• Решите задачу 1, учитывая, что в действительности Земля и Луна обращаются вокруг их общего центра масс.

Источник

Содержание:

Движение в гравитационном поле:

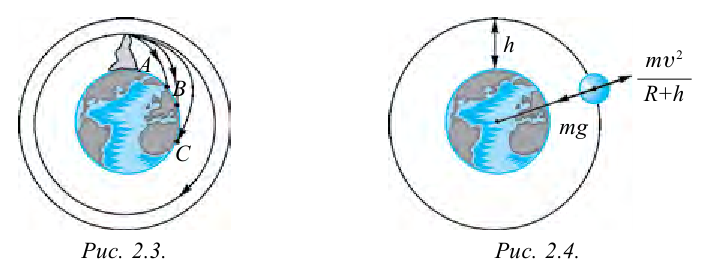
Вы в 7-ом классе узнали о том, что Земля создает вокруг себя постоянное поле притяжения и с помощью этого поля притягивает к себе все тела. Значит, на любое движение на Земле оказывает свое влияние поле притяжения. Представим, что с вершины горы брошено какое-либо тело в горизонтальном направлении со скоростью

Если скорость тела увеличить, то оно упадет в точке или . Начиная с некоторой определенной скорости тела не падают на Землю, а начинают вращаться вокруг Земли. Такое тело становится искусственным спутником Земли. Движение искусственного спутника является движением в поле притяжения. Почему спутник не падает на Землю? При каких скоростях
это происходит? Сначала рассмотрим силы, действующие на спутник. На спутник постоянно действует сила притяжения Земли. Чтобы снизить сопротивление воздуха, спутник нужно поднять в самые верхние слои атмосферы.

На высоте 300 – 400 км от поверхности Земли сопротивление воздуха почти отсутствует. Значит, на таких высотах силу притяжения Земли компенсирует центробежная сила, которая появляется благодаря скорости спутника (рис. 2.4).
В этом случае:

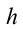
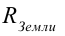
В случае, когда высоту по сравнению с радиусом Земли можно не учитывать,

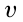
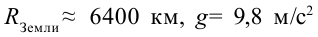
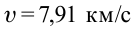
Чтобы вычислить значение , принимаем , соответственно .
Эта скорость называется первой космической скоростью.
Искусственный спутник Земли, который двигается с такой скоростью, делает один оборот вокруг Земли за время: .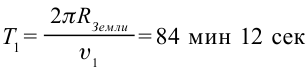

На практике время, за которое спутник совершает один оборот, больше чем расчетное время. Причина этого явления в том, что радиус орбиты спутника и радиус Земли отличаются друг от друга.

Таким образом, скорости спутников, вращающихся на орбитах с большими радиусами, будут меньше, чем скорости спутников, вращающихся на орбитах, близких к поверхности Земли.

Период вращения таких спутников вычисляется по формуле:

Здесь: 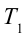– период вращения спутников, вращающихся на орбитах, близких к поверхности Земли.

Используя формулу периода вращения спутника, вращающегося на произвольных высотах, можно вычислить необходимое расстояние от Земли, на котором спутник должен зафиксироваться. На какой высоте должен двигаться спутник, чтобы период его вращения был равен 24 часам? Расчеты показали, что высота составляет:

Такая орбита называется геостационарной орбитой.

Впервые на нашей планете 4 октября 1957 года на территории бывшего СССР был запущен первый искусственный спутник Земли. Спутник имел форму шара диаметром 58 см и массой 83,6 кг. Этот спутник совершил вокруг Земли 1400 оборотов, т.е. преодолел расстояние в 60 миллионов километров. А 12 апреля 1961 года первый человек полетел в космос. Первый космонавт Юрий Алексеевич Гагарин был гражданином бывшего СССР. 20 июля 1969 года американские астронавты Нейл Армстронг и Эдвин Олдрин впервые совершили посадку на Луну.

Для того чтобы долететь до планет Солнечной системы, космический корабль должен преодолеть вторую космическую скорость, равную 11,2 км/с.
Для достижения далеких звезд потребуется преодолеть силу притяжения Солнечной системы, т.е. космический корабль должен двигаться с третьей космической скоростью. Величина третьей космической скорости равна 16,7 км/с.

Среди космонавтов, которые многократно летали в космос, наш соотечественник В. Джанибеков и представитель узбекской нации С. Шарипов.

Гравитационное поле и сила притяжения

Шесть из восьми планет Солнечной системы были открыты благодаря наблюдениям за звездным небом. Именно так в 1781 г. английский астроном Джон Гершель открыл Уран. Впрочем, планета вела себя «странно»: ее орбита не соответствовала расчетам, основанным на законе всемирного тяготения. Ученые предположили, что рядом с Ураном есть еще одна планета, и начали искать ее с помощью. математики.

Рассчитать орбиту новой планеты удалось англичанину Джону Адамсу и французу Урбену Леверье. 23 августа 1846 г. немецкий астроном Иоганн Галле навел телескоп на указанное Леверье место и. увидел планету! Нептун — восьмая планета Солнечной системы — стал первым космическим объектом, открытым «на кончике пера».

Как определить силу гравитационного притяжения

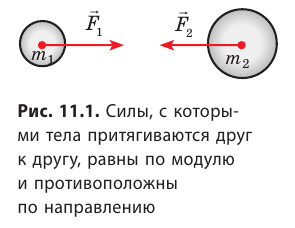
Гравитационное взаимодействие — взаимодействие, свойственное всем телам во Вселенной и проявляющееся в их взаимном притяжении друг к другу. Гравитационное взаимодействие происходит посредством гравитационного поля, которое существует вокруг любого тела: звезды, планеты, человека, молекулы и т. д. Выведем закон всемирного тяготения, следуя логике рассуждений Ньютона, который и установил данный закон.

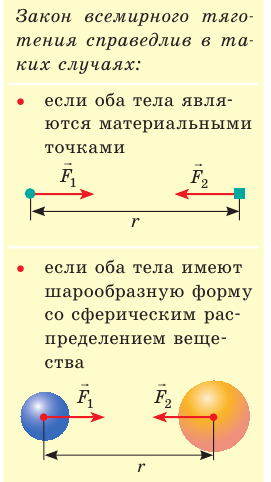
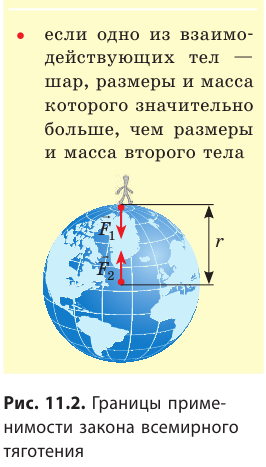
Закон всемирного тяготения имеет определенные границы применимости (рис. 11.2). Только в XX в. было установлено: когда гравитационные поля настолько сильны, что разгоняют тела до скоростей порядка скорости света, или когда частицы, пролетающие вблизи массивных тел, еще на отдалении имеют скорость, сравнимую со скоростью света, силу гравитационного притяжения нельзя рассчитать по закону всемирного тяготения. В общем случае тяготение описывается общей теорией относительности.

Как измерить гравитационную постоянную

Гравитационная постоянная G — одна из фундаментальных констант в физике. По современным данным, значение гравитационной постоянной составляет:

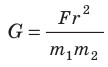
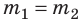
Из формулы (3) следует: . То есть, если r= 1 м, а =1 кг, то G численно равна F. Гравитационная постоянная численно равна силе гравитационного притяжения двух материальных точек массой 1 кг каждая, находящихся на расстоянии 1 м друг от друга.

Измерить гравитационную постоянную достаточно сложно: гравитационное притяжение между телами становится заметным только при очень большой массе хотя бы одного из тел.

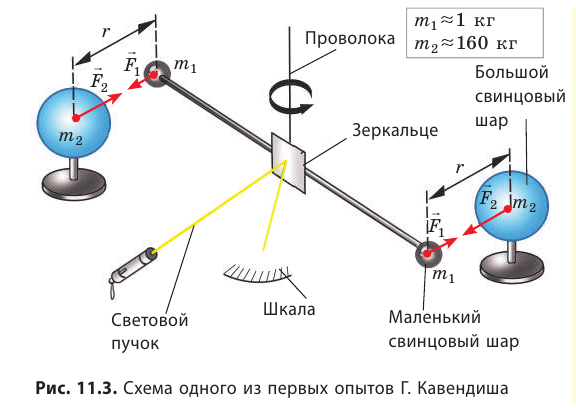
Гравитационную постоянную впервые измерил английский ученый Генри Кавендиш (1731–1810) в 1798 г. с помощью крутильных весов (рис. 11.3).

Как «взвесить» Землю

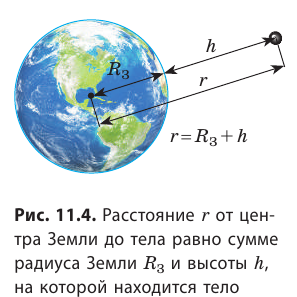
Опыт Г. Кавендиша еще называют «взвешиванием Земли». Как можно измерить массу Земли и любой другой планеты? Вспомним о силе тяжести.

Сила тяжести 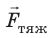— это сила, с которой Земля (или другое астрономическое тело) притягивает к себе тела, находящиеся на ее поверхности или вблизи нее.

Сила тяжести направлена вертикально вниз и приложена к точке, которую называют центром тяжести тела.

Приравняв правые части формул (1) и (2), получим формулу для вычисления ускорения свободного падения:

Проанализировав последнюю формулу, приходим к следующим выводам.

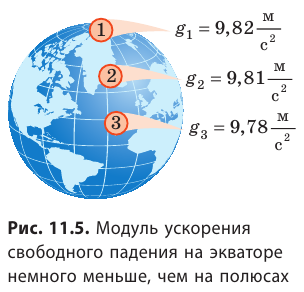
Отметим, что из-за вращения Земли, а также из-за того, что форма Земли — геоид, ускорение свободного падения зависит от географической широты местности (рис. 11.5).

Ускорение свободного падения в определенной местности может отличаться от его средних значений на данной широте. Причины — в неоднородности земной коры, наличии гор и впадин; в различной плотности пород, залегающих в недрах Земли. Так, уменьшение ускорения свободного падения часто свидетельствует о залежах торфа, нефти, газа; увеличение — о залежах металлических руд. Метод поиска залежей полезных ископаемых по точному определению ускорения свободного падения называют гравиметрической разведкой.

Первая космическая скорость

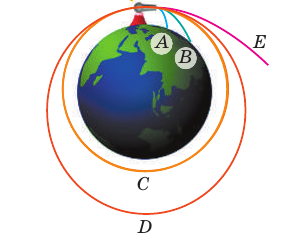
Представим, что мы стреляем из пушки в горизонтальном направлении, с каждым выстрелом увеличивая скорость движения ядра. Траектория движения ядер будет параболической, и каждый раз ядра будут падать все дальше. Если представить, что Земля плоская, на этом наш эксперимент можно было бы и завершить, но Земля имеет форму шара, поэтому с каждым выстрелом она все больше и больше будет «уходить» из-под ядра (рис. 11.6). Теперь представим, что сопротивление воздуха отсутствует, а мы придали ядру такую большую скорость, что оно облетело вокруг Земли и вернулось к месту выстрела.

При этом ядро не остановится, а будет и дальше двигаться с неизменной скоростью, «наматывая круги» вокруг планеты. Другими словами, мы получим искусственный спутник Земли.

Рис. 11.6. Движение тела под действием силы тяжести (по рисунку И. Ньютона): ядра A и B падают на Землю, ядро C выходит на круговую орбиту, D — на эллиптическую, ядро E летит в открытый космос

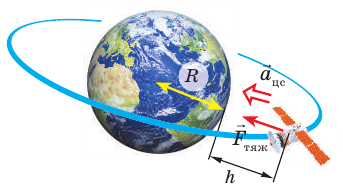
Рис. 11.7. На спутник, движущийся по круговой орбите на высоте h над поверхностью планеты, действует одна сила — сила тяжести 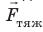, которая и придает спутнику центростремительное ускорение

Скорость, которую надо сообщить объекту, чтобы он двигался вокруг планеты по круговой орбите, называют первой космической скоростью.

Первую космическую скорость v можно вычислить, учитывая, что именно сила тяжести придает телу центростремительное ускорение (рис. 11.7). По второму закону Ньютона:

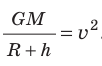
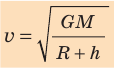
Следовательно, . Отсюда получаем формулу для вычисления первой космической скорости движения спутника на высоте h над поверхностью планеты: .

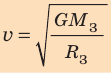
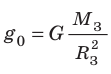
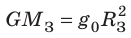
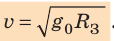
Для случаев вблизи поверхности Земли (h≈ 0) данная формула принимает вид: . Вспомним, что у поверхности Земли, то есть . После упрощения получим: .

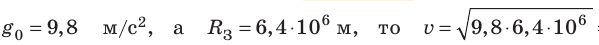
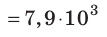
Поскольку =(м/с) — первая космическая скорость у поверхности Земли.

4 октября 1957 г. Советский Союз вывел на орбиту первый искусственный спутник Земли — ПС-1. Его разработали С. П. Королев, М. В. Келдыш, М. К. Тихонравов и другие выдающиеся ученые. ПС-1 представлял собой небольшую сферу диамет ром 58 см и массой 83,6 кг, оснащенную четырьмя антеннами длиной 2,4 и 2,9 м для передачи сигнала.

Спутник отделился от второй ступени ракеты-носителя на 315-й секунде после старта и почти сразу начал передавать сигнал, который слышали не только специалисты, но и радиолюбители практически всех стран. С этого момента начался отсчет космической эры человечества.

«Тот маленький огонек, стремительно двигающийся от края и до края неба. сделал человечество бессмертным», — писал американский писатель-фантаст Рэй Брэдбери. В течение 92 суток полета спутник совершил 1440 оборотов вокруг Земли, после чего сгорел в атмосфере. Траекторию движения спутника на карту звездного неба первыми нанесли наблюдатели Лаборатории космических исследований Ужгородского государственного университета.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник