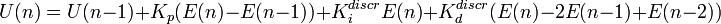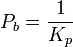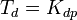движение вдоль стены трик

Движение вдоль стены трик

пятница, 26 ноября 2010 г.

Алгоритмы: движение вдоль стены

Не правда ли программа, заданная в качестве задачки на понимание NXT-G в этом посте, похожа на программы, поясняющие движение вдоль линии, в этом?

Если быть более точным, то в задаче робот поворачивает вправо, если расстояние на сенсоре меньше 14 см. и влево, если расстояние на сенсоре больше 16 см. Сложно представить, для чего может понадобиться такое движение, если сенсор смотрит вперед или назад. Но многое встает на свои места, если предположить, что сенсор установлен на одном из бортов робота и смотрит в сторону.

Если нарисовать схему такого движения, то становится видно, что по левому борту робота на протяжении всего движения, находится какое-то препятствие и робот пытается не подъезжать к нему слишком близко и не отъезжать слишком далеко. Если предположить, что препятствие это стена, то движение робота можно назвать движением вдоль стены. При некрутых заворотах стены, робот будет стараться держаться на определенном расстоянии, т.е. поворачивать вместе с заворотом стены.

Кстати, этот вариант ответа (движение вдоль стены) тоже был среди ответов, которые были присланы после публикации задачи.

Как и с предложенным алгоритмом движения вдоль линии, следует помнить, что данная реализация движения вдоль стены тоже является базовой для изучения. Т.е. при решениях реальных задач, алгоритм движения будет значительно сложнее, но принцип движения останется тот же.

Сейчас же хотелось бы обратить внимание на одну деталь, об которую довольно часто «спотыкаются» те, кто только начинает реализовывать дивжение вдоль стены.

Источник

Движение по линии

Рассмотрим простейший алгоритм движения по черной линии на одном датчике цвета на EV3.

Данный алгоритм является самым медленным, но самым стабильным.

Робот будет двигаться не строго по черной линии, а по ее границе, подворачивая то влево, то вправо и постепенно перемещаясь вперед.

Алгоритм очень простой: если датчик видит черный цвет, то робот поворачивает в одну сторону, если белый — в другую.

Реализация в среде Lego Mindstorms EV3

В обоих блоках движения выбираем режим «включить». Переключатель настраиваем на датчик цвета — измерение — цвет. В нижней части не забудьте изменить «нет цвета» на белый.

Также, необходимо правильно указать все порты.

Не забудьте добавить цикл, без него робот никуда не поедет.

Проверьте. Для достижения лучшего результата попробуйте изменить значения рулевого управления и мощности.

Алгоритм:

Действие алгоритма основано на том, что в зависимости от степени перекрытия, пучка подсветки датчика чёрной линией, возвращаемые датчиком показания градиентно варьируются. Робот сохраняет положение датчика света на границе чёрной линии. Преобразовывая входные данные от датчика света, система управления формирует значение скорости поворота робота.

Более устойчиво алгоритм работает, если использовать моторы с управлением скоростью –100. 100.

В этом случае есть возможность отрегулировать плавность поворота в соответствии с кривизной линии

Источник

Робототехника ТРИК. Движение вдоль стены

Движение вдоль стены с мячами созданные на платформе TRIK Studuo. #trikset, #TRIKStuduoПодробнее

Движение вдоль стены созданное в среде программирования TRIK Studuo. #trikset, #TRIKStuduoПодробнее

Движение робота вдоль стены с мячами и банками. Программирование в TRIK Studuo. #TRIKStuduoПодробнее

Движение по линии с одним датчиком света в программе TRIK STUDIOПодробнее

Движение вдоль стены (П-регулятор)Подробнее

Урок 11. Элементы навигацииПодробнее

Урок 1. Элементарные действия / Программирование в TRIK StudioПодробнее

П-регулятор. Движение по линии с одним датчиком светаПодробнее

ПД- регулятор для движения вдоль контрастной линии. Практика (Lego EV3, Small Basic).Подробнее

Робототехника ТРИК: движение по линии с двумя датчиками освещенностиПодробнее

Движение по линии, П-регулятор. Программирование Lego Maindstorms EV3Подробнее

Часть 3. ТРИК StudioПодробнее

Движение по кругу программирование LEGO EV3Подробнее

Урок 11. Элементы навигации / Программирование в TRIK StudioПодробнее

Движение робота вдоль стенкиПодробнее

Дистанционная робототехника. ПД-регулятор в TRIK studioПодробнее

8. УЛЬТРАЗВУКОВОЙ ДАТЧИК LEGO EV3 Classroom 2021. Программирование с нуляПодробнее

прохождение лабиринта в TRIK StudioПодробнее

Использование датчика касания в TRIK StudioПодробнее

Источник

Движение вдоль стены робота кратко

ПИД-регулятор

Пропорционально-интегрально-дифференциальный (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трех слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования.

Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегральным,пропорционально-дифференциальным, пропорциональным и т. п.

Общие сведения

Пропорциональная составляющая

Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю.

Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления, при наличии задержек в системе, могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.

Интегральная составляющая

Интегральная составляющая пропорциональна интегралу от отклонения регулируемой величины. Ее используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку.

Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечивать интегральная составляющая. Тем не менее, интегральная составляющая также может приводить к автоколебаниям.

Дифференциальная составляющая

Дифференциальная составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему.

Теория

Выходной сигнал регулятора u определяется тремя слагаемыми:Назначение ПИД-регулятора — в поддержании заданного значения x₀ некоторой величины x с помощью изменения другой величины u. Значение x₀ называетсязаданным значением (или уставкой, в технике), а разность e = (x₀ − x) — невязкой (или ошибкой [регулирования], в технике), рассогласованием или отклонением величины от заданной.

,

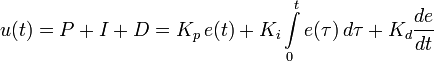
где К_p, К_i, К_d — коэффициенты усиления пропорциональной, интегральной и дифференциальной составляющих регулятора, соответственно.

Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегральная и дифференциальная составляющие:

В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму:

,

В программной реализации для оптимизации расчетов переходят к рекуррентной формуле:

Часто в качестве параметров ПИД-регулятора используются:

Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов.

Ссылки

Не правда ли программа, заданная в качестве задачки на понимание NXT-G вэтом посте, похожа на программы, поясняющие движение вдоль линии, в этом?

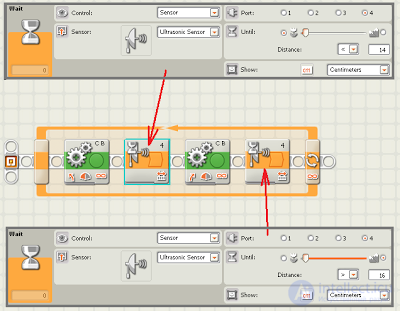
Если быть более точным, то в задаче робот поворачивает вправо, если расстояние на сенсоре меньше 14 см. и влево, если расстояние на сенсоре больше 16 см. Сложно представить, для чего может понадобиться такое движение, если сенсор смотрит вперед или назад. Но многое встает на свои места, если предположить, что сенсор установлен на одном из бортов робота и смотрит в сторону.

Если нарисовать схему такого движения, то становится видно, что по левому борту робота на протяжении всего движения, находится какое-то препятствие и робот пытается не подъезжать к нему слишком близко и не отъезжать слишком далеко. Если предположить, что препятствие это стена, то движение робота можно назвать движением вдоль стены. При некрутых заворотах стены, робот будет стараться держаться на определенном расстоянии, т.е. поворачивать вместе с заворотом стены.

Кстати, этот вариант ответа ( движение вдоль стены ) тоже был среди ответов, которые были присланы после публикации задачи.

Как и с предложенным алгоритмом движения вдоль линии, следует помнить, что данная реализация движения вдоль стены тоже является базовой для изучения. Т.е. при решениях реальных задач, алгоритм движения будет значительно сложнее, но принцип движения останется тот же.

Сейчас же хотелось бы обратить внимание на одну деталь, об которую довольно часто «спотыкаются» те, кто только начинает реализовывать дивжение вдоль стены.

Решение этой проблемы, традиционно, не одно. Оно может быть как программным, так и конструкторским. Например, можно не фиксировать датчик жестко, а поставить его на мотор.

Таким образом, после поворота робота, скажем, налево, сенсор расстояния поворачивается, стараясь быть направленным прямо на стену. А при повороте направо, мотор поворачивает сенсор в другую сторону:

Особенно такая схема удобна при сборке робота с управляющимим рулевым мотором, тогда сенсор можно крепить к тому же мотору, что управляет направляющими колесами. Причем лучше крепить не напрямую, а подобрать подходящее сочетание шестерней.

5.1.7. Движение вдоль стенки

Расстояние до стенки в настоящий момент времени, которое показывает датчик, обозначим .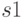

Моторы двигаются со средней скоростью 50, но при отклонении от заданного курса на них осуществляется управляющее воздействие up. Снова обозначим это следующим образом.

Осталось определить, чему будет равно управляющее воздействие. Это нетрудно:

Таким образом, при робот не меняет курса и едет прямо. В случае отклонения его курс корректируется. Здесь — это некоторый усиливающий коэффициент, определяющий воздействие регулятора на систему. Для робота NXT средних размеров коэффициент k может колебаться от 1 до 10 в зависимости от многих факторов. Предлагаем подобрать его самостоятельно.

В данном случае регулятор будет эффективно работать только при малых углах отклонения. Кроме того, движение практически всегда будет происходить по волнообразной траектории. Сделать регулирование более точным позволит введение новых принципов, учитывающих отклонение робота от курса.

5.1.8. Пропорционально-дифференциальный регулятор

В некоторых ситуациях П-регулятор может вывести систему из устойчивого состояния. Например, если робот направлен от стенки, но находится к ней ближе заданного расстояния, на моторы поступит команда еще сильнее повернуть от стенки, в результате чего с ней может быть утерян контакт (напоминаем, что датчик расстояния получает отраженный сигнал практически только от перпендикулярной поверхности).

Для защиты от подобных ситуаций добавим в регулятор дифференциальную составляющую, которая будет следить за направлением движения робота. Иными словами, вектор скорости будет влиять на управляющее воздействие. Известно, что скорость находится как , где — это изменение расстояния за промежуток времени . Определим дифференциальный регулятор через скорость отклонения робота от заданного положения:

где — текущее расстояние до стенки, — расстояние на предыдущем шаге.

Поскольку замеры производятся через равные промежутки времени, то можно принять за константу.

Таким образом, ПД-регулятор описывается формулой из двух слагаемых

Можно показать, что для устойчивого достижения цели коэффициент при дифференциальной составляющей должен превышать (см. ниже статью «Элементы теории автоматического управления в школе»).

Алгоритм движения вдоль стенки на ПД-регуляторе в целом будет выглядеть так:

Для объезда предметов потребуется ввести контроль показаний датчика расстояния: при резком изменении робот должен делать вывод о возможном повороте, который надо будет производить с другими коэффициентами.

А как ты думаешь, при улучшении движение вдоль стены, будет лучше нам? Надеюсь, что теперь ты понял что такое движение вдоль стены и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Робототехника

Источник

Робот движение вдоль стены

С глубокой древности лабиринты несли ощущение тайны и загадки. Один из первых лабиринтов, известных человечеству, описывает Геродот — это был египетский Лабиринт, в котором было 5000 комнат. Со временем лабиринты утратили свое религиозно-мистическое значение и стали объектами развлечений, превратившись в сады и парки в виде зеленых изгородей сложной конфигурации.

Разгадывание лабиринтов всегда являлось увлекательнейшим занятием, но еще более увлекательным является создание машин, способных пройти Лабиринт.

Одним из самых простых правил для прохождения лабиринта является правило «одной руки»: двигаясь по лабиринту, надо все время касаться правой или левой рукой его стены. Этот алгоритм, вероятно, был известен еще древним грекам. Придется пройти долгий путь, заходя во все тупики, но в итоге цель будет достигнута. Хотя у этого правила и есть один недостаток, но о нем мы поговорим позже.

Попробуем описать робота, действующего в соответствии с правилом «правой руки».

В начале своей работы робот должен найти стену, по которой он будет следовать. Для этого он может просто двигаться вперед, пока не упрется в преграду.

После того как робот наткнулся на препятствие, он начинает передвигаться в соответствии с правилом «правой руки».

Двигаясь вдоль стены, робот следит, есть ли проход справа. Если проход есть, робот должен идти по нему, чтобы не оторваться от стены справа.

Если прохода нет — впереди стена — робот поворачивает налево. Если прохода снова нет, он еще раз поворачивает налево, таким образом разворачиваясь на 180 градусов, и идет в обратном направлении.

Блок-схема алгоритма для робота, работающего по правилу «правой руки», представлена на рисунке.

Диалект языка Лого, который мы будем использовать, очень прост и похож на Basic. Познакомиться с командами языка можно здесь. А бесплатно скачать среду программирования GameLogo — здесь. Размер дистрибутива невелик — всего 1 Mb.

В архиве с GameLogo есть фоны с лабиринтами, одним из которых мы и воспользуемся.

В самом начале программы дадим команду черепахе, чтобы она подняла перо (по умолчанию черепаха оставляет после себя след).

Размер поля — 800 на 600 точек. Исходное положение для черепахи находится в месте с координатами 115, 545 (белый квадрат).

Цвет дорожек лабиринта — светлый, на них датчик будет принимать значения больше 50. Цвет стен лабиринта — темный, значение датчика будет меньше 50. Выход из лабиринта представлен черным квадратом, значение датчика над которым будет равно 0.

Объявим переменную флаг, с помощью которой будем контролировать, достигнут ли выход из лабиринта.

Напишем программу и запустим ее с помощью большой красной кнопки с надписью «Выполнить».

Если известно, что у лабиринта нет отдельно стоящих стенок, то есть нет замкнутых маршрутов, по которым можно возвращаться в исходную точку, то такой лабиринт называют односвязным и его всегда можно обойти полностью, применив правило «одной руки».

Если же лабиринт содержит отдельно стоящие стенки, то, применяя правило «одной руки», не всегда можно пройти все коридоры и тупики. Лабиринты с отдельно стоящими стенками и с замкнутыми маршрутами называются многосвязными. При этом многосвязные лабиринты можно разделить на две группы: без «петли» вокруг цели (замкнутый маршрут не проходит вокруг цели) и с замкнутой «петлей» вокруг цели (цель можно обойти по замкнутому маршруту).

В многосвязных лабиринтах второй группы правило «одной руки» не работает и, применяя его, достичь цели невозможно. Но и эти лабиринты можно пройти, полагаясь на точный алгоритм.

Решение задачи о таких лабиринтах принадлежит сравнительно позднему времени, и начало ему положено Леонардом Эйлером. Эйлер не без оснований полагал, что выход из любого лабиринта может быть найден, и притом сравнительно простым путем.

Тремо предлагает следующие правила: выйдя из любой точки лабиринта, надо сделать отметку на его стене (крест) и двигаться в произвольном направлении до тупика или перекрестка; в первом случае вернуться назад, поставить второй крест, свидетельствующий, что путь пройден дважды — туда и назад, и идти в направлении, не пройденном ни разу, или пройденном один раз; во втором — идти по произвольному направлению, отмечая каждый перекресток на входе и на выходе одним крестом; если на перекресте один крест уже имеется, то следует идти новым путем, если нет — то пройденным путем, отметив его вторым крестом.

Зная алгоритм Тремо, можно скорректировать поведение легендарного Тесея. Вдохновленный подарком любимой Ариадны, он уверенно идет по лабиринту. Вдруг перед ним возникает ход, по которому уже протянута нить. Что делать? Ни в коем случае не пересекать ее, а вернуться по уже известному пути, сдваивая нить, пока не найдется еще один непройденный ход.

Применив вариант алгоритма Тремо, отец теории информации Клод Шеннон (Claude Elwood Shannon) построил одного из первых самообучающихся роботов. Шеннон дал ему звучное имя «Тесей», но в истории «Тесей» стал больше известен как «мышь» Шеннона. «Мышь» сначала обследовала весь лабиринт, а затем (во второй раз) проходила весь путь значительно быстрее, избегая участков, пройденных дважды.

В наши дни роботы, проходящие лабиринт, являются участниками одного из самых интересных состязаний думающих машинок, которое проходит в нескольких странах мира. Эти соревнования носят общее название Micromouse competition и по своим техническим новациям относятся к лидерам робототехнического спорта.

На первой Российской Олимпиаде Роботов проводились соревнования, целью которых было прохождение своеобразного лабиринта: за наиболее короткое время, двигаясь через «открытые двери» в стенках, робот должен был добраться от места старта до места финиша. Контролировать свое движение робот мог по черным линиям, нанесенным на пол лабиринта.

Релейный регулятор

Пример 9.1. Движение робота вдоль стены.

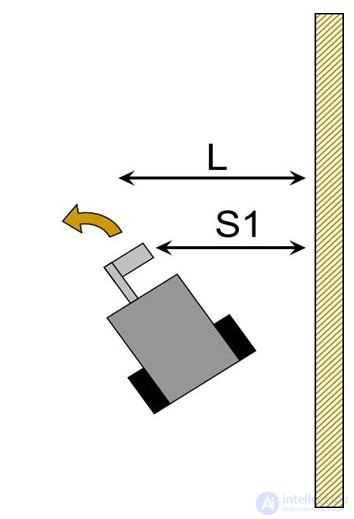
Пусть имеется робот, оснащённый датчиком ультразвука, и не очень ровная стена (с небольшими выступами и впадинами). Требуется написать программу управления движением робота вдоль стены на заданном расстоянии.

Следует заранее продумать положение датчика ультразвука. Как упоминалось выше (см. с. 38), этот датчик медленный. Поэтому его следует располагать чуть впереди корпуса робота. Кроме этого, его следует сместить как можно дальше от стены (см. Рис. 9.1), потому что на малых расстояниях (5 — 7 см) показания датчика ультразвука становятся слишком неточными. Далее мы увидим, что направление датчика также следует подкорректировать.

Алгоритм движения робота, записанный в словесной форме, может быть примерно таким (Рис. 9.2):

Одним из самых очевидных решений этой задачи является релейный регулятор.

Для определённости примем в качестве заданного расстояния 20 см. Получим следующую программу (Рис. 9.3):

Как видно из текста программы, после включения обоих моторов запускается бесконечный цикл, в котором реализован вышеописанный словесный алгоритм. Хорошо заметной особенностью этого подхода является «рыскающее» движение: робот всегда поворачивает с одной и той же интенсивностью, независимо от того, насколько далеко или близко он оказался по отношению к стене. Поэтому траектория всегда будет зигзагообразной, так как во время поворотов робот всегда будет «прыгать» вокруг среднего значения 20 см. Так как датчик ультразвука является «медленным», в цикле используется небольшая задержка (0,1 с) для того, чтобы показания датчика успевали обрабатываться блоком NXT. Величина задержки фактически определяет время, в течение которого робот будет двигаться в неизменном направлении. Другими словами, увеличивая время задержки мы получим более крупные «зубцы» траектории. Как отмечалось ранее, делать задержку меньше 0,06 с не имеет смысла, потому что в этом случае датчик ультразвука просто не успеет провести измерения.

При использовании релейного регулятора возможны частые уходы робота с дистанции. Одна из причин состоит в том, что при выбранном нами расположении датчика ультразвука робот не сможет различать положения, симметричные относительно нормального положения. То есть два положения, показанные на Рис. 9.4 будут идентичными, и расстояние до стены в обоих случаях окажутся больше 20 см. В соответствии с вторым шагом алгоритма робот должен повернуть к стене (влево). И если для второго положения это верно, то для первого — ошибочно: робот ещё больше уйдёт с трассы.

Эту проблему можно решить, если расположить датчик не перпендикулярно к направлению движения (т. е. строго влево), а под углом 45° к направлению движения (Рис. 9.5).

Так нам удастся избежать случая, показанного на Рис. 9.4. Действительно, при подруливании влево расстояние до стены будет (при небольших углах поворота U(t) на моторы робота в момент времени t вычисляется по формуле:

Очевидно, графиком для расчёта управляющего воздействия U в зависимости от ошибки E будет прямая (см. Рис. 9.6):

Ошибка может быть как положительная (если мы ближе к стене, чем надо), так и отрицательная (если мы отъехали от стены дальше, чем необходимо). Таким образом, управляющее воздействие U(t) тоже может быть как положительным, так и отрицательным.

Пусть мы имеем P-регулятор для робота, движущегося вдоль стены. Тогда мощность моторов PowerB(t) и PowerC(t) в момент времени t вычисляется по формулам:

Реализуем алгоритм P-регулятора согласно приведённым формулам при помощи вложенных процедур ( My blocks ) на языке NXT-G.

Блок Error на языке NXT-G выглядит так:

Этот блок мы используем для разработки блока P-регулятора. Он будет иметь следующие параметры:

Наконец, полная программа, реализующая бесконечное движение вдоль стены, получается с использованием блока P-регулятора и формул (9.2) и (9.3):

Задание 9.4. Реализуйте предложенный алгоритм движения вдоль стены с использованием P-регулятора. Проверьте его работу. Настройте регулятор при помощи подбора коэффициента .

Задание 9.5. Реализуйте алгоритм следования по линии с использованием P-регулятора. Настройте регулятор, добиваясь наиболее уверенного прохождения роботом крутых поворотов.

Задание 9.6. Проведите соревнование в своей группе да скоростное прохождение трассы.

Задание 9.7. После того, как робот стал двигаться по линии более или менее уверенно, попробуйте (1) увеличить подобранный коэффициент вдвое; (2) уменьшить подобранный коэффициент вдвое. Как изменяется характер движения робота? Удаётся ли ему пройти трассу? Какие участки наиболее проблемны?

Задание 9.8. Реализуйте алгоритм следования за рукой с использованием P-регулятора (см. задание 5.4 на с. 63). Настройте регулятор так, чтобы движение робота стало как можно более плавным.

Тем не менее, использование P-регулятора не позволяет решить задачу полностью: движение робота будет сильно зависеть от его конструкции, настроек регулятора и пр. Чтобы движение стало ещё стабильнее, нужно обратиться к более интеллектуальным алгоритмам. В первую очередь здесь следует назвать пропорционально-дифференциальный (PD) и пропорционально-интегрально-дифференциальный (PID) регуляторы. В настоящем пособии начального уровня указанные алгоритмы изучаться не будут. Интересующихся мы отсылаем к книге С. А. Филиппова [6], где подробно рассмотрены эти и другие интереснейшие задачи.

Пропорционально-интегрально-дифференциальный (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования.

Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегральным,пропорционально-дифференциальным, пропорциональным и т. п.

Содержание

Общие сведения

Пропорциональная составляющая

Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю.

Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать.

Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления, при наличии задержек в системе, могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.

Интегральная составляющая

Интегральная составляющая пропорциональна интегралу от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку.

Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечивать интегральная составляющая. Тем не менее, интегральная составляющая также может приводить к автоколебаниям.

Дифференциальная составляющая

Дифференциальная составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему.

Теория

Выходной сигнал регулятора u определяется тремя слагаемыми:Назначение ПИД-регулятора — в поддержании заданного значения x некоторой величины x с помощью изменения другой величины u. Значение x называетсязаданным значением (или уставкой, в технике), а разность e = (x − x) — невязкой (или ошибкой [регулирования], в технике), рассогласованием или отклонением величины от заданной.

,

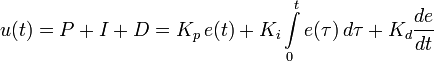
где К_p, К_i, К_d — коэффициенты усиления пропорциональной, интегральной и дифференциальной составляющих регулятора, соответственно.

Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегральная и дифференциальная составляющие:

В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму:

,

где — время дискретизации. Используя замену можно записать:

В программной реализации для оптимизации расчетов переходят к рекуррентной формуле:

Часто в качестве параметров ПИД-регулятора используются:

Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов.

Ссылки

Не правда ли программа, заданная в качестве задачки на понимание NXT-G вэтом посте, похожа на программы, поясняющие движение вдоль линии, в этом?

Разница между программами в том, что в одной используются сенсор расстояния, а в другой — сенсор овещенности. В остальном программы похожи: робот меняет направление поворота после того как значение на сенсоре измениться.

Если быть более точным, то в задаче робот поворачивает вправо, если расстояние на сенсоре меньше 14 см. и влево, если расстояние на сенсоре больше 16 см. Сложно представить, для чего может понадобиться такое движение, если сенсор смотрит вперед или назад. Но многое встает на свои места, если предположить, что сенсор установлен на одном из бортов робота и смотрит в сторону.

Если нарисовать схему такого движения, то становится видно, что по левому борту робота на протяжении всего движения, находится какое-то препятствие и робот пытается не подъезжать к нему слишком близко и не отъезжать слишком далеко. Если предположить, что препятствие это стена, то движение робота можно назвать движением вдоль стены. При некрутых заворотах стены, робот будет стараться держаться на определенном расстоянии, т.е. поворачивать вместе с заворотом стены.

Кстати, этот вариант ответа (движение вдоль стены) тоже был среди ответов, которые были присланы после публикации задачи.

Как и с предложенным алгоритмом движения вдоль линии, следует помнить, что данная реализация движения вдоль стены тоже является базовой для изучения. Т.е. при решениях реальных задач, алгоритм движения будет значительно сложнее, но принцип движения останется тот же.

Сейчас же хотелось бы обратить внимание на одну деталь, об которую довольно часто «спотыкаются» те, кто только начинает реализовывать дивжение вдоль стены.

В общем случае, движение робота параллельно стене и сенсор расстояния показывает вполне ожидаемые значение, на основе которых принимается решение в какую сторону поворачивать.

Но может возникнуть ситуация, когда робот в попытке вновь приблизиться к стене, значительно повернется к ней. Это приведет к тому, что сенсор начнет показывать очень большое расстояние — данные после отражения от стены не поступают в сенсор и он «думает», что препятствие еще слишком далеко.

В этом случае, робот будет стараться приблизиться к стене, увеличивая угол между сенсором и стеной, что только будет усугублять ситуацию.

Решение этой проблемы, традиционно, не одно. Оно может быть как программным, так и конструкторским. Например, можно не фиксировать датчик жестко, а поставить его на мотор.

Таким образом, после поворота робота, скажем, налево, сенсор расстояния поворачивается, стараясь быть направленным прямо на стену. А при повороте направо, мотор поворачивает сенсор в другую сторону:

Особенно такая схема удобна при сборке робота с управляющимим рулевым мотором, тогда сенсор можно крепить к тому же мотору, что управляет направляющими колесами. Причем лучше крепить не напрямую, а подобрать подходящее сочетание шестерней.

5.1.7. Движение вдоль стенки

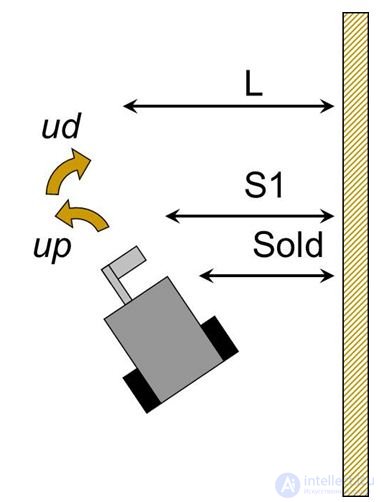
Решим такую задачу. Робот должен двигаться вдоль стенки на заданном расстоянии L. Предположим, что левое колесо робота управляется мотором В, правое — мотором С, а датчик расстояния, подключенный к порту 1, закреплен несколько впереди корпуса тележки (это важно!) и направлен на стенку справа по ходу движения.

Расстояние до стенки в настоящий момент времени, которое показывает датчик, обозначим .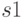

Моторы двигаются со средней скоростью 50, но при отклонении от заданного курса на них осуществляется управляющее воздействие up. Снова обозначим это следующим образом.

Осталось определить, чему будет равно управляющее воздействие. Это нетрудно:

Таким образом, при робот не меняет курса и едет прямо. В случае отклонения его курс корректируется. Здесь — это некоторый усиливающий коэффициент, определяющий воздействие регулятора на систему. Для робота NXT средних размеров коэффициент k может колебаться от 1 до 10 в зависимости от многих факторов. Предлагаем подобрать его самостоятельно.

В данном случае регулятор будет эффективно работать только при малых углах отклонения. Кроме того, движение практически всегда будет происходить по волнообразной траектории. Сделать регулирование более точным позволит введение новых принципов, учитывающих отклонение робота от курса.

5.1.8. Пропорционально-дифференциальный регулятор

В некоторых ситуациях П-регулятор может вывести систему из устойчивого состояния. Например, если робот направлен от стенки, но находится к ней ближе заданного расстояния, на моторы поступит команда еще сильнее повернуть от стенки, в результате чего с ней может быть утерян контакт (напоминаем, что датчик расстояния получает отраженный сигнал практически только от перпендикулярной поверхности).

Для защиты от подобных ситуаций добавим в регулятор дифференциальную составляющую, которая будет следить за направлением движения робота. Иными словами, вектор скорости будет влиять на управляющее воздействие. Известно, что скорость находится как , где — это изменение расстояния за промежуток времени . Определим дифференциальный регулятор через скорость отклонения робота от заданного положения:

где — текущее расстояние до стенки, — расстояние на предыдущем шаге.

Поскольку замеры производятся через равные промежутки времени, то можно принять за константу.

Таким образом, ПД-регулятор описывается формулой из двух слагаемых

Можно показать, что для устойчивого достижения цели коэффициент при дифференциальной составляющей должен превышать (см. ниже статью «Элементы теории автоматического управления в школе»).

Алгоритм движения вдоль стенки на ПД-регуляторе в целом будет выглядеть так:

Для объезда предметов потребуется ввести контроль показаний датчика расстояния: при резком изменении робот должен делать вывод о возможном повороте, который надо будет производить с другими коэффициентами.

Источник