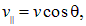движение протона в однородном магнитном поле
5.3. Движение заряда в однородном магнитном поле
Если начальная скорость заряженной частицы v перпендикулярна магнитному полю В, то в этом случае частица под действием силы Лоренца будет двигаться по окружности постоянного радиуса R (рис. 5.13)
Рис. 5.13. Движение отрицательно заряженной частицы в однородном магнитном поле
Сила Лоренца FL, направленная по радиусу к центру окружности, вызывает радиальное ускорение. По второму закону Ньютона имеем
следовательно, можем записать уравнение
из которого легко получить выражение для угловой скорости частицы
Если q, m и B — постоянные величины, то угловая скорость, а следовательно, и период
тоже являются постоянными величинами, не зависящими от энергии частицы. От скорости движения частицы зависит только радиус орбиты
Сила Лоренца создает только нормальное ускорение и, соответственно, направлена к центру окружности. Следовательно, направление вращения положительно заряженной частицы таково, что вращающийся в том же направлении винт будет двигаться против направления поля. Отрицательно заряженная частица вращается в противоположном направлении (см. рис. 5.14, 5.15).
Рис. 5.14. Движение положительно и отрицательно заряженных частиц в однородном магнитном поле.
Направление магнитного поля указано точками
Если начальная скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю. Частица будет продолжать двигаться в том же направлении прямолинейно и равномерно.
Наконец, в общем случае можно представить себе, что частица влетает в область однородного магнитного поля со скоростью v, составляющей угол q с направлением магнитного поля. Эту скорость можно разложить на компоненту две составляющих, одна из которых
направлена вдоль поля, а вторая
перпендикулярна полю. Соответственно, движение частицы является суммой двух движений: равномерного вдоль поля со скоростью 

Рис. 5.15. Движение заряженной частицы по спирали в однородном магнитном поле
Пример. В однородном магнитном поле с индукцией 2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом 10 см и шагом 60 см. Определить скорость и кинетическую энергию протона. Какую ускоряющую разность потенциалов U прошел протон перед тем, как влететь в магнитное поле?
Решение. Из уравнений (5.11) находим угол между скоростью протона и полем
Кинетическая энергия протона будет
Мы могли использовать нерелятивистскую формулу для энергии, так как скорость протона много меньше скорости света.
Если протон ускорялся электрическим полем, то при прохождении разности потенциалов U он приобрел энергию eU. Отсюда находим разность потенциалов
Джоуль — слишком большая энергия в мире элементарных частиц. Здесь используют внесистемную единицу — электронвольт (эВ).
Электрон-вольт (эВ) — это внесистемная единица энергии, численно равная энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов 1 В
Она удобна тем, что любая другая частица с зарядом по модулю равным заряду электрона, ускоренная разностью потенциалов в 3,66 МэВ, как в нашем примере, имеет кинетическую энергию 3,66 МэВ (мегаэлектронвольт).
Движение протона в однородном магнитном поле
Задание 17. Протоны в однородном магнитном поле между полюсами магнита движутся по окружностям радиусом R под действием силы Лоренца. После замены магнита по окружностям с тем же радиусом между полюсами стали двигаться α-частицы, обладающие такой же кинетической энергией, как и протоны. Как изменились индукция магнитного поля и скорость движения α-частиц по сравнению со скоростью протонов?
Альфа-частица имеет в своем составе два протона и два нейтрона, то ее масса по сравнению с протоном в 4 раза больше, а заряд в 2 раза больше заряда протона. Обозначим через q – заряд протона, а через m – его массу. Тогда кинетическую энергию для протона и α-частицы можно записать в виде:
По условию задания кинетические энергии равны, следовательно:
то есть, скорость α-частицы уменьшается в 2 раза.
Далее, на заряженную частицу со стороны магнитного поля действует сила Лоренца 


В соответствии со вторым законом Ньютона, силу Лоренца также можно записать как 


Учитывая, что α-частица имеет в своем составе два протона и два нейтрона, то ее масса по сравнению с протоном в 4 раза больше, а заряд в 2 раза больше заряда протона. Получаем:

Движение протона в однородном магнитном поле
Протон в однородном магнитном поле между полюсами магнита под действием силы Лоренца движется по окружности радиусом r. В этом же поле по окружности с таким же радиусом стала двигаться α-частица. Как изменились период обращения в магнитном поле и модуль импульса α-частицы по сравнению с протоном?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Период обращения | Модуль импульса |
При движении заряженной частицы в однородном магнитном поле по окружности параметры системы связаны между собой соотношениями
Значит, радиус обращения частицы равен А скорость частицы равна
Модуль импульса частицы будет равен
Период обращения равен Заряд альфа-частицы в два раза больше заряда протона, а её масса в четыре раза больше массы протона, следовательно, период обращения альфа-частицы в два раза больше, чем у протона, её импульс также в два раза больше, чем у протона.
Движение протона в однородном магнитном поле
Протоны в однородном магнитном поле между полюсами магнита движутся по окружностям радиусом R под действием силы Лоренца. После замены магнита по окружностям тем же радиусом между полюсами стали двигаться α-частицы, обладающие такой же кинетической энергией, как и протоны. Как изменились индукция магнитного поля и скорость движения α-частиц по сравнению со скоростью протонов?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
магнитного поля
При движении заряженной частицы в однородном магнитном поле по окружности параметры системы связаны между собой соотношениями
Индукция магнитного поля равна
Кинетическая энергия частицы выражается как Масса альфа-частицы в четыре раза больше массы протона, следовательно, при сохранении кинетической энергии, скорость альфа-частиц меньше скорости протонов в два раза. Заряд альфа-частицы в два раза больше заряда протона, тогда из формулы для индукции магнитного поля получаем, что индукция магнитного поля не изменилась.
Движение протона в однородном магнитном поле
Протон в однородном магнитном поле движется по окружности. Чтобы в этом поле двигалась по окружности с той же скоростью α-частица, радиус окружности, центростремительное ускорение и период обращения α-частицы по сравнению с протоном должны:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Радиус окружности | Центростремительное ускорение | Период обращения |
На заряженную частицу в магнитном поле действует сила Лоренца, которая сообщает ей центростремительное ускорение:
Поскольку массы и заряды протона и α-частицы связаны соотношениями
заключаем, что радиус окружности, по которой будет двигаться α-частица, приблизительно в 2 раза больше, чем у протона.
Следовательно, центростремительное ускорение будет меньше
Период обращения связан с радиусом траектории и скоростью соотношением
Поскольку радиус траектории у α-частицы больше, период обращения у нее больше.