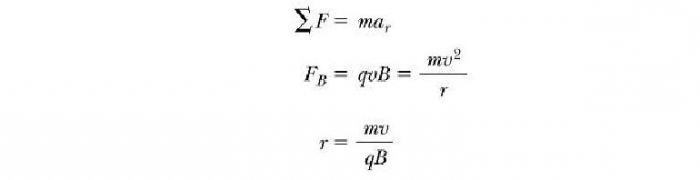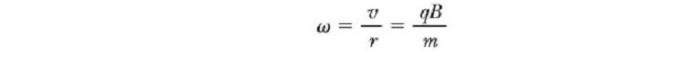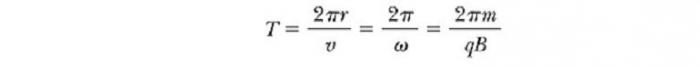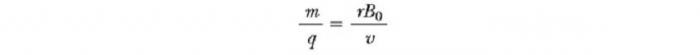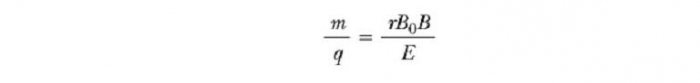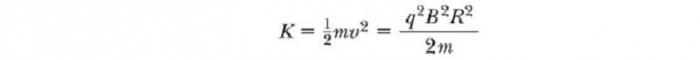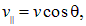движение по окружности в магнитном поле

Круговое движение в магнитном поле

При каких условиях заряженная частица в магнитном поле движется по кругу: направление магнитной силы и скорости движения, сила Лоренца, циклотронная частота.

Магнитная сила выступает перпендикулярной к скорости заряженной частички, которая будет двигаться по кругу.

Задача обучения

Основные пункты

Термины

Круговое перемещение заряженной частички в магнитном поле

Магнитные поля способны создавать круговые/спиральные пути для перемещения частиц. Ускорители удерживают протоны в этих маршрутах. Космические лучи следуют по спиралям при столкновении с магнитным полем небесных объектов. Изображение пузырьковой камеры ниже отображает заряженные частички, перемещающиеся по изогнутым путям.

Дорожки пузырьков создаются заряженными частицами с высокой энергией. Они перемещаются по нагретому жидкому водороду в пределах пузырьковой камеры. Присутствует мощное магнитное поле, создающее изогнутые траектории частиц. Радиус пути можно использовать для определения массы, заряда и энергии частичек

Стоит запомнить, что магнитная сила всегда выступает перпендикулярной по отношению к скорости, поэтому она не функционирует над заряженной частицей. В итоге, кинетическая энергия и скорость частицы остаются стабильными. Направление меняется, но не скорость. И это типичная ситуация для кругового движения.

Наиболее простой пример – перемещение заряженной частички перпендикулярно к однородному B-полюсу. Здесь магнитная сила вызывает центростремительную:

Частичка с отрицательным зарядом перемещается в плоскости, где магнитное поле выступает перпендикулярным. Магнитная сила также перпендикулярна скорости, поэтому последняя меняется по направлению, но остается стабильной по величине.

Отметив, что sinθ = 1, видим F = qvB.

Магнитная сила Лоренца обеспечивает центростремительную, поэтому составляющие равны:

Решение для

Здесь r – гирорадиус (радиус циклотрона), то есть это радиус кругового перемещения заряженной частички при наличии однородного магнитного поля. Если скорость не выступает перпендикулярной магнитному полю, то v перпендикулярно полю. Скоростная составляющая остается стабильной, потому что магнитная сила приравнивается к нулю.

Циклотронный резонанс – частичка в круговом движении при однородном магнитном поле. Термин взят из циклического ускорителя частиц (циклотрон). Циклотронная частота – количество циклов, отмечающее каждый круговой проход частички. Ее можно найти:

Французская модель циклотрона, созданная в Швейцарии (1937 год)

что превращается в

Циклотронная частота отображается в радианах в секунду за счет:

Источник

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Движение заряженных частиц в однородном магнитном поле

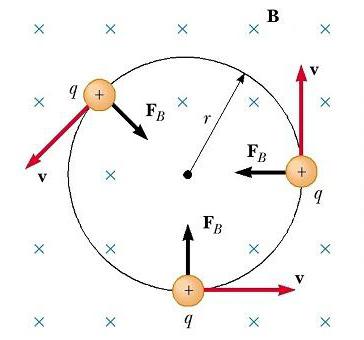
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

Движение частицы под углом к вектору магнитного поля

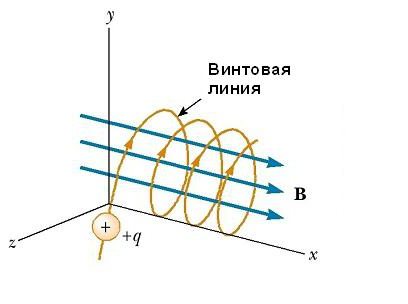
Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

Неоднородное магнитное поле: как в нем движутся частицы

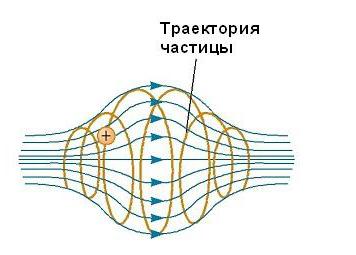
Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

Как Земля влияет на движение космических частиц

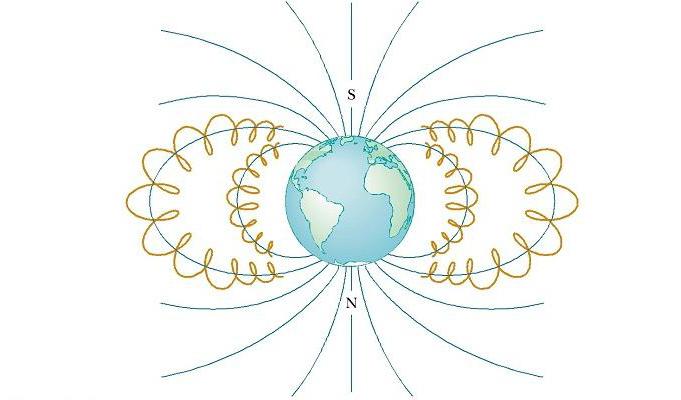
Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

Селектор скоростей

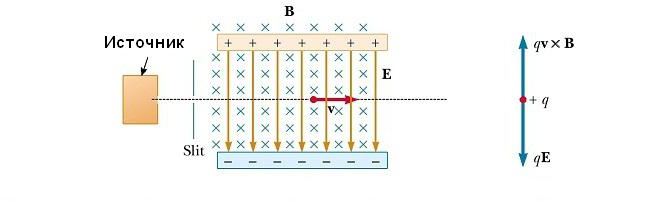
Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

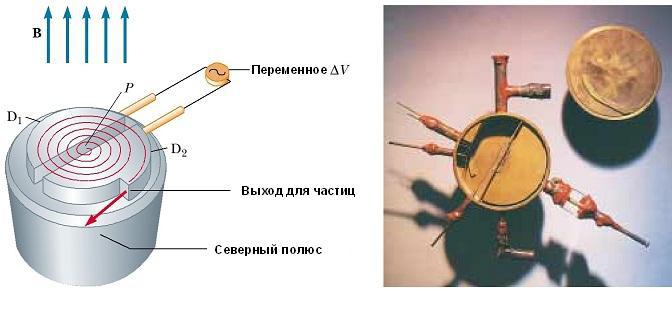
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Источник

5.3. Движение заряда в однородном магнитном поле

Если начальная скорость заряженной частицы v перпендикулярна магнитному полю В, то в этом случае частица под действием силы Лоренца будет двигаться по окружности постоянного радиуса R (рис. 5.13)

Рис. 5.13. Движение отрицательно заряженной частицы в однородном магнитном поле

Сила Лоренца F_L, направленная по радиусу к центру окружности, вызывает радиальное ускорение. По второму закону Ньютона имеем

следовательно, можем записать уравнение

из которого легко получить выражение для угловой скорости частицы

Если q, m и B — постоянные величины, то угловая скорость, а следовательно, и период

тоже являются постоянными величинами, не зависящими от энергии частицы. От скорости движения частицы зависит только радиус орбиты

Сила Лоренца создает только нормальное ускорение и, соответственно, направлена к центру окружности. Следовательно, направление вращения положительно заряженной частицы таково, что вращающийся в том же направлении винт будет двигаться против направления поля. Отрицательно заряженная частица вращается в противоположном направлении (см. рис. 5.14, 5.15).

Рис. 5.14. Движение положительно и отрицательно заряженных частиц в однородном магнитном поле.
Направление магнитного поля указано точками

Если начальная скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю. Частица будет продолжать двигаться в том же направлении прямолинейно и равномерно.

Наконец, в общем случае можно представить себе, что частица влетает в область однородного магнитного поля со скоростью v, составляющей угол q с направлением магнитного поля. Эту скорость можно разложить на компоненту две составляющих, одна из которых

направлена вдоль поля, а вторая

перпендикулярна полю. Соответственно, движение частицы является суммой двух движений: равномерного вдоль поля со скоростью и вращения по окружности с угловой скоростью . Траектория частицы, таким образом, является спиралью с радиусом R и шагом h (рис. 5.15):

Рис. 5.15. Движение заряженной частицы по спирали в однородном магнитном поле

Пример. В однородном магнитном поле с индукцией 2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом 10 см и шагом 60 см. Определить скорость и кинетическую энергию протона. Какую ускоряющую разность потенциалов U прошел протон перед тем, как влететь в магнитное поле?

Решение. Из уравнений (5.11) находим угол между скоростью протона и полем

Кинетическая энергия протона будет

Мы могли использовать нерелятивистскую формулу для энергии, так как скорость протона много меньше скорости света.

Если протон ускорялся электрическим полем, то при прохождении разности потенциалов U он приобрел энергию eU. Отсюда находим разность потенциалов

Джоуль — слишком большая энергия в мире элементарных частиц. Здесь используют внесистемную единицу — электронвольт (эВ).

Электрон-вольт (эВ) — это внесистемная единица энергии, численно равная энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов 1 В

Она удобна тем, что любая другая частица с зарядом по модулю равным заряду электрона, ускоренная разностью потенциалов в 3,66 МэВ, как в нашем примере, имеет кинетическую энергию 3,66 МэВ (мегаэлектронвольт).

Источник

Физика. 10 класс

§ 30. Сила Лоренца. Движение заряженных частиц в магнитном поле

Поскольку электрический ток представляет собой упорядоченное движение заряженных частиц, то это означает, что магнитное поле, действуя на проводник с током, действует тем самым на каждую из этих частиц. Таким образом, силу Ампера можно рассматривать как результат сложения сил, действующих на отдельные движущиеся заряженные частицы. Как можно определить силу, действующую со стороны магнитного поля на заряженную частицу, движущуюся в этом поле?

Сила Лоренца. Силу, которой магнитное поле действует на заряженную частицу, движущуюся в этом поле, называют силой Лоренца в честь выдающегося нидерландского физика Хендрика Антона Лоренца ( 1853–1928 ).

Поскольку – модуль средней скорости упорядоченного движения заряженной частицы в стационарном * электрическом поле внутри проводника, то формулу для определения модуля силы Лоренца можно записать в виде:

где α — угол между направлениями индукции магнитного поля и скорости упорядоченного движения заряженной частицы.

Из формулы (30.1) следует, что сила Лоренца максимальна в случае, когда заряженная частица движется перпендикулярно направлению индукции магнитного поля (α = 90°). Когда частица движется вдоль линии индукции поля (α = 0° или α = 180°), сила Лоренца на неё не действует. Сила Лоренца зависит от выбора инерциальной системы отсчёта, так как в разных системах отсчёта скорость движения заряженной частицы может отличаться.

Направление силы Лоренца, действующей на заряженную частицу, как и направление силы Ампера, определяют по правилу левой руки (рис. 168): если левую руку расположить так, чтобы составляющая индукции магнитного поля, перпендикулярная скорости движения частицы, входила в ладонь, а четыре пальца были направлены по движению положительно заряженной частицы (против движения отрицательно заряженной частицы), то отогнутый на 90° в плоскости ладони большой палец укажет направление действующей на частицу силы Лоренца.

Сила Лоренца перпендикулярна как направлению скорости движения частицы, так и направлению индукции магнитного поля.

* Электрическое поле, создаваемое и поддерживаемое источником тока в течение длительного промежутка времени и обеспечивающее постоянный электрический ток в проводнике, называют стационарным электрическим полем. ↑

Источник

Представление о магнитном поле

Мы все знаем, что такое постоянные магниты. Магниты – это металлические тела, притягивающиеся к другим магнитам и к некоторым металлам. То, что располагается вокруг магнита и взаимодействует с окружающими предметами (притягивает или отталкивает некоторые из них), называется магнитным полем.

Источником любого магнитного поля являются движущиеся заряженные частицы. А направленное движение заряженных частиц называется электрическим током. То есть, любое магнитное поле вызывается исключительно электрическим током.

За направление электрического тока принимают направление движения положительно заряженных частиц. Если же движутся отрицательные заряды, то направление тока считается обратным движению таких зарядов. Представьте себе, что по кольцевой трубе течет вода. Но мы будем считать, что некий «ток» при этом движется в противоположном направлении. Электрический ток обозначается буквой I.

В металлах ток образуется движением электронов – отрицательно заряженных частиц. На рисунке ниже, электроны движутся по проводнику справа налево. Но считается, что электрический ток направлен слева направо.

Это произошло потому, что когда начали изучение электрические явления, не было известно, какими именно носителями чаще всего переносится ток.

Если мы посмотрим на этот проводник с левой стороны, так, чтобы ток шел «от нас», то магнитное поле этого тока будет направлено вокруг него по часовой стрелке.

Если рядом с этим проводником расположить компас, то его стрелка развернется перпендикулярно проводнику, параллельно «силовым линиям магнитного поля» — параллельно черной кольцевой стрелке на рисунке.

Если мы возьмем шарик, имеющий положительный заряд (имеющий дефицит электронов) и бросим его вперед, то вокруг этого шарика появится точно такое же кольцевое магнитное поле, закручивающееся вокруг него по часовой стрелке.

Ведь здесь тоже имеет место направленное движение заряда. А направленное движение зарядов есть электрический ток. Если есть ток, вокруг него должно быть магнитное поле.

Движущийся заряд (или множество зарядов – в случае электрического тока в проводнике) создает вокруг себя «тоннель» из магнитного поля. Стенки этого «тоннеля» «плотнее» вблизи движущего заряда. Чем дальше от движущегося заряда, тем слабее напряженность («сила») создаваемого им магнитного поля. Тем слабее реагирует на это поле стрелка компаса.

Закономерность распределение напряженности магнитного поля вокруг его источника такая же, как закономерность распределения электрического поля вокруг заряженного тела – она обратно пропорциональна квадрату расстояния до источника поля.

Если положительно заряженный шарик перемещается по кругу, то кольца магнитных полей, образующихся вокруг него по мере его движения, суммируются, и мы получим магнитное поле, направленное перпендикулярно плоскости, в которой перемещается заряд:

Магнитный «тоннель» вокруг заряда оказывается свернутым в кольцо и напоминает по форме тор (бублик).

Такой же эффект получается, если свернуть в кольцо проводник с током. Проводник с током, свернутый в многовитковую катушку называется электромагнитом. Вокруг катушки складываются магнитные поля движущихся в ней заряженных частиц — электронов.

А если заряженный шарик вращать вокруг его оси, то у него появится магнитное поле, как у Земли, направленное вдоль оси вращения. В данном случае током, вызывающим появление магнитного поля, является круговое движение заряда вокруг оси шарика – круговой электрический ток.

Здесь, по сути, происходит то же самое, что и при движении шарика по кольцевой орбите. Только радиус этой орбиты уменьшен до радиуса самого шарика.

Все сказанное выше справедливо и для шарика заряженного отрицательно, но его магнитное поле будет направлено в противоположную сторону.

Данный эффект был обнаружен в опытах Роуланда и Эйхенвальда. Эти господа регистрировали магнитные поля вблизи вращающихся заряженных дисков: рядом с этими дисками начинала отклоняться стрелка компаса. Направления магнитных полей в зависимости от знака заряда дисков и направления их вращения, показаны на рисунке:

При вращении незаряженного диска, магнитные поля не обнаруживались. Не было магнитных полей и вблизи неподвижных заряженных дисков.

Модель магнитного поля движущегося заряда

Чтобы запомнить направление магнитного поля движущегося положительного заряда, мы представим себя на его месте. Поднимем правую руку вверх, затем укажем ею направо, затем опустим ее вниз, затем укажем влево и вернем руку в исходное положение – вверх. Затем повторим это движение. Наша рука описывает круги по часовой стрелке. Теперь начнем движение вперед, продолжая вращать рукой. Движение нашего тела – аналог движения положительного заряда, а вращение руки по часовой стрелке – аналог магнитного поля заряда.

Теперь представьте себе, что вокруг нас находится тонкая и прочная эластичная паутина, похожая на струны пространства, которые мы рисовали, создавая модель электрического поля.

Когда мы движемся сквозь эту трехмерную «паутину», из-за вращения руки, она, деформируясь, смещается по часовой стрелке, образуя подобие спирали, словно бы наматываясь в катушку вокруг заряда.

Сзади, за нами, «паутина» восстанавливает свою правильную структуру. Примерно так можно представлять себе магнитное поле положительного заряда, движущегося прямо.

А теперь попробуйте двигаться не прямо вперед, а по кругу, например, поворачивая при ходьбе налево, при этом вращая рукой по часовой стрелке. Представьте себе, что вы движетесь через нечто, напоминающее желе. Из-за вращения вашей руки, внутри круга, по которому вы движетесь, «желе» будет смещаться вверх, образуя горб над центром круга. А под центром круга, образуется впадина из-за того, что часть желе сместилось вверх. Так можно представлять себе формирование северного (горб сверху) и южного (впадина снизу) полюсов при движении заряда по кольцу или его вращения.

Если при ходьбе вы будете поворачивать направо, то «горб» (северный полюс) сформируется снизу.

Аналогично можно сформировать представление о магнитном поле движущегося отрицательного заряда. Только вращать рукой нужно в противоположную сторону – против часовой стрелки. Соответственно, магнитное поле будет направлено в противоположную сторону. Просто каждый раз следите за тем, в какой сторону ваша рука выталкивает «желе».

Такая модель наглядно демонстрирует то, почему северный полюс одного магнита притягивается к южному полюсу другого магнита: «горб» одного из магнитов втягивается во «впадину» второго магнита.

И еще эта модель показывает, почему не существуют отдельных северных и южных полюсов магнитов, как бы мы их не разрезали – магнитное поле представляет собой вихревую (замкнутую) «деформацию пространства» вокруг траектории движущегося заряда.

У электрона было обнаружено магнитное поле, такое, какое у него должно быть в том случае, если бы он был шариком, вращающимся вокруг своей оси. Это магнитное поле назвали спином (от английского to spin — вращаться).

Кроме того, у электрона существует еще и орбитальный магнитный момент. Ведь электрон не только «вращается», но движется по орбите вокруг ядра атома. А движение заряженного тела порождает магнитное поле. Так как электрон заряжен отрицательно, магнитное поле, вызванное его движением по орбите, будет выглядеть так:

Если направление магнитного поля, вызванного движением электрона по орбите, совпадает с направлением магнитного поля самого электрона (его спином), эти поля складываются и усиливаются. Если же эти магнитные поля направлены в разные стороны, они вычитаются и ослабляют друг друга.

Кроме того, могут суммироваться или вычитаться друг из друга магнитные поля других электронов атома. Этим объясняется наличие или отсутствие магнетизма (реакции на внешнее магнитное поле или наличие собственного магнитного поля) некоторых веществ.

Эта статья — отрывок из книги об азах химии. Сама книга здесь:
sites.google.com/site/kontrudar13/himia

UPD: Материал предназначен, в первую очередь, для школьников средних классов. Возможно, Хабр не место для подобных вещей, Но где место? Нет его.

Источник