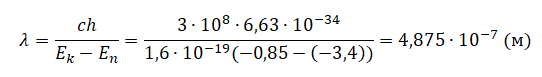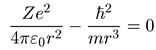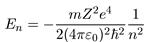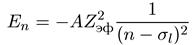движение электрона в кулоновском поле
Постулаты Бора
теория по физике 🧲 квантовая физика
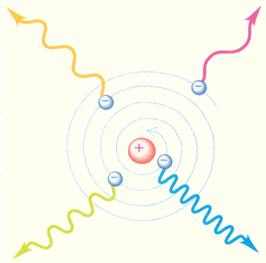
Следующий шаг в развитии представлений об устройстве атома в 1913 году сделал выдающийся датский физик Н. Бор. Проанализировав всю совокупность опытных фактов, Бор пришел к выводу, что при описании поведения атомных систем следует отказаться от многих представлений классической физики. Он сформулировал постулаты, которым должна удовлетворять новая теория о строении атомов.
Квантовые постулаты Бора – предположения (утверждения), сделанные Н. Бором для того, чтобы модель строения атома Резерфорда соответствовала реальному поведению атомов водорода.
Первый постулат Бора
Первый постулат Бора также носит название постулата стационарных состояний:
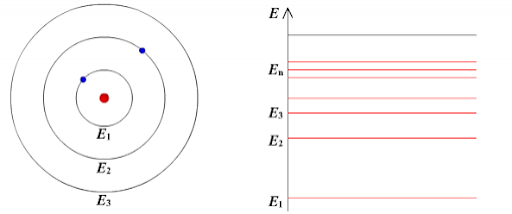
Атомная система может находиться только в стационарных, или квантовых, состояниях, каждому из которых соответствует определенная энергия En. В стационарном состоянии атом не излучает электромагнитные волны.
Этот постулат находится в явном противоречии с классической механикой, согласно которой энергия движущегося электрона может быть любой. Он находится в противоречии и с электродинамикой, так как допускает возможность ускоренного движения электронов без излучения электромагнитных волн.
Второй постулат Бора
Второй постулат Бора также носит название правила частот:
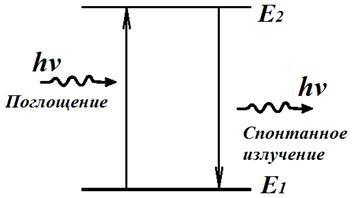
Излучение света происходит при переходе атома из стационарного состояния с большей энергией Ek в стационарное состояние с меньшей энергией En. Энергия излученного фотона равна разности энергий стационарных состояний.
Разность энергий стационарных состояний можно вычислить по формуле:
Внимание! В квантовой физике энергию принято измерять не в Джоулях, а в электрон-вольтах, обозначаемых «эВ». 1 эВ равен энергии, приобретаемой электроном при прохождении разницы потенциалов 1 В. 1 эВ = 1,6∙10 –19 Дж.
Отсюда можно выразить частоту излучения:
Частоту найдем по формуле:
Следовательно, длина волны равна:
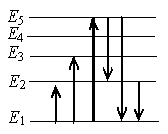
а) с уровня 1 на уровень 5
б) с уровня 5 на уровень 2
в) с уровня 5 на уровень 1
г) с уровня 2 на уровень 1
Алгоритм решения
Решение
Излучение света происходит при переходе атома из стационарного состояния с большей энергией Ek в стационарное состояние с меньшей энергией En. Энергия излученного фотона равна разности энергий стационарных состояний.
Причем чем на более высоком уровне находится электрон, тем с более высокой энергией фотон он испускает при переходе на 1 уровень. Поэтому на рисунке нам подходит переход с уровня 5 на уровень 1.
pазбирался: Алиса Никитина | обсудить разбор | оценить
В сосуде находится разреженный атомарный водород. Атом водорода в основном состоянии (Е1 = – 13,6 эВ) поглощает фотон частотой 3,7⋅10 15 Гц. С какой скоростью υ движется вдали от ядра электрон, вылетевший из атома в результате ионизации? Энергией теплового движения атомов водорода пренебречь.
Движение электрона в кулоновском поле
Электрон. Образование и строение электрона. Магнитный монополь электрона.
Часть 4. Строение электрона.
4.5. Определить внутреннее строение электрона весьма затруднительно по многим причинам, тем не менее, представляет значительный интерес хотя бы в первом приближении рассмотреть влияние двух компонент (электрической и магнитной) на внутреннее строение электрона. См. рис. 7.

Рис.7. Внутреннее строение электрона, варианты:
Вариант №1. Каждая пара лепестков отрицательного полукванта образует «микроэлектроны», которые затем формируют электрон. При этом количество «микроэлектронов» должно быть кратным трём.
Вариант №4. Другие варианты.
По-видимому, может быть рассмотрен вариант когда электрические (-) и магнитные поля (N) могут существовать внутри электрона не только в виде компактных монополей, но и в виде однородной субстанции, то есть образуют практически бесструктурную? кристаллическую? гомогенную? частицу. Однако это весьма сомнительно.
4.6. Каждый из предложенных на рассмотрение вариантов имеет свои достоинства и недостатки, например:
а) Варианты №1. Электроны такой конструкции дают возможность спокойно образовывать дробные частицы с массой и зарядом кратным 1/3, но в то же время делают затруднительным объяснение собственного магнитного поля электрона.
4.7. При рассмотрении указанных (или вновь предложенных) вариантов в обязательном порядке необходимо учитывать реально существующие свойства и характеристики электрона, а также учитывать ряд обязательных требований, например:
— наличие электрического поля (заряда);
— наличие магнитного поля;
— эквивалентность некоторых параметров, например: масса электрона эквивалентна его заряду и наоборот;
— возможность образовывать дробные частицы массой и зарядом кратным 1/3;
— наличие набора квантовых чисел, спина и др.
4.8. Электрон появился как двухкомпонентная частица, у которой одна половина (1/2) является уплотнённым электрическим полем-минус (электрическим монополем-минус), а вторая половина (1/2) является уплотнённым магнитным полем (магнитным монополем-N). Однако при этом следует иметь в виду, что:
— электрические и магнитные поля при определённых условиях могут порождать друг друга (превращаться друг в друга);
— электрон не может быть однокомпонентной частицей и состоять на 100% из поля-минус, поскольку однозарядное поле-минус будет распадаться из-за сил отталкивания. Именно поэтому внутри электрона необходимо наличие магнитной компоненты.
4.9. К сожалению, провести полный анализ всех достоинств и недостатков предложенных вариантов и выбрать единственно правильный вариант внутреннего строения электрона в данной работе не представляется возможным.
Часть 5. «Волновые свойства электрона».
5.1. «К концу 1924г. точка зрения, согласно которой электромагнитное излучение ведет себя отчасти подобно волнам, а отчасти подобно частицам, стала общепринятой. И именно в это время француза Луи де Бройля, который в то время был аспирантом, осенила гениальная мысль: почему то же самое не может быть для вещества? Луи де Бройль проделал по отношению к частицам работу, обратную той, которую Эйнштейн провел для волн света. Эйнштейн связал электромагнитные волны с частицами света; де Бройль связал движение частиц с распространением волн, которые он назвал волнами материи. Гипотеза де Бройля основывалась на сходстве уравнений, описывающих поведение лучей света и частиц вещества, и носила исключительно теоретический характер. Для ее подтверждения или опровержения требовались экспериментальные факты».(с)
5.2. «В 1927 году американские физики К.Дэвиссон и К.Джермер обнаружили, что при «отражении» электронов от поверхности кристалла никеля при определённых углах отражения возникают максимумы. Аналогичные данные (возникновение максимумов) уже имелись по наблюдению дифракции рентгеновских волн лучей на кристаллических структурах. Поэтому появление этих максимумов у отражённых пучков электронов не могло быть объяснено никаким другим путём, кроме как на основе представлений о волнах и их дифракции. Таким образом, волновые свойства частиц — электронов (и гипотеза де Бройля) были доказаны экспериментом».(с)
5.3. Однако рассмотрение изложенного в данной работе процесса появления корпускулярных свойств у фотона (см. рис.5.) позволяет сделать вполне однозначные выводы:
в) поэтому рентгеновский фотон при взаимодействии с препятствием уже не отражается от препятствия как волна, а начинает отскакивать от него как частица.
а) уже в диапазоне мягкого рентгена электромагнитные поля фотонов настолько уплотнились, что обнаружить у них волновые свойства весьма затруднительно. Цитата: «Чем меньше длина волны фотона, тем труднее обнаружить у него свойства волны и тем сильнее у него проявляются свойства частицы».
б) в жестком рентгеновском и гамма-диапазоне фотоны ведут себя как стопроцентные частицы, и обнаружить у них волновые свойства уже практически невозможно. То есть: рентгеновский и гамма-фотон полностью теряет свойства волны и превращается в стопроцентную частицу. Цитата: «Энергия квантов в рентгеновском и гамма-диапазоне настолько велика, что излучение ведёт себя почти стопроцентно как поток частиц» (с).
в) поэтому в опытах по рассеиванию рентгеновского фотона от поверхности кристалла наблюдалась уже не волна, а обыкновенная частица, которая отскакивала от поверхности кристалла и повторяла строение кристаллической решётки.
5.5. До опытов К.Дэвиссона и К.Джермера уже имелись экспериментальные данные по наблюдению дифракции рентгеновских волн лучей на кристаллических структурах. Поэтому получив схожие результаты в опытах при рассеивании электронов на кристалле никеля, они автоматически приписали электрону волновые свойства. Однако электрон это «твердая» частица, которая имеет реальную массу покоя, габариты и пр. Не электрон-частица ведет себя как фотон-волна, а рентгеновский фотон имеет (и проявляет) все свойства частицы. Не электрон отражается от препятствия как фотон, а рентгеновский фотон отражается от препятствия как частица.
5.6. Поэтому: никаких «волновых свойств» у электрона (и других частиц) не было, нет и быть не может. И не существует никаких предпосылок и тем более возможностей для изменения данной ситуации.
6.1.Электрон и позитрон являются первыми и основообразующими частицами, наличие которых определило появление кварков, протонов, водорода и всех остальных элементов таблицы Менделеева.
6.2. Исторически, одну частицу назвали электроном и присвоили ей знак минус (материя), а другую назвали позитроном и присвоили ей знак плюс (антиматерия). «Электрический заряд электрона условились считать отрицательным в соответствии с более ранним соглашением называть отрицательным заряд наэлектризованного янтаря» (с).
6.3. Электрон может появиться (появиться = родится) только в паре с позитроном (электрон позитронная пара). Появление в Природе хотя бы одного «непарного» (одиночного) электрона или позитрона является нарушением закона сохранения заряда, общей электронейтральности материи и технически невозможно.
6.7. Магнитные монополи существуют, но не в свободном виде, а только как составные части электрона и позитрона. При этом магнитный монополь-(N) является неотъемлемой частью электрона, а магнитный монополь-(S) является неотъемлемой частью позитрона. Наличие магнитной составляющей «внутри» электрона обязательно, поскольку только магнитный монополь-(N) может образовать с однозарядным электрическим монополем-минус прочнейшую (и невиданную по силе) связь.
6.9. Электрон вечен и он не может «исчезнуть» до тех пор, пока не встретится с другой частицей, имеющей равные по величине, но противоположные по знаку электрический и магнитный заряды (позитрон).
6.10. Поскольку из электромагнитных волн могут появиться только две эталонные (калиброванные) частицы: электрон и позитрон, то на их основе могут появиться только эталонные кварки, протоны и нейтроны. Поэтому вся видимая (барионная) материя нашей и всех других вселенных состоит из одинаковых химических элементов (таблица Менделеева) и везде действуют единые физические константы и фундаментальные законы, аналогичные «нашим» законам. Появление в любой точке бесконечного пространства «других» элементарных частиц и «других» химических элементов – исключается.
6.11. Вся видимая материя нашей Вселенной образовалась из фотонов (предположительно СВЧ-диапазона) по единственно возможной схеме: фотон → электрон-позитронная пара → дробные частицы → кварки, глюон → протон (водород). Поэтому вся «твёрдая» материя нашей Вселенной (включая Homo sapiens’ов) является уплотнёнными электрическими и магнитными полями фотонов. Других «материй» для её образования в Космосе не было, нет и быть не может.
Заряженная частица в кулоновском поле
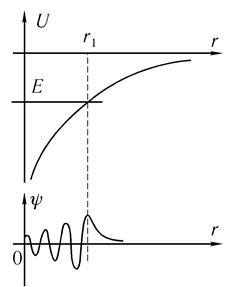
Перейдем к задаче о движении заряженной частицы в кулоновском потенциале (рис. 5.5). Для нас это одна из самых интересных задач, поскольку она описывает состояния электрона в атоме.
Мы уже не раз обсуждали вопрос о том, как найти основное состояние квантовой системы — надо минимизировать, с учетом соотношения неопределенностей, полную энергию. Для электрона, находящегося в кулоновском поле ядра с зарядом Ze, полная энергия определяется выражением
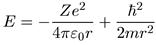
Дифференцирование этого выражения по r приводит к следующему условию для минимального значения энергии:

Мы получили значение боровского радиуса для элек-
трона в поле ядра с зарядом Ze. Такой атом называется водородоподобным. Энергию основного состояния можно найти, подставляя

Аналогичным образом могут быть найдены возбужденные состояния. Волновые функции высших квантовых состояний, согласно осцилляционной теореме, имеют п узлов. Поэтому характерная длина волны А такого состояния будет равна 2тгг/п, что приводит к увеличению кинетической энергии этих состояний. Действительно, электрон локализован в пространстве в области размером порядка А, и поэтому его импульс, согласно соотношению неопределенностей, может быть оценен как
а кинетическая энергия
n 2 ћ 2 /(2mr 2 ). (5.42)
Если провести минимизацию полной энергии, как это делалось выше, то мы
получим для состояния с квантовым числом п
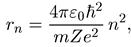
что соответствует радиусу его боровской орбиты, а для энергии этого состояния:
Фактически, дискретные значения энергии электрона в атоме следуют из
Мы предположили, что радиус орбиты r имеет фиксированное значение.
Согласно квантовой механике радиусы орбит «разбросаны» в окрестности
классически устойчивой орбиты. В качестве оценки взято значение r, которое соответствует минимуму энергии Е(r). В действительности электрон может находиться с разной вероятностью на любом расстоянии от ядра.
Наше упрощение состоит в предположении, что это определенное, равное r расстояние находится из условия минимальности полной энергии. Поэтому нельзя доверять числовому множителю впереди полученной формулы, хотя он случайно и оказался правильным. Однако всему остальному, а главное, зависимости от квантового числа n, доверять можно.
Отметим также, что в формулу (5.44) для уровней энергии атома водорода, строго говоря, входит не масса электрона, а приведенная масса системы протон-электрон. Поэтому спектры энергии, например, обычного водорода и его тяжелого изотопа — дейтерия — несколько отличаются друг от друга (так называемый изотопический сдвиг). Существование данного эффекта экспериментально наблюдается не только для водорода, что вполне понятно, поскольку полученное решение справедливо для любой «водородоподобной» системы — системы из двух частиц с противоположными зарядами,
274 mе). В этих и других такого рода доподобных системах эффект изотопического сдвига сказывается особенно заметно.
где σl — поправка на неточечность, зависящая от орбитального движения
электрона (от типа симметрии его движения), a Zэф — эффективный заряд ядра, учитывающий экранирующее действие электронов замкнутой оболочки.
Одно замечание: при решении мы считали, что ψ-функция — это функция
только расстояния частицы от кулоновского центра, а не угловых переменных, т. е. искали сферически симметричные решения. Позже мы выясним, чему соответствуют решения, не обладающие сферической симметрией. Сейчас лишь отметим, что решение полной задачи не приводит к появлению новых уровней энергии.
Электрон в центральном поле
Решения уравнения Шрёдингера для электрона в центральном поле играют определяющую роль для рассмотрения строения и свойств атома водорода, водородоподобных ионов, классификации электронных состояний и нахождения приближенных решений для атомов и ионов любых химических элементов и молекулярных систем.
Уравнение Шрёдингера для электрона, движущегося на расстоянии г в центральном поле с зарядом Z, имеет вид
Для решения задачи переходят к сферическим координатам (г, 0, ср), что позволяет разделить переменные. В этих координатах оператор Лапласа А = V 2 имеет вид
В таком случае собственные функции уравнения Шрёдингера можно выразить как произведение трех функций: /?, 0 и Ф, каждая из которых зависит только от одной сферической координаты
После подстановки (3.14) и (3.15) в (3.13) уравнение Шрёдингера принимает вид
Разделив выражение (3.16) на sin 2 0, вновь удается разделить переменные в левой и правой частях уравнения:
Обозначив постоянную величину буквой с, получаем два уравнения:
Уравнение Шрёдингера для радиальной части волновой функции (3.18) электрона принимает вид
Его собственные значения, являющиеся энергией электрона в центральном кулоновском поле, равны
где главное квантовое число «=1,2,оо.
ственной радиальной функции имеет вид
где L 2 J*I (q) — присоединенный полином Лягера, который связан с полиномом Лягера /фТ) дифференциальным соотношением
Nш — коэффициент нормировки.
Так как г — сферическая координата, то для вычисления коэффициента нормировки нужно брать интеграл вида
Здесь опущен знак модуля, потому что Rnl — вещественная функция. Интегрирование последнего выражения позволяет получить значение нормировочного множителя собственной радиальной функции:
Они являются ортогональными функциями при различных значениях квантового числа / и при одинаковых значениях т.
Полные собственные функции для электрона в кулоновском поле имеют вид
Согласно формуле (3.20) собственные значения Еп зависят только от главного квантового числа п, тогда как собственные функции (3.21) нумеруются тремя квантовыми числами пу /, т и зависят от значений всех трех квантовых чисел. Это означает, что электрон в центральном поле точечного заряда ядра находится в вырожденном по энергии состоянии.
Электрон в центральном поле
Для электрона в кулоновском поле ядра с зарядом Z в выражение для гамильтониана Дирака свободного электрона (7.8) необходимо добавить оператор потенциальной энергии
Рис. 7.1. Спектр собственных значений гамильтониана Дирака при кулоновском потенциале.
U = —. Тогда получаем г
Данное уравнение при кулоновском потенциале U решается точно, давая решения для электронных и позитронных состояний. Спектр собственных значений его качественно представлен на рис. 7.1 и содержит непрерывные и дискретные решения для электрона и позитрона.
В отличие от уравнения Шрё- дингера уравнение на собственные значения с гамильтонианом Дирака не приводит к раздельным законам сохранения спинового и орбитального моментов.
Решение уравнения Дирака приводит к следующему выражению для энергии электрона:
где но сравнению с величинами в нсрелятивистском выражении (3.20) появились энергия покоя m0c 2 = 1 137 2 = 18 769 а.е., внутреннее квантовое число j и постоянная тонкой структуры 1 1
Внутреннее квантовое число j является собственным значением оператора полного момента и принимает значения j = /±^. Таким образом, каждому значению орбитального квантового числа / соответствуют два значения j, поэтому энергетические уровни оказываются двукратно расщепленными. Только для 5-уровней вырождение отсутствует, гак как при / = 0 имеется только одно 1
Исходя из приведенных значений квантовых чисел схематично релятивистская энергетическая диаграмма электрона атома водорода имеет вид, представленный на рис. 7.2.
Условное обозначение энергетического уровня включает значение главного квантового числа, буквенное обозначение орбитального квантового числа и справа внизу подстрочным символом значение внутреннего квантового числа — nl.
Рис. 7.2. Релятивистская энергетическая диаграмма атома водорода
Энергетическая диаграмма (см. рис. 7.2) и формула (7.12) позволили описать так называемую тонкую структуру спектральных линий водорода, заключающуюся в том, что имеет место расщепление энергетических уровней, наблюдаемое экспериментально, но не предсказываемое решением уравнения Шрёдингера.
энергия, но и другие физические свойства изменяются при учете релятивизма пропорционально заряду ядра в четвертой степени.
Волновые функции электрона в атоме водорода по теории Дирака используют в виде, подобном нерелятивистским функциям:
Выразим каждую четырехкомпонентную волновую функцию Т в виде пары двухкомпонентных спиноров Ф и 0:
При этом каждый двухкомпонентный спинор может быть представлен в виде произведения радиальной функции на двухкомпонентную собственную функцию оператора j, зависящую от спиновой и угловых координат:
Собственные функции могут быть выражены в виде сумм прямых произведений уже известных нам собственных функций операторов момента количества движения, проекции спина и соответствующих так называемых коэффициентов Клейна — Гордона

В представленных выражениях У> 2 — сферические гармоники, а функции
В итоге получаются следующие формы четырехкомпонентных волновых функций: