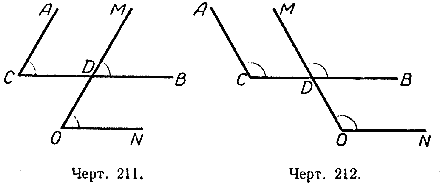Что значит углы с взаимно перпендикулярными сторонами

Углы с соответственно перпендикулярными сторонами равны между собой, если они оба острые или оба тупые.

21.04.2020

Углы со взаимно перпендикулярными и взаимно параллельными сторонами.

Углы с соответственно параллельными сторонами.

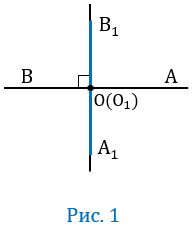
Возьмём на плоскости две точки С и О и из этих точек проведём две пары лучей
СА || ОМ и СВ || ОN так, чтобы углы АСВ и МОN были или оба острые (рис. 1), или оба тупые (рис. 2).

Рис. 1

Рис. 2

Углы АСВ и МОN— углы с соответственно параллельными cторонами. Докажем, что эти углы равны между собой.

Пусть СВ пересекает ОМ в точке D. , как соответственные углы при параллельных АС и МО и секущей СВ.

, как соответственные углы при параллельных СВ и ОN и секущей МО, но тогда и .

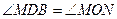
Следовательно, углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые.

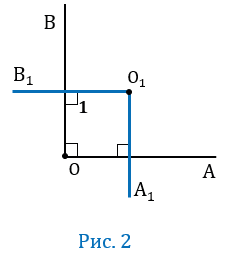
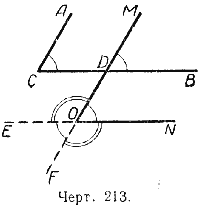
Рис.3

Построим два острых угла АСВ и МОN с соответственно параллельными сторонами (рис. 3): СА || МО и СВ || ОN, и продолжим за вершину О стороны угла МОN. При вершине О образовались два тупых угла ЕОМ и FОN (так как смежный с ними угол МОN по построению острый). Каждый из них в сумме с углом МОN составляет 2d, а так как , то и .

Углы с соответственно перпендикулярными сторонами.

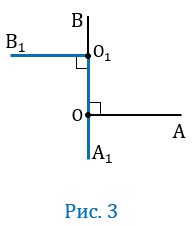
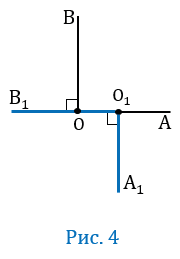
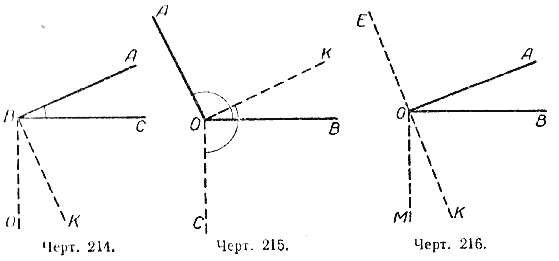
Рис. 4	Построим произвольный острый угол АВС. Проведём через вершину угла лучи, перпендикулярные к его сторонам, так, чтобы они образовали острый угол. BO_|_ ВС и ВК _|_ АВ (рис. 4). Мы получим новый угол OBK. Стороны углов AВС и ОВК взаимно перпендикулярны. / АВС = d — / СВК; / ОВК = d — / СВК. Отсюда следует, что / АBС = / ОВК.
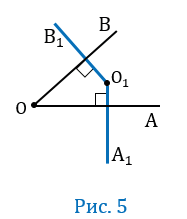
Построим произвольный тупой угол АОВ и через его вершину проведём лучи, перпендикулярные к его сторонам, так, чтобы они образовали тупой угол. ОК_|_ОА и ОС_|_ОВ (рис. 5), угол КОС — тупой. Стороны углов АОВ и КОС взаимно перпендикулярны, поэтому / АОВ = d + / КОВ; / КОС = d + / КОВ. Отсюда следует, что / АОВ = / КОС.	Рис. 5

Углы с соответственно перпендикулярными сторонами равны между собой, если они оба острые или оба тупые.

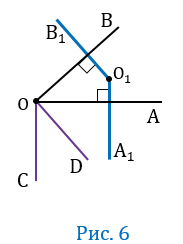
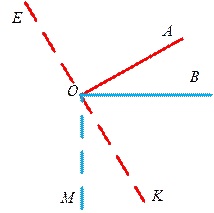Рис. 6

Построим произвольный острый угол АОВ и проведём через его вершину перпендикуляры к его сторонам так, чтобы они образовали острый угол (рис. 6). Получим: / КОМ = / АОВ. Продолжим сторону ОК за вершину О. Стороны угла ЕОМ перпендикулярны сторонам угла АОВ. При этом / ЕОМ — тупой, так как смежный с ним / МОК — острый. / КОМ + / ЕОМ = 2d (как углы смежные). Но / КОМ по ранее доказанному равен / АОВ. Следовательно, и / АОВ + / ЕОМ = 2d.

Углы с соответственно перпендикулярными сторонами в сумме составляют 2d, если один из них острый, а другой тупой.

Мы рассматривали углы, составленные взаимно перпендикулярными сторонами, когда они имели общую вершину. Выведенные нами свойства будут справедливы и в том случае, когда углы не будут иметь общей вершины.

Источник

Теорема об углах с соответственно перпендикулярными сторонами

Теорема

Дано: АОВ, А₁О₁В₁, ОАО₁А₁, ОВО₁В₁.

Доказать: АОВ = А₁О₁В₁ или АОВ + А₁О₁В₁ = 180 0 .

Доказательство:

1 случай

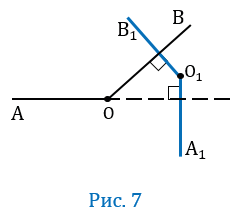
Пусть угол АОВ — развернутый (Рис. 1).

Угол АОВ — развернутый, значит лучи ОА и ОВ будут лежать на одной прямой, при этом по условию ОАО₁А₁, ОВО₁В₁, значит, лучи О₁А₁ и О₁В₁ также будут лежать на одной прямой, следовательно, А₁О₁В₁ — будет развернутым, тогда АОВ = А₁О₁В₁.

2 случай

Пусть угол АОВ — прямой, т.е. равен 90 0 (Рис.2).

3 случай

Пусть ОО₁А₁ (Рис.3).

По условию ОО₁А₁, тогда лучи ОВ и О₁А₁ будут лежать на одной прямой А₁В. По условию ОАО₁А₁, ОВО₁В₁, значит, ОА и О₁В₁ будут перпендикулярны одной прямой А₁В, следовательно, ОАО₁В₁. Итак, ОАО₁В₁, А₁В — секущая относительно прямых ОА и О₁В₁, тогда по теореме о накрест лежащих углах АОВ = А₁О₁В₁, причем, учитывая то, что ОАО₁А₁, ОВО₁В₁ эти углы будут прямые, т.е. АОВ = А₁О₁В₁ = 90 0 , тогда АОВ + А₁О₁В₁ = 90 0 + 90 0 = 180 0 .

4 случай

Пусть ОО₁В₁ (Рис.4).

По условию ОО₁В₁, тогда лучи ОА и О₁В₁ будут лежать на одной прямой В₁А. По условию ОАО₁А₁, ОВО₁В₁, значит ОВ и О₁А₁ будут перпендикулярны одной прямой В₁А, следовательно, ОВО₁А₁. Итак, ОВО₁А₁, В₁А — секущая относительно прямых ОВ и О₁А₁, тогда по теореме о накрест лежащих углах АОВ = А₁О₁В₁, причем, учитывая то, что ОАО₁А₁, ОВО₁В₁ эти углы будут прямые, т.е. АОВ = А₁О₁В₁ = 90 0 , тогда АОВ + А₁О₁В₁ = 90 0 + 90 0 = 180 0 .

5 случай

Пусть угол АОВ — острый, т.е. меньше 90 0 , при этом ОО₁А₁, ОО₁В₁ (Рис.5).

Проведем луч ОС так, чтобы прямые ОА и ОС были взаимно перпендикулярными (т.е. ОАОС), а точки В и С лежали по разные стороны от прямой ОА. Далее проведем луч ОD так, чтобы прямые ОВ и ОD были взаимно перпендикулярными (т.е. ОВОD), а точки С и D лежали по одну сторону от прямой ОА (Рис.6).

6 случай

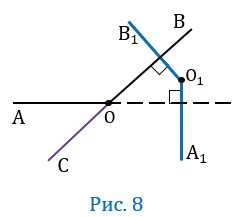
Пусть угол АОВ — тупой, т.е. меньше 180 0 , но больше 90 0 , при этом ОО₁А₁, ОО₁В₁ (Рис.7).

Проведем луч ОС так, чтобы угол АОС был смежным с углом АОВ (Рис.8).

Поделись с друзьями в социальных сетях:

Источник

Что значит углы с взаимно перпендикулярными сторонами

ГЛАВА III.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ

§ 40. УГЛЫ С СООТВЕТСТВЕННО ПАРАЛЛЕЛЬНЫМИ
И ПЕРПЕНДИКУЛЯРНЫМИ СТОРОНАМИ.

1. Углы с соответственно параллельными сторонами.

Возьмём на плоскости две точки С и О и из этих точек проведём две пары лучей
СА || ОМ и СВ || ОN так, чтобы углы АСВ и МОN были или оба острые (черт. 211), или оба тупые (черт. 212).

Углы АСВ и МОN— углы с соответственно параллельными cтронами. Докажем, что эти углы равны между собой.

Пусть СВ пересекает ОМ в точке D. / АСВ = / МDВ, как соответственные углы при параллельных АС и МО и секущей СВ.

/ МDВ = / МОN, как соответственные углы при параллельных СВ и ОN и секущей МО, но тогда и / АСВ = / МОN.

Следовательно, углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые.

Построим два острых угла АСВ и МОN с соответственно параллельными сторонами (черт. 213): СА || МО и СВ || ОN, и продолжим за вершину О стороны угла МОN.

При вершине О образовались два гупых угла ЕОМ и FОN (так как смежный с ними угол МОN по построению острый).

Каждый из них в сумме с углом МОN составляет 2d, а так как / МОN = / АСВ,
то / АСВ+ / МОЕ = 2d и / АСВ+ / FОN = 2d.

2. Углы с соответственно перпендикулярными сторонами.

Построим произвольный острый угол АВС. Проведём через вершину угла лучи, перпендикулярные к его сторонам, так, чтобы они образовали острый угол.

BO_|_ ВС и ВК _|_ АВ (черт. 214). Мы получим новый угол OBK.
Стороны углов AВС и ОВК взаимно перпендикулярны.

Отсюда следует, что / АBС = / ОВК.

Построим произвольный тупой угол АОВ и через его вершину проведём лучи, перпендикулярные к его сторонам, так, чтобы они образовали тупой угол.
ОК_|_ОА и ОС_|_ОВ (черт. 215), угол КОС — тупой. Стороны углов АОВ и КОС взаимно перпендикулярны, поэтому

Отсюда следует, что / АОВ = / КОС.

Углы с соответственно перпендикулярными сторонами равны между собой, если они оба острые или оба тупые.

Построим произвольный острый угол АОВ и проведём через его вершину перпендикуляры к его сторонам так, чтобы они образовали острый угол (черт. 216).
Получим: / КОМ = / АОВ. Продолжим сторону ОК за вершину О. Стороны угла ЕОМ перпендикулярны сторонам угла АОВ. При этом / ЕОМ — тупой, так как смежный с ним / МОК — острый. / КОМ + / ЕОМ = 2d (как углы смежные). Но / КОМ по ранее доказанному равен / АОВ. Следовательно, и / АОВ + / ЕОМ = 2d.

Углы с соответственно перпендикулярными сторонами в сумме составляют 2d, если один из них острый, а другой тупой.

Мы рассматривали углы, составленные взаимно перпендикулярными сторонами, когда они имели общую вершину. Выведенные нами свойства будут справедливы и в том случае, когда углы не будут иметь общей вершины.

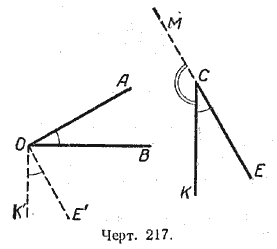
Построим произвольный острый угол АОВ и через какую-нибудь точку С (черт. 217) проведём лучи СЕ __|_ОA и СК _|_ ОВ так, чтобы угол КСЕ был тоже острый.

Углы АОВ к КСЕ составлены взаимно перпендикулярными сторонами. Докажем, что они равны между собой. Для этого через точку О (вершину / АОВ) проведём ОК’||СК и ОЕ’ || СЕ. / КСЕ = / КОЕ’, так как они составлены взаимно параллельными сторонами и оба острые. Но / К’ОЕ’ = / АОВ по доказанному. Следовательно, / АОВ = / КСЕ.

Если продолжим сторону СЕ за вершину угла, мы получим / МСК, смежный с / КСЕ.
/ МСК + / КСЕ = 2d, но / КСЕ = / АОВ, Поэтому / АОВ + / МСК = 2d.

Источник

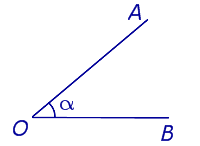
Углы на плоскости

Схему обозначения углов рассмотрим на примере угла, изображенного на рисунке 1.

Изображенный на рисунке 1 угол можно обозначить тремя способами:

Углы называют равными углами, если их можно совместить.

Углом в 1° (один градус) называют угол, составляющий одну девяностую часть прямого угла.

Таблица 1 – Типы углов в зависимости от величины в градусах

Прямой угол равен 90°

Острый угол

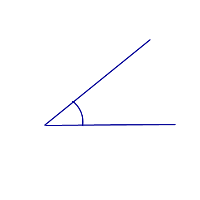
Острый угол меньше 90°

Тупой угол

Развернутый угол

Развернутый угол равен 180°

Угол больший, чем развернутый

Полный угол

Полный угол равен 360°

Угол, равный нулю

Такой угол равен 0°

Таблица 2 – Типы углов в зависимости расположения сторон

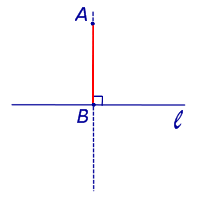
Свойство вертикальных углов:

Вертикальные углы равны

Смежные углы

Свойство смежных углов:

Сумма смежных углов равна 180°

Углы с соответственно параллельными сторонами

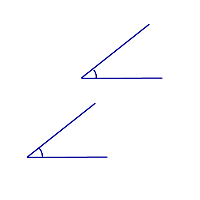
Свойство углов с соответственно параллельными сторонами:

Углы с соответственно параллельными сторонами равны, если оба являются острыми или оба являются тупыми

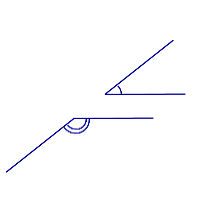
Свойство углов с соответственно параллельными сторонами:

Углы с соответственно перпендикулярными сторонами

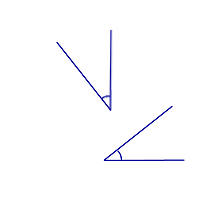
Свойство углов с соответственно перпендикулярными сторонами:

Углы с соответственно перпендикулярными сторонами равны, если оба являются острыми или оба являются тупыми

Свойство углов с соответственно перпендикулярными сторонами:

На этом рисунке углы AOB и BOC – смежные, а лучи OE и OD – биссектрисы этих углов. Поскольку

Источник