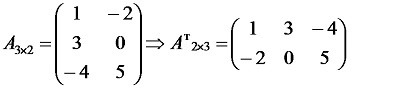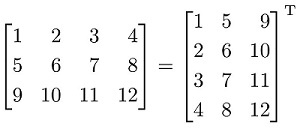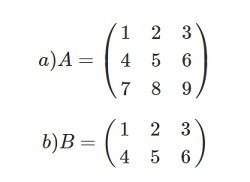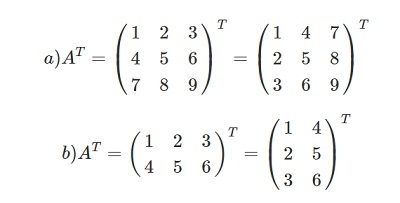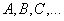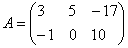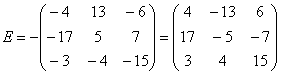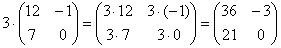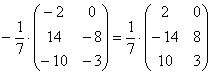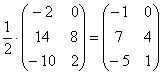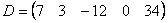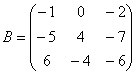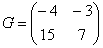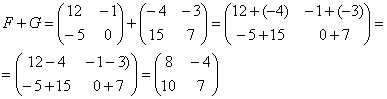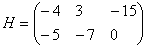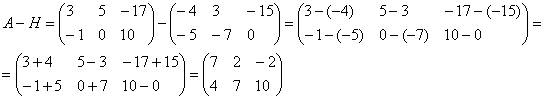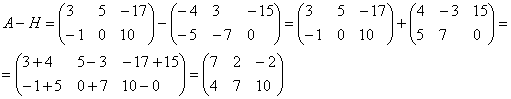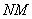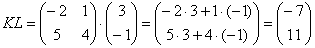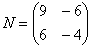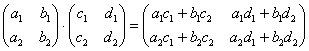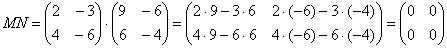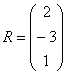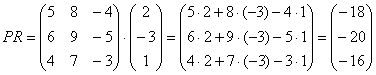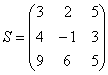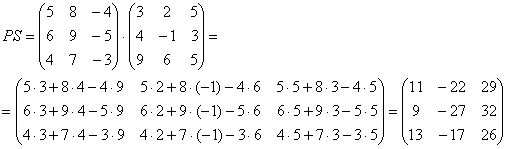Что значит транспонированная матрица
Транспонирование матрицы
Обновлено: 19 Июля 2021
Нам уже знакомо понятие матрицы. Этот математический объект имеет прикладное значение: он позволяет структурировать числа и информацию, проводить сложные расчёты. С ним можно проделывать различные операции, и одной из них является транспортирование.
Что такое транспонированная матрица, в чем отличие от обычной
Транспонирование – это алгоритм, при котором m-строки меняются местами с n-столбцами.
Транспонированная матрица, в отличие от обычной, помогает получить одинаковый результат при умножении на вектор-столбец и вектор-строку, что значительно упрощает дальнейшие математические вычисления.
Особенности, определитель и свойства целочисленных
Свойства транспортирования целочисленных матриц:
Если матрица А – квадратная (m=n), то определитель исходной и транспортированной матрицы равны: det A T = det A.
Напомним, что определитель – это некоторое число, с которым можно сравнить любую квадратную матрицу.
Формула, как обозначается транспонированная матрица
Тогда формула для транспортировки выглядит следующим образом:
A T ij = A ji
Формально, если А = m × n, то A T = n × m, но математически это записывается через индексы i и j.
Примеры задач на транспонирование матриц
Само транспортирование – довольно лёгкий процесс. Рассмотрим один пример.
Задача: даны А = (m × n) и В = (m × n).
Необходимо выполнить транспортирование.
Произведение и сумма транспонированных матриц
Теорема: транспонирование произведения матриц равно произведению транспонированных матриц, взятых в обратном порядке.
В математическом виде теорема выглядит так:
С T = (A · B) T = В T · А T
Сумма вычисляется по аналогичной формуле:
C T = (A + B) T = A T + В T
Периодически возникают сложности с учебой? ФениксХэлп может помочь!
Действия с матрицами
Данное методическое пособие поможет Вам научиться выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>>.
Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами.
Для СВЕРХБЫСТРОЙ подготовки по теме (у кого «горит») есть интенсивный pdf-курс Матрица, определитель и зачёт!
Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.
Обозначение: матрицы обычно обозначают прописными латинскими буквами 
Пример: рассмотрим матрицу «два на три»:
Данная матрица состоит из шести элементов: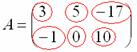 
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет: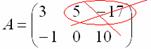 
Это просто таблица (набор) чисел!
Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!
Рассматриваемая матрица имеет две строки: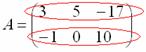 
и три столбца: 
СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: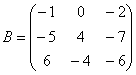 
– матрица «три на три».
Если в матрице один столбец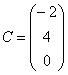 
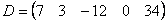
или одна строка 
, то такие матрицы также называют векторами.
На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: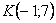 
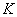
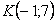
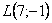
. По существу, координаты точки 
записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение: 
и 
– это две совершенно разные точки плоскости.
Теперь переходим непосредственно к изучению действий с матрицами:
1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Вернемся к нашей матрице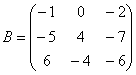 
. Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак: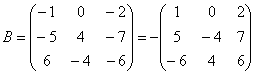 
У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.
Обратный пример: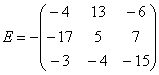 
. Выглядит безобразно.
Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:
Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.
2) Действие второе. Умножение матрицы на число.
Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
Еще один полезный пример:
– умножение матрицы на дробь
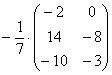
Сначала рассмотрим то, чего делать НЕ НАДО: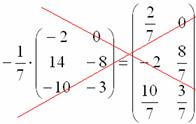 
Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если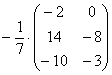 
– окончательный ответ задания).
И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:
Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.
Единственное, что желательно сделать в этом примере – это внести минус в матрицу:
А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
В этом случае можно и НУЖНО умножить все элементы матрицы на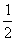 
, так как все числа матрицы делятся на 2 без остатка.
Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.
3) Действие третье. Транспонирование матрицы.
Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.
Транспонировать матрицу 
Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:
– транспонированная матрица.
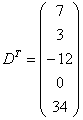
Транспонированная матрица обычно обозначается надстрочным индексом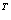 
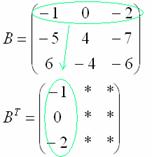
или штрихом справа вверху.
Транспонировать матрицу 
Сначала переписываем первую строку в первый столбец:
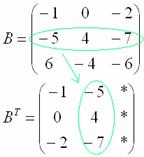
Потом переписываем вторую строку во второй столбец: 
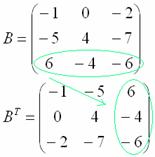
И, наконец, переписываем третью строку в третий столбец:
Готово. Образно говоря, транспонировать – это значит взять матрицу за правый верхний угол и аккуратно повернуть её «на себя» по диагонали, «стряхивая» числа в столбцы транспонированной матрицы. Такая вот у меня ассоциация.
4) Действие четвертое. Сумма (разность) матриц.
Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой! 
Сложить матрицы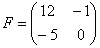 
и 
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.
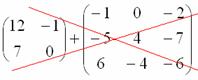
Найти разность матриц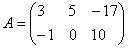 
, 
А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу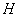 
:
Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.
5) Действие пятое. Умножение матриц.
Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.
Какие матрицы можно умножать?
Чтобы матрицу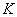 
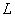
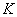
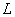
можно было умножить на матрицу 
нужно, чтобы число столбцов матрицы 
равнялось числу строк матрицы 
.
Пример:
Можно ли умножить матрицу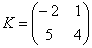 
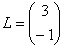
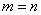
на матрицу 
?
, значит, умножать данные матрицы можно.
А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!
, следовательно, выполнить умножение невозможно:
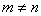
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.
Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц,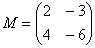 
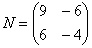
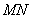
и 
возможно как умножение 
, так и умножение 
Как умножить матрицы?
Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.
Начнем с самого простого:
Умножить матрицу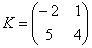 
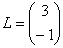
на матрицу 
Я буду сразу приводить формулу для каждого случая:
– попытайтесь сразу уловить закономерность.
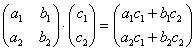
Умножить матрицу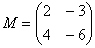 
на матрицу 
Формула: 
В результате получена так называемая нулевая матрица.
Попробуйте самостоятельно выполнить умножение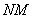 
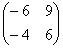
(правильный ответ 
).
Обратите внимание, что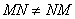 
! Это почти всегда так!
Таким образом, при умножении переставлять матрицы нельзя!
Если в задании предложено умножить матрицу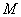 
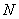
на матрицу 
, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
Переходим к матрицам третьего порядка:
Умножить матрицу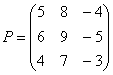 
на матрицу 
Формула очень похожа на предыдущие формулы: 
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте матрицу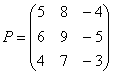 
на матрицу 
Вот готовое решение, но постарайтесь сначала в него не заглядывать!
Данная тема достаточно обширна, и я вынес этот пункт на отдельную страницу.
А пока спектакль закончен.
После освоения начального уровня рекомендую отработать действия с матрицами на уроке Свойства операций над матрицами. Матричные выражения.
Автор: Емелин Александр
(Переход на главную страницу)
Zaochnik.com – профессиональная помощь студентам
cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5
Tutoronline.ru – онлайн репетиторы по математике и другим предметам
Смысл транспонированной матрицы
Сравнить след матрицы со следом транспонированной матрицы
Дана квадратная матрица порядка N. Получить транспонированную матрицу. Сравнить сумму элементов.
Прибавление транспонированной матрицы
Ребят помогите пожалуйста.У меня есть матрица и её транспонированная версия.Как мне их прибавить? У.
Используя программу вычисления транспонированной матрицы S^T
Помогите решить задачу на С++: Используя программу вычисления транспонированной матрицы S^T.
Плюсую про инструмент. Матрицы применяются в разных дисциплинах, поэтому матрица может допускать разные интерпретации — как линейный оператор, или квадратичная форма, или матрица перехода, или система уравнений, или (покидаем линейную алгебру) как матрица смежности или инцидентности графа, или цепь Маркова, или план перевозок в транспортной теории. Но это всё интерпретации, а матрицы существуют сами по себе. Утверждение о матрицах может допускать разные интерпретации. Напрашивающийся пример: утверждение «для любой симметрической матрицы A найдётся ортогональная матрица O, такая, что матрица ортогональна» может быть интерпретировано в виде геометрической теоремы: «самосопряжённый оператор на евклидовом пространстве имеет базис из собственных векторов» или алгебраической теоремы о многочленах «квадратичную форму с вещественными коэффициентами можно привести к диагональному виду ортогональным преобразованием».
Что касается интерпретации транспонирования в линейной алгебре, мне кажется, оно, как и двумерность матрицы, наиболее естественно согласуется с дуальностью. Например, если A — матрица линейного оператора в каком-то базисе, то транспонированная матрица A’ является матрицей сопряжённого оператора в дуальном базисе. Или если T — матрица перехода от базиса e к базису f, то транспонированная T’ — матрица перехода от базиса, дуального к f, к базису, дуальному к e.
Добавлено через 2 минуты
А, и с той точки зрения, что матрица — «таблица вида», операция транспонирования совершенно естественна. Что, в конце концов, можно сделать с таблицей? Перевернуть — одно из простейших действий.
Спасибо за ответы! Темрин дуальность встречал уже где-то, думаю нужно в этом направлении копать.
Нашел очень неплохие, хорошо иллюстрированные лекции. Вот конкретно в этом уроке автор на пальцах объясняет, что скалярное произведение векторов a и b равно произведению транспонированного вектора на a на b и говорит, что для каждого некого вектора в одном линейном пространстве, соответствует другой вектор в другом линейном пространстве, и как раз это и есть дуальность. :
Может по аналогии можно найти и транспонированную матрицу?
Решение
Про дуальность лучше в учебнике прочитайте. В любом. В Кострикине, например. Скалярное произведение ни при чём, его обычно вообще нет. Общий смысл, что пространство и его сопряжённое можно рассматривать как пару равноценных пространств, соединённых спариванием.
Вообще, я, конечно, не могу почитать за вас учебники, но если что непонятно, попробую пояснить. В линейной алгебре часто бывает, что материал кажется абсолютно непонятным, а если разобраться ― совершенно очевидным.
Приведу примеры матричного формализма. Для определённости буду писать над R, но поле непринципиально.
Сказанное применимо к любому конечномерному пространству, в котором выбран базис. Тогда координаты векторов записываем как столбцы, а координаты функционалов в дуальном базисе ― как строки.
Немного насчёт скалярного произведения. Теорема Рисса позволяет канонически отождествить евклидово пространство со своим сопряжённым: вектору x ставится в соответствие функционал скалярного умножения на x. В паре пространств и это отождествление является ни чем иным как транспонированием. В самом деле, давайте поймём, какой функционал соответствует по теореме Рисса вектору
На произвольный вектор
Сказанное имеет смысл и для любого евклидова пространства, в котором выбран ортонормированный базис.
Моё утверждение о транспонированной матрице перехода попробуйте доказать в качестве упражнения.