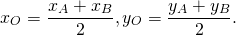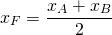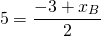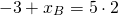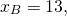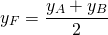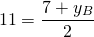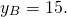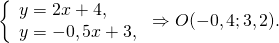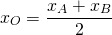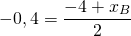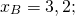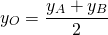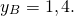Что значит точки симметричны относительно другой точки
ВИДЫ СИММЕТРИИ
СИММЕТРИЯ ОТНОСИТЕЛЬНО ПРЯМОЙ (ОСЕВАЯ СИММЕТРИЯ)
Одна точка называются симметричной другой относительно прямой, если данная прямая проходит через середину отрезка, соединяющего эти точки, и перпендикулярна к этому отрезку. Каждая точка прямой а считается симметричной самой себе. Прямая называется осью симметрии фигуры если каждая точка фигуры симметрична относительно некоторой точки той же фигуры.
зеркальная симметрия
Геометрическая фигура называется симметричной относительно плоскости S, если для каждой точки этой фигуры может быть найдена другая точка этой же фигуры, так что отрезок, соединяющий эти точки, перпендикулярен плоскости S и делится этой плоскостью пополам. Плоскость S называется плоскостью симметрии.
Симметричные фигуры, предметы и тела не равны друг другу в узком смысле слова (например, левая перчатка или ботинок не подходит для правой руки или ноги и наоборот). Они называются зеркально равными.
центральная симметрия
Геометрическая фигура (или тело) называется симметричной относительно центра О, если для каждой точки этой фигуры может быть найдена другая точка этой же фигуры, так что отрезок, соединяющий эти точки, проходит через центр О и делится в этой точке пополам. Точка О называется центром симметрии.
поворотная симметрия (симметрия вращения)
При поворотной симметрии переход частей фигуры в новое положение или преобразование исходной фигуры происходит при повороте фигуры на определенный угол вокруг точки, которая называется центром поворота. Поворотная симметрия может рассматриваться на плоскости и в пространстве.
Тело (фигура) обладает симметрией вращения, если при повороте на угол 360°/n (n – целое число, например, 2, 3, 4 и т.д. до бесконечности) вокруг некоторой прямой (оси симметрии) оно полностью совпадает со своим начальным положением. При n = 2 мы имеем осевую симметрию.
симметрия подобия
Представляет собой своеобразный аналог предыдущих симметрий с той лишь разницей, что она связана с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрешки.
переносная (трансляционная симметрия)
О такой симметрии говорят тогда, когда при переносе фигуры вдоль прямой на какое-то расстояние, либо расстояние, кратное этой величине, она совмещается сама с собой. Прямая, вдоль которой производится перенос, называется осью переноса.
примеры симметрии геометрических фигур
Разными видами симметрии могут обладать и плоские и объемные фигуры. Например, квадрат, прямоугольник, ромб имеют и центр симметрии и оси симметрии.
Окружность и круг имеют центр симметрии и бесконечно много осей симметрии. Объемные фигуры могут иметь центр симметрии, оси симметрии и обладать зеркальной симметрией.
Правильные многогранники своей симметрией с древних времён привлекали к себе внимание учёных, архитекторов, художников. Их по праву называют самыми симметричными из всех многогранников.
Подробно описал свойства правильных многогранников древнегреческий учёный Платон. Поэтому их называют телами Платона. Правильным многогранникам посвящена 13 книга “Начал” Евклида.
Очень симметричной фигурой является, например, куб. Центром симметрии куба является точка пересечения его диагоналей. Через центр симметрии проходят 9 осей симметрии. Плоскостей симметрии у куба также 9 и проходят они либо через противоположные ребра (6), либо через середины противоположных ребер (3).
Через центр симметрии проходят 9 осей симметрии. Плоскостей симметрии у куба также 9 и проходят они либо через противоположные ребра (6), либо через середины противоположных ребер (3).
Координаты симметричных точек
Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.
По формулам координаты середины отрезка получаем связь координат этих точек:
Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.
То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от координат точки A только знаками:
A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.
1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).
Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда
2) Найти точку, симметричную точке C (9;-4) относительно начала координат.
Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).
II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.
Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:
Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.
Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:
Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.
Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.
Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:
Осевая и центральная симметрия
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Симметрия фигур в пространстве
Центральная симметрия
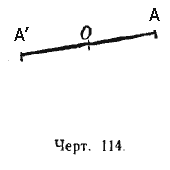
Две фигуры называются симметричными относительно какой-либо точки О пространства, если каждой точке А одной фигуры соответствует в другой фигуре точка А’, расположенная на прямой ОА по другую сторону от точки О, на расстоянии, равном расстоянию точки А от точки О (черт. 114). Точка О называется центром симметрии фигур.
Пример таких симметричных фигур в пространстве мы уже встречали (§ 53), когда, продолжая за вершину рёбра и грани многогранного угла, получали многогранный угол, симметричный данному. Соответственные отрезки и углы, входящие в состав двух симметричных фигур, равны между собой. Тем не менее фигуры в целом не могут быть названы равными: их нельзя совместить одну с другой вследствие того, что порядок расположения частей в одной фигуре иной, чем в другой, как это мы видели на примере симметричных многогранных углов.
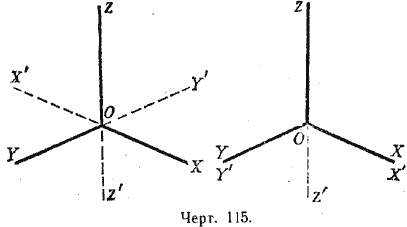
В отдельных случаях симметричные фигуры могут совмещаться, но при этом будут совпадать несоответственные их части. Например, возьмём прямой трёхгранный угол (черт. 115) с вершиной в точке О и рёбрами ОХ, OY, OZ.
Построим ему симметричный угол ОХ’Y’Z’. Угол OXYZ можно совместить с OX’Y’Z’ так, чтобы ребро ОХ совпало с OY’, а ребро OY c OX’. Если же совместить соответственные рёбра ОХ с ОХ’ и OY с OY’, то рёбра OZ и OZ’ окажутся направленными в противоположные стороны.
Правильный тетраэдр не имеет центра симметрии.
Симметрия относительно плоскости
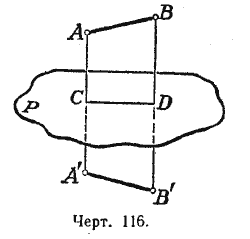
Две пространственные фигуры называются симметричными относительно плоскости Р, если каждой точке А в одной фигуре соответствует в другой точка А’, причём отрезок АА’ перпендикулярен к плоскости Р и в точке пересечения с этой плоскостью делится пополам.
Теорема. Всякие два соответственных отрезка в двух симметричных фигурах равны между собой.
Если какое-либо геометрическое тело можно разбить на две части, симметричные относительно некоторой плоскости, то эта плоскость называется плоскостью симметрии данного тела.
Геометрические тела, имеющие плоскость симметрии, чрезвычайно распространены в природе и в обыденной жизни. Тело человека и животного имеет плоскость симметрии, разделяющую его на правую и левую части.
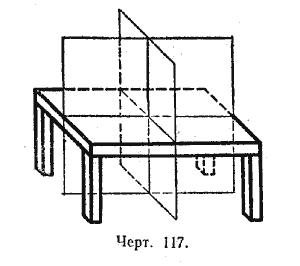
На этом примере особенно ясно видно, что симметричные фигуры нельзя совместить. Так, кисти правой и левой рук симметричны, но совместить их нельзя, что можно видеть хотя бы из того, что одна и та же перчатка не может подходить и к правой и к левой руке. Большое число предметов домашнего обихода имеет плоскость симметрии: стул, обеденный стол, книжный шкаф, диван и др. Некоторые, как например обеденный стол, имеют даже не одну, а две плоскости симметрии (черт. 117).
Обычно, рассматривая предмет, имеющий плоскость симметрии, мы стремимся занять по отношению к нему такое положение, чтобы плоскость симметрии нашего тела, или по крайней мере нашей головы, совпала с плоскостью симметрии самого предмета. В этом случае симметричная форма предмета становится особенно заметной.
Симметрия относительно оси. Ось симметрии второго порядка.
Из этого определения непосредственно следует, что если два геометрических тела, симметричных относительно какой-либо оси, пересечь плоскостью, перпендикулярной к этой оси, то в сечении получатся две плоские фигуры, симметричные относительно точки пересечения плоскости с осью симметрии тел.
Отсюда далее легко вывести, что два тела, симметричных относительно оси, можно совместить одно с другим, вращая одно из них на 180° вокруг оси симметрии. В самом деле, вообразим все возможные плоскости, перпендикулярные к оси симметрии.
Каждая такая плоскость, пересекающая оба тела, содержит фигуры, симметричные относительно точки встречи плоскости с осью симметрии тел. Если заставить скользить секущую плоскость саму по себе, вращая её вокруг оси симметрии тела на 180°, то первая фигура совпадает со второй.
Это справедливо для любой секущей плоскости. Вращение же всех сечений тела на 180° равносильно повороту всего тела на 180° вокруг оси симметрии. Отсюда и вытекает справедливость нашего утверждения.
Если после вращения пространственной фигуры вокруг некоторой прямой на 180° она совпадает сама с собой, то говорят, что фигура имеет эту прямую своею осью симметрии второго порядка.
Название «ось симметрии второго порядка » объясняется тем, что при полном обороте вокруг этой оси тело будет в процессе вращения дважды принимать положение, совпадающее с исходным (считая и исходное). Примерами геометрических тел, имеющих ось симметрии второго порядка, могут служить:
1) правильная пирамида с чётным числом боковых граней; осью её симметрии служит её высота;
2) прямоугольный параллелепипед; он имеет три оси симметрии: прямые, соединяющие центры его противоположных граней;
3) правильная призма с чётным числом боковых граней. Осью её симметрии служит каждая прямая, соединяющая центры любой пары её противоположных граней (боковых граней и двух оснований призмы). Если число боковых граней призмы 2k, то число таких осей симметрии будет k + 1. Кроме того, осью симметрии для такой призмы служит каждая прямая, соединяющая середины её противоположных боковых рёбер. Таких осей симметрии призма имеет А.
Таким образом, правильная 2k-гранная призма имеет 2k+1 осей, симметрии.
Зависимость между различными видами симметрии в пространстве.
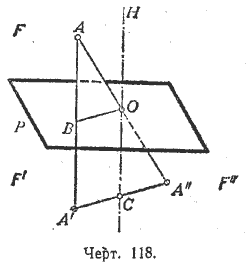
Теорема. Если фигура F симметрична с фигурой F’ относительно плоскости Р и в то же время симметрична с фигурой F» относительно точки О, лежащей в плоскости Р, то фигуры F’ и F» симметричны относительно оси, проходящей через точку О и перпендикулярной к плоскости Р.
Возьмём какую-нибудь точку А фигуры F (черт. 118). Ей соответствует точка А’ фигуры F’ и точка А» фигуры F» (сами фигуры F, F’ и F» на чертеже не изображены).
Оси симметрии высших порядков
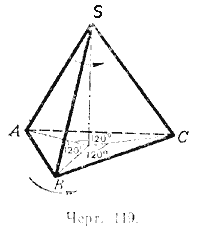
Фигура, имеющая ось симметрии, совмещается сама с собой после поворота вокруг оси симметрии на угол в 180°. Но возможны случаи, когда фигура приходит к совмещению с исходным положением после поворота вокруг некоторой оси на угол, меньший 180°. Таким образом, если тело сделает полный оборот вокруг этой оси, то в процессе вращения оно несколько раз совместится со своим первоначальным положением. Такая ось вращения называется осью симметрии высшего порядка, причём число положений тела, совпадающих с первоначальным, называется порядком оси симметрии. Эта ось может и не совпадать с осью симметрии второго порядка. Так, правильная треугольная пирамида не имеет оси симметрии второго порядка, но её высота служит для неё осью симметрии третьего порядка. В самом деле, после поворота этой пирамиды вокруг высоты на угол в 120° она совмещается сама с собой (черт. 119).
При вращении пирамиды вокруг высоты она может занимать три положения, совпадающие с исходным, считая и исходное. Легко заметить, что всякая ось симметрии чётного порядка есть в то же время ось симметрии второго порядка.
Примеры осей симметрии высших порядков:
1) Правильная n-угольная пирамида имеет ось симметрии n-го порядка. Этой осью служит высота пирамиды.
2) Правильная n-угольная призма имеет ось симметрии n-го порядка. Этой осью служит прямая, соединяющая центры оснований призмы.
Симметрия куба.
Куб имеет девять плоскостей симметрии: шесть диагональных плоскостей и три плоскости, проходящие через середины каждой четвёрки его параллельных рёбер.
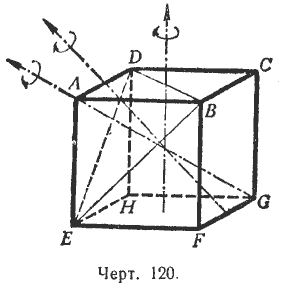
Куб имеет девять осей симметрии второго порядка: шесть прямых, соединяющих середины его противоположных рёбер, и три прямые, соединяющие центры противоположных граней (черт. 120).
Эти последние прямые являются осями симметрии четвёртого порядка. Кроме того, куб имеет четыре оси симметрии третьего порядка, которые являются его диагоналями. В самом деле, диагональ куба АG (черт. 120), очевидно, одинаково наклонена к рeбрам АВ, АD и АЕ, а эти рёбра одинаково наклонены одно к другому. Ecли соединить точки В, D и Е, то получим правильную треугольную пирамиду АDВЕ, для которой диагональ куба AG служит высотой. Когда при вращении вокруг высоты эта пирамида будет совмещаться сама с собой, весь куб будет совмещаться со своим исходным положением. Других осей симметрии, как нетрудно убедиться, куб не имеет. Посмотрим, сколькими различными способами куб может быть совмещён сам с собой. Вращение вокруг обыкновенной оси симметрии даёт одно положение куба, отличное от исходного, при котором куб в целом совмещается сам с собой.
Легко убедиться непосредственно, что все эти положения отличны одно от другого, а также и от исходного положения куба. Вместе с исходным положением они составляют 24 способа совмещения куба с самим собой.
Что такое симметрия относительно точки?
Как найти точку симметричную точке относительно точки?
Что значит симметричен относительно точки?
Симметрия относительно точки
Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре. Точка A называется центром симметрии фигуры.
Как найти симметрию треугольника?
1) Провести из точки A к прямой g перпендикуляр AO. 2) На продолжении перпендикуляра с другой стороны от прямой g отложить отрезок OA1, равный отрезку AO: OA1=AO. Полученная точка A1 симметрична точке A относительно прямой g. Прямая g называется осью симметрии.
Как провести осевую симметрию?
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой. При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Когда точки симметричны?
в) начала координат. Две точки M1 и M2 называются симметричными относительно прямой, если отрезок M1M2 перпендикулярен этой прямой, причем его середина лежит на этой прямой. Две точки M1 и M2 называются симметричными относительно точки O, если точка O является серединой отрезка M1M2.
Как найти симметричную точку относительно центра?
Как строить симметричные точки?
Чтобы построить точку А1, симметричную А относительно прямой, постройте луч с начальной точкой А, пересекающийся с прямой и перпендикулярный ей. Измерьте расстояние от А до точки пересечения прямой и луча, а затем постройте точку А1 на том же расстоянии от прямой, но в противоположной стороне.
Что значит фигура имеет центр симметрии или ось симметрии?
Свойство: Фигуры, симметричные относительно некоторой точки, равны. Фигура симметрична относительно центра симметрии, если для каждой этой точки фигуры симметричная ей точка также лежит на этой фигуре. Такая фигура имеет центр симметрии (фигура с центральной симметрией).
Какая фигура имеет ось симметрии но не имеет центра симметрии?
С другой стороны, существуют фигуры, не имеющие центров и осей симметрии. Например, тетраэдр не имеет ни одного центра симметрии.
Какая фигура имеет центр симметрии и ось симметрии равносторонний треугольник?
Ответ: Центр симметрии и ось симметрии у фигуры под А) равносторонний треугольник.