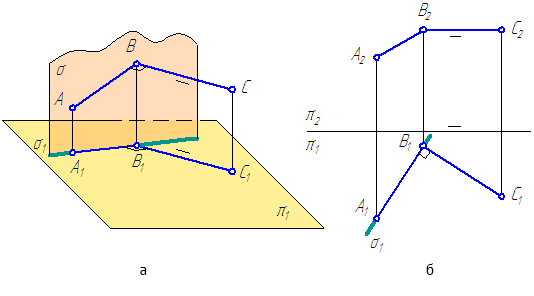
Что значит точка принадлежит прямой на эпюре

Принадлежность точки прямой линии

Если точка принадлежит прямой, то ее проекции принадлежат одноименным проекциям этой прямой. Обратное заключение справедливо для всех прямых кроме профильных уровня.

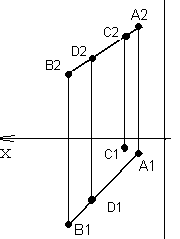
Рис. 30. Эпюр прямой

Проекции точки D лежат на одноименных проекциях прямой АВ, следовательно, точка D принадлежит прямой АВ (рис. 30). Фронтальная проекция точки С принадлежит фронтальной проекции прямой АВ, а горизонтальная проекция С₁ не лежит на горизонтальной проекции прямой АВ, следовательно, точка С не принадлежит прямой АВ.

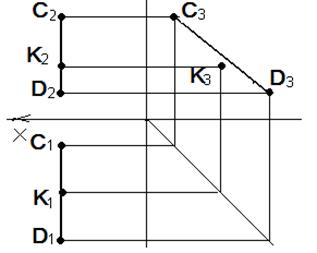
На рис. 31 изображена профильная прямая CD. Точка К расположена таким образом, что ее горизонтальная проекция К₁ принадлежит горизонтальной проекции прямой C₁D₁, а фронтальная проекция К₂ принадлежит фронтальной проекции прямой. Тем не менее, чтобы сделать вывод о принадлежности точки К прямой CD, необходимо построить их третьи проекции – профильные. По чертежу видно, что профильная проекция точки К₃ не лежит на профильной проекции прямой, следовательно, и сама точка не принадлежит прямой. Для всех других прямых, кроме профильной уровня, достаточно проверить принадлежность двух проекций точки одноименным проекциям прямой.

Рис. 31. Профильная прямая

Взаимное положение прямых

2) быть параллельными (лежать в одной плоскости и не иметь общей точки);

3) скрещиваться (лежать в разных плоскостях и не иметь общей точки).

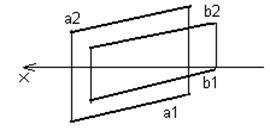
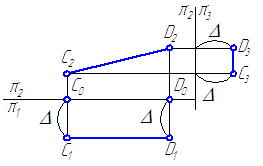
Если прямые параллельны, то одноименные проекции двух параллельных прямых параллельны между собой.

Рис. 32. Эпюр параллельных прямых а и b

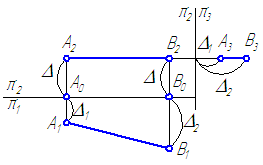
Если прямые пересекаются, то их одноименные проекции пересекаются между собой, а проекции точки пересечения лежат на одной линии связи.

Скрещивающиеся прямые – прямые, которые не пересекаются и не параллельны между собой. На эпюре скрещивающиеся прямые будут напоминать пересекающиеся с той лишь разницей, что точки пересечения фронтальных и горизонтальных проекций не будут лежать на одной линии связи (перпендикуляре к оси ОХ).

Рис. 34. Скрещивающиеся прямые

Точки, лежащие на одном проецирующем луче, называются конкурирующими.

Рис. 35. Конкурирующие точки и определение их видимости на П₁ и П₂, невидимые точки берутся в скобки

Плоскости

Плоскость в пространстве определяется:

1) тремя точками, не лежащими на одной прямой;

2) прямой и точкой не принадлежащей ей;

3) двумя параллельными прямыми;

4) двумя пересекающимися прямыми;

5) отсеком плоской фигуры – треугольником, четырехугольником и т. д.

Рис. 36. Задание плоскости тремя точками

Рис. 37. Задание плоскости треугольником

В начертательной геометрии пользуются еще одним способом задания плоскостей – следами.

Следом плоскости называют линию пересечения плоскости с плоскостью проекций.

Плоскость Q пересекается с плоскостями проекций по прямым, называемым следами плоскости: Q₁ – горизонтальный след плоскости, Q₂ – фронтальный, Q₃ – профильный след плоскости. Q_x, Q_y, Q_z – точки схода следов на осях проекций.

Рис. 38. Изображение плоскости

Рис. 39. Эпюр плоскости

Часто плоскость на эпюре изображается двумя следами (Q₁, Q₂), которые как две пересекающиеся прямые вполне определяют плоскость. Фронтальный след плоскости расположен во фронтальной плоскости проекций, поэтому его горизонтальная проекция лежит на оси ОХ. Горизонтальный след плоскости расположен в горизонтальной плоскости проекций, его фронтальная проекция лежит на оси ОХ.

Плоскость, не перпендикулярная ни одной из плоскостей проекций, называется плоскостью общего положения. Плоскость общего положения пересекается со всеми плоскостями проекций, т. к. не параллельна ни одной из них.

Плоскости, перпендикулярные одной какой-либо плоскости проекций, называются проецирующими.

Плоскость, перпендикулярная горизонтальной плоскости проекций называется горизонтально проецирующей. Если эта плоскость задана следами, то ее фронтальный след всегда перпендикулярен оси ОХ, а горизонтальный след составляет с осью ОХ угол β, который является углом наклона данной плоскости к фронтальной плоскости проекций П₂.

Рис. 40. Горизонтально проецирующая плоскость, заданная следами

Если горизонтально проецирующая плоскость задана треугольником, то горизонтальная проекция треугольника вырождается в прямую линию.

Рис. 41. Горизонтально проецирующая плоскость, заданная треугольником АВС

Плоскость, перпендикулярная фронтальной плоскости проекций, называется фронтально проецирующей. Если такая плоскость задана следами, то ее горизонтальный след всегда перпендикулярен оси ОХ, а фронтальный составляет с осью ОХ угол α, который является углом наклона данной плоскости к горизонтальной плоскости проекций.

Рис. 42. Фронтально проецирующая плоскость, заданная следами

Рис. 43. Фронтально проецирующая плоскость задана прямой t и точкой D, не лежащей на ней

Плоскость, перпендикулярная профильной плоскости проекций, называется профильно проецирующей. Оба следа плоскости, горизонтальный и фронтальный, расположены параллельно оси ОХ.

Рис. 44. Изображение профильно проецирующей плоскости

Рис. 45. Эпюр профильно проецирующей плоскости

Плоскости, параллельные какой-либо плоскости проекций, называются плоскостями уровня.

Плоскость, параллельная горизонтальной плоскости проекций, называется горизонтальной плоскостью уровня. Ее фронтальный след параллелен оси ОХ, профильный – параллелен оси OY. Горизонтального следа у этой плоскости нет, т. к. она параллельна П₁.

Рис. 46. Изображение горизонтальной плоскости уровня

Рис. 47. Эпюр горизонтальной плоскости уровня

Если горизонтальная плоскость уровня задана треугольником, то он проецируется на горизонтальную плоскость проекций в натуральную величину.

Рис. 48. Горизонтальная плоскость уровня, заданная треугольником

Плоскость, параллельная фронтальной плоскости проекций, называется фронтальной плоскостью уровня. Она не имеет фронтального следа, и все, что в ней лежит, проецируется в натуральную величину на П₂.

Рис. 49. Фронтальная плоскость уровня задана следами

Плоскость, параллельная профильной плоскости проекций, называется профильной плоскостью уровня. Такая плоскость не имеет профильного следа, а ее горизонтальный и фронтальный следы перпендикулярны оси ОХ.

Рис. 50. Плоскость профильного уровня задана следами

Если профильная плоскость уровня задана геометрической фигурой, то она проецируется в натуральную величину на П₃.

Рис. 51. Плоскость профильного уровня задана треугольником

Источник

ЭПЮР ПРЯМОЙ. ТОЧКА НА ПРЯМОЙ. ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ

Основные теоретические положения

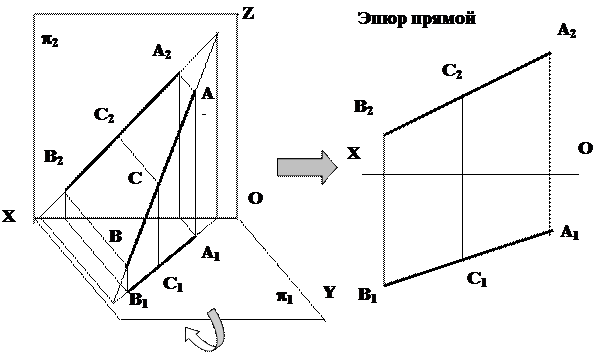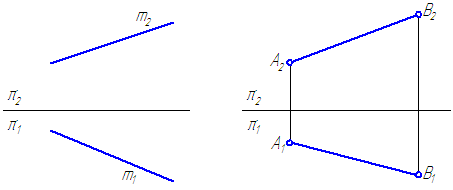
Прямая линия вполне определена двумя своими точками (не совпадающими). Проекциями прямой линии в общем случае являются также прямые линии (рис. 4.1).

Виды прямых. Прямая, произвольно расположенная в пространстве, носит название прямой общего положения. Прямые, определенным образом расположенные по отношению к плоскостям проекций носят название прямых частного положения, среди которых следует выделить (рис.3.2):

— прямая, параллельная плоскости p₁ – горизонтальная прямая (горизонаталь);

— прямая, параллельная плоскости p₂ – фронтальная прямая (фронталь);

— прямая, параллельная плоскости p₃ – профильная;

— проецирующие прямые – прямые, перпендикулярные плоскостям проекций.

Принадлежность точки прямой линии. Если точка принадлежит прямой в пространстве, то проекции этой точки на эпюре будут принадлежать одноименным проекциям прямой (точка С на рис.3.1). При ортогональном проецировании сохраняется свойство пропорциональности длин: в каком отношении точка делит отрезок прямой в пространстве, в таком же отношении ее проекции делят одноименные проекции отрезка.

Только для горизонтальных, фронтальных, а также проецирующих прямых длину отрезка и углы его наклона к плоскостям проекций можно определить по эпюру. Прямая, параллельная плоскости проекций, проецируется на эту плоскость без искажения.

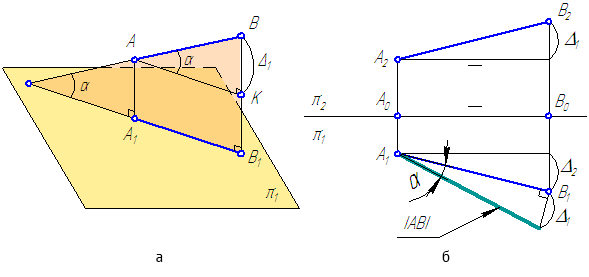
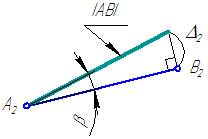
Для определения длины отрезка прямой общего положения, а также профильной прямой используют метод прямоугольного треугольника, согласно которому величина отрезка прямой определяется гипотенузой прямоугольного треугольника, одним из катетов которого является одна из проекций отрезка, а вторым – разность удаления концов отрезка от той плоскости на которой взята проекция.

Взаимное положение прямых. Прямые в пространстве могут быть параллельными, пересекающимися и скрещивающимися. если прямые в пространстветпараллельны, то на эпюре одноименные проекции этих прямых параллельны. Если прямые пересекаются, то на эпюре одноименные проекции прямых пересекаются и проекции точки пересечения лежат на одной линии связи. Если две прямые в пространстве скрещиваются, то их одноименные проекции могут пересекаться в точках, не лежащих на одной линии связи.

Прямой угол проецируется без искажения, если хотя бы одна из сторон прямого угла параллельна плоскости проекций (теорема о проецировании прямого угла).

Примеры решения задач

Задача 1. Определить натуральную величину отрезка прямой и углы его наклона к плоскостям проекций (метод прямоугольного треугольника).

Дано: Решение:

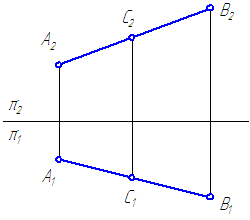
Задача 2. Разделить отрезок АВ точкой С в отношении 2:3 (рис.4.4).

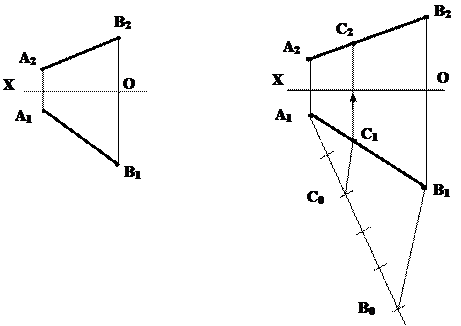Для того, чтобы построить точку С, делящую отрезок в заданном отношении, достаточно одну из проекций отрезка (на рис. 4.4) горизонтальная проекция) разделить в этом отношении, а затем построить вторую проекцию искомой точки, используя линию связи. Деление проекции А₁В₁ произведено с помощью теоремы Фалеса. Для этого из любого конца проекции А₁В₁, например из точки А₁ проводим луч под произвольным углом, на котором откладываем 2+3=5 равных отрезков произвольной длины. Соединяем точки В₀В₁, затем проводим через С₀ прямую С₀С₁||B₀B₁.

Задача 3. Достроить отрезок АВ, если длина его равна 50 мм (рис.4.5).

Задача является обратной к определению истинной величины отрезка прямой.

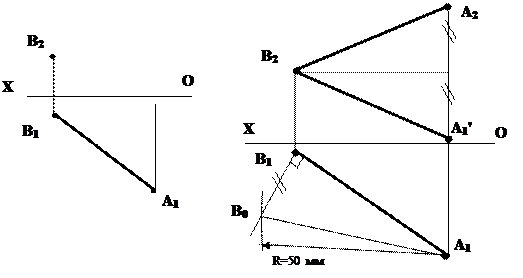
Дано: Решение:

Для того, чтобы достроить фронтальную проекцию точки A(A₂) необходимо знать разность удалений концов отрезка АВ от плоскости p₁: Dz=z_В-z_А, значение которой можно узнать, построив прямоугольной треугольник, взяв за один из катетов известную горизонтальную проекцию отрезка АВ. Треугольник построен по известному катету и гипотенузе (известной истинной величине отрезка АВ). Из прямоугольного треугольника А₁В₁В₀ находим, что Dz=|В₁В₀|. Задача имеет два решения (две точки A₂ и A’₂).

Задача 4. На прямой a (a₁,a₂) от точки А отложить отрезок АС, длиной 30 мм (рис.34.6).

На прямой а зададимся произвольным отрезком АВ. С помощью прямоугольного треугольника А₁В₁В₀ определим истинную величину отрезка АВ. Далее от точки А₁ откладываем вдоль гипотенузы заданный отрезок 30 мм. Определяем искомую точку С(С₁,С₂), используя положение о пропорциональности деления отрезка, при этом С₀С₁||В₀В₁.

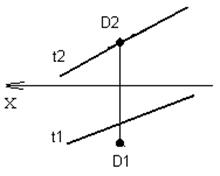
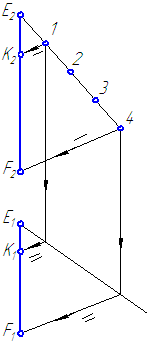
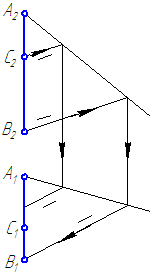
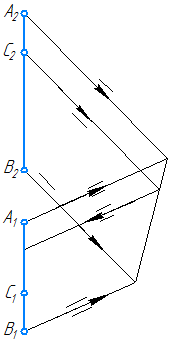
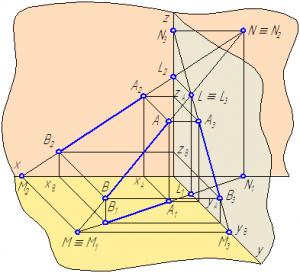
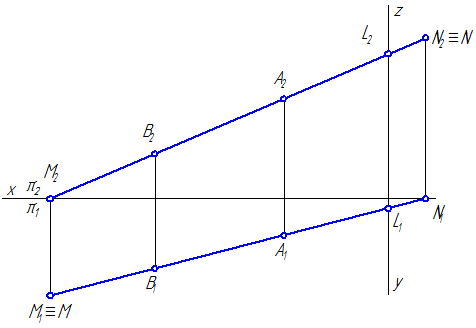
Задача 5. (Задача на профильные прямые). Достроить прямую NM, параллельную прямой КL (рис.4.7).

Замечание. Задачи на профильные прямые могут быть решены различными методами, в частности, с помощью построения третьей проекции этих прямых, либо с помощью методов косоугольного параллельного проецирования путем построения, так называемых, вспомогательных прямых. К этому типу задач следует отнести задача по определению взаимного положения профильных прямых, построения точки пересечения профильных прямых, а также ряд позиционных задач, связанных с построением точек пересечения профильной прямой и плоскости. Приведем решение задачи на профильные прямые методом построения вспомогательных прямых.

Дано: Решение:

Для того, чтобы построить недостающую фронтальную проекцию N₂ точки N, воспользуемся методом вспомогательных прямых. Суть его заключается в следующем. Для исходных профильных прямых методом косоугольного проектирования строятся вспомогательные прямые. По взаимному положению вспомогательных прямых судят о взаимном положении соответствующих им профильных прямых: если вспомогательные прямые параллельны, то параллельны соответствующие профильные прямые, если вспомогательные пересекаются, то исходные прямые или пересекаются или скрещиваются. Построим вспомогательную прямую для прямой KL. Для этого из точек K₁ и K₂ проведем лучи произвольного направления до пересечения в точке K₀. Точка К₀ – является вспомогательной для точки К. Аналогично строим точку L₀ – вспомогательную для точки L. При этом [L₁L₀)|| [K₁K₀), [L₂L₀)|| [K₂K₀). Прямая К₀L₀ является вспомогательной для прямой KL. Так как точка M, принадлежащая второй профильной прямой определена однозначно (известны обе ее проекции), построим вспомогательную ей точку М₀, при построении которой должна быть соблюдена параллельность проецирующих лучей на соответствующих проекциях: [М₁М₀)|| [K₁K₀)|| [L₁L₀) и [М₂М₀)|| [K₂K₀)|| [L₂L₀). Так как исходные прямые должны быть параллельны, поэтому через построенную точку М₀ зададим направление вспомогательной прямой М₀N₀, параллельно прямой K₀L₀. Для нахождения точки L₀ проведем проецирующий луч из точки L₁, параллельно лучам на горизонтальной проекции до пересечения с прямой, проведенной из точки M₀. Точка пересечения L₀будет являться вспомогательной для точки L, с помощью которой отыскивается неизвестная фронтальная проекция L₂ точки L.

4.3. Задачи для самостоятельного решения

Задача 1. Достроить недостающую проекцию точки С, принадлежащей отрезку АВ, а также определить истинную величину отрезка АВ и углы его на клона к плоскостям проекций (рис.4.8).

Задача 2. Построить на эпюре и в аксонометрии изображение прямой, проходящей через точки А(50,40,10) и В(25,10,30). Определить истинную величину отрезка АВ.

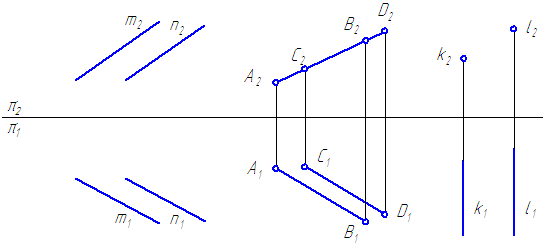
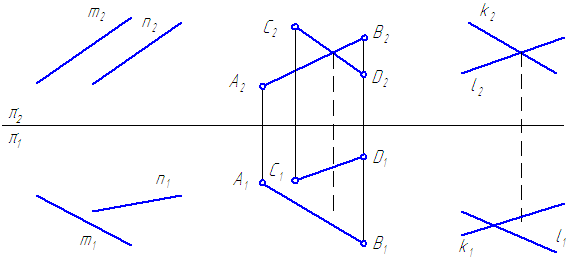
Задача 3. Определить относительное положение прямой а и точек А, В, С и D (рис.4.9).

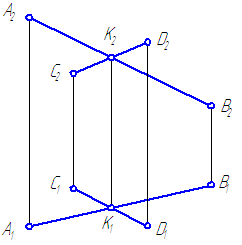
Задача 4. Определить взаимное положение прямых а и b (рис.4.10).

Рис.4.10

Задача 5. Задана прямая m||p₁. На расстоянии 30 мм от m построить прямую n||m. (При решении использовать теорему о проецировании прямого угла)(рис.4.11).

Задача 6. Через точку С провести прямую, параллельную отрезку АВ (рис.3.12).

а) б)

Задача 7. Достроить проекции треугольника АВС, если истинная величина сторон АВ=60 мм, ВС=50 мм. Определить угол наклона стороны АС к плоскости p₁ (рис.4.13).

Источник

Лекция 2. Ортогональные проекции прямой

2.1. Задание прямой на эпюре

Прямая на чертеже может быть задана изображением прямой, точкой и направлением, отрезком прямой и двумя пересекающимися плоскостями.

а б
Рисунок 2.1 – Проекции прямой

Прямоугольной проекцией отрезка в общем случае является отрезок (второе свойство центрального и параллельного проецирования). На чертеже прямая m (Рисунок 2.1, а) и отрезок АВ (Рисунок 2.1, б) произвольно наклонены к плоскостям проекций. Такие прямые называются прямыми общего положения.

Длина прямоугольной параллельной проекции отрезка общего положения всегда меньше длины самого отрезка.

2.2. Прямые частного положения

Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или горизонталью (Рисунок 2.2).

Рисунок 2.2 – Эпюр горизонтали

Если отрезок параллелен плоскости проекций π₁, то его фронтальная проекция А₂В₂ параллельна оси проекций π₁/π₂, а горизонтальная проекция отрезка А₁В₁ определяет истинную величину АВ:

Прямая, параллельная фронтальной плоскости проекций, называется фронтальной прямой или фронталью (Рисунок 2.3).

Рисунок 2.3 – Эпюр фронтали

Если отрезок параллелен плоскости проекций π₂, то его горизонтальная проекция параллельна оси проекций π₂/π₁, а фронтальная проекция отрезка C₂D₂ определяет истинную величину CD.

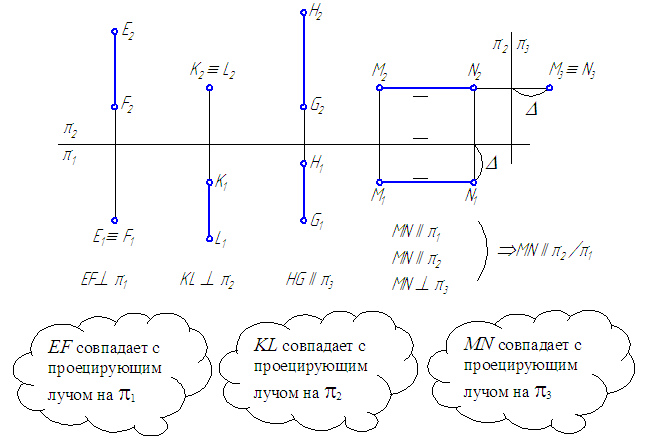
Прямая GH, параллельная профильной плоскости проекций, называется профильной прямой (Рисунок 2.4).

Прямая EF, перпендикулярная горизонтальной плоскости проекций, называется горизонтально-проецирующей (Рисунок 2.4).

Прямая KL, перпендикулярная фронтальной плоскости проекций, называется фронтально-проецирующей (Рисунок 2.4).

Прямая MN, перпендикулярная профильной плоскости проекций, называется профильно-проецирующей (Рисунок 2.4).

Рисунок 2.4 – Эпюры проецирующих прямых (EF, KL, MN) и профильной прямой GH

2.3. Метод прямоугольного треугольника

Метод прямоугольного треугольника позволяет по эпюру отрезка прямой общего положения определить его истинную величину.

Рассмотрим положение отрезка АВ относительно горизонтальной плоскости проекций π₁ (Рисунок 2.5).

Рисунок 2.5 – Определение истинной величины отрезка общего положения

АА₁ – расстояние от точки А до плоскости проекций π₁;

ВВ₁ – расстояние от точки В до плоскости проекций π₁;

ΔАКВ – прямоугольный треугольник, в котором:

ВК=ВВ₁–АА₁=Δ₁ – второй катет, равный разности расстояний от концов отрезка АВ до плоскости π₁ (то есть, разности координат Z точек А и В);

АВ – гипотенуза ΔАКВ – истинная величина.

При известных координатах концов отрезка общего положения можно на эпюре определить его истинную величину (Рисунок 2.5, б) на любой из плоскостей проекций.

Рисунок 2.6 – Определение истинной длины и угла наклона отрезка AB к плоскости проекций π₂

2.4. Точка и прямая

Если точка принадлежит прямой, то её проекции:

Рисунок 2.7 – Принадлежность точки прямой
Точка С принадлежит отрезку АВ (Рисунок 2.7), так как:

Если точка делит отрезок в каком-либо отношении, то проекции этой точки делят одноименные проекции данного отрезка в том же отношении:

Упражнение

Разделить точкой К отрезок EF в соотношении EK:KF=1:3 (Рисунок 2.8)

Рисунок 2.8 – Деление отрезка в заданном отношении
Решение:

Упражнение

Определить принадлежность точки С отрезку прямой АВ (Рисунок 2.9).

Рисунок 2.9а – Решение упражнения 2. Способ 1.

Рисунок 2.9б – Решение упражнения 2. Способ 2.

Ответ: точка С не принадлежит отрезку АВ, так как не выполняется условие принадлежности точки прямой.

2.5. Следы прямой

След прямой – точка пересечения прямой с плоскостью проекций.

Прямая общего положения в общем случае может быть три следа:

След прямой является точкой частного положения, поскольку он принадлежит плоскости проекций, следовательно, след прямой всегда совпадает с одной из своих проекций:

Рисунок 2.10 – Построение следов отрезка прямой АВ

Построим следы отрезка АВ с плоскостями проекций (Рисунки 2.10, 2.11).

Для построения горизонтального следа прямой АB необходимо:

Чтобы построить фронтальный след отрезка АB прямой, необходимо:

Ниже приводим алгоритм построения следов отрезка прямой АВ:

Рисунок 2.11 – Эпюр построения следов отрезка прямой АВ

Прямая, параллельная одной из плоскостей проекций, не имеет следа на плоскости, которой она параллельна, и пересекает только две плоскости. Прямая, параллельная двум плоскостям проекций (проецирующая прямая), имеет только один след, совпадающий с проекцией прямой на плоскость, к которой она перпендикулярна.

2.6. Взаимное расположение прямых

Две прямые в пространстве могут быть:

Параллельные прямые – прямые, пересекающиеся в несобственной точке.

Если прямые в пространстве параллельны, то их ортогональные проекции взаимно параллельны, или сливаются, или представляют собой точки, на одной из плоскостей проекций (Рисунок 2.12).

Рисунок 2.12 – Параллельные прямые
Пересекающиеся прямые – прямые, имеющие одну общую точку.

Если прямые в пространстве пересекаются, то на чертеже одноименные проекции прямых пересекаются, при этом проекции точки пересечения прямых лежат на одной линии проекционной связи и делят соответствующие проекции отрезков прямых в равных отношениях (Рисунок 2.13).

Рисунок 2.13 – Пересекающиеся прямые

Скрещивающиеся прямые – прямые, не имеющие общих точек и не удовлетворяющие признакам параллельных и пересекающихся прямых (Рисунок 2.14).

Рисунок 2.14 — Скрещивающиеся прямые

2.7. Проекции плоских углов

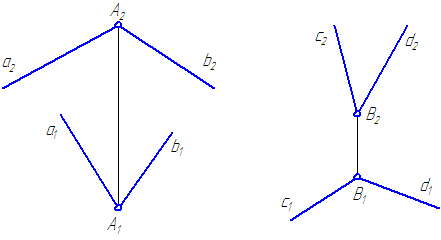
Угол между двумя пересекающимися прямыми проецируется в истинную величину, если плоскость этого угла параллельна плоскости проекций.

Рисунок 2.15

По проекциям (Рисунок 2.15) нельзя судить о величине угла между двумя прямыми. На чертежах видно, что острый угол может проецироваться в виде тупого, а тупой – в виде острого.

Теорема о проецировании прямого угла в частном случае

Рисунок 2.16 – Проецирование прямого угла

Дано: две пересекающиеся под прямым углом прямые АВ ⊥ ВС,

2.8. Задачи для самостоятельного решения

1. Построить отрезок прямой АВ // π₁, равный 35 мм и наклонённый к π₂ под углом 25° (Рисунок 2.17).

Рисунок 2.17

2. Построить отрезок прямой CD по координатам его концов С (20; 15; 30), D (70; 40; 15) и определить истинную величину отрезка и углы наклона его к плоскостям проекций π₂ и π₁.

3. Постройте проекции отрезков частного положения, расположенных под углом 30° к плоскости проекций π₁ и 45° — к плоскости проекций π₂.

4. Определите взаимное положение прямых и постройте пересечение прямых АВ и CD прямой EF//π₂/π₁ (Рисунок 2.18).

Источник