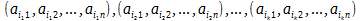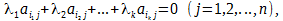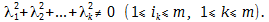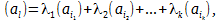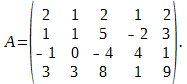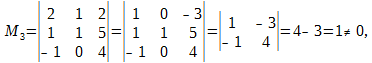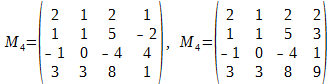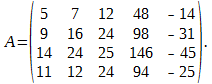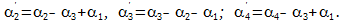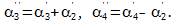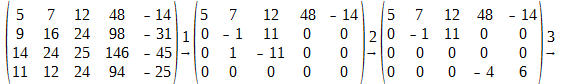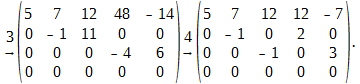Что значит строки линейно зависимы
Линейно зависимые и независимые строки.
Решение. Составим линейную комбинацию этих строк
Найдем при каких значениях α 1, α 2 эта линейная комбинация равна нулевой строке
Данное уравнение эквивалентно следующей системе уравнений:
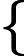 | 2 α 1 + 4 α 2 = 0 |
| 5 α 1 + 10 α 2 = 0 |
Разделим первое уравнение на 2, а второе уравнение на 5:
| α 1 + 2 α 2 = 0 |
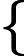| α 1 + 2 α 2 = 0 |
Решение. Составим линейную комбинацию этих строк
Найдем при каких значениях α 1, α 2 эта линейная комбинация равна нулевой строке
Данное уравнение эквивалентно следующей системе уравнений:
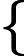| 2 α 1 + 4 α 2 = 0 |
| 5 α 1 + 10 α 2 = 0 | |
| α 1 + 0 α 2 = 0 |
Из 3-тего уравнения получаем α 1 = 0, подставим это значение в 1-ое и 2-ое уравнения:
Так как линейная комбинация строк равна нулю только когда α 1 = 0 и α 2 = 0, то строки линейно независимые.
Линейно зависимые и независимые строки: определение, примеры
В данной публикации мы рассмотрим, что такое линейная комбинация строк, линейно зависимые и независимые строки. Также приведем примеры для лучшего понимания теоретического материала.
Определение линейной комбинации строк
Линейной комбинацией (ЛК) строк s1, s2, …, sn матрицы A называется выражение следующего вида:
Если все коэффициенты αi равны нулю, значит ЛК является тривиальной. Другими словами, тривиальная линейная комбинация равняется нулевой строке.
Соответственно, если хотя бы один из коэффициентов αi не равен нулю, то ЛК является нетривиальной.
Линейно зависимые и независимые строки
Система строк является линейно зависимой (ЛЗ), если есть их нетривиальная линейная комбинация, которая равна нулевой строке.
Отсюда следует, что нетривиальная ЛК в некоторых случаях может равняться нулевой строке.
Система строк является линейно независимой (ЛНЗ), если только тривиальная ЛК равняется нулевой строке.
Примечания:
Пример задачи
Давайте выясним, является ли система строк линейно зависимой.
1. Для начала составим ЛК.
3. Составим систему уравнений:
4. Первой уравнение разделим на три, второе – на четыре:
Ответ: таким образом, строки s1 и s2 линейно зависимы.
Линейно зависимые и независимые строки.
Решение. Составим линейную комбинацию этих строк
Найдем при каких значениях α 1, α 2 эта линейная комбинация равна нулевой строке
Данное уравнение эквивалентно следующей системе уравнений:
 | 2 α 1 + 4 α 2 = 0 |
| 5 α 1 + 10 α 2 = 0 |
Разделим первое уравнение на 2, а второе уравнение на 5:
| α 1 + 2 α 2 = 0 |
| α 1 + 2 α 2 = 0 |
Решение. Составим линейную комбинацию этих строк
Найдем при каких значениях α 1, α 2 эта линейная комбинация равна нулевой строке
Данное уравнение эквивалентно следующей системе уравнений:
| 2 α 1 + 4 α 2 = 0 |
| 5 α 1 + 10 α 2 = 0 | |
| α 1 + 0 α 2 = 0 |
Из 3-тего уравнения получаем α 1 = 0, подставим это значение в 1-ое и 2-ое уравнения:
| 2·0 + 4 α 2 = 0 | => | | 4 α 2 = 0 | => | | α 2 = 0 |
| 5·0 + 10 α 2 = 0 | 10 α 2 = 0 | α 2 = 0 | |||||
| α 1 = 0 | α 1 = 0 | α 1 = 0 |
Так как линейная комбинация строк равна нулю только когда α 1 = 0 и α 2 = 0, то строки линейно независимые.
Линейная зависимость и независимость строк (столбцов) матрицы
Столбец называется линейной комбинацией столбцов одинаковых размеров, если
Если столбцы в (3.1) имеют вид
то матричному равенству (3.1) соответствуют поэлементные равенства
Аналогично формулируется определение линейной комбинации строк одинаковых размеров.
Здесь и далее символом о обозначается нулевой столбец соответствующих размеров.
1. Один столбец тоже образует систему: при — линейно зависимую, а при линейно независимую.
Пример 3.1. Используя определение, установить линейную зависимость или линейную независимость систем столбцов
2) Столбцы линейно независимы, так как равенство
Свойства линейно зависимых и линейно независимых столбцов матриц
Понятия линейной зависимости и линейной независимости определяются для строк и столбцов одинаково. Поэтому свойства, связанные с этими понятиями, сформулированные для столбцов, разумеется, справедливы и для строк.
1. Если в систему столбцов входит нулевой столбец, то она линейно зависима.
2. Если в системе столбцов имеется два равных столбца, то она линейно зависима.
4. Система из 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC8AAAAQCAMAAACx1dbmAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAiXFYMbEhAcBBoPDQoeAQ0I3cqgAAALZJREFUKM+VktsSwyAIRDWKiFf+/2uLSZvEhkxaXnTGs7KsGvN3UYrwC+ffa3D8zCMlxo+QlyfcNmg7v7A/t7VBux/jzkOe54lJURw8ZrHvop0UdM8P+3axGc89aqQ7XuxbjzybMkEUqPLAIPP6/u0g1OYUHnMpTQs02KLxq/0p0Y1O0al+RvqOCcv51CeZF1UeJBjhacoT6PJehTd9k/R7gdgPul7ei3itcWeYPp/sqv4fRhnzAuOaBpbDogV3AAAAAElFTkSuQmCC» /> столбцов линейно зависима тогда и только тогда, когда хотя бы один из столбцов есть линейная комбинация остальных.
5. Любые столбцы, входящие в линейно независимую систему, образуют линейно независимую подсистему.
6. Система столбцов, содержащая линейно зависимую подсистему, линейно зависима.
Докажем, например, последнее свойство. Так как система столбцов линейно зависима, то существуют числа не все равные 0, что
Пример 3.3. Рассмотреть всевозможные системы, образованные из столбцов
Исследовать каждую систему на линейную зависимость.
Рассмотрим системы, содержащие по два столбца:
– каждая из четырех систем и линейно зависима, так как содержит нулевой столбец (свойство 1);
– система линейно зависима, так как столбцы пропорциональны (свойство 3): ;
– каждая из пяти систем и линейно независима, так как столбцы непропорциональные (см. утверждение примера 3.2).
Рассмотрим системы, содержащие три столбца:
– каждая из шести систем и линейно зависима, так как содержит нулевой столбец (свойство 1);
– системы линейно зависимы, так как содержат линейно зависимую подсистему (свойство 6);
– системы и линейно зависимы, так как последний столбец линейно выражается через остальные (свойство 4): и соответственно.
Наконец, системы из четырех или из пяти столбцов линейно зависимы (по свойству 6).
Ранг матрицы. Метод окаймляющих миноров. Линейная независимость строк (столбцов) матрицы
Пусть в матрице А размеров (m; n) выбраны произвольно k строк и k столбцов (k ≤ min(m; n)). Элементы матрицы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу порядка k, определитель которой называется минором Mkk порядка ky или минором k-го порядка матрицы A.
Рангом матрицы называется максимальный порядок r отличных от нуля миноров матрицы A, а любой минор порядка r, отличный от нуля, — базисным минором. Обозначение: rang A = r. Если rang A = rang B и размеры матриц A и Bсовпадают, то матрицы A и B называются эквивалентными. Обозначение: A
Основными методами вычисления ранга матрицы являются метод окаймляющих миноров и метод элементарных преобразований.
Метод окаймляющих миноров
Суть метода окаймляющих миноров состоит в следующем. Пусть в матрице уже найден минор порядка k, отличный от нуля. Тогда далее рассматриваются лишь те миноры порядка k+1, которые содержат в себе (т. е. окаймляют) минорk-го порядка, отличный от нуля. Если все они равны нулю, то ранг матрицы равен k, в противном случае среди окаймляющих миноров (k+1)-го порядка найдется отличный от нуля и вся процедура повторяется.
Линейная независимость строк (столбцов) матрицы
Понятие ранга матрицы тесно связано с понятием линейной независимости ее строк (столбцов).
называют линейно зависимыми, если найдутся такие числа λ1, λ2, λk, что справедливо равенство:
Строки матрицы A называются линейно независимыми, если вышеприведённое равенство возможно лишь в случае, когда все числа λ1 = λ2 = … = λk = 0
Аналогичным образом определяется линейная зависимость и независимость столбцов матрицы A.
Если какая-либо строка (al) матрицы A (где (al)=(al1, al2,…, aln)) может быть представлена в виде
Аналогичным образом определяется понятие линейной комбинации столбцов. Справедлива следующая теорема о базисном миноре.
Базисные строчки и базисные столбцы линейно независимы. Любая строка (либо столбец) матрицы A является линейной комбинацией базисных строк (столбцов), т. е. строк (столбцов), пересекающих базисный минор. Таким образом, ранг матрицы A: rang A = k равен максимальному числу линейно независимых строк (столбцов) матрицы A.
Т.е. ранг матрицы — это размерность самой большой квадратной матрицы внутри той матрицы, для которой нужно определить ранг, для которой определитель не равен нулю. Если исходная матрица не является квадратной, либо если она квадратная, но её определитель равен нулю, то для квадратных матриц меньшего порядка строки и столбцы выбираются произвольно.
Кроме как через определители, ранг матрицы можно посчитать по числу линейно независимых строк или столбцов матрицы. Он равен количеству линейно независимых строк или столбцов в зависимости от того, чего меньше. Например, если матрица имеет 3 линейно независимых строки и 5 линейно независимых столбцов, то её ранг равняется трём.
Примеры нахождения ранга матрицы
Методом окаймляющих миноров найти ранг матрицы
Р е ш е н и е. Минор второго порядка
окаймляющий минор M2, также отличен от нуля. Однако оба минора четвёртого порядка, окаймляющие M3.
равны нулю. Поэтому ранг матрицы A равен 3, а базисным минором является, например, представленный выше минор M3.
Метод элементарных преобразований основан на том, что элементарные преобразования матрицы не меняют её ранга. Используя эти преобразования, можно привести матрицу к виду, когда все её элементы, кроме a11, a22, …, arr (r ≤min (m, n)), равны нулю. Это, очевидно, означает, что rang A = r. Заметим, что если матрица n-го порядка имеет вид верхней треугольной матрицы, т. е. матрицы, у которой все элементы под главной диагональю равны нулю, то её определитесь равен произведению элементов, стоящих на главной диагонали. Это свойство можно использовать при вычислении ранга матрицы методом элементарных преобразований: необходимо с их помощью привести матрицу к треугольной и тогда, выделив соответствующий определитель, найдём, что ранг матрицы равен числу элементов главной диагонали, отличных от нуля.
Методом элементарных преобразований найти ранг матрицы
Р е ш е н и е. Обозначим i-ю строку матрицы A символом αi. На первом этапе выполним элементарные преобразования
На втором этапе выполним преобразования
В результате получим
На третьем этапе мы переставили четвёртую строку на место третьей, а третью — на место четвёртой. На четвёртом этапе мы разделили элементы четвёртого и пятого столбцов на 4 и 2 и поменяли местами третий и четвёртый столбцы. Из вида матрицы, получившегося после четвёртого этапа преобразования, следует, что rang A = 3. Можно было бы продолжить преобразование матрицы A, добиваясь обнуления остальных элементов матрицы с различными индексами, но вряд ли это целесообразно при нахождении ранга матрицы. Заметим также, что получившуюся в результате элементарных преобразований нулевую строку можно было бы не писать при дальнейших преобразованиях матрицы, а просто вычеркнуть, что, очевидно, никак не повлияет на ранг исходной матрицы.
Как найти ранг матрицы в wxMaxima и Maxima
Для нахождения ранга матрицы используется функция rank: