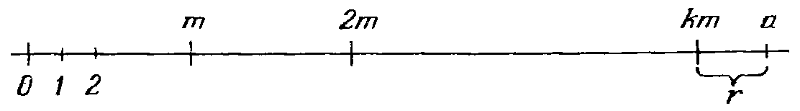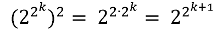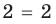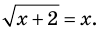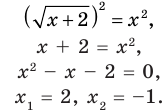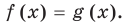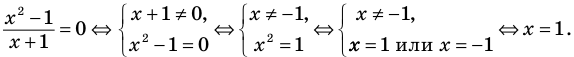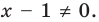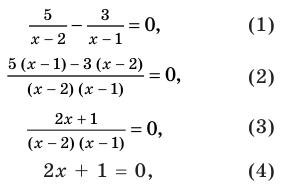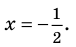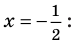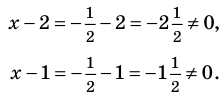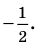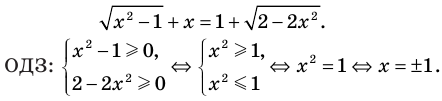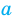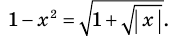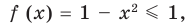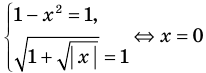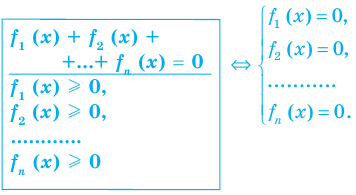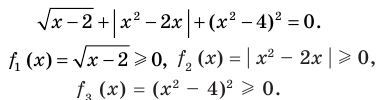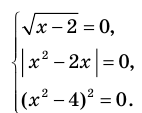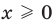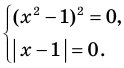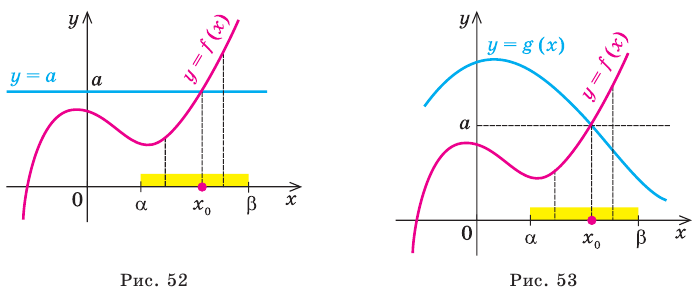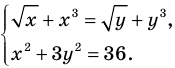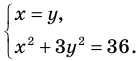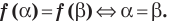Что значит сравнить уравнения
Что такое уравнение и корни уравнения? Как решить уравнение?
Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.
Что такое уравнение? Смысл и понятия.
Узнаем сначала все понятия, связанные с уравнением.
Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.
Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.
Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.
Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.
Рассмотрим теперь, все термины на простом примере:
x+1=3
В данном случае x – переменная или неизвестное значение уравнения.
Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.
Получили верное равенство. Значит, правильно нашли корни уравнения.
Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.
Правила уменьшения или увеличения уравнения на определенное число.
Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7
Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.
Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.
Проверка:
Вместо переменной x подставим 5.
x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.
Разберем следующий пример:
Решите уравнение x-4=12.
Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:
Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16
Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.
Рассмотрим пример:
Решите уравнение 4+3x=2x-5
Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9
Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.
Правила уменьшения или увеличения уравнения в несколько раз.
Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.
Рассмотрим пример:
Решите уравнение 5x=20.
Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.
5x=20
5x :5 =20 :5
5:5x=4
1x=4 или x=4
Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅ 4 =20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.
Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.
Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.
7=7 получено верное равенство.
Ответ: корень уравнения равен x=21.
Следующий пример:
Найдите корни уравнения
Далее делим все уравнение на 3.
Сделаем проверку. Подставим в уравнение найденный корень.
Как решать уравнения? Алгоритм действий.
Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:
Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.
Что значит сравнить уравнения
§ 1. Определение сравнения
Теория чисел имеет свою алгебру, известную, как теория сравнений. Обычная алгебра первоначально развивалась как стенография для операций арифметики. Аналогично, сравнения представляют собой символический язык для делимости, основного понятия теории чисел. Понятие сравнения впервые ввел Гаусс.
Прежде чем мы обратимся к понятию сравнения, сделаем одно замечание о числах, которые будем изучать в этой главе. Мы начали эту книгу, заявив, что будем рассматривать целые положительные числа 1, 2, 3…, и в предыдущих главах мы ограничивались только этими числами и дополнительным числом 0. Но теперь мы достигли стадии, на которой целесообразно расширить наши границы, рассматривая все целые числа:
Это никоим образом не повлияет на наши предыдущие понятия; далее, когда мы будем говорить о простых числах, делителях, наибольших общих делителях и тому подобном, мы будем считать их целыми положительными числами.
Теперь вернемся к языку сравнений. Если а и b — два целых числа и их разность а — b делится на число m, мы выражаем это записью
которая читается так:
а сравнимо с b по модулю m.
Делитель m мы предполагаем положительным; он называется модулем сравнения. Наше высказывание (7.1.1) означает, что
a — b = mk, где k — целое число. (7.1.2)
1) 23 ≡ 8 (mod 5), так как 23 — 8 = 15 = 5 3;
2) 47 ≡ 11 (mod 9), так как 47–11 = 36 = 9 4;
3) —11 ≡ 5 (mod 8), так как — 11 — 5 = —16 = 8 (-2);
4) 81 ≡ 0 (mod 27), так как 81 — 0 = 81 = 27 3.
Последний пример показывает, что вообще, вместо того, чтобы говорить: число а делится на число m, мы можем записать
так как это означает, что
где k — некоторое целое число. Например, вместо того, чтобы сказать, что а — четное число, мы можем записать
Таким же образом видно, что нечетное число является числом, удовлетворяющим сравнению
Эта несколько странная терминология является довольно обычной для математических работ.
§ 2. Некоторые свойства сравнений
Способ, которым мы записываем сравнения, напоминает нам уравнения, и в действительности, сравнения и алгебраические уравнения имеют много общих свойств. Простейшими из них являются три следующих свойства:
это является следствием того, что
Это следует из того, что b — a = — (а — b) = m(—k).
следует, что а ≡ c (mod m), потому что первые два утверждения означают, что
Пример. Из того, что 13 ≡ 35 (mod 11) и 35 ≡ — 9 (mod 11) следует, что 13 ≡ — 9 (mod 11).
Мы говорили, что сравнения похожи по своему свойству на равенства. В действительности, мы можем рассматривать равенства как тип сравнения, а именно, сравнения по модулю 0. По определению,
Вы почти никогда не встретите такую форму сравнения для записи уравнений в математической литературе. Но существует другое сравнение, очевидно, довольно тривиальное, которое иногда используется. Когда модуль есть число m = 1, мы имеем, что
для любой пары целых чисел а и b, так как это означает, что
есть целое число. Но предположим теперь на мгновение, что а и b — произвольные вещественные числа, необязательно целые. Тогда тот факт, что они сравнимы по модулю 1, означает, что их разность есть целое число, т. е. эти два числа имеют одинаковую дробную часть.
Пример. 8 1/3 ≡ 1 1/3 (mod 1), или
Вернемся к свойствам обычных сравнений целых чисел; с этого момента мы будем всегда считать, что модуль является целым числом т ≥ 2.
Мы можем разделить числовую ось, начиная от начала координат в обоих направлениях на отрезки длиной m, как на рис. 17. Тогда каждое целое число а, положительное или отрицательное, попадает на один из этих отрезков или на одну из точек деления; таким образом, мы можем записать
где k — некоторое целое число, а r— одно из чисел
Это является незначительным обобщением деления положительных чисел, описанного в § 3 главы 4. Здесь мы также называем число r в формуле (7.2.6) остатком при делении числа а на число m или остатком по модулю m.
1) а = 11, m = 7, 11 = 7 1 + 4,
2) а = —11, m = 7, —11 = 7 (—2) + 3.
Деление (7.2.6) может быть также записано как сравнение
Таким образом, каждое число сравнимо со своим остатком по модулю m. В приведенных выше примерах мы имеем
11 ≡ 4 (mod 7), — 11 ≡ 3 (mod 7).
Никакие два остатка в (7.2.7) не сравнимы по (mod m), так как разность между любыми двумя из них меньше, чем m. Поэтому два числа, которые не сравнимы по (mod m), должны иметь разные остатки. Итак, мы делаем вывод:
сравнение а ≡ b(mod m) выполняется тогда и только тогда, когда числа а и b имеют одинаковые остатки при делении на число m.
Существует другой способ представления этого сравнения. Предположим на мгновение, что а и b — целые положительные числа. Мы видели при обсуждении системы чисел в § 2 главы 6, что когда число а записано при основании m,
то последняя цифра а0 является остатком числа а при делении его на число m. Если мы используем этот факт, чтобы иначе выразить нашу интерпретацию сравнения, то можно сказать:
сравнение а ≡ b (mod m) выполняется для целых (положительных) чисел а и b тогда и только тогда, когда числа а и b имеют одинаковые последние цифры в записи при основании m.
так как эти два числа имеют одну и ту же последнюю цифру в десятичной системе чисел.
1. Найдите остатки —37(mod 7), — 111 (mod 11), — 365 (mod 30).
§ 3. Алгебра сравнений
Из алгебры мы помним, что уравнения можно складывать, вычитать, умножать. Точно такие же правила справедливы для сравнений. Предположим, что мы имеем сравнения
По определению, это означает, что
где k и l — целые числа. Сложим уравнения (7.3.2).
В результате получаем
что можем записать как
другими словами, два сравнения можно складывать. Таким же образом можно показать, что одно сравнение можно вычитать из другого, т. е. что
11 ≡ —5 (mod 8) и 7 = — 9 (mod 8). (7.3.5)
Складывая их, получаем
Оба эти сравнения справедливы.
Можно также перемножить два сравнения. Из (7.3.1) и (7.3.2) следует, что
Пример. Когда два сравнения из (7.3.5) перемножены, получается
Сравнение a ≡ b (mod m) может быть умножено на любое целое число с, при этом получаем
Это можно рассматривать как частный случай умножения сравнений (7.3.6) при с = d. Его можно также рассматривать как прямое следствие из определения сравнения.
Пример. Когда первое сравнение из (7.3.5) умножается на 3, получаем, что
Возникает естественный вопрос: в каком случае можно в сравнении (7.3.7) сократить общий множитель с и получить при этом верное сравнение
Именно здесь сравнения отличаются от уравнений. Например, верно, что
но сокращение на множитель 2 дало бы сравнение
В одном важном случае сокращение допустимо:
если ас ≡ bc (mod m), то a ≡ b (mod m) при условии, что числа m и с взаимно просты.
Доказательство. Первое сравнение означает, что
Если D(m, с) = 1, то отсюда следует, что а — b делится на m в соответствии с результатом, доказанным в § 2 главы 4.
мы можем сократить на множитель 4, так как D(11, 4) = 1. Это дает
1. Придумайте еще несколько примеров на использование изложенных правил действий со сравнениями.
§ 4. Возведение сравнений в степень
Предположим вновь, что имеется сравнение
Как мы только что видели, можно умножить это сравнение на себя, получив
Вообще можно, умножив это сравнение на себя нужное количество раз, получить
для любого целого положительного числа m.
после возведения в квадрат следует сравнение
а после возведения в куб получаем сравнение
Многие результаты теории сравнений связаны с остатками высоких степеней чисел, поэтому покажем, как можно продолжить процесс возведения в степень. Предположим, например, что мы хотим найти остаток сравнения
Одним из путей для выполнения этого является повторное возведение в квадрат. Мы находим:
89 = 64 + 16 + 8 + 1 = 2 6 + 2 4 + 2 3 + 1,
то отсюда следует, что
3 89 = 3 64 • З 16 • З 8 • 3 = 4 • 4 • 2 • 3 ≡ 5 (mod 7).
В действительности, для того чтобы найти этот остаток, мы записали показатель степени
89 = 2 6 + 2 4 + 2 3 + 1 = (1, 0, 1, 1, 0, 0, 1)
в двоичной системе счисления. Повторным возведением в квадрат мы нашли остатки (по модулю 7) тех степеней числа 89, которые сами являются степенями числа 2:
Соответствующий метод можно использовать для любых других оснований. Однако в частном случае бывает возможность упростить вычисление, если заметить особенности этого случая. Например, в случае, разобранном выше, мы можем отметить, что
откуда заключаем, что
3 84 = (3 6 ) 14 ≡ 1 (mod7).
В качестве другой иллюстрации сказанного можно рассмотреть числа Ферма, с которыми мы познакомились в § 3 гл. 2:
Первые пять чисел Ферма таковы:
Отсюда можно высказать предположение:
десятичная запись всех чисел Ферма, за исключением F0 и F1 оканчивается цифрой 7.
Докажем с помощью сравнений, что это действительно так. Очевидно, что оно равносильно утверждению, что числа
оканчиваются цифрой 6. Это можно доказать по индукции. Заметим, что
2 2³ = 256 ≡ 6 (mod 10),
2 2ˆ4 = 65536 ≡ 6 (mod 10),
Предположим, что для некоторого значения t
возводя в квадрат это сравнение, мы находим, что
Из алгебры мы знаем правила возведения бинома в степень:
Здесь первый и последний коэффициенты равны единице. Средними биномиальными коэффициентами являются
Так как эти коэффициенты получаются в результате последовательного умножения на бином (х + у), то ясно, что они являются целыми числами.
С этого момента будем считать, что р — простое число. Чтобы записать эти коэффициенты в целочисленном виде, необходимо сократить все общие множители знаменателя
Однако знаменатель не содержит простого множителя р, поэтому после сокращения число р останется множителем в числителе. Мы делаем вывод.
Все биномиальные коэффициенты (кроме первого и последнего) в выражении (7.5.2) делятся на р, если р — простое число.
Пусть теперь х и у в выражении (7.5.2) будут целыми числами. Если мы рассмотрим формулу (7.5.2) как сравнение по модулю р, то можно сделать вывод, что для любых целых чисел х и у и простого р
В качестве примера возьмем р = 5:
Так как все средние коэффициенты делятся на 5, то
в соответствии с (7.5.5).
Из сравнения (7.5.5) можно сделать важные выводы. Применим его для случая х = у = 1. Получаем
Возьмем затем х = 2, у = 1 и найдем, что
теперь, используя предыдущий результат, 2 p ≡ 2 (mod p), получаем
Итак, 3 p ≡ 3 (mod p). Далее для х = 3, у = 1 получаем
Используя этот процесс, можно доказать по индукции, что а p ≡ a (mod p) для всех значений числа
Случаи a = 0 и а = 1 очевидны. Так как каждое число сравнимо (mod р) с одним из остатков, записанных в (7.5.6), мы делаем вывод:
для любого целого числа а и любого простого числа р
Это утверждение обычно называют теоремой Ферма, хотя некоторые авторы называют ее малой теоремой Ферма, чтобы отличить от последней теоремы Ферма, или гипотезы Ферма, о которой мы упоминали в § 3 главы 5.
2 13 = 2 8 • 2 4 • 2 ≡ 9 • 3 • 2 ≡ 2 (mod 13),
как и утверждает теорема Ферма.
В соответствии с правилом сокращения для сравнений, сформулированном в конце § 3, мы можем сократить общий множитель а в обеих частях записи теоремы Ферма (7.5.7) при условии, что число а взаимно просто с числом р, являющимся модулем сравнения. Это дает следующий результат:
если а является целым числом, не делящимся на простое число р, то
Этот результат также называют теоремой Ферма.
Пример. Когда а = 7, р = 19, мы находим, что
7 2 = 49 ≡ 11 (mod 19)
7 4 ≡ 121 ≡ 7 (mod 19),
7 8 ≡ 49 ≡ 11 (mod 19),
7 16 ≡ 121 ≡ 7 (mod 19),
что соответствует утверждению (7.5.8).
В качестве приложения теоремы Ферма вновь рассмотрим треугольники Пифагора, обсужденные в гл. 5 и докажем следующее утверждение:
произведение длин сторон треугольника Пифагора делится на 60.
Доказательство. Очевидно, достаточно доказать это для простейших треугольников. В соответствии с формулой (5.2.7), это произведение есть
Число Р делится на 60 тогда и только тогда, когда оно делится на 4, на 3 и на 5. Так как одно из чисел m и n четно, то 2mn, а следовательно, и число Р, делится на 4. Оно делится на 3, если хотя бы одно из чисел m или n делится на 3, но если ни одно из них не делится на 3, то Р все же будет делиться на 3, так как из условий (7.5.8), а также D(m, 3) = 1 и D (n, 3) = 1 следует, что m 2 ≡ 1 (mod 3) и n 2 ≡ 1 (mod 3), так что
m 2 — n 2 ≡ 1 – 1 = 0 (mod 3).
Аналогично, число Р делится на 5. Это очевидно, если m или n делится на 5. Если ни одно из них не делится на 5, то вновь по теореме Ферма (7.5.8) получаем
m 4 — n 4 ≡ 1 – 1 = 0 (mod 5).
Содержание:
Уравнения
Уравнения-следствия и равносильные преобразования уравнений
1. Понятие уравнения и его корней
Определение:
Равенство с переменной называется уравнением. В общем виде уравнение с одной переменной
Под этой краткой записью понимают математическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны
Пример:
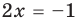
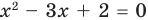
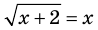
Корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство.
Решить уравнение — значит найти все его корни или доказать, что их нет
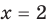
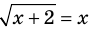
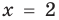
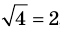
2. Область допустимых значений (ОДЗ)
Областью допустимых значений (или областью определения) уравнения называется общая область определения для функций 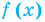
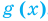
Для уравнения 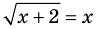
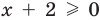
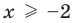
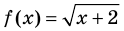

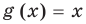
3. Уравнения-следствия
Если каждый корень первого уравнения является корнем второго, то второе уравнение называется следствием первого уравнения.
Если из правильности первого равенства следует правильность каждого последующего, то получаем уравнения-следствия.
При использовании уравнений-следствий не происходит потери корней исходного уравнения, но возможно появление посторонних корней. Поэтому при использовании уравнений-следствий проверка полученных корней подстановкой их в исходное уравнение является составной частью решения.
Пример:
Решение:
► Возведем обе части уравнения в квадрат:
Проверка, 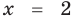
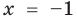
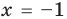
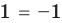
4. Равносильные уравнения
Определение:
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни.
То есть каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого. (Схема решения уравнений с помощью равносильных преобразований приведена в пункте 5 этой таблицы)
Простейшие теоремы
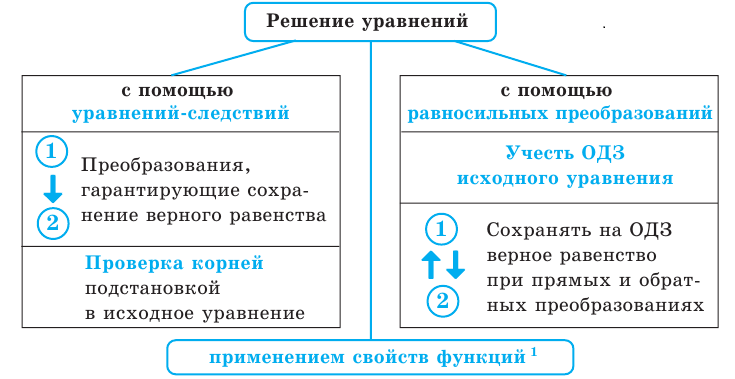
5. Схема поиска плана решения уравнений



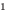
Объяснение и обоснование:
Понятие уравнения и его корней
Уравнение в математике чаще всего понимают как аналитическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны. Поэтому в общем виде уравнения с одной переменной 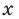
Часто уравнения определяют короче — как равенство с переменной.
Напомним, что корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство. Решить уравнение — значит найти все его корни или доказать, что их нет.
Например, уравнение 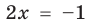
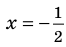
а уравнение 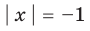
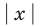
Область допустимых значений (ОДЗ) уравнения
Если задано уравнение 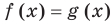
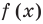
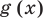
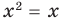
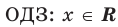
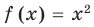
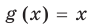
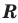
Понятно, что каждый корень данного уравнения принадлежит как области определения функции 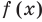
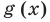
Например, в уравнении 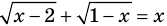
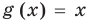
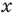
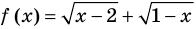
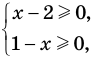
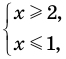
Заметим, что нахождение ОДЗ данного уравнения может быть полезным для его решения, но не всегда является обязательным элементом решения уравнения.
Методы решения уравнений
Для решения уравнений используют методы точного и приближенного решений. А именно, для точного решения уравнений в курсе математики 5-6 классов использовались зависимости между компонентами и результатами действий и свойства числовых равенств; в курсе алгебры 7-9 классов — равносильные преобразования уравнений, а для приближенного решения уравнений — графический метод.
Графический метод решения уравнений не дает высокой точности нахождения корней уравнения, и с его помощью чаще всего можно получить только грубые приближения корней. Иногда удобно графически определить количество корней уравнения или найти границы, в которых находятся эти корни. В некоторых случаях можно графически доказать, что уравнение не имеет корней. По указанным причинам в школьном курсе алгебры и начал анализа под требованием «решить уравнение» понимается требование «используя методы точного решения, найти корни данного уравнения». Приближенными методами решения уравнений можно пользоваться только тогда, когда об этом говорится в условии задачи (например, если ставится задача решить уравнение графически).
В основном при решении уравнений разных видов нам придется применять один из двух методов решения. Первый из них состоит в том, что данное уравнение заменяется более простым уравнением, имеющим те же корни,— равносильным уравнением. В свою очередь, полученное уравнение заменяется еще более простым, равносильным ему, и т. д. В результате получаем простейшее уравнение, которое равносильно заданному и корни которого легко находятся. Эти корни и только они являются корнями данного уравнения.
Второй метод решения уравнений состоит в том, что данное уравнение заменяется более простым уравнением, среди корней которого находятся все корни данного, то есть так называемым уравнением-следствием. В свою очередь, полученное уравнение заменяется еще более простым уравнением-следствием, и так далее до тех пор, пока не получим простейшее уравнение, корни которого легко находятся. Тогда все корни данного уравнения находятся среди корней последнего уравнения. Поэтому, чтобы найти корни данного уравнения, достаточно корни последнего уравнения подставить в данное и с помощью такой проверки получить корни данного уравнения (и исключить так называемые посторонние корни — те корни последнего уравнения, которые не удовлетворяют заданному).
В следующем пункте будет также показано применение свойств функций к решению уравнений определенного вида.
Уравнения-следствия
Рассмотрим более детально, как можно решать уравнения с помощью уравнений-следствий. При решении уравнений главное — не потерять корни данного уравнения, и поэтому в первую очередь мы должны следить за тем, чтобы каждый корень исходного уравнения оставался корнем следующего. Фактически это и является определением уравнения-следствия:
в том случае, когда каждый корень первого уравнения является корнем второго, второе уравнение называется следствием первого.
Это определение позволяет обосновать такой ориентир: для получения уравнения-следствия достаточно рассмотреть данное уравнение как верное числовое равенство и гарантировать (то есть иметь возможность обосновать), что каждое следующее уравнение мы можем получить как верное числовое равенство.
Действительно, если придерживаться этого ориентира, то каждый корень первого уравнения обращает это уравнение в верное числовое равенство, но тогда и второе уравнение будет верным числовым равенством, то есть рассматриваемое значение переменной является корнем и второго уравнения, а это и означает, что второе уравнение является следствием первого.
Применим приведенный ориентир к уравнению 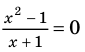
Если правильно то, что дробь равна нулю, то обязательно ее числитель равен нулю. Таким образом, из заданного уравнения получаем уравнение-следствие 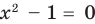
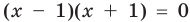
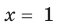
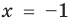
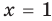
Это происходит поэтому, что, используя уравнения-следствия, мы гарантируем только то, что корни заданного уравнения не теряются (каждый корень первого уравнения является корнем второго). Но второе уравнение, кроме корней первого уравнения, имеет еще и другой корень, который не является корнем первого уравнения. Для первого уравнения этот корень является посторонним, и, чтобы его отсеять, выполняется проверка подстановкой корней в исходное уравнение. (Более полно причины появления посторонних корней рассмотрены в таблице 9.) Таким образом, чтобы правильно применять уравнения-следствия для решения уравнений, необходимо помнить еще один ориентир: при использовании уравнений-следствий возможно появление посторонних корней, и поэтому проверка подстановкой корней в исходное уравнение является составной частью решения.
Схема применения этих ориентиров дана в таблице 8. В пункте 3 этой таблицы приведено решение уравнения
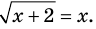
Для решения этого уравнения с помощью уравнений-следствий достаточно данное уравнение рассмотреть как верное числовое равенство и учесть, что в случае когда два числа равны, то и их квадраты также будут равны:
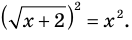
То есть мы гарантируем, что если равенство (1) верно, то и равенство (2) также будет верным, а это и означает (как было показано выше), что уравнение (2) является следствием уравнения (1). Если мы хотя бы один раз использовали уравнения-следствия (а не равносильные преобразования), то можем получить посторонние корни, и тогда в решение обязательно входит проверка полученных корней подстановкой их в заданное уравнение.
Замечание. Переход от данного уравнения к уравнению-следствию можно обозначить специальным значком 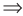
Равносильные уравнения
С понятием равносильности вы знакомы еще из курса алгебры 7 класса, где равносильными назывались те уравнения, которые имели одни и те же корни. Заметим, что равносильными считались и такие два уравнения, которые не имели корней. Формально будем считать, что и в этом случае уравнения имеют одни и те же корни, поскольку ответы к таким уравнениям одинаковы: «уравнения не имеют корней» (точнее: одинаковыми являются множества корней таких уравнений — они оба пустые, что обозначается символом 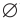
В курсе алгебры и начал анализа мы будем рассматривать более общее понятие равносильности, а именно: равносильность на определенном множестве.
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни, то есть каждый корень первого уравнения является корнем второго и, наоборот, каждый корень второго уравнения является корнем первого.
Для уравнений, заданных на множестве всех действительных чисел (например, для линейных), мы можем однозначно дать ответ на вопрос: «Равносильны ли данные уравнения?» Например, уравнения 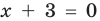
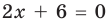
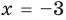
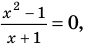
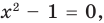
то, как было показано выше, уравнение (3) имеет единственный корень 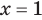
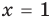
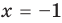
всех действительных чисел эти уравнения не являются равносильными, поскольку у уравнения (4) есть корень 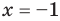
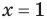
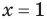
Укажем, что множество, на котором рассматривается равносильность уравнений, как правило, не задается искусственно (как в последнем случае), а чаще всего таким множеством является ОДЗ исходного уравнения. Договоримся, что далее
все равносильные преобразования уравнений (а также неравенств и систем уравнений и неравенств) мы будем выполнять на ОДЗ исходного уравнения (неравенства или системы).
Отметим, что в том случае, когда ОДЗ заданного уравнения является множество всех действительных чисел, мы не всегда будем ее записывать (как не записывали ОДЗ при решении линейных или квадратных уравнений). И в других случаях главное — не записать ОДЗ в решение уравнения, а реально учесть ее при выполнении равносильных преобразований данного уравнения.
Например, для уравнения 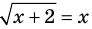
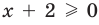

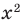
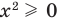
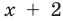


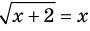
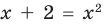
Для выполнения равносильных преобразований попробуем выделить общие ориентиры, аналогичные соответствующим ориентирам получения уравнений-следствий. Как указывалось выше, выполняя равносильные преобразования уравнений, необходимо учесть ОДЗ данного уравнения — это и есть первый ориентир для выполнения равносильных преобразований уравнений. По определению равносильности уравнений необходимо гарантировать, чтобы каждый корень первого уравнения был корнем второго и, наоборот, каждый корень второго уравнения был корнем первого. Для первой части этого требования мы уже выделили общий ориентир: достаточно гарантировать сохранение правильности равенства при переходе от первого уравнения ко второму.
Но тогда, чтобы выполнить вторую часть этого требования, достаточно второе уравнение рассмотреть как верное равенство (то есть взять такое значение переменной, которое является корнем второго уравнения) и гарантировать, что при переходе к первому верное равенство сохраняется (этот корень остается и корнем первого уравнения). Фактически из определения равносильности уравнений получаем, что каждое из равносильных уравнений является следствием другого уравнения). Таким образом, при выполнении равносильных преобразований мы должны гарантировать сохранение правильности равенства на каждом шаге решения не только при прямых, но и при обратных преобразованиях — это и является вторым ориентиром для решения уравнений с помощью равносильных преобразований. (Соответствующие ориентиры схематически представлены в пункте 5 табл. 8.)
Например, чтобы решить с помощью равносильных преобразований уравнение 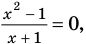
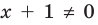
Запись решения в этом случае может быть такой:
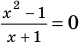
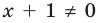
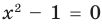
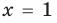
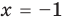
Для выполнения равносильных преобразований уравнений можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности уравнений обобщим также формулировки простейших теорем о равносильности, известных из курса алгебры 7 класса.
Теорема 1. Если из одной части уравнения перенести в другую часть слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве).
Теорема 2. Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получаем уравнение, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований данного уравнения.
Замечание. Для обозначения перехода от данного уравнения к равносильному ему уравнению можно применять специальный значок 
Пример №423
Решите уравнение 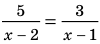
Решение:
► ОДЗ: 
На этой ОДЗ данное уравнение равносильно уравнениям:
то есть
Учтем ОДЗ. При
Таким образом, 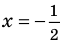
Ответ:
Используем равносильные преобразования для решения данного уравнения. Для этого необходимо учесть ОДЗ, поэтому зафиксируем ее ограничения в начале решения.
Укажем, что в уравнениях ограничения ОДЗ можно только зафиксировать, но не решать, а в конце проверить, выполняются ли эти ограничения для найденных корней.
При переносе члена данного уравнения из одной части уравнения в другую с противоположным знаком получаем уравнение (1), равносильное заданному.
Приводя к общему знаменателю, раскрывая скобки и приводя подобные члены, снова получаем верное равенство и можем обосновать, что при выполнении обратных действий равенство также не нарушается, таким образом, полученные уравнения (1)-(3) равносильны заданному (на его ОДЗ).
Дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю. Но второе условие уже учтено в ограничениях ОДЗ, таким образом, получаем уравнение (4), равносильное заданному уравнению на его ОДЗ. Поскольку все преобразования были равносильными только с учетом ОДЗ, то мы должны проверить, удовлетворяет ли полученное число ограничениям ОДЗ.
Причины появления посторонних корней и потери корней при решении уравнений
Наиболее типичные случаи появления посторонних корней и потери корней приведены в таблице 9. Там же указано, как в каждом из этих случаев получить правильное (или полное) решение.
Применение свойств функций к решению уравнений
1. Конечная ОДЗ
Если область допустимых значений (ОДЗ) уравнения (неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения
Пример:
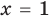
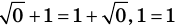
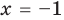
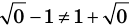
2. Оценка левой и правой частей уравнения
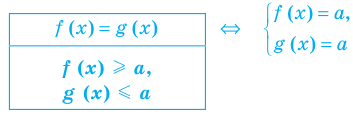
Если надо решить уравнение вида 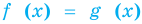


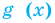
Пример:
►
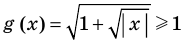
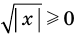
Итак, заданное уравнение равносильно системе
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю
Пример:
►
Итак, заданное уравнение равносильно системе
Из первого уравнения получаем 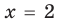
3. Использование возрастания и убывания функций
Схема решения уравнения
1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет (используя теоремы о корнях уравнения или оценку левой и правой частей уравнения)
Теоремы о корнях уравнения
Если в уравнении 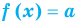
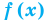
Пример:
Уравнение 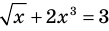
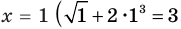
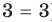
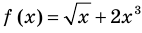
Если в уравнении 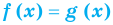
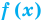
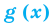
Пример:
Уравнение 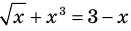
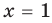
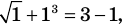
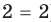
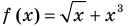

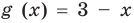
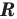
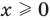
Объяснение и обоснование:
Конечная ОДЗ
Напомним, что в случае, когда дано уравнение 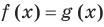
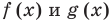
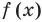
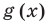
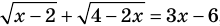
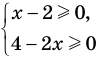
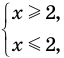


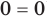


Рассмотренный пример позволяет выделить ориентир для решения аналогичных уравнений:
если ОДЗ уравнения (а также неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения.
Замечание. В том случае, когда ОДЗ — пустое множество (не содержит ни одного числа), мы можем сразу дать ответ, что данное уравнение не имеет корней.
Например, если необходимо решить уравнение 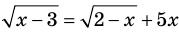
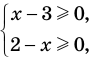
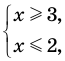
Оценка левой и правой частей уравнения
Некоторые уравнения можно решить с помощью оценки левой и правой частей уравнения.
Пусть дано уравнение 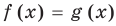
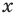
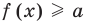
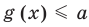
Рассмотрим два случая:
Если 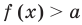
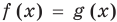
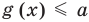
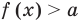
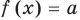
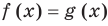
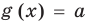
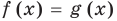
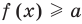
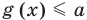
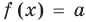
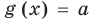
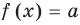
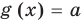
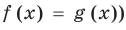
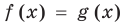
Коротко это можно записать так:
Пример использования такого приема решения уравнений приведен в пункте 2 таблицы 10.
Аналогично предыдущим рассуждениям обосновывается и ориентир по решению уравнения 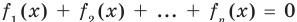
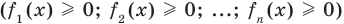
Если предположить, что 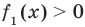

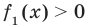
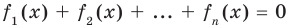
Например, чтобы решить уравнение 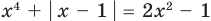
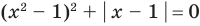
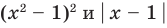
Из второго уравнения получаем 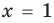
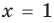
Использование возрастания и убывания функций к решению уравнений
Использование возрастания и убывания функций к решению уравнений опирается на такое свойство: возрастающая или убывающая функция принимает каждое свое значение только в одной точке ее области определения.
Полезно помнить специальные теоремы о корнях уравнения.
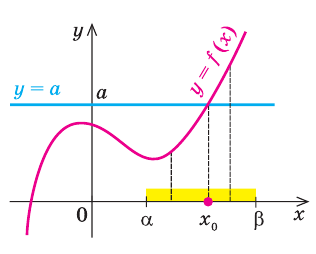
Теорема 1. Если в уравнении 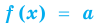
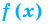
Графически утверждение теоремы проиллюстрировано на рисунке 52. Прямая 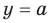
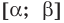
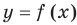
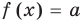
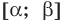
• Если на промежутке 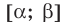
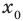
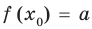
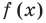
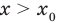
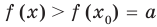
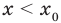
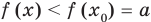
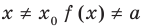
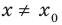
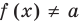
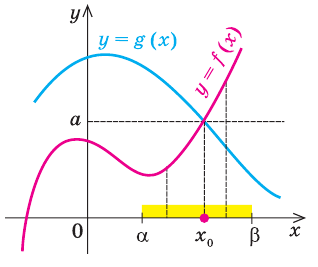
Теорема 2. Если в уравнении 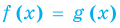
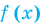
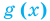
Графически утверждение теоремы проиллюстрировано на рисунке 53.
• Если на промежутке 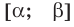
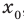
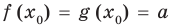
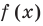
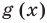
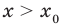
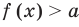
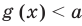
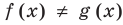
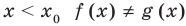
Каждая из этих теорем утверждает, что в рассмотренном промежутке данное уравнение может иметь не более чем один корень, то есть или это уравнение совсем не имеет корней, или оно имеет единственный корень. Если нам удалось подобрать один корень такого уравнения, то других корней в заданном промежутке уравнение не имеет.
Например, чтобы решить уравнение 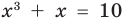
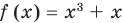

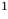
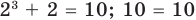
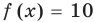
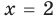
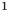

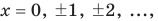
Заметим, что каждая из этих теорем гарантирует единственность корня уравнения (если он есть) только на промежутке возрастания (или убывания) соответствующей функции. Если функция имеет несколько промежутков возрастания и убывания, то приходится рассматривать каждый из них отдельно.
Пример:
Решим с помощью теоремы 2 уравнение 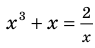
► Сначала следует учесть его ОДЗ: 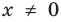
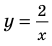
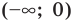
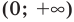
1) При 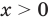
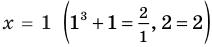
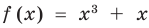

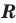
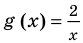

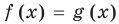
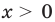
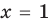
Примеры решения задач:
Пример №424
Решите уравнение 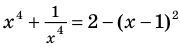
Решение:
► ОДЗ: 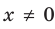
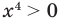
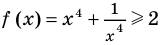
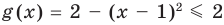
Таким образом, данное уравнение равносильно системе 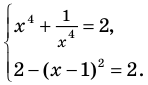


Если раскрыть скобки и привести обе части уравнения к общему знаменателю, то для нахождения корней полученного уравнения придется решать полное уравнение восьмой степени, все корни которого мы не сможем найти.
Попытаемся оценить области значений функций, стоящих в левой и правой частях уравнения. Поскольку на ОДЗ 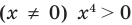
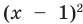
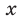
Пример №425
Решите систему уравнений
Решение:
► ОДЗ: 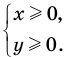
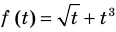
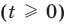
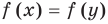
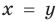
Подставляя 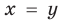
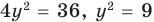
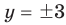

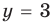
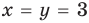
Иногда свойства функций удается применить при решении систем уравнений. Если заметить, что в левой и правой частях первого уравнения заданной системы стоят значения одной и той же функции, которая является возрастающей (как сумма двух возрастающих функций), то равенство 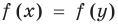
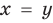
Замечание. Утверждение, обоснованное в комментарии к задаче 2, может быть использовано при решении аналогичных задач. Коротко его можно сформулировать так: если функция 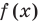
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.