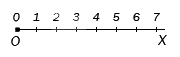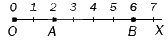Что значит сравнить два различных натуральных
ВОПРОСЫ
1. Что значит сравнить два различных натуральных числа?
2. Как, используя натуральный ряд, можно определить, какое из двух натуральных чисел меньше? Больше?
3. Какое число меньше любого натурального числа?
Число 0 меньше любого натурального числа.
4. Как сравнивать натуральные числа, имеющие разное количество цифр?
Из двух натуральных чисел, имеющих разное количество цифр, большим является то, у которого количество цифр больше.
5. Какое из натуральных чисел с одинаковым количеством цифр больше?
Из двух натуральных чисел, имеющих одинаковое количество цифр, большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр.
6. Как на координатном луче расположена точка с меньшей координатой относительно точки с большей координатой?
На координатном луче точка с меньшей координатой расположена левее точки с большей координатой.
РЕШАЕМ УСТНО
1. Какое из чисел 516 и 615 расположено на координатном луче левее?
Число 516 расположено на координатном луче левее, чем число 615.
2. Какое из чисел 405 и 504 расположено на координатном луче правее?
Число 504 расположено на координатном луче правее, чем 405.
Цена деления термометра равна 2°С.
4. Вычислите:
5. В коробке лежат пять красных и три зеленых карандаша. Наугад из нее вынимают по одному карандашу. Какое наименьшее количество карандашей над взять, чтобы среди них были хотя бы два красных и один зеленый?
УПРАЖНЕНИЯ
142. Прочитайте неравенство:
143. Запишите в виде неравенства утверждение:
144. Сравните числа:
145. Сравните числа:
146. Расположите в порядке возрастания числа: 894, 479, 846, 591, 701.
479, 591, 701, 846, 894.
147. Расположите в порядке убывания числа: 639, 724, 731, 658, 693.
731, 724, 693, 658, 639.
148. Назовите все натуральные числа, которые: 1) больше 678, но меньше 684; 2) больше 935, но меньше 940; 3) больше 2 934 450, но меньше 2 934 454; 4) больше 12 706, но меньше 12 708; 5) больше 24 315, но меньше 24 316.
149. Запишите все натуральные числа, которые: 1) больше 549, но меньше 556; 2) больше 1 823 236, но меньше 1 823 240; 3) больше 47 246, но меньше 47 248.
150. Отметьте на координатном луче все натуральные числа которые: 1) меньше 12; 2) больше 4, но меньше 10.
151. Запишите цифру, которую можно поставить вместо звездочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи):
152. Запишите цифру, которую можно поставить вместо звездочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи):
153. 1) Запишите какое-либо натуральное число, которое больше 473 и меньше 664, содержащее цифру 5 в разряде десятков. Сколько таких чисел можно написать?
2) Запишите какое-либо натуральное число, которое больше 578, но меньше 638, содержащее цифру 6 в разряде сотен. Сколько таких чисел можно написать? запишите наименьшее и наибольшее из таких чисел.
154. Запишите какое-либо натуральное число, которое больше 2 364 и меньше 2 432, содержащее цифру 8 в разряде единиц. Сколько таких чисел можно написать? Запишите наименьшее и наибольшее из таких чисел.
157. Запишите в виде двойного неравенства утверждение: 1) число 7 больше 5 и меньше10; 2) число 62 меньше 0 и больше 60; 3) число 54 меньше 94 и больше 44; 4) число 128 больше 127 и меньше 129.
158. Запишите в виде двойного неравенства утверждения: 1) число 56 больше 52 и меньше 58; 2) число 258 больше 250 и меньше 261; 3) число 4 325 меньше 4 400 и больше 4 300; 4) число 999 999 меньше 1 000 000 и больше 555 558.
159. В записи чисел вместо нескольких цифр поставили звездочки. Сравните эти числа:
160. В записи чисел вместо нескольких цифр поставили звездочки. Сравните эти числа:
161. Сравните: 1) 2 км и 1 968 м; 2) 4 дм и 4 м; 3) 3 км 94 м и 3 126 м; 4) 712 кг и 8 ц; 5) 15 т и 35 ц; 6) 6 ц 23 кг и 658 кг; 7) 4 т 275 кг и 42 ц 75 кг; 8) 5 т 7 ц 36 кг и 5 т 863 кг; 9) 8 т и 81 ц; 10) 83 дм 7 см и 8 м 30 см.
162. Сравните: 1) 6 892 м и 7 км; 2) 8 см и 8 дм; 3) 4 км 43 м и 4 210 м; 4) 27 дм 3 см и 270 см; 5) 9 ц и 892 кг; 6) 2 ц 86 кг и 264 кг; 7) 3 т 248 кг и 32 ц 84 кг; 8) 12 т 2 кг и 120 ц 2 кг.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
163. Вычислите:
164. Из 24 м ткани можно сшить семь одинаковых платьев. Сколько таких платьев можно сшить из 48 м этой ткани?
165. Знаменитый университет Сорбонна, находящийся в Париже (Франция), основан в 1215 г. Он основан на 6 лет позже Кембриджского университета (Великобритания) и на 540 лет раньше Московского государственного университета имени М.В. Ломоносова. Определите год основания: 1) Кембриджского университета; 2) Московского государственного университета имени М.В. Ломоносова. Сколько лет исполняется в этом году Новосибирскому государственному университету, если Кембриджский университет основан раньше него на 750 лет?
ЗАДАЧА ОТ МУДРОЙ СОВЫ
166. Семь гномов собрали вместе 28 грибов. Все они собрали разное количество грибов, и ни у кого не оказалось пустой корзинки. Сколько грибов собрал каждый гном?
Сравнение натуральных чисел
Вам уже известно, что натуральные числа используются для обозначения количества тех или иных предметов. Возьмем, к примеру, конфеты. Мама купила шоколадные батончики и высыпала их кучкой на столе. Дети пересчитали, и их оказалось 25 штук.
Пришел с работы папа и высыпает рядом еще конфеты. На первый взгляд, эта кучка не отличается от первой, но пересчитав количество папиных конфет, дети увидели, что их всего 23. Значит, эти кучки разные. Чтобы это выяснить, дети произвели два действия:
Сравнить натуральные числа – это означает узнать, отличаются ли они друг от друга или они одинаковые. Если сравниваемые числа отличаются, тогда мы может узнать, что одно число больше другого, а второе, соответственно, меньше первого.
Как сравнить натуральные числа
Сравнить натуральные числа можно такими способами:
В результате сравнения мы можем получить:
Равенство натуральных чисел
Если два натуральных числа имеют полностью одинаковую запись, то и записанные с их помощью числа одинаковы (говорят просто – они равны). Если их записи отличаются, тогда эти числа не равны.
Если мы определили, что числа не равны, тогда нам необходимо выяснить, какое положение они занимают по отношению друг к другу, большее или меньшее.
Запись и чтение неравенств
Неравенство – это запись чисел или математических выражений, которая содержит знаки неравенства.
Читается подобная запись следующим образом. Первое число называется в именительном падеже (кто? что?), а второе в родительном (кого? чего?). Например, так: «два меньше четырех», «восемьдесят девять больше семидесяти восьми».
Если стрелка смотрит влево: « меньше » и означает, что слева от него находится число меньшее, чем справа.
Если стрелка смотрит вправо: «>», такой знак называется « больше » и означает, что слева от него находится большее число, чем справа.
Стрелка знака всегда указывает на меньшее число, а двойная вилка – на большее!
Например, дано неравенство 5 верным (правильно отмеченным), например, 1 неверным (неправильно отмеченным), например, 5>6.
Сравнение однозначных натуральных чисел с помощью ряда
Этот способ лучше всего подходит для сравнения однозначных натуральных чисел.
Меньшим называют число, которое в натуральном ряду находится раньше другого, а большим – то, которое расположено позже другого.
Например, число 2 в натуральном ряду стоит раньше, чем число 4, значит, 2 8.
Число 1 (единица) – самое меньшее из натуральных чисел, поскольку стоит в натуральном ряду первым.
На координатном луче меньшее число обозначается раньше (левее), а большее число – позже (правее) другого числа.
Рис. 1. Большее и меньшее число на координатном луче.
Действительно, чем больше в числе цифр, тем выше разряд самой первой цифры в этом числе.
К примеру, 123456>12345, потому что в первом числе цифра 1 обозначает сотню тысяч, а во втором – десяток тысяч.
Поэтому, для решения задач на сравнение чисел с разным количеством цифр, из которых они состоят, нам достаточно сравнить эти количества:
123456 – шестизначное число, 6 цифр;
12345 – пятизначное число, 5 цифр;
Например, сравним два числа: 12336 и 12345. Оба числа пятизначные. Значит, сравниваем каждую цифру, начиная с 5 разряда (десятков тысяч):
Сравнение двух, трех, и более чисел
Сравнивать между собой можно не только два натуральных числа.
Вернемся к примеру с конфетами на столе. Бабушка тоже купила конфеты и высыпала их на столе. Дети пересчитали их, и в бабушкиной кучке оказалось 33 штуки. Количество конфет мы можем записать натуральными числами: 25, 23 и 33.
Сравнив их между собой, мы увидим три неравенства:
Гораздо удобнее записать результат сравнения в виде двойного неравенства :
23
Как видите, все неравенства верны.
Чтобы быстро записать двойное, тройное, и т.д. неравенство, нужно расставить данные числа слева направо в порядке возрастания (предварительно сравнив между собой), оставив небольшие промежутки между ними. А после этого в оставленные промежутки записать знаки
Сравнение натуральных чисел: равно или не равно, больше или меньше?
Сравнение натуральных чисел между собой – тема данной статьи. Разберем сравнение двух натуральных чисел и изучим понятие равных и неравных натуральных чисел. Выясним большие и меньшие из двух чисел на примерах. Поговорим о натуральном ряде чисел и об их сравнении. Будут показаны результаты сравнений трех и более чисел.
Сравнение натуральных чисел
Рассмотрим это на примере. Когда на дереве имеется стая, состоящая из 7 птиц, а на другом из 5 десятка птиц, то стаи считаются разными, так как не похожи друг на друга. Отсюда можно делать вывод о том, что эта непохожесть и есть сравнение.
При сравнении натуральных чисел проводится такая проверка на похожесть.
Если считать, что под сравнением натуральных чисел подразумевают действие, то оно может привести к нескольким результатам:
Когда получаем неравенство, это значит, что одно из этих чисел больше или меньше другого, что и увеличивает диапазон использования натуральных чисел.
Рассмотрим определения равных и неравных чисел. Разберем, каким образом это определяется.
Равные и неравные натуральные числа
Рассмотрим определение равных и неравных чисел.
В случае, когда записи двух натуральных чисел одинаковы, их считают равными между собой. Когда записи имеют различия, тогда эти числа неравные.
Сравнение однозначных натуральных чисел
Если в записи имеются два натуральных числа со знаками « » и « > », тогда она называется неравенством. Неравенства могут быть верными и неверными.
Запись 4 7 – верная, а 3 > 9 – неверная.
Сравнение однозначного и многозначного натуральных чисел
Если принять за правило, что все однозначные числа меньше двухзначных, тогда получим:
Рассмотрим сравнения многозначных чисел.
Сравнение многозначных натуральных чисел
Рассмотрим сравнение двух неравных многозначных натуральных чисел с равным количеством знаков. Предварительно следует повторить раздел, изучающий разряды натурального числа и значение разряда.
В таком случае производится поразрядное сравнение, то есть слева направо. Меньшим считается число, которое имеет меньшее значение соответствующего разряда и наоборот.
Чтобы решить пример, нужно уяснить, что 0 всегда меньше любого натурального числа и что он равен самому себе. Число ноль относится к разряду натуральных чисел.
Сравнение многозначных натуральных чисел производится по-другому. Большим числом считают то, которое имеет меньшее количество знаков и наоборот.
Решение
Натуральный ряд чисел, нумерация, счет
Эта запись продолжается до бесконечности. Такая бесконечная последовательность чисел называется натуральным рядом чисел.
Существует еще один процесс – счет. Во время счета числа называются одно за другим, то есть таким образом, как они зафиксированы по ряду. Данный процесс применим для определения количества предметов.
Исли имеется определенное число предметов, но нам необходимо узнать количество, используем счет. Он производится, начиная с единицы. Если во время пересчета перекладывать предметы в кучу, то ее можно назвать натуральным рядом чисел. Последний предмет будет являться числом их количества. Когда процесс закончен, мы знаем их число, то есть предметы пересчитаны.
Во время счета меньше то натурально число, которое находится раньше и называется раньше. Применение нумерации используется для конкретного определения предмета, то есть присваивая ему определенный номер. Например, имеем некоторое количество предметов. На каждом из них зафиксируем их порядковый номер. Таким образом производится нумерация. Она применима для различения одинаковых предметов.
Натуральные числа на координатном луче
Для начала необходимо повторить определение координатного луча.
При просмотре слева направо видим штрихи, которые означают определенную последовательность чисел, начиная от 0 и до бесконечности. Эти штрихи называют точками. Точки, расположенные левее меньше точек, расположенных правее. Отсюда следует, что точка, имеющая меньшую координату на координатном луче, расположена левее точки с большей координатой.
Наименьшее и наибольшее натуральное число
Считается, что 1 – это наименьшее натуральное число из множества всех натуральных чисел. Все числа, расположенные правее него считаются больше предыдущего. Этот ряд бесконечен, поэтому нет наибольшего числа из этого множества чисел.
Двойные, тройные неравенства
Таким же образом выполняются тройные, четверные и так далее неравенства.
Необходимо быть внимательным при составлении двойных неравенств, так как можно произвести его неверно, что повлечет за собой неправильное решение задачи.
Сравнение натуральных чисел
Сравнить два числа — это значит определить, равны они или нет, если нет, то определить, какое из них больше, а какое — меньше.
Равные и неравные натуральные числа
Если записи двух натуральных чисел одинаковы, то говорят, что эти числа равны между собой. Числа, которые равны, называются равными. Если записи двух натуральных чисел отличаются, то говорят, что эти числа не равны. Числа, которые не равны, называются неравными.
Пример. Натуральное число 34 равно числу 34 (их записи одинаковы), а натуральные числа 63 и 67 не равны (их записи различны). Следовательно числа 34 и 34 — равные, а 63 и 67 — неравные.
Равенства и неравенства
Для записи результата сравнения чисел используются следующие знаки:
Запись, которая состоит из математических выражений, между которыми ставится знак = называется равенством.
2 + 3 = 5 — равенство.
2 + 2 = 1 + 1 + 2 — равенство (подобные записи представляют собой равенство двух числовых выражений, и означают равенство значений этих выражений).
Равенства могут быть как верными (например, 5 = 5 — верное равенство), так и неверными (например, 11 = 14 — неверное равенство).
Знаки > и должны быть обращены остриём к меньшему числу.
Запись, которая состоит из математических выражений, между которыми ставится знак > или называется неравенством.
2 8 — неверное неравенство).
Правила чтения равенств и неравенств
Равенства и неравенства читаются слева направо. Левая часть равенства читается в именительном падеже, а правая — в дательном.
Пример. 7 = 7 — семь равно семи.
Левая часть неравенства читается в именительном падеже, а правая — в родительном.
Пример. 11 > 9 — одиннадцать больше девяти, 3 Пример. Сравним числа 1 и 3, 7 и 4. Запишем все однозначные натуральные числа в одной строке в следующем порядке:
Число 1 меньше числа 3 (1 4), так как в натуральном ряду число 7 находится правее числа 4.
Для применения правил сравнения чисел по их десятичной записи необходимо принять одну условность: будем считать, что число 0 меньше любого натурального числа, и что нуль равен нулю.
Правила сравнения натуральных чисел по их десятичной записи:
Если записи сравниваемых чисел состоят из одинакового количества цифр, то числа сравниваются поразрядно слева направо. Большим будет считаться то число, у которого первая (слева направо) из неодинаковых цифр больше.
Когда говорят, что цифры равны (или одна цифра больше другой), то имеют ввиду, что соответствующие им числа равны (или одно число больше другого).
Пример. Сравним натуральные числа 4026 и 4019. Для удобства сравнения можно записать их одно под другим:
Сначала сравниваем значения разряда тысяч. Получаем равенство 4 = 4, поэтому переходим к сравнению значений следующего разряда. Опять получаем равенство 0 = 0, переходим к сравнению значений разряда десятков. Теперь имеем неравенство 2 > 1, из которого делаем вывод, что число 4026 больше числа 4019 (4026 > 4019), потому что у первого числа, цифра разряда десятков (2) больше, чем цифра разряда десятков (1) у второго числа.
Если количество цифр в записи сравниваемых чисел разное, то большим будет считаться то число, у которого количество цифр больше.
Пример. Сравним натуральные числа 347 503 и 34 503. Для удобства сравнения можно записать их одно под другим:
Записав числа одно под другим, можно наглядно заметить, что первое число имеет большее количество цифр, чем второе, следовательно 347 503 > 34 503.
Два натуральных числа равны, если у них одинаковое количество цифр и цифры одинаковых разрядов равны.
Пример. Сравним числа 38 526 734 и 38 526 734. Для удобства сравнения можно записать их одно под другим:
38 526 734
38 526 734
Записи данных чисел одинаковы (количество цифр и цифры одинаковых разрядов равны), следовательно эти числа равны.
Двойные неравенства, тройные неравенства и т. д.
Когда нужно записать, что одно число больше другого, но меньше третьего, часто используют двойные неравенства.
В виде двойного неравенства можно записывать результат сравнения трёх натуральных чисел.
Пример. Допустим, нужно сравнить три натуральных числа 11, 34 и 8. Сравнивая данные числа между собой, получим три неравенства 11 8, которые можно записать как двойное неравенство: