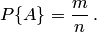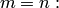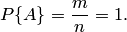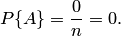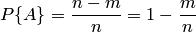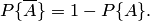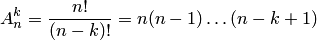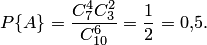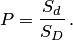Что значит совместные и несовместные события
Теория вероятности. Часть 2
В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.
Совместные и несовместные события
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.
Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.
События называются совместными, если наступление одного из них не исключает наступления другого.
Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.
Сумма событий
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий:
Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:
Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:
Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность совместной реализации первых двух событий по условию равна 0,12.
Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть
Зависимые и независимые события
Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.
Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.
Произведение вероятностей
Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:
Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле:
.
Подборку задач на отработку темы смотрите здесь.
1.2.2. Совместные и несовместные события.
Противоположные события. Полная группа событий
События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий. Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой наверху:
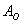
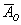
Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.
Противоположные события легко формулируются из соображений элементарной логики:
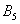
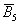
Либо 5, либо не 5, т.е. данные события несовместны и противоположны.
Аналогично:
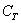
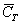
Множество несовместных событий образуют полную группу, если в результате отдельно взятого испытания обязательно появится одно и только одно из этих событий. Очевидно, что любая пара противоположных событий, например, 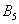
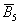
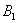
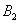
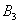
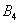
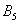
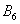
События 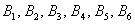
И из этих двух примеров вытекает ещё одно важное понятие, которое нам потребуется в дальнейшем – это элементарность исхода (события). Если совсем просто, то элементарное событие нельзя «разложить на другие события». Например, события 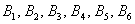
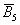
В примере с картами события 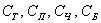
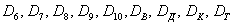
Таким образом, элементарным исходом здесь считается лишь извлечение какой-то конкретной карты, и 36 несовместных элементарных исходов тоже образуют полную группу событий.
И коротко о событиях совместных. События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого. Например:
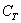
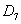
– данные события совместны, т.к. при излечении семёрки треф одновременно имеют место оба события.
Понятие совместности охватывает и бОльшее количество событий:
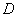
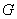
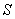
Ситуация, конечно, редкая, но совместное появление всех трёх событий, не исключено. Следует отметить, что перечисленные события совместны и попарно.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Что значит совместные и несовместные события
Раздел 1. Основные понятия теории вероятностей
Классификация событий на возможные, вероятные и случайные. Понятия простого и сложного элементарного события. Операции над событиями. Классическое определение вероятности случайного события и её свойства. Элементы комбинаторики в теории вероятностей. Геометрическая вероятность. Аксиомы теории вероятностей.
Классификация событий
Одним из основных понятий теории вероятностей является понятие события. Под событием понимают любой факт, который может произойти в результате опыта или испытания. Под опытом, или испытанием, понимается осуществление определённого комплекса условий.
– попадание в цель при выстреле из орудия (опыт — произведение выстрела; событие — попадание в цель);
– выпадение двух гербов при трёхкратном бросании монеты (опыт — трёхкратное бросание монеты; событие — выпадение двух гербов);
– появление ошибки измерения в заданных пределах при измерении дальности до цели (опыт — измерение дальности; событие — ошибка измерения).
Можно привести бесчисленное множество подобных примеров. События обозначаются заглавными буквами латинского алфавита 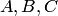
Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Например, подбрасываются две игральные кости. Событие 
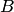

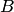

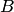

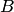
Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.
Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным.
Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия заданному, отказ одного из звеньев автоматизированной системы управления.
События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие. Например, пусть магазину поставляют электролампочки (причем в равных количествах) несколько заводов-изготовителей. События, состоящие в покупке лампочки любого из этих заводов, равновозможны.
Важным понятием является полная группа событий. Несколько событий в данном опыте образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них. Например, в урне находится десять шаров, из них шесть шаров красных, четыре белых, причем пять шаров имеют номера. 
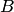
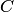
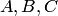
Введем понятие противоположного, или дополнительного, события. Под противоположным событием 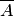


Операции над событиями
При разработке аппарата и методики исследования случайных событий в теории вероятностей очень важным является понятие суммы и произведения событий.
Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
Сумма 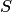
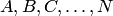
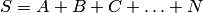
Например, если событие 
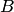
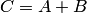
Произведением, или пересечением, нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Произведение 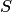
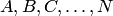
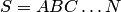
Например, если событие 
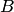
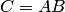
Понятия суммы и произведения событий имеют наглядную геометрическую интерпретацию. Пусть событие 
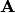
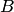
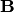
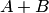
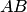
Классическое определение вероятности случайного события
Для количественного сравнения событий по степени возможности их появления вводится числовая мера, которая называется вероятностью события.
Вероятностью события называется число, являющееся выражением меры объективной возможности появления события.
Вероятность события 
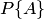
Вероятность события 
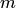
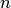
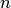
Это есть классическое определение вероятности. Таким образом, для нахождения вероятности события необходимо, рассмотрев различные исходы испытания, найти совокупность единственно возможных, равновозможных и несовместных случаев, подсчитать общее их число 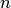
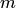
Из формулы (1.1) следует, что вероятность события является неотрицательным числом и может изменяться в пределах от нуля до единицы в зависимости от того, какую долю составляет благоприятствующее число случаев от общего числа случаев:
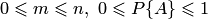
Свойства вероятности
Свойство 1. Если все случаи являются благоприятствующими данному событию 
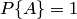
Свойство 2. Если нет ни одного случая, благоприятствующего данному событию 
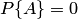
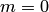
Свойство 3. Вероятность наступления событий, образующих полную группу, равна единице.
Свойство 4. Вероятность наступления противоположного события 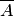

где 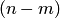

Важное достоинство классического определения вероятности события состоит в том, что с его помощью вероятность события можно определить, не прибегая к опыту, а исходя из логических рассуждений.
Пример 1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.
Решение. Обозначим 

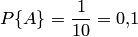
Элементы комбинаторики
В теории вероятностей часто используют размещения, перестановки и сочетания. Если дано множество 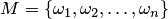
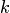
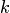
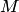
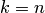
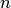
Пусть, например, дано множество 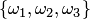
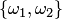
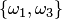
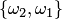
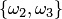
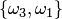
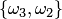
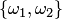
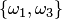
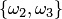
Два сочетания различаются хотя бы одним элементом, а размещения различаются либо самими элементами, либо порядком их следования. Число сочетаний из 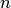
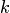
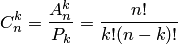
есть число размещений из 
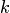
Пример 2. В партии из 10 деталей имеется 7 стандартных. Найти вероятность того, что среди взятых наудачу 6 деталей ровно 4 стандартных.
Решение. Общее число возможных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т. е. равно 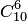

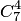
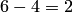
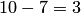
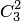
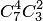
Статистическое определение вероятности
Формулу (1.1) используют для непосредственного вычисления вероятностей событий только тогда, когда опыт сводится к схеме случаев. На практике часто классическое определение вероятности неприменимо по двум причинам: во-первых, классическое определение вероятности предполагает, что общее число случаев 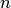
Частота появления событий при многократно повторяющихся Опытах имеет тенденцию стабилизироваться около какой-то постоянной величины. Таким образом, с рассматриваемым событием можно связать некоторую постоянную величину, около которой группируются частоты и которая является характеристикой объективной связи между комплексом условий, при которых проводятся опыты, и событием.
Вероятностью случайного события называется число, около которого группируются частоты этого события по мере увеличения числа испытаний.
Это определение вероятности называется статистическим.
Преимущество статистического способа определения вероятности состоит в том, что он опирается на реальный эксперимент. Однако его существенный недостаток заключается в том, что для определения вероятности необходимо выполнить большое число опытов, которые очень часто связаны с материальными затратами. Статистическое определение вероятности события хотя и достаточно полно раскрывает содержание этого понятия, но не дает возможности фактического вычисления вероятности.
Геометрическая вероятность
В классическом определении вероятности рассматривается полная группа конечного числа равновозможных событий. На практике очень часто число возможных исходов испытаний бесконечно. В таких случаях классическое определение вероятности неприменимо. Однако иногда в подобных случаях можно воспользоваться другим методом вычисления вероятности. Для определенности ограничимся двумерным случаем.
Пусть на плоскости задана некоторая область 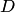
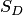
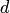
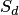
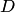
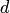
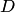
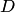
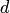
Таким образом, в общем случае, если возможность случайного появления точки внутри некоторой области на прямой, плоскости или в пространстве определяется не положением этой области и ее границами, а только ее размером, т. е. длиной, площадью или объемом, то вероятность попадания случайной точки внутрь некоторой области определяется как отношение размера этой области к размеру всей области, в которой может появляться данная точка. Это есть геометрическое определение вероятности.
Пример 3. Круглая мишень вращается с постоянной угловой скоростью. Пятая часть мишени окрашена в зеленый цвет, а остальная — в белый (рис. 4). По мишени производится выстрел так, что попадание в мишень — событие достоверное. Требуется определить вероятность попадания в сектор мишени, окрашенный в зелёный цвет.
Решение. Обозначим 
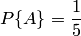
Аксиомы теории вероятностей
Из статистического определения вероятности случайного события следует, что вероятность события есть число, около которого группируются частоты этого события, наблюдаемые на опыте. Поэтому аксиомы теории вероятностей вводятся так, чтобы вероятность события обладала основными свойствами частоты.
Аксиома 1. Каждому событию 
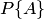
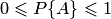
Аксиома 2. Вероятность достоверного события равна единице.
Аксиома 3. Вероятность невозможного события равна нулю.