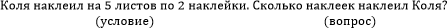Что значит составить математическую модель ситуации в задаче

Что такое математическая модель?

Понятие математической модели.

Например, нам нужно посчитать расходы (Р) на покупки в магазине. Надо купить две булки (Б) и три пачки масла (М). Мы знаем цену булки (ЦБ) и цену масла (ЦМ). Легко можно записать:

Составление (построение) математической модели задачи.

Говоря конкретнее, нужно установить математическую связь между всеми данными задачи.

Но можно выделить три основных момента, на которые нужно обратить внимание.

1. В любой задаче есть текст, как ни странно.) В этом тексте, как правило, имеется явная, открытая информация. Числа, значения и т.п.

3. В любой задаче должно быть дана связь данных между собой. Эта связь может быть дана открытым текстом (что-то равно чему-то), а может быть и скрыта за простыми словами. Но простые и понятные факты частенько упускаются из виду. И модель никак не составляется.

Сразу скажу: чтобы применить эти три момента, задачу приходится читать (и внимательно!) несколько раз. Обычное дело.

Начнём с простой задачки:

Все эти слова нужно превратить в какое-то уравнение. Для этого нужно, повторюсь, установить математическую связь между всеми данными задачи.

С чего начинать? Сначала вытащим из задачи все данные. Начнём по порядочку:

Обращаем внимание на первый момент.

Какая здесь явная математическая информация? 8 рыбин и 20%. Не густо, да нам много и не надо.)

Обращаем внимание на второй момент.

Ищем скрытую информацию. Она здесь есть. Это слова: «20% всех рыбин«. Здесь нужно понимать, что такое проценты и как они считаются. Иначе задача не решается. Это как раз та дополнительная информация, которая должна быть в голове.

Здесь ещё имеется математическая информация, которую совершенно не видно. Это вопрос задачи: «Сколько всего рыбин купил. « Это ведь тоже какое-то число. И без него никакая модель не составится. Поэтому обозначим это число буквой «х». Мы пока не знаем, чему равен икс, но такое обозначение очень нам пригодится. Подробнее, что брать за икс и как с ним обращаться, написано в уроке Как решать задачи по математике? Вот так сразу и запишем:

Возвращаемся к раскрытию информации. Кто не знает, что такое процент, никогда не раскроет, да. А кто знает, тот сразу скажет, что проценты здесь от общего числа рыб даны. А нам это число неизвестно. Ничего не выйдет!

Общее количество рыб (в штуках!) мы не зря буквой «х» обозначили. Посчитать южных рыб в штуках не получится, но записать-то мы сможем? Вот так:

Вот теперь мы скачали всю информацию с задачи. И явную, и скрытую.

Обращаем внимание на третий момент.

Ищем математическую связь между данными задачи. Эта связь настолько проста, что многие её не замечают. Такое часто бывает. Здесь полезно просто записать собранные данные в кучку, да и посмотреть, что к чему.

Вот это уравнение и будет математической моделью нашей задачи.

Прошу заметить, что в этой задаче нас не просят ничего складывать! Это мы сами, из головы, сообразили, что сумма южных и северных рыб даст нам общее количество. Вещь настолько очевидная, что проскакивает мимо внимания. Но без этой очевидности математическую модель не составить. Вот так.

Теперь уже можно применить всю мощь математики для решения этого уравнения). Именно для этого и составлялась математическая модель. Решаем это линейное уравнение и получаем ответ.

Составим математичесскую модель ещё одной задачки:

Спросили Петровича: «А много ли у тебя денег?» Заплакал Петрович и отвечает: «Да всего чуть-чуть. Если я потрачу половину всех денег, да половину остатка, то всего-то один мешок денег у меня и останется. » Сколько денег у Петровича?

Опять работаем по пунктам.

2. Ищем скрытую информацию. Это половинки. Чего? Не очень понятно. Ищем дальше. Есть ещё вопрос задачи: «Сколько денег у Петровича?» Обозначим количество денег буквой «х»:

И вновь читаем задачу. Уже зная, что у Петровича х денег. Вот тут уже и половинки сработают! Записываем:

Остаток будет тоже половина, т.е. 0,5·х. А половину от половины можно записать так:

Теперь вся скрытая информация выявлена и записана.

3. Ищем связь между записанными данными. Здесь можно просто читать страдания Петровича и записывать их математически):

Если я потрачу половину всех денег.

да половину остатка.

Отнимем ещё половину остатка:

то всего-то один мешок денег у меня и останется.

А вот и равенство нашлось! После всех вычитаний один мешок денег остаётся:

Вот она, математическая модель! Это опять линейное уравнение, решаем, получаем:

Задачки, конечно, элементарные. Это специально, чтобы уловить суть составления математической модели. В некоторых задачах может быть гораздо больше данных, в которых легко запутаться. Это часто бывает в т.н. компетентностных задачах. Как вытаскивать математическое содержание из кучи слов и чисел показано на примерах здесь.

В задачах на движение требуется держать в голове формулу-ключ: связь расстояния, скорости и времени. По ссылке можно посмотреть примеры составления модели и решения таких задач.

В задачах на работу надо чётко понимать формулу-ключ: связь времени, производительности труда и объёма работы. Там имеются свои фишки, с которыми можно ознакомиться по ссылке.

Для того, чтобы свободнее ориентироваться в построении математических моделей очень полезно порешать обратные задачи. Т.е. по заданной модели придумать условие задачи. Это, кстати, не так просто.) Тема может быть совершенно любой, фантазия ограничена только математикой. Вот примеры таких заданий:

Составить задачу по математической модели:

х + (х+10) + (х-30) + 20 = 120

Попробуйте придумать задачку, а потом можете найти в уроке Как решать задачи по математике исходную задачу для этой модели. И сравните, для интереса.)

Еще пример, посложнее:

Составить задачу по математической модели:

Исходная задача и её решение приведены в уроке Решение задач на движение. Кстати, по ссылке подробно написано, как эту математическую модель составить.

Составить задачу по математической модели:

1 = 5 · (х + 2х + 2х + 3х + 4х)

Эта задача и её решение расписаны в уроке Задачи на работу.

Ещё одно замечание. В классических школьных задачах (трубы заполняют бассейн, куда-то плывут катера и т.п.) все данные, как правило, подобраны очень тщательно. Там выполняются два правила:
— информации в задаче хватает для её решения,
— лишней информации в задаче не бывает.

В компетентностных и прочих жизненных задачах эти правила строго не соблюдаются. Нету подсказки. Но и такие задачи можно решать. Если, конечно, потренироваться на классических.)

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

А вот здесь можно познакомиться с функциями и производными.

Источник

22. Текстовые задачи Читать 0 мин.

22.112. Математическая модель

Текстовые задачи — это одни из самых нелюбимых заданий, особенно у учеников старших классов, потому что чем дальше, тем запутаннее становится условие, тем сложнее становится составить уравнение и верно решить задачу. Но, как и в любой теме в математике, чтобы уверенно решать сложные задачи, необходимо разобраться с самыми основными приемами.

Разберем эти задачи с самого начала. Текстовая задача состоит из условия, в котором описана некоторая ситуация, и вопроса, на который нужно дать ответ.

Пример:

Решение любой текстовой задачи можно разделить на несколько основных этапов:

Работа с условием

Для облегчения работы с условием полезно использовать иллюстрацию или моделирование. Это может быть краткая запись условия математически или словесно. Также это может быть дополнительный рисунок или таблица.

Пример: Петя выше Коли, Сережа ниже Коли. Кто выше?

Из рисунка сразу понятен ответ: Петя выше всех.

Пример.

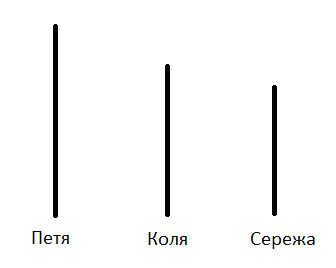
Два поезда идут навстречу друг другу. Скорость одного из них 45 км/ч, скорость другого — 55 км/ч. Сейчас между ними 200 км. Через сколько часов они встретятся?

Пусть х часов — время движения обоих поездов, тогда по рисунку видно, что первый проедет 45х км, а второй — 55х км.

Составим математическую модель:

Для составления уравнения по условию задачи используются различные приемы, в зависимости от данной в условии зависимости величин.

Математическая модель

Математика, в частности, занимается тем, что описывает различные реальные ситуации на математическом языке. В таблице приведены различные ситуации и их математические модели.

y — число мальчиков

Алгебраическая зависимость

Такая зависимость выражается в словах: выше/ниже, больше/меньше, дороже/дешевле, длиннее/короче и т. д.

При составлении уравнения особое значение играют используемые предлоги: «в» и «на».

Пример: Петя выше Коли на 20 см, Сережа ниже Коли на 10 см. На сколько см Петя выше Сережи?

Решение: Пусть П — рост Пети, К — рост Коли, С — рост Сережи.

Кстати, обратите внимание на этот приём — выбирать «говорящие» переменные, а не безликие иксы и игреки, чтобы не запутаться при работе с уравнением.

Выразим рост мальчиков.

Петя выше Коли на 20 см: П – 20 = К

Сережа ниже Коли на 10 см: К = С + 10

Подставим в первое уравнение рост Коли: П – 20 = С + 10

Нам нужно найти, на сколько см Петя выше Сережи: П – С

Получаем, что Петя выше Сережи на 30 см.

Пример: На уроке труда ученики делали снежинки. Всего было сделано 12 снежинок. Маша сделала в два раза больше снежинок, чем Коля. Коля сделал на 4 снежинки меньше, чем Рома. Сколько снежинок сделала Маша?

Пусть М — количество снежинок, которое сделала Маша, К — снежинки Коли, Р — снежинки Ромы.

Маша сделала в два раза больше снежинок, чем Коля: К = М/2

Коля сделал на 4 снежинки меньше, чем Рома: Р = К + 4 = М/2 + 4

Вместе ребята сделали 12 снежинок: М + К + Р = 12

Подставим все выраженные через М значения: М + М/2 + М/2 + 4 = 12

Маша сделала 4 снежинки.

Процентная зависимость

С процентами нам постоянно приходиться сталкиваться в повседневной жизни. “Скидка 30%”, “Кредит без процентов за 5 минут”, “Арендная плата выросла на 12%” — со всех сторон на нас сыпятся рекламные слоганы и призывы. Но что же значит это таинственное слово “проценты”? И как ими оперировать?

Сегодня мы с вами дадим определение процентов, поймём, как находится процент от некоторого числа, как можно найти одно количество процентов, уже зная другое. И, конечно, рассмотрим каждый из этих случаев на конкретном примере.

Как кирка у каменщика, камертон у настройщика или световой меч у Джедая, в математике тоже существуют свои инструменты, нужные для выполнения тех или иных операций. И проценты как раз и являются таким удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби. И действительно, проценты очень тесно связаны с дробями, по сути, основываясь на них.

Так что же такое один процент?

Процент — это всегда доля какого-то числа.

Чтобы найти 1%, необходимо поделить всё число на 100.

Пример:

Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом — соответствующие проценты.

Пример:

Пропорция отражает зависимость величин. По-другому это можно записать в виде двух дробей.

Исходя из правил работы с дробями, получаем правила работы с пропорцией.

1. Внутри одной дроби можно сокращать значения.

2. Произведение накрест лежащих значений равно: 200 · 1 = 2 · 100

Эту тему мы еще подробно пройдем на курсе.

Рассмотрим несколько примеров работы с процентами в текстовых задачах.

Ситуация при работе с процентами усложняется, когда изначально нам известен не 1%, а несколько — например, 20. А требуют найти какое-нибудь неудобное число процентов

Пример: 38% населения деревни — это 76 человек. Сколько человек составляет 15% от общего населения?

Так как мы не можем сразу найти 15%, то нам вначале понадобится сделать промежуточный шаг — найти 1%. Если 38% — это 76 человек, то, разделив на 38, мы получим так нужный нам 1%. 38% = 76 человек ⇒1% = 2 человека. Тогда 15% = 30 человек

Но неугомонные математики не остановились и на этом. Что будет, если мы возьмём процент от какого-то числа, вычтем или прибавим к начальному числу, а затем снова возьмём то же количество процентов?

Пример: В 2010 дом стоял 2 тысячи рублей. В 2011 его цена увеличилась на 20%, а в 2012 — ещё на 20%. Сколько дом стоил к концу 2012 года?

На примере этой задаче мы посмотрим не только на то, как нужно брать проценты от разных величин, но и как переводить проценты в дроби. Решим её двумя способами:

Способ 1 Для начала давайте выясним, сколько стоил дом в 2011. Его стоимость увеличилась на 20%, т.е. на 400 рублей (1% = 2000:100 = 20, 20% = 400) и стала, соответственно, равна 2400. Теперь нам нужно узнать, сколько он стал стоить в 2012. Важно! Сейчас мы будем брать 20% от новой цены, т.е. той, которая была на дом в 2011 году. Если 1% = 2400:100 = 24, то 20% = 480, то есть новая цена в 2012 году — 2400 + 480 = 2880

Способ 2 Если 1% — это 0,01 от чего-то, то 20% — это 0,2. Тогда 20% от первоначальной цены это 2000⋅0,2 = 400, и цена на дом в 2011 году стала 2400. Теперь находим 20% от новой стоимости 2400⋅0,2 = 480 и итоговую стоимость в 2012 году: 2400 + 480 = 2880

Отлично! Итак, мы не только узнали, что такое проценты, как можно с ними обращаться, но и выяснили, как можно брать проценты от разных величин и как сопоставлять проценты с дробями. Больше интересных фактов и приёмов работы с процентами вы узнаете в процессе курса.

Также текстовые задачи могут быть посвящены прогрессиям, производительности, темпу — обо всем этом мы поговорим на нашем курсе. А сейчас приступайте к задачам для тренировки.

Источник

Конспект на тему «Математические модели реальной ситуации»

На этом уроке мы разберем, как решать задачи с помощью систем линейных уравнений, научимся переводить условия задач на математический язык и строить математические модели.

Решим такую задачу. (См. Рис. 1.)

Рис. 1. Условие задачи

В задаче речь идет о трех объектах: о кролике, птице и кабане, и неизвестными величинами являются массы этих зверей.

Сумма трех кроликов – это три кролика. Можно продолжать с картинками, но это неудобно.

Заменим массу животных на переменные (см. Рис. 2):

Рис. 2. Условные обозначения

Перепишем все, что показано на картинке, с помощью переменных:

Решим полученную систему:

Тогда получаем, что масса трех животных:

Нам нигде не пришлось думать, решать задачу. Главное, что нужно было сделать – аккуратно переписать условие задачи с помощью введенных обозначений. Таким образом, мы построили математическую модель – записали условие задачи на математическом языке и решили ее абсолютно автоматически.

Все задачи, которые будут встречаться в дальнейшем, решаются по одному алгоритму. Итак, рассмотрим этот алгоритм. В нем выделим 4 пункта.

Читаем внимательно задачу и представляем, что происходит. Перечисляем всех участников и их характеристики (величины), которые можно измерить.

Вводим обозначения для всех этих величин. Переписываем все, что сказано в условии задачи, с помощью этих обозначений. Получаем набор алгебраических условий, уравнений, который мы называем моделью.

Решаем полученные уравнения. Получаем ответ в рамках модели.

Возвращаемся от модели к задаче. Даем ответ на вопрос задачи.

Два туриста вышли одновременно из двух городов, расстояние между которыми – км, и встретились через ч. С какой скоростью шел каждый турист, если первый прошел на км больше, чем второй?

1 этап. Что происходит?

Два туриста идут навстречу друг другу и встречаются. Каждый прошел какое-то расстояние, у каждого есть скорость движения, каждый потратил какое-то время. Еще есть общее расстояние между городами. (См. Рис. 3.)

Рис. 3. Иллюстрация к задаче

Итак, для каждого участника есть три величины и еще общее расстояние:

Итак, 7 величин, 7 обозначений. (См. Рис. 4.) Пока нас не интересовало, какие из них уже известны, а какие нет.

Рис. 4. Условные обозначения

А как же быть с и ? Будем ли мы вводить эти обозначения? Для задач на движение есть уже свои всем понятные обозначения: – расстояние, – скорость, – время. И заменять их на и нет никакого смысла. А вообще это совершенно неважно. Делайте такие обозначения, чтобы вам было удобно и понятно.

Теперь нам нужно переписать условие задачи, используя введенные обозначения.

– вышли одновременно и встретились через ч.

– расстояние между городами км.

– вышли из двух городов и встретились.

– первый прошел на км больше, чем второй.

Найти нужно скорости каждого туриста.

Кроме того, что сказано в задаче, мы владеем еще кое-какой важной информацией. А именно, как связаны все эти величины друг с другом. Запишем эти соотношения для каждого туриста:

Итак, мы получили математическую модель – ввели обозначения и с помощью них переписали условие задачи. То есть мы уже выполнили всей работы.

Наша модель содержит уже всю информацию. Никакой новой информации не будет, и никакая не пропадет. Мы просто займемся переписыванием ее в эквивалентном, но более удобном виде.

Итак, надо найти , .

Для начала уменьшим количество записей в модели. Для этого подставим все известные величины.

Нам известны , и . Получаем:

Нижние два уравнения содержат величины, которые мы ищем. Но здесь неизвестных, и если эти два уравнения взять в качестве системы, то у неё будет бесконечно много решений.

Верхние два уравнения содержат только две неизвестные. Правда, там нет нам нужных, но если решить систему этих двух уравнений, мы найдем , , а затем уже и , из нижних двух.

То есть в качестве системы берем два верхних уравнения.

Решим систему методом сложения. Сложим почленно оба уравнения – получим первое уравнение новой системы, вычтем из первого второе – получим второе уравнение новой системы:

Нашли . Теперь подставим их в два оставшихся уравнения.

Итак, смоделированную задачу мы решили, остался последний этап.

Возвращаемся к исходной задаче. Заменяем наши обозначения на названия величин.

Ответ: скорость первого пешехода – , скорость второго пешехода – .

На двух полках книг. Если переставить со второй полки половину книг на первую, то на первой станет в раза больше, чем останется на второй. Сколько книг на каждой полке?

1 этап. Что происходит?

На двух полках стоят книги. (См. Рис. 5.)

Рис. 5. Размещение книг до перестановки

С одной полки переносят часть книг на другую. (См. Рис. 6.)

Рис. 6. Размещение книг после перестановки

Рис. 7. Количества книг на полках до перестановки

Рис. 8. Количества книг на полках после перестановки

Запишем все условия в этих обозначениях.

– на двух полках книг.

– со второй полки переставили половину книг на первую.

– со второй полки переставили половину книг на первую.

– на первой полке в раза больше книг, чем на второй.

Можно еще написать, что после перестановки общее количество книг не изменилось:

Мы построили модель. Пока мы будем решать эту уже математическую задачу, не станем вспоминать про книги и полки.

Итак, мы хотим получить систему из двух уравнений с двумя неизвестными. Лучше, чтобы это были и , так как именно их нам нужно найти.

Первое уравнение нам для этого подходит. А все остальные содержат еще или или . Но можно заметить, что если в уравнение подставить выражения для и , то мы получим второе уравнение для и .

Составим и решим систему:

Из верхнего уравнения вычтем нижнее:

Мы получили ответ для модели, теперь возвращаемся к задаче.

На первой полке было книги, на второй – .
В самом деле, если половину книг со второй полки переставить на первую, то на второй останется , а на первой станет , то есть в раза больше.

На самом деле, совершенно не обязательно при составлении модели должно получаться два уравнения с двумя неизвестными. Их может быть и , и .

Системы уравнений с большим количеством переменных.

На самом деле, переменных столько, сколько мы ввели обозначений. Если обозначений , то и уравнений должно быть . Такой подход отличается от предыдущих только своей большей формальностью.

Посмотрим на первую задачу с этой точки зрения.

Два туриста вышли одновременно из двух городов, расстояние между которыми – км, и встретились через ч. С какой скоростью шел каждый турист, если первый прошел на км больше, чем второй?

1 этап. Что происходит?

Мы это уже все обсудили. Ничего нового.

Два туриста идут навстречу друг другу и встречаются. Каждый прошел какое-то расстояние, у каждого есть скорость движения, каждый потратил какое-то время. Еще есть общее расстояние между городами. (См. Рис. 9.)

Рис. 9. О чем задача

Мы ввели обозначений: , , , , , , . Можно сказать, что это переменных. Нам необходимо для решения уравнений.

Вспомним, какие у нас были выписаны условия.

Посчитаем, сколько у нас уравнений. Вроде бы , последняя запись – вообще не уравнение.

На самом деле, верхняя строчка – это два уравнения, их можно расписать по отдельности, и получим систему из линейных уравнений с неизвестными.

Решается она точно такими же методами, как система с двумя уравнениями, – подстановка и сложение.

Верхние три уравнения уже имеют очень хороший вид, их трогать не будем, но подставим их в остальные.

Внутри большой системы можно увидеть систему поменьше.

Если сложить и строки, то пропадет . Тогда легко увидеть, что . Это условие можно записать вместо любого из двух, откуда мы это и получили.

Нужно следить, чтобы уравнений оставалось .

Теперь легко найти .

Остались два нижних уравнения. Подставим туда значения и .

Находим оставшиеся неизвестные.

Конечно, ответ не зависит от выбранного способа решения: скорость первого пешехода – , скорость второго пешехода – .

Какие преимущества и недостатки у этого подхода по сравнению с первым?

Преимущества: этот метод более автоматизирован, он ближе к идеальному алгоритму. Нужно только ввести обозначения и написать соответствующее количество уравнений.

Недостатки: может оказаться, что проделано много лишней работы. Ведь обычно нам нужны не все переменные, а этот метод предлагает найти все.

За часа по течению и часа против течения теплоход проходит км. За ч по течению и мин против течения теплоход проходит км. Найдите собственную скорость теплохода и скорость течения.

1 этап. Что происходит?

Итак, у нас два независимых события: теплоход первый раз плывет по течению и против него одно и то же расстояние, и второй раз, тоже по течению и против него, но уже другое расстояние.

У нас 4 промежутка времени , , ,

Два расстояния, две скорости – реки и теплохода , , ,

Перепишем все условия в наших обозначениях. Нам известны все 4 промежутка времени. Запишем их.

Теперь первый заплыв:

Он проплыл 380 км, причем эти 380 км состоят из двух частей. Первая часть та, что он проплыл по течению, очевидно, со скоростью . Мы можем записывать время, которое он плыл по течению, как , но так как мы знаем его, то можно писать уже само значение, часа. И второе слагаемое – расстояние, пройденное против течения.

Теперь то же самое мы можем записать для второго заплыва.

Итак, два длинных уравнения в нашей модели дают нам систему двух уравнений с двумя неизвестными:

Решим ее. Раскроем скобки:

Умножим обе части нижнего уравнения на 2, чтобы избавиться от дробных коэффициентов:

Сложим почленно уравнения, пропадет переменная :

Найдем :

Подставим во второе уравнение.

Мы получили ответ для модели, возвращаемся к задаче.

Скорость теплохода – .

Скорость течения реки – .

Итак, как устроен наш единый алгоритм для решения задач.

1. Что происходит?
Внимательно читаем задачу и представляем, что происходит. Обязательно нужно представить все до конца и всех участников событий.

2. Моделирование
Вводим обозначения для всех величин, которые есть в задаче. Аккуратно переписываем условия задачи с введенными обозначениями. Это главный навык, который мы должны натренировать.

3. Решение
Решаем уравнения в нашей модели.

4. Ответ
Возвращаемся к задаче, формулируем ответ.

Еще одна рекомендация. Она относится не только к решению такого рода задач, а вообще к занятию математикой.

Даже если вы не пишете контрольную работу, а просто решаете задачу для себя, обязательно оформляйте все аккуратно, пишите разборчиво. Очень часто не удается решить задачу из-за того, что оформление было сделано небрежно и вам самим не понятно, что у вас написано. Аккуратность в оформлении математической записи нужна не вашему учителю, а вам самим.

Источник