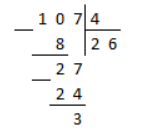Что значит смешанное число в дробях
Смешанные дроби
Что такое смешанная дробь
Число, содержащее в себе целую и дробную части, называется смешанной дробью.
По сути, данное понятие представляет собой сумму целого числа и правильной дроби:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Превращение смешанной дроби в неправильную
Любое смешанное число можно преобразовать в неправильную дробь. Для этого необходимо к произведению целой части и знаменателя дробной части прибавить числитель. Полученная сумма будет числителем неправильной дроби, а знаменатель останется прежним.
Преобразование смешанной дроби в неправильную можно записать в виде формулы:
Выполнение действий со смешанными дробями, формулы и примеры
Сложение
Чтобы посчитать сумму смешанных дробей необходимо отдельно сложить их целые компоненты и дробные составляющие. Правильные дроби в составе смешанных чисел суммируются при помощи приведения к наименьшему общему знаменателю.
Формульное выражение сложения смешанных чисел:
\(a\frac bc+d\frac ef=\left(a+d\right)+\left(\frac bc+\frac ef\right)\)
Вычисляем наименьший общий знаменатель дробных слагаемых:
Вычитание
Чтобы из одной смешанной дроби вычесть другую, нужно дробные компоненты уменьшаемого и вычитаемого привести к минимальному общему знаменателю, затем выполнить вычитание отдельно целых и дробных частей.
Формула для ситуации, когда дробь в составе уменьшаемого больше, чем дробная часть вычитаемого:
\(a\frac bc-d\frac ef=\left(a+\frac bc\right)-\left(d+\frac ef\right)\;=\left(a-d\right)+\left(\frac bc-\frac ef\right)\)
В случае, когда дробь в составе уменьшаемого меньше дроби в составе вычитаемого, необходимо меньшую дробь превратить в неправильную, отняв единицу от целой части уменьшаемого, то есть:
\(a\frac bc-d\frac ef=\left(\left(a-d\right)-\frac ef\right)+\frac bc\)
Для решения этого выражения найдем наименьший общий знаменатель:
8=2×2×2, следовательно, 8 — это наименьший общий знаменатель.
Умножение и деление
Перед тем, как умножать или делить смешанные числа, необходимо преобразовать их в неправильные дроби. После этого можно производить нужное действие по правилам умножения и деления обыкновенных дробей.
Формула умножения смешанных чисел выглядит так:
Формула деления смешанных дробей:
При умножении смешанной дроби на натуральное число преобразование в неправильную дробь делать не нужно. Такого рода вычисления производятся с помощью распределительного закона умножения.
Если требуется разделить смешанную дробь на натуральное число или натуральное число на смешанную дробь, нужно представить делимое и делитель в виде неправильной дроби, затем выполнить необходимое действие, как с обыкновенными дробями.
Если нужно выполнить умножение или деление смешанной дроби на обыкновенную дробь, смешанное число необходимо преобразовать в неправильную дробь. После преобразований нужное действие производится по такому же алгоритму, как с обыкновенными дробями.
Смешанные числа — сложение, вычитание и умножение дробей с разными знаменателям
Что такое смешанное число
Под смешанным числом понимают сумму натурального числа и обычной дроби, записанную без знака «+».



Где 4 ― это целая, а 5/7 ― дробная часть.
Как представить смешанное число в виде неправильной дроби
Если мы, имея на руках один пирог и ещё половину (то есть 1½), возьмём и дополнительно поделим целый пирог на два равных куска, то у нас в итоге окажется три половинки (или 3/2). Но суть от этого всё равно не изменится: «количество» пирога останется прежним.

Этот пример наглядно показывает, что смешанное число можно превратить в неправильную дробь. Это преобразование можно выполнить за несколько шагов:
Например, 5¾ преобразуется следующим образом:

Данные вычисления можно выразить и в более короткой формуле:


Как выделить целую часть неправильной дроби
Чтобы совершить обратную операцию и превратить неправильную дробь в смешанное число, нужно сначала выделить её целую часть. Она будет равна результату деления числителя на знаменатель.

Если поделилось без остатка, значит больше никаких действий выполнять не нужно.
Если поделить без остатка не получается, то для завершения преобразования в смешанное число, остаток следует вынести в числитель. Знаменатель остаётся тем же.

Как перевести смешанную дробь в десятичную
Так как подобную процедуру часто приходится проделывать не только в школе, выполняя математические задания и решая различные уравнения, но и в повседневности, ― умение проделывать это легко и быстро может оказаться очень полезным.

Для перевода необходимо:
Таким образом, чтобы преобразовать 53/5, нужно:

Как сократить смешанную дробь

При сокращении целая часть не трогается, изменениям подвергается только дробная. Чтобы сократить её, нужно:
Например, чтобы сократить 76/9, необходимо:

Сложение смешанных чисел
Чтобы осуществить сложение, нужно необходимую операцию проделать отдельно для целых и отдельно для дробных частей. А получившиеся результаты сложить.
Например, чтобы решить следующий пример



Вычитание смешанных чисел
Для вычитания вычисления аналогичны. Следующую задачу

следует решить так:
Как умножать смешанные числа
Чтобы перемножить смешанные числа, необходимо:
Для примера решим следующее задание:


Заключение
Происхождение чисел сложно точно проследить. Известно только, что человек стал пользоваться ими с самых седых времён. История дробей также берёт своё начало в глубокой древности: подобными понятиями оперировали уже в древнем Египте.
Сегодня просто невозможно представить нашу жизнь без них. Все современные научные достижения, на которых основано наше общество, были бы попросту неосуществимы, не говоря уже о том, что значительно усложнилась бы наша повседневная жизнь. Вот почему так важно знать, что они собой представляют.
Смешанные дроби или смешанные числа.
Смешанные дроби в математике можно получить одним из способов, например, из неправильной дроби или путем сложения дробей и еще много вариантов, когда вы сможете столкнуться со смешанной дробью.
Как сделать из неправильной дроби правильную дробь?
Рассмотрим неправильную дробь \(\frac<21><9>\)
Дробная черта — это деление, поэтому число 21 поделим на 9 столбиком.

Получаем дробь \(2\frac<3><9>\), такие дроби называются смешанными. В этой смешанной дроби число 2 – целая часть, а \(\frac<3><9>\) – правильная дробь.
Смешанные дроби состоят из целой и дробной части.
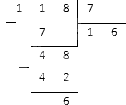
Рассмотрим еще одну неправильную дробь \(\frac<76><5>\)
Разделим ее столбиком:

Как смешанную дробь перевести в неправильную дробь?
Чтобы из смешанной дроби сделать неправильную дробь нужно знаменатель умножить на целую часть и сложить с числителем, получим числитель неправильной дроби. А знаменатель остается без изменения. Рассмотрим пример:
Вопросы по теме:
Смешанная дробь может быть меньше единицы?
Ответ: нет, потому что смешанную дробь можно представить в виде неправильной дроби, а неправильная дробь всегда больше или равна единицы.
Что показывает целая часть у смешанной дроби?
Ответ: целая часть показывает сколько полных знаменателей содержит дробь.
Как представить смешанное число в виде неправильной дроби?
Ответ: к произведению знаменатели и целой части прибавить числитель получим числитель искомой неправильной дроби, а знаменатель не меняется.
Как перевести неправильную дробь в смешанное число? И как выделить целую часть?
Ответ: делим в столбик числитель на знаменатель, неполное частное – это целое, делитель – это знаменатель, а остаток – это числитель. Смотрите пример выше.
Что такое смешанные дроби или смешанные числа?
Ответ: Смешанные дроби – это числа, которые состоят из целой и дробной части.
Пример №1:
Представьте дробь в виде смешанного числа: \(\frac<508><17>\)
Решение:
Разделим дробь столбиком:
Ответ: Получили смешанную дробь \(29\frac<15><17>\)
Пример №2:
Представьте число в виде неправильной дроби: а) \(9\frac<2><3>\), б) \(1\frac<3><7>\)
Решение:
а) \(9\frac<2> <3>= \frac<9 \times 3 +2> <3>= \frac<29><3>\\\\\)
б) \(1\frac<3> <7>= \frac<1 \times 7 +3> <7>= \frac<10><7>\\\\\)
Задача №1:
Миша готовился к экзамену. За месяц он решил 120 задач. За первую неделю Миша решил \(\frac<2><5>\) от этого числа. Сколько задач решил Миша за первую неделю?
Решение:
У нас есть дробь \(\frac<2><5>\), знаменатель равен 5 это значит, что общее число 120 надо разделить на 5 и получим сколько составляет одна часть.
\(120 \div 5 = 24\) задачи это одна часть или \(\frac<1><5>\)
В числителе стоит 2, значит нам надо взять две части, поэтому 24 умножаем на 2.
\(24 \times 2 = 48\) задач
Ответ: за неделю Миша решил 48 задач.
Смешанные дроби
Вы будете перенаправлены на Автор24
Определение смешанной дроби
Перевод смешанного числа в неправильную дробь
Алгоритм перевода смешанного числа в неправильную дробь:
Готовые работы на аналогичную тему
Решение.
Воспользуемся алгоритмом перевода смешанного числа в неправильную дробь.
Запишем краткую запись данного решения:
Решение.
Выделение целой части из неправильной дроби
При получении числового решения не принято оставлять ответ в виде неправильной дроби. Неправильная дробь преобразуется в равное ей натуральное число (если числитель делится нацело на знаменатель), или выделяют целую часть из неправильной дроби (если числитель не делится нацело на знаменатель).
Выделением целой части из неправильной дроби называется замена дроби равным ей смешанным числом.
Решение.
Выполним деление в столбик:
Сложение смешанного числа и натурального числа
Правило сложения смешанного и натурального числа:
Для сложения смешанного и натурального числа нужно к целой части смешанного числа прибавить данное натуральное число, дробная часть остается без изменения:
Решение.
Сложение двух смешанных чисел
При сложении двух смешанных чисел складываются их целые части и дробные части.
Решение.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 21 06 2021
Смешанные числа, перевод смешанного числа в неправильную дробь и обратно
В этом материале мы разберем такое понятие, как смешанные числа. Начнем, как всегда, с определения и небольших примеров, потом поясним связь смешанных чисел и неправильных дробей. После этого мы изучим, как правильно выделять целую часть из дроби и получать в результате целое число.
Понятие смешанного числа
Числа вида 0 3 14 также не относятся к смешанным. Здесь не выполняется первая часть условия: целая часть должна быть представлена только натуральным числом, а нуль им не является.
Как соотносятся между собой неправильные дроби и смешанные числа
Эту связь проще всего проследить на конкретном примере.
Наш пример доказывает, что в виде смешанного числа можно представить любую неправильную дробь.
Мы поняли, как приводить неправильную дробь к виду смешанного числа. Если в числителе неправильной дроби стоит такое число, которое можно разделить на знаменатель без остатка, то можно сделать это, и тогда наша неправильная дробь станет натуральным числом.
Как перевести смешанное число в неправильную дробь
Чтобы успешно решать задачи, полезно уметь производить и обратное действие, то есть делать из смешанных чисел неправильные дроби. В этом пункте мы разберем, как правильно это сделать.
Для этого нужно воспроизвести следующую последовательность действий:
1. Для начала представляем имеющееся смешанное число n a b как сумму целой и дробной части. Получается n + a b
2. Далее заменяем целую часть на дробь со знаменателем, равным единице (то есть записываем n как n 1 ).
Разберем это действие на конкретном примере.
Представьте 5 3 7 в виде неправильной дроби.
Решение
Последний шаг – сложение дробей, имеющих разные знаменатели:
5 1 + 3 7 = 35 7 + 3 7 = 38 7
Представьте 15 2 5 в виде неправильной дроби.
Решение
Как выделить из неправильной дроби целую часть
Обычно мы не указываем неправильную дробь в качестве итогового ответа. Принято доводить вычисления до конца и заменять ее либо натуральным числом (разделив числитель на знаменатель), либо смешанным числом. Как правило, первый способ используется, когда разделить числитель на знаменатель можно без остатка, а второй – если такое действие невозможно.
Когда мы выделяем из неправильной дроби целую часть, мы просто заменяем ее равным смешанным числом.
Разберем, как именно это делается.
Приведем доказательство этого утверждения.
Выделение целой части из неправильной дроби a b осуществляется таким образом:
1) производим деление a на b с остатком и записываем неполное частное q и остаток r отдельно.
Представьте 107 4 в виде смешанного числа.
Решение
Делим 104 на 7 столбиком:
Нам осталось посмотреть, как заменить неправильную дробь натуральным числом (при условии, что ее числитель делится на знаменатель без остатка).