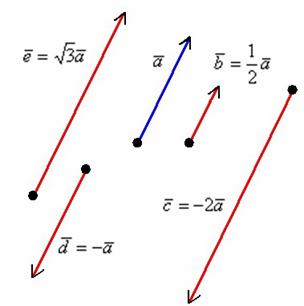
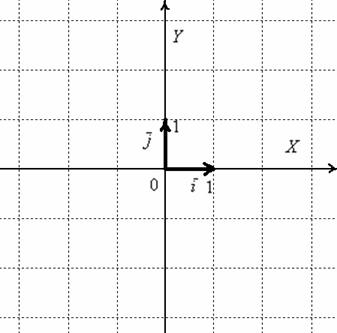
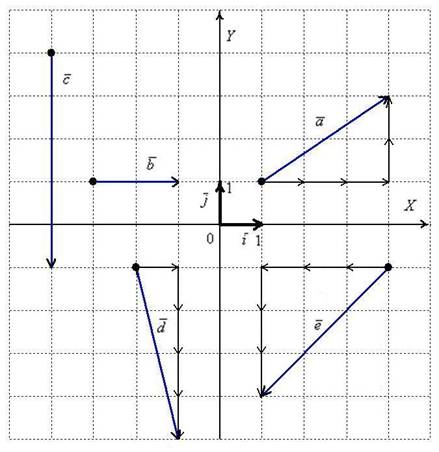
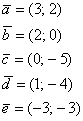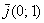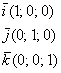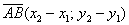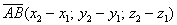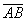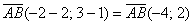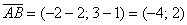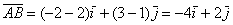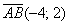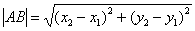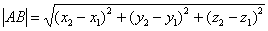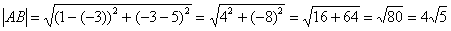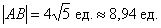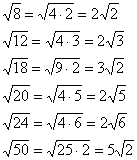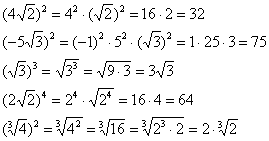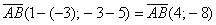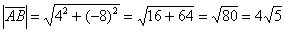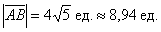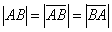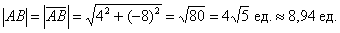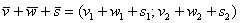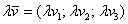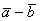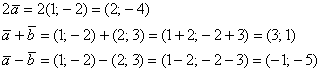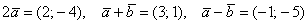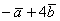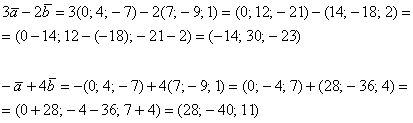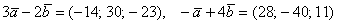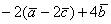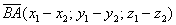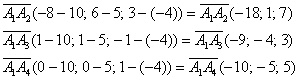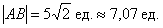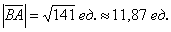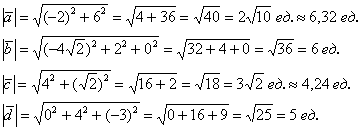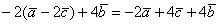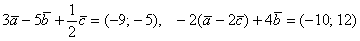Что значит сложение векторов в модуле
5.6.3 Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число
Видеоурок 1: Понятие вектора
Видеоурок 2: Равенство векторов
Видеоурок 3: Сложение и вычитание векторов
Видеоурок 4: Умножение вектора на число
Лекция: Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число

Вектор – это тело, которое изучается в математике, но используется в большом количестве наук. Например, в физике существуют скалярные величины (те, что характеризуются значением – масса, температура и т.д.), а также векторные величины (сила, работа и другие).
Вектор – это величина, которая характеризуется не только значением, но и направлением. Иными словами, это направленный отрезок.
Но кроме его длины, нам также важно, где находится его начало, а где конец.
Если вектор имеет свое начало в некоторой точке А, а заканчивается в точке В, то его обозначают следующим образом:
Кроме двух букв, вектор можно обозначить одной буквой со значком вектора сверху.
Длиной вектора (его модулем) называют расстояние между концом вектора и его началом.
Для определения модуля вектора следует воспользоваться следующей формулой:
Кроме этого, модуль вектора может обозначаться следующим образом:
Если некоторый вектор имеет начало и конец в одной и той же точке, то такой вектор называют нулевым. Нулевой вектор обозначают, как
Если длина некоторого вектора равна единичному отрезку, то его называют единичным.
Если некоторые векторы расположены на одной прямой или же параллельны друг другу, то такие векторы называются коллинеарными.
Если некоторые векторы можно назвать коллинеарными, но кроме этого они направлены в одну сторону, то их можно назвать сонаправленными.
Если же наоборот два коллинеарных вектора смотрят в разные стороны, то их называют противоположно направленными.
Если же некоторые векторы являются коллинеарными, сонаправленными, а также имеют одинаковую длину (модуль), то их можно назвать равными.

Для нахождения координаты вектора следует вычесть соответствующие координаты его конца и начала.
Например, если начало вектора А (3; 6), а конец В (5;9), то этот вектор будет иметь следующие координаты: <2;3>.

Чтобы сложить два вектора для получения нового, необходимо сложить соответствующие координаты.
Например, сложим вектор <2;3>с вектором <5;7>. В результате получим новый вектор с координатами <7;10>. С вычитанием все аналогично.

Чтобы умножить вектор на некоторое число, следует умножить каждую его координату на данное число.
Операции с векторами
Как сложить и перемножить векторы (и зачем).
Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.
Напомним основные мысли:
С векторами можно совершать некоторые математические операции. Вот о них и поговорим.
Правильно — векторы
Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».
Сложение
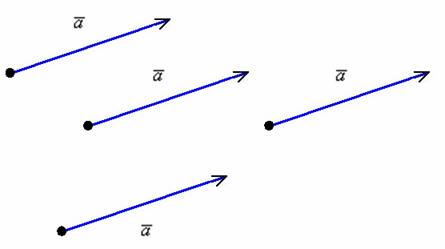
Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.
Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).
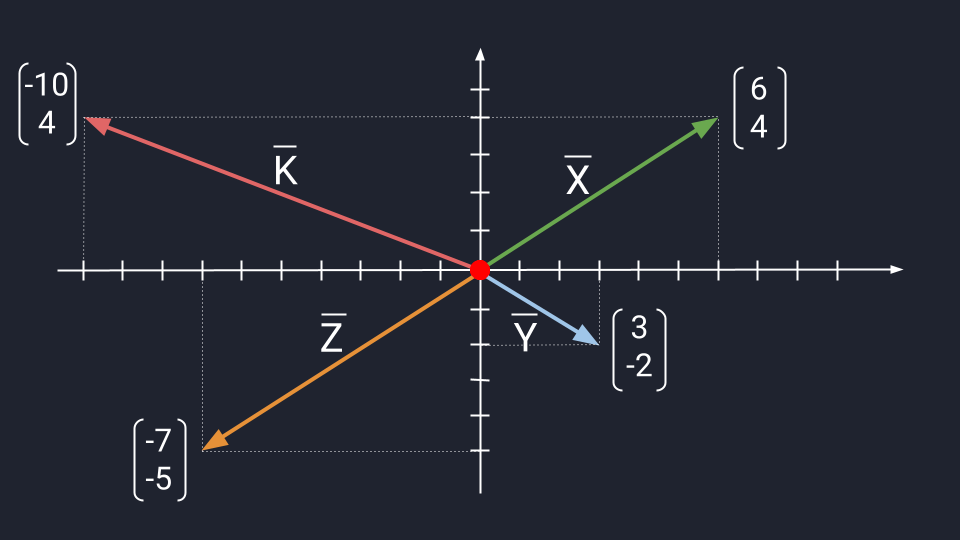
Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.
Предположим, нам нужно сложить векторы X и Y.
X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)
Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.
Например, вот сложение векторов с пятью координатами:
Интуитивное изображение сложения
Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.
Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.
Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.
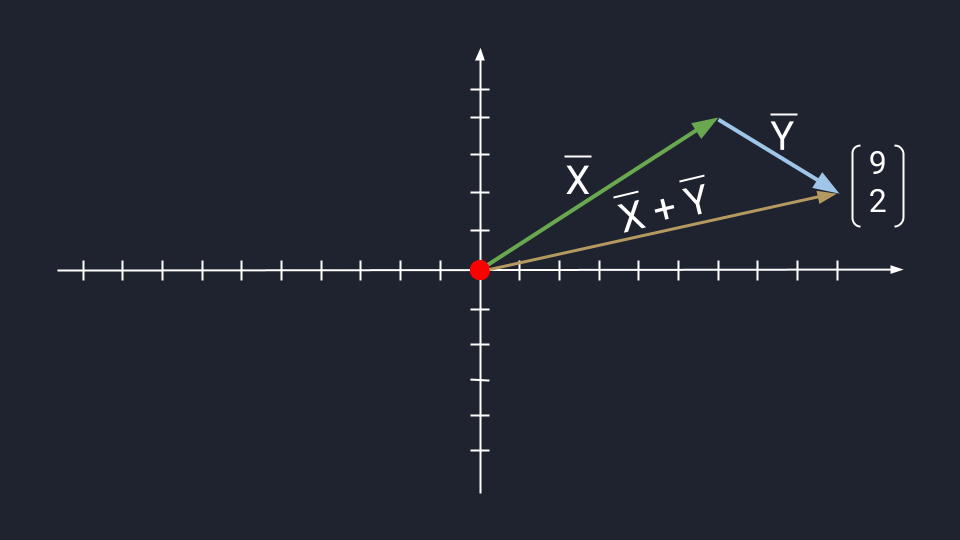
Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.
Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.
Вычитание
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)
Дальше используются правила сложения. Пошагово это выглядит так:
Теперь посмотрим, как выглядит вычитание векторов на графике:
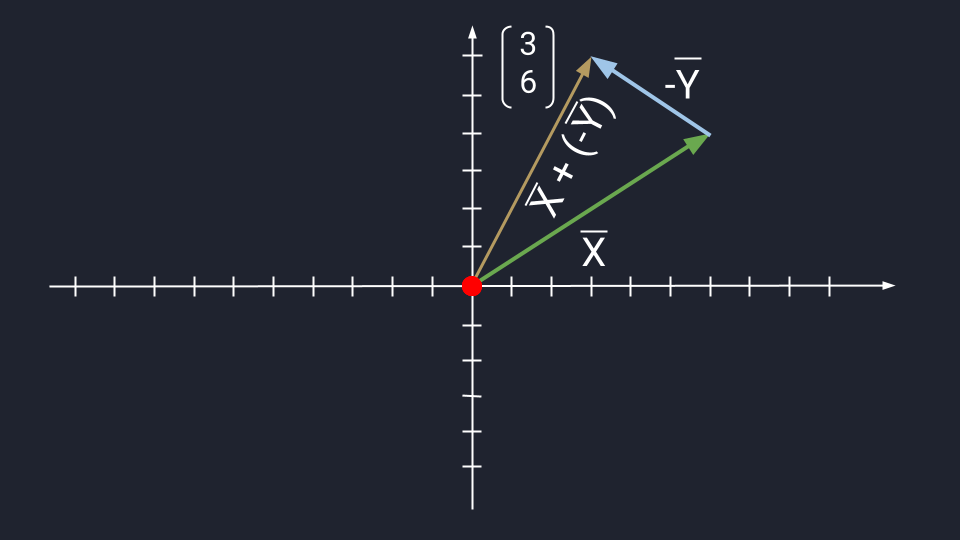
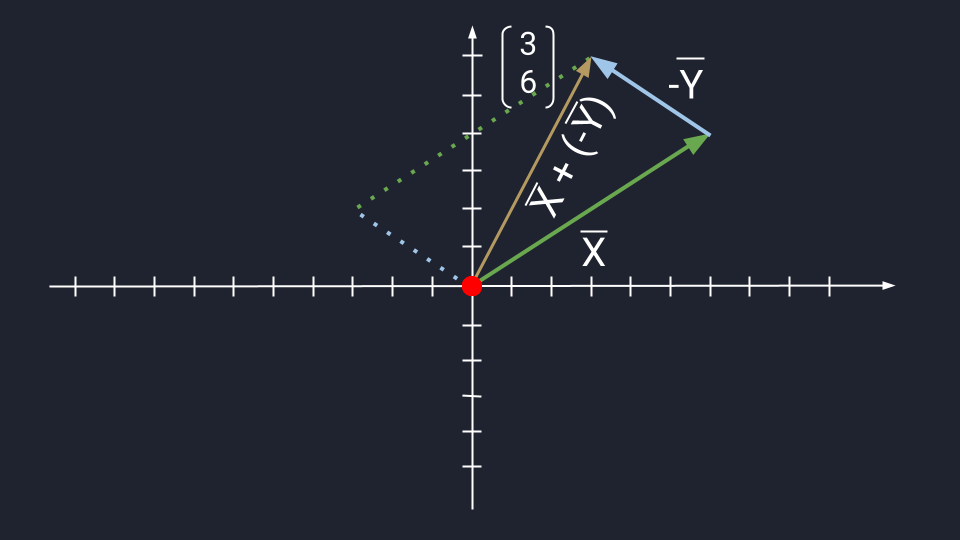
Длина вектора
Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.
Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:
X = 6 − 2 = 4
Y = 5 − 2 = 3
Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:
|C|2 = 42 + 32 = 25
|C| = √25 = 5 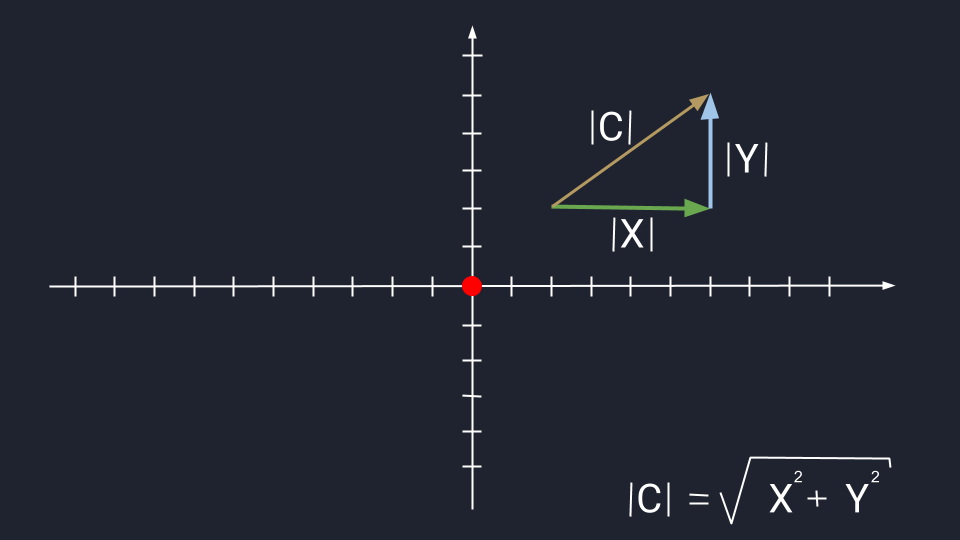
Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.
В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.
Умножение и деление вектора на число
Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.
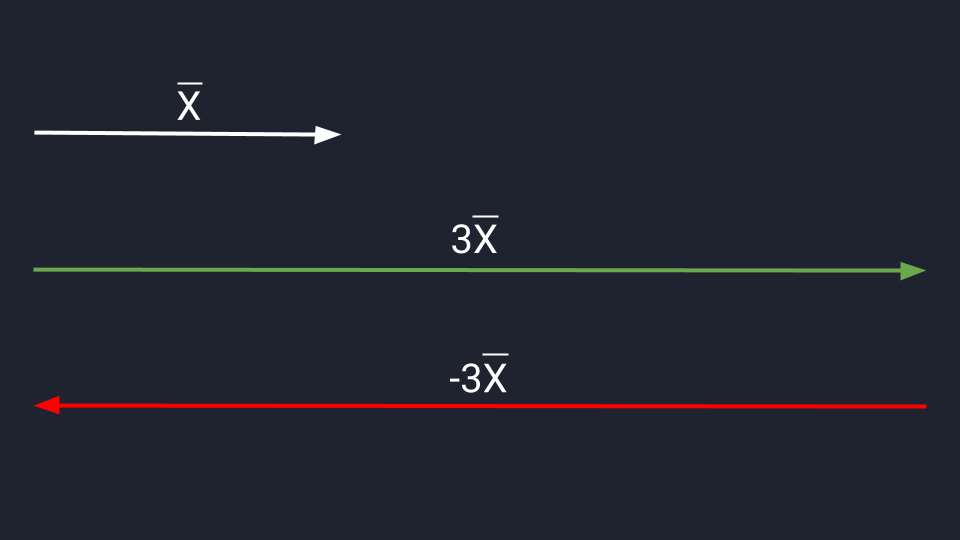
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.
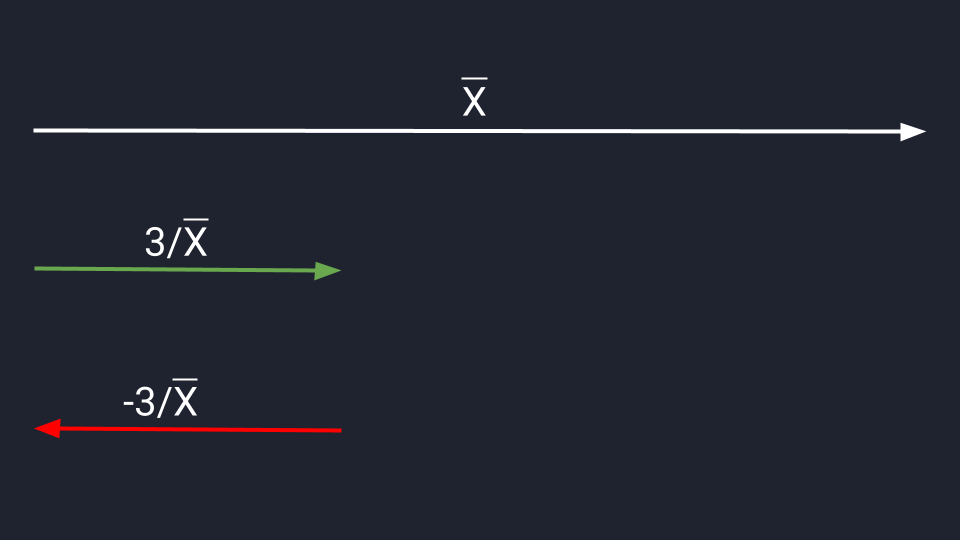
Да вроде несложно!
Пока ничего сложного. Но если углубляться, вы узнаете, что:
Что дальше
В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.
Векторы на ЕГЭ по математике. Действия над векторами
Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?
А в самом деле, что такое векторы и зачем они?
Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.
Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».
Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.
Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:
Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: 
До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.
Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.
Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.
Если координаты вектора заданы, его длина находится по формуле
Сложение векторов
Для сложения векторов есть два способа.
Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.
По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.
При сложении векторов 

Вычитание векторов
Вектор 



Теперь понятно, что такое вычитание векторов. Разность векторов 



Умножение вектора на число
При умножении вектора 



Скалярное произведение векторов
Векторы можно умножать не только на числа, но и друг на друга.
Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.
Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:
Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов 

Из формулы для скалярного произведения можно найти угол между векторами:
Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.
В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.
Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе.
 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»
— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.
Векторы для чайников. Действия с векторами.
Координаты вектора. Простейшие задачи с векторами
Наконец-то у меня добрались руки до обширной и долгожданной темы аналитической геометрии. Сначала немного о данном разделе высшей математики…. Наверняка вам сейчас вспомнился курс школьной геометрии с многочисленными теоремами, их доказательствами, чертежами и т.д. Что скрывать, нелюбимый и часто малопонятный предмет для значительной доли учеников. Аналитическая геометрия, как ни странно, может показаться более интересной и доступной. Что означает прилагательное «аналитическая»? На ум сразу приходят два штампованных математических оборота: «графический метод решения» и «аналитический метод решения». Графический метод, понятно, связан с построением графиков, чертежей. Аналитический же метод предполагает решение задач преимущественно посредством алгебраических действий. В этой связи алгоритм решений практически всех задач аналитической геометрии прост и прозрачен, зачастую достаточно аккуратно применить нужные формулы – и ответ готов! Нет, конечно, совсем без чертежей тут не обойдется, к тому же для лучшего понимания материала я постараюсь приводить их сверх необходимости.
Открываемый курс уроков по геометрии не претендует на теоретическую полноту, он ориентирован на решение практических задач. Я включу в свои лекции только то, что с моей точки зрения, является важным в практическом плане. Если вам необходима более полная справка по какому-либо подразделу, рекомендую следующую вполне доступную литературу:
1) Вещь, с которой, без шуток, знакомо несколько поколений: Школьный учебник по геометрии, авторы – Л.С. Атанасян и Компания. Сия вешалка школьной раздевалки уже выдержала 20 (!) переизданий, что, конечно, не является пределом.
2) Геометрия в 2 томах. Авторы Л.С. Атанасян, Базылев В.Т. Это литература для высшей школы, вам потребуется первый том. Из моего поля зрения могут выпадать редко встречающиеся задачи, и учебное пособие окажет неоценимую помощь.
Из инструментальных средств предлагаю собственную разработку – программный комплекс по аналитической геометрии, который значительно упростит жизнь и сэкономит массу времени.
Предполагается, что читатель знаком с базовыми геометрическими понятиями и фигурами: точка, прямая, плоскость, треугольник, параллелограмм, параллелепипед, куб и т.д. Желательно помнить некоторые теоремы, хотя бы теорему Пифагора, привет второгодникам)
А сейчас мы последовательно рассмотрим: понятие вектора, действия с векторами, координаты вектора. Далее рекомендую прочитать важнейшую статью Скалярное произведение векторов, а также Линейная (не) зависимость векторов. Базис векторов и Векторное и смешанное произведение векторов. Не лишней будет и локальная задача – Деление отрезка в данном отношении. На основе вышеуказанной информации можно освоить уравнение прямой на плоскости с простейшими примерами решений, что позволит научиться решать задачи по геометрии. Также полезны следующие статьи: Уравнение плоскости в пространстве, Уравнения прямой в пространстве, Основные задачи на прямую и плоскость, другие разделы аналитической геометрии. Естественно, попутно будут рассматриваться типовые задания.
Более того, по материалам сайта создана книга!
. да, это свершилось! – освойте азы теории и научитесь решать в кратчайшие сроки! Спасибо за поддержку проекта.
Понятие вектора. Свободный вектор
Сначала повторим школьное определение вектора. Вектором называется направленный отрезок, для которого указано его начало и конец: 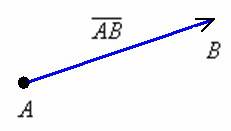
В данном случае началом отрезка является точка 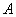
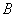
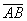
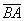
Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором 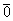
. Примечание: Здесь и далее можете считать, что векторы лежат в одной плоскости или можете считать, что они расположены в пространстве – суть излагаемого материала справедлива и для плоскости и для пространства.
Обозначения: Многие сразу обратили внимание на палочку без стрелочки в обозначении 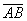
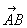
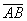
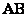
То была стилистика, а сейчас о способах записи векторов:
1) Векторы можно записать двумя большими латинскими буквами:
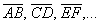
2) Векторы также записывают маленькими латинскими буквами:
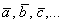
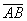
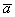
Длиной или модулем ненулевого вектора 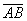
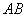
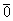
Длина вектора обозначается знаком модуля: 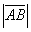
Как находить длину вектора мы узнаем (или повторим, для кого как) чуть позже.
То были элементарные сведения о векторе, знакомые всем школьникам. В аналитической же геометрии рассматривается так называемый свободный вектор.
Если совсем просто – вектор можно отложить от любой точки:
Такие векторы мы привыкли называть равными (определение равных векторов будет дано ниже), но чисто с математической точки зрения это ОДИН И ТОТ ЖЕ ВЕКТОР или свободный вектор. Почему свободный? Потому что в ходе решения задач вы можете «пристроить» тот или иной «школьный» вектор в ЛЮБУЮ, нужную вам точку плоскости или пространства. Это очень крутое свойство! Представьте направленный отрезок произвольной длины и направления – его можно «клонировать» бесконечное количество раз и в любой точке пространства, по сути, он существует ВЕЗДЕ. Есть такая студенческая присказка: Каждому лектору в ж**у по вектору. Ведь не просто остроумная рифма, всё почти корректно – направленный отрезок можно пристроить и туда. Но не спешите радоваться, чаще страдают сами студенты =)
Итак, свободный вектор – это множество одинаковых направленных отрезков. Школьное определение вектора, данное в начале параграфа: «Вектором называется направленный отрезок…», подразумевает конкретный направленный отрезок, взятый из данного множества, который привязан к определённой точке плоскости или пространства.
Далее, если не оговаривается иное, речь пойдёт только о свободных векторах.
Действия с векторами. Коллинеарность векторов
В школьном курсе геометрии рассматривается ряд действий и правил с векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др. Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.
Правило сложения векторов по правилу треугольников
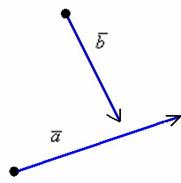
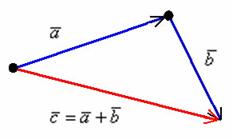
Рассмотрим два произвольных ненулевых вектора 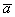
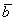
Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор 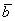
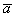
Суммой векторов 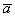
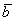
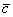
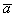
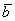
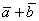
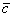
Кстати, если вектор 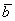
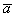
Умножение вектора на число
Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».
Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.
Обозначения: коллинеарность векторов записывают привычным значком параллельности: 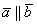
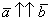
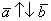
Произведением ненулевого вектора 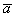
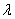
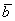
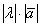
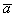
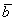
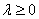
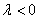
Правило умножения вектора на число легче понять с помощью рисунка:
Разбираемся более детально:
1) Направление. Если множитель 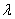
2) Длина. Если множитель заключен в пределах 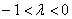
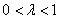
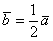
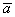
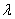
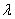
3) Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например, 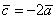
4) Векторы 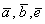
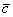
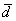
Какие векторы являются равными?
Два вектора равны, если они сонаправлены и имеют одинаковую длину. Заметьте, что сонаправленность подразумевает коллинеарность векторов. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».
С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.
Координаты вектора на плоскости и в пространстве
Первым пунктом рассмотрим векторы на плоскости. Изобразим декартову прямоугольную систему координат и от начала координат отложим единичные векторы 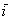
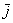
Векторы 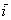
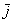
Обозначение: ортогональность векторов записывают привычным значком перпендикулярности, например: 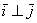
Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости. Что такое базис, думаю, интуитивно многим понятно, более подробную информацию можно найти в статье Линейная (не) зависимость векторов. Базис векторов. Простыми словами, базис и начало координат задают всю систему – это своеобразный фундамент, на котором кипит полная и насыщенная геометрическая жизнь.
Иногда построенный базис называют ортонормированным базисом плоскости: «орто» – потому что координатные векторы ортогональны, прилагательное «нормированный» означает единичный, т.е. длины векторов базиса равны единице.
Обозначение: базис обычно записывают в круглых скобках, внутри которых в строгой последовательности перечисляются базисные векторы, например: 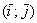
Любой вектор 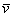
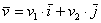
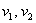
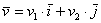
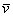
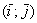
! ВСЕМ настоятельно рекомендую прочитать ВСЁ!
Начнем с первой буквы алфавита: 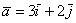
1) правило умножения вектора на число: 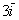
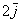
2) сложение векторов по правилу треугольника: 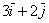
А теперь мысленно отложите вектор 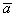
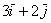
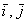
Векторы 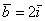
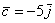
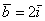
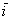
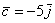
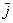
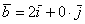
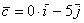
А базисные векторы, к слову, так: 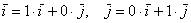
И, наконец: 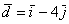
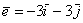
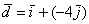
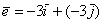
Рассмотренное разложение вида 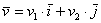
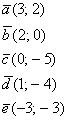
Сами базисные векторы записываются так: 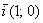
То есть, в круглых скобках указываются координаты вектора. В практических задачах используются все три варианта записи.
Сомневался, говорить ли, но всё-таки скажу: координаты векторов переставлять нельзя. Строго на первом месте записываем координату, которая соответствует единичному вектору 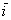
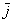
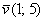
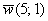
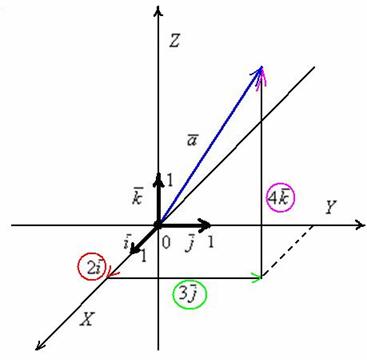
С координатами на плоскости разобрались. Теперь рассмотрим векторы в трехмерном пространстве, здесь практически всё так же! Только добавится ещё одна координата. Трехмерные чертежи выполнять тяжко, поэтому ограничусь одним вектором, который для простоты отложу от начала координат:
Перед вами ортонормированный базис 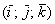
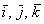
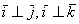
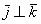
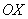
Любой вектор 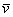
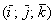
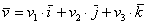
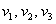
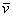
Пример с картинки: 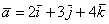
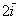
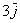
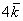
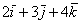
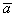
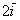
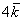
Все векторы трехмерного пространства, естественно, тоже свободны, попробуйте мысленно отложить вектор 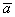
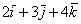
Аналогично плоскому случаю, помимо записи 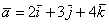
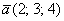
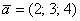
Если в разложении отсутствует один (или два) координатных вектора, то вместо них ставятся нули. Примеры:
вектор 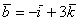
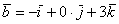
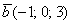
вектор 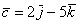
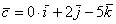
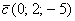
вектор 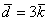
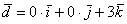
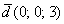
Базисные векторы записываются следующим образом:
Вот, пожалуй, и все минимальные теоретические знания, необходимые для решения задач аналитической геометрии. Возможно многовато терминов и определений, поэтому чайникам рекомендую перечитать и осмыслить данную информацию ещё раз. Да и любому читателю будет полезно время от времени обращаться к базовому уроку для лучшего усвоения материала. Коллинеарность, ортогональность, ортонормированный базис, разложение вектора – эти и другие понятия будут часто использоваться в дальнейшем. Отмечу, что материалов сайта недостаточно для сдачи теоретического зачета, коллоквиума по геометрии, так как все теоремы (к тому же без доказательств) я аккуратно шифрую – в ущерб научному стилю изложения, но плюсом к вашему пониманию предмета. Для получения обстоятельной теоретической справки прошу следовать на поклон к профессору Атанасяну.
А мы переходим к практической части:
Простейшие задачи аналитической геометрии.
Действия с векторами в координатах
Задания, которые будут рассмотрены, крайне желательно научиться решать на полном автомате, а формулы запомнить наизусть, даже специально не запоминать, сами запомнятся =) Это весьма важно, поскольку на простейших элементарных примерах базируются другие задачи аналитической геометрии, и будет досадно тратить дополнительное время на поедание пешек. Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.
Изложение материала пойдет параллельным курсом – и для плоскости, и для пространства. По той причине, что все формулы… сами увидите.
Как найти вектор по двум точкам?
Если даны две точки плоскости 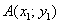
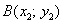
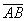
Если даны две точки пространства 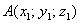
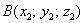
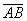
То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора.
Задание: Для тех же точек запишите формулы нахождения координат вектора 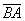
Даны две точки плоскости 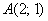
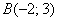
Решение: по соответствующей формуле:
Как вариант, можно было использовать следующую запись:
Эстеты решат и так:
Лично я привык к первой версии записи.
Ответ:
По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения некоторых моментов чайникам, не поленюсь:
Обязательно нужно понимать различие между координатами точек и координатами векторов:
Координаты точек – это обычные координаты в прямоугольной системе координат. Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.
Координаты же вектора – это его разложение по базису 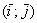
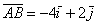
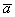
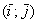
Записи координат точек и координат векторов вроде бы схожи: 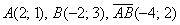
Дамы и господа, набиваем руку:
а) Даны точки 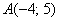
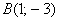
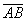
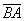
б) Даны точки 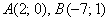
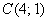
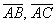
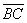
в) Даны точки 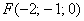
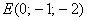
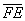
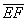
г) Даны точки 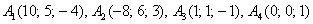
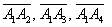
Пожалуй, достаточно. Это примеры для самостоятельного решения, постарайтесь ими не пренебрегать, окупится ;-). Чертежи делать не нужно. Решения и ответы в конце урока.
Что важно при решении задач аналитической геометрии? Важно быть ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫМ, чтобы не допустить мастерскую ошибку «два плюс два равно нулю». Сразу извиняюсь, если где ошибся =)
Как найти длину отрезка?
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости 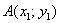
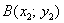
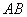
Если даны две точки пространства 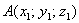
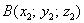
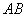
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: 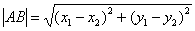
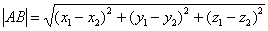
Даны точки 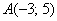
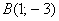
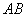
Решение: по соответствующей формуле:
Ответ:
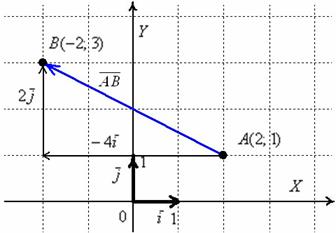
Для наглядности выполню чертёж
Отрезок 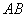
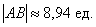
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём – вынесение множителя из-под корня. В результате вычислений у нас получился результат 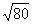
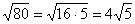
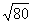
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например 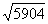
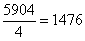
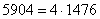
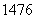
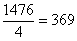
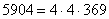
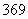
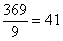
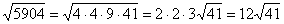
Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Даны точки 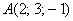
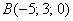
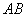
Решение и ответ в конце урока.
Как найти длину вектора?
Если дан вектор плоскости 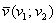
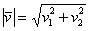
Если дан вектор пространства 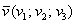
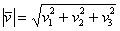
Данные формулы (как и формулы длины отрезка) легко выводятся с помощью небезызвестной теоремы Пифагора.
Даны точки 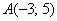
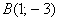
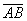
Я взял те же точки, что и в Примере 3.
Решение: Сначала найдём вектор 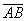
По формуле 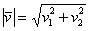
Ответ:
Не забываем указывать размерность – «единицы»! Всегда ли, кстати, нужно рассчитывать приближенное значение (в данном примере 8,94), если этого не требуется в условии? С моей точки зрения, лишним не будет, отсутствие приближенного значения тянет на придирку. Округление целесообразно проводить до 2-3 знаков после запятой.
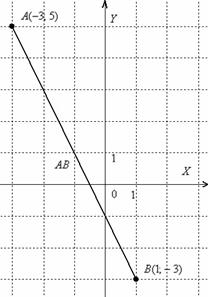
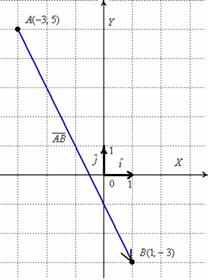
Выполним чертеж к задаче:
В чём принципиальное отличие от Примера 3? Отличие состоит в том, что здесь речь идёт о векторе, а не об отрезке. Вектор можно переместить в любую точку плоскости, при этом его лучше переобозначить, например, через 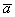
А в чём сходство Примера 3 и Примера 5? Геометрически очевидно, что длина отрезка 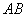
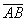
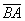
Задачу 3 можно было решить и вторым способом, повторю условие: Даны точки 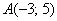
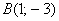
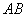
Вместо применения формулы 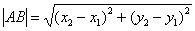
1) Находим вектор 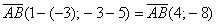
2) А теперь ссылаемся на то, что длина отрезка 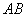
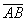
Этот способ широко практикуется в ходе решений задач аналитической геометрии.
Вышесказанное справедливо и для пространственного случая
а) Даны точки 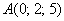
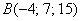
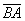
б) Даны векторы 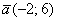
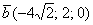
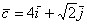
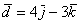
Решения и ответы в конце урока.
Действия с векторами в координатах
В первой части урока мы рассматривали правила сложения векторов и умножения вектора на число. Но рассматривали их с принципиально-графической точки зрения. Посмотрим, как данные правила работают аналитически – когда заданы координаты векторов:
1) Правило сложения векторов. Рассмотрим два вектора плоскости 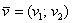
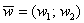
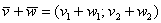
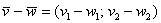
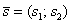
Если речь идёт о векторах в пространстве, то всё точно так же, только добавится дополнительная координата. Если даны векторы 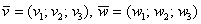
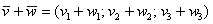
2) Правило умножения вектора на число. Ещё проще! Для того чтобы вектор 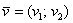
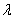
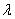
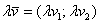
Для пространственного вектора 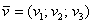
Приведённые факты строго доказываются в курсе аналитической геометрии.
Примечание: Данные правила справедливы не только для ортонормированных базисов 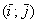
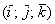
Даны векторы 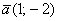
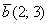
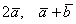
Решение чисто аналитическое:
Ответ:
Чертеж в подобных задачах строить не надо, тем не менее, геометрическая демонстрация будет весьма полезной. Если считать, что векторы заданы в ортонормированном базисе 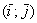
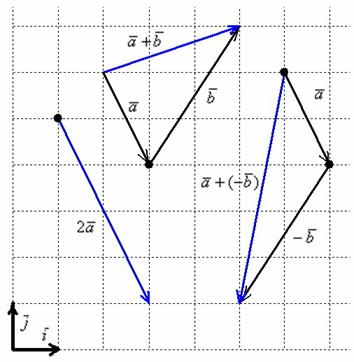
Коль скоро речь идет только о векторах в ортонормированном базисе, то оси рисовать не обязательно. Достаточно начертить базисные векторы, причём, где угодно. Ну, и координатную сетку для удобства. Строго говоря, ранее я допустил небольшой огрех – в некоторых чертежах урока тоже можно было не чертить декартову прямоугольную систему координат. Векторам она не нужна, им нужен базис. Впрочем, лучше всегда рисуйте, а то напугаете всех своими знаниями =)
Как видите, графический способ решения привёл к тем же результатам, что и аналитический способ решения. Ещё раз заметьте свободу векторов: любую из трёх «конструкций» можно переместить в любую точку плоскости.
Для векторов в пространстве можно провести аналогичные выкладки. Но там чертежи строить значительно сложнее, поэтому ограничусь аналитическим решением (на практике, собственно, бОльшего и не надо):
Даны векторы 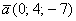
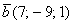
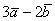
Решение: Для действий с векторами справедлив обычный алгебраический приоритет: сначала умножаем, потом складываем:
Ответ:
И в заключение занятный пример с векторами на плоскости:
Даны векторы 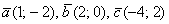
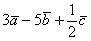
Это задача для самостоятельного решения.
Какой вывод? Многие задачи аналитической геометрии прозрачны и просты, главное, не допустить вычислительных ошибок. Следующие рекомендуемые к изучению уроки:
Это, так скажем, вектор-минимум студента =)
Любите векторы, и векторы полюбят вас!
Задание: 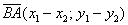
Пример 2: Решение:
а) 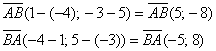
б) 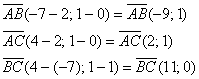
в) 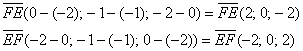
г)
Пример 4: Решение:
По соответствующей формуле: 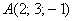
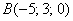
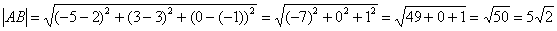
Ответ:
Пример 6: 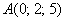
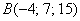
а) Решение: найдём вектор 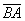
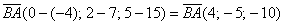
Вычислим длину вектора: 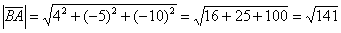
Ответ:
б) Решение:
Вычислим длины векторов:
Пример 9: Решение: 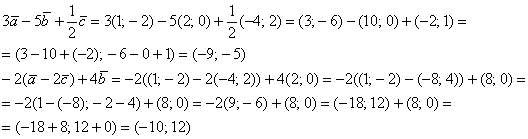
Примечание: Перед выполнением действий можно предварительно раскрыть скобки:
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5














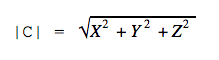
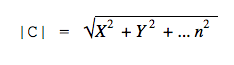

















 Онлайн-курс «Математика 10+11 100 баллов»
Онлайн-курс «Математика 10+11 100 баллов»