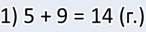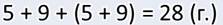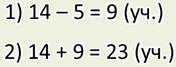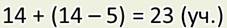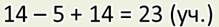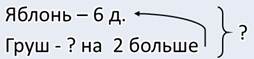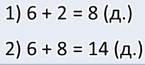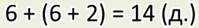Что значит решить задачу по действиям и выражением

Различные способы решения задач и различные формы записи решения

Страницы работы

Содержание работы

На одном из уроков математики во II клас­се ученик, получив задание “Реши задачу”, спросил: “Каким способом нужно решать: по действиям или выражением”. Учитель ответил: “По действиям”.

Этот диалог показал, что и учитель, и уче­ник принимают различные формы запи­си решения за различные способы ее решения. Посещение уроков, беседы с учителями и учащимися позволили нам сде­лать вывод, что эта ошибка довольно распро­странена. Смешение же названных понятий приводит к тому, что, когда требуется дей­ствительно решить задачу разными способами, учащиеся либо вовсе не понимают задания, либо понимают его с большим трудом. А это, в свою очередь, снижает обучающие и воспитывающие возможности такого важного вида работы над задачей, как решение задач раз­ными способами.

Поэтому мы считаем своевременным обра­тить внимание учителей на отличие понятий способа решения задачи и формы записи решения задачи.

Задача считается решенной различными спо­собами, если се решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью использования этих связей.

Рассмотрим, например, задачу № 522 из учебника математики для II класса: “Для уро­ков труда купили 4 катушки белых ниток, по 10 коп. за катушку, и 6 катушек черных ни­ток по такой же цене. Сколько денег уплатили за эти нитки?”

Эта задача может быть решена двумя ариф­метическими способами.

При первом из них, наиболее очевидном, первоначально определяют стоимость черных ниток: (10-4)-коп., затем стоимость белых ни­ток: (10-6) коп. и, наконец, стоимость всех ниток.

При втором способе замечаем, что цена 1 катушки белых ниток та же, что и черных, поэтому вначале можно узнать, сколько всего катушек ниток купили (6+4), а затем опре­делить стоимость всех этих ниток

Запись решения, для каждого способа может быть выполнена в нескольких формах. Пока­жем все эти формы для каждого способа ре­шения.

Запись решения по действиям с пла­ном.

1. Сколько стоят белые нитки? 10·4 = 40 (коп.)

2. Сколько стоят черные нитки? 10·6=60 (коп.)

3. Сколько денег уплатили за все эти нитки?

1. Сколько всего катушек с нитками купили?

2. Сколько денег уплатили за все эти нитки?

В настоящее время эта форма записи реше­ния задач в начальной школе практически не применяется. Однако мы считаем, что озна­комить с ней учащихся полезно и ее можно использовать на уроках математики, хотя и значительно реже, чем другие формы.

Рассмотрим другую форму записи решения той же задачи — это запись решения по дей­ствиям с пояснениями.

1. 10 · 4 =40 (коп) — стоимость белых ниток,

2. 10 ·6 = 60 (коп) — стоимость черных ни­ток.

3. 40+60=100 (коп.) — стоимость всех ни­ток.

1. 6+4 = 10 (шт.) — всего купили катушек ниток.

2. 10·10 = 100 (коп) — стоимость всех ниток.

Решение задачи можно также оформить по действиям без пояснений.

Ответ: все нитки стоят 1 руб.

Ответ: все нитки стоят 1 руб.

По задаче можно также составить выражение и найти его значение.

Ответ: все нитки стоят 1 руб

Ответ: все нитки стоят 1 руб.

Запись решения в этой форме осуществляется учащимися в два этапа. Вначале составляется выражение, затем учащиеся находят его значение, после чего запись решения приобретает вид равенства, в левой части кото­рого записано выражение, составленное по задаче, а в правой части — его значение.

Ни в коем случае нельзя называть запись 10 · 4 + 10 · 6 = 100 выражением, так как это противоречит тому определению поня­тия выражения, которое положено в основу изучения этого понятия в школе. Математи­ческое выражение составляется из цифр, букв, знаков арифметических действий и скобок, но не содержит знаков математических отноше­ний: равенства, неравенства и др. Два мате­матических выражения, соединенные знаком равенства, образуют равенство.

Приведенная выше запись — это равенство, левая часть которого есть выражение, составленное по задаче (10 · 4 + 10 ··6), а правая часть — выражение, состоящее всего лишь из одного числа (100), являющегося значением предыдущего выражения.

При проверке решения задачи, записанной в этой форме, учащимся можно дать такие задания:

1. Прочитайте выражение, составленное по задаче.

2. Назовите значение этого выражения. (Значение составленного по задаче выражения равно 100.)

3. Дайте ответ на вопрос задачи. (Все нитки стоят 100 коп., т. е. 1 руб.)

При решении задач следует правильно употреблять в своей речи соответствующие термины: Решите задачу и запишите решение по действиям с пояснениями. Решите задачу двумя способами, записав каждое решение в виде равенства, левая часть которого — выражение, составленное по задаче. Решите задачу двумя способами. Составьте соответствующие выражения и найдите их значения. Решите задачу и запишите решение вначале по действиям с пояснениями, а затем в виде выражения. Найдите значение этого выражения. Дайте ответ на вопрос задачи.

Источник

Запись решения задачи выражением

Урок 15. Математика 2 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Запись решения задачи выражением»

— Плюс. Плююююс! Ты где?

Привет, Плюс! Чего так долго? Включай скорее компьютер. Сейчас у нас будет в скайпе разговор с царицей Математикой.

— Здравствуй, Минус. Как это я забыл! Включаю.

— Здравствуйте, Дорогие Плюс и Минус!

— Да, царица, мы Вас внимательно слушаем.

— Мы очень внимательно слушаем.

— Ну что же, приступим. Итак, вот первая задача:

Ну, Плюс и Минус, я жду вашего решения. Может быть и ребята, которые на вас смотрят, попробуют решить эту задачу.

— Всё, я готов! Могу даже объяснить, как я решал эту задачу.

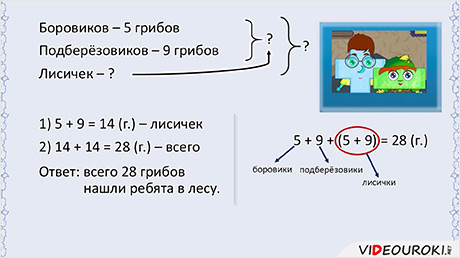
В задаче два неизвестных, значит, задача составная, то есть в ней не одно действие, а два. В первом действии я узнаю, сколько лисичек.

А так как боровиков и подберёзовиков вместе столько же, сколько и лисичек, то общее количество грибов я нашёл вот так:

Ответ: всего 28 грибов нашли ребята в лесу.

— А я решал задачу другим способом. Вот посмотрите:

— Ну что же, начинаем решать. Ребята, и вы попробуйте с нами решать!

— Я уже решил. Вот посмотрите, в задаче известно количество мальчиков, Их 14. Но неизвестно количество девочек. Ведь сказано, что их на 5 меньше, чем мальчиков.

Ответ: всего 23 учащихся присутствовало на уроке физкультуры.

— А вот я записал решение этой задачи по-другому:

И ещё можно вот так:

Ты первым действием узнаёшь, сколько девочек, и я тоже. Ведь это действие я записал в скобках. А то, что записано в скобках, всегда выполняется первым.

— Ты, Плюс, как всегда. Все тебе надо складывать да экономить. Хотя, наверное, ты прав. Эта запись действительно удобная. А хотелось бы и мне попробовать такую запись задачи выражением.

Ваше величество, госпожа королева. Не могли бы Вы задать нам ещё одну задачу?

— Ну что же, слушайте:

В моём саду растёт 6 яблонь. А груш на 2больше. Сколько всего яблонь и груш растёт в моём саду?

— Ну вот что у меня получилось. Прежде, чем узнать, сколько всего яблонь и груш, необходимо узнать, сколько груш. Ведь нам это неизвестно. Сказано, что их на 2 больше, чем яблонь.

Значит, в саду царицы растёт 14 яблонь и груш.

А вот как получилась запись выражением:

— Хорошо. Задача решена, верно. А теперь расскажите, чему вы научились.

— Можно я начну первый.

Записывать решение задачи можно по действиям и выражением.

— При записи по действиям мы пишем номер действия и пояснения к каждому действию, а при записи выражением только пояснение к значению записанного выражения.

— При записи выражения первое действие часто записываем в скобках, и конечно, не забываем записать ответ задачи.

— Ну что же, молодцы, Плюс и Минус. Вы справились с заданием. И сейчас вы можете пойти погулять в мой сад и полакомиться яблоками и грушами.

Источник

Математика. 2 класс

Конспект урока

Математика, 2 класс

Урок № 22. Решение текстовых задач. Запись решения выражением

Перечень вопросов, рассматриваемых в теме:

— Что такое встречное движение, расстояние?

— Как выполнять схематический чертёж к задачам на движение?

Задача – это упражнение, которое выполняется посредством умозаключения, вычисления.

Выражение – формула, выражающая какие–либо математические отношения.

Расстояние – пространственный промежуток, разделяющий два объекта, отрезок пути.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

Теоретический материал для самостоятельного изучения

Расстояние – это путь, который прошёл какой-либо объект.

РАССТОЯНИЕ – промежуток в пространстве, разделяющий два объекта

Измеряя расстояние, мы будем использовать сокращённые записи.

Сегодня на уроке мы будем решать новые задачи – задачи на движение.

Длина аллеи 80 м. Два мальчика пошли навстречу друг другу. Один прошёл до встречи 45 м. Сколько прошёл до встречи другой мальчик?

Сделаем к задаче схематический чертёж.

Начертим отрезок, обозначающий длину всей дорожки, или расстояние между концами дорожки. Синей стрелкой обозначим длину дорожки. Укажем – 80 метров.

Мальчики шли навстречу друг другу с разных сторон дорожки. На чертеже это будем обозначать стрелками, которые показывают направление движения каждого мальчика.

Место встречи мальчиков будем обозначать флажком.

Теперь обозначим, что один мальчик прошёл до встречи 45 метров, а другой –

неизвестно. Поставим знак вопроса.

Так выглядит схематический чертёж к задаче. По чертежу видно, что нам необходимо найти разность отрезков, выполнить вычитание.

Чтобы узнать, сколько метров до встречи прошёл второй мальчик, вычтем из длины всей дорожки длину пути, который прошёл первый мальчик.

80 – 45 = 35 (м) прошёл второй мальчик.

Второй мальчик прошёл до встречи 35 метров.

Решим вторую задачу:

Девочки измеряли длину дорожки с двух концов, идя навстречу друг другу. Одна девочка прошла до встречи 30 м, другая на 4 метра меньше. Какой длины была дорожка?

Сделаем схематический чертёж к задаче.

Итак, нам надо найти длину всей дорожки. Для этого мы должны знать, сколько метров прошла каждая девочка. Мы знаем, сколько прошла первая девочка – 30 метров. А сколько прошла вторая девочка, нам надо узнать.

Будем решать задачу в два действия. Запишем первое действие:

1) 30 – 4 = 26 (м) прошла вторая девочка.

Вторая девочка прошла до встречи двадцать шесть метров.

Теперь можем ответить на вопрос задачи. Запишем второе действие:

2) 30 + 26 = 56 (м) длина дорожки.

Длина всей дорожки была 56 метров.

Вывод: Для решения задач на движение обычно выполняют чертёж, в котором стрелками показывают направление движения объектов. Движение может быть встречным или в противоположных направлениях.

1.Подберите схематический чертёж к задаче

Красная Шапочка отправилась в гости к бабушке. До дома бабушки нужно пройти 100 метров. Красная Шапочка уже прошла 70 метров. Сколько ей осталось пройти?

2.Соедините каждый чертёж с карточкой, на которой записано соответствующее решение задачи.

30 – 20

30 + 20

70 – 45

70 – 45

30 + 20

30 – 20

Источник

Порядок выполнения действий, правила, примеры

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Порядок вычисления простых выражений

В случае выражений без скобок порядок действий определяется однозначно:

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Решение

17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

.

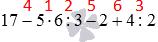
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Решение

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Решение

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Решение

Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.

( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Источник

Правила выполнения математических действий

Основные операции в математике

Основными действиями являются:

Наряду с этими операциями предусмотрены отношения:

Сложение является операцией для объединения пары слагаемых.

Сложение записывают таким образом:

5, 1 — слагаемые, 6 — сумма.

Вычитание — операция, которая является обратным действием сложению.

Записывать вычитание следует таким образом:

10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

При сложении разности в виде 9 и вычитаемого в виде 1 можно получить 10, которое является уменьшаемым. Сложение можно проверить вычитанием:

Умножение является действием в арифметике и имеет вид сокращенной записи сложения идентичных слагаемых.

В данном случае 3 — множимое, 4 — множитель, 12 — произведение.

Множимое и множитель можно поменять местами. При этом произведение не поменяется:

В связи с этим, множитель и множимое являются сомножителями.

Деление — арифметическая операция, которая является обратным действием умножению.

Деление, в том числе для многочленов, записывают таким образом:

При умножении делителя на частное получаем делимое, то есть:

В некоторых уравнениях можно встретить на месте частного не целое число. В таком случае его допустимо записать в виде дроби.

Возведение в степень является действием умножения числа на самого себя несколько раз.

Основанием степени является число, повторяющееся сомножителем конкретное количество раз. Роль показателя степени играет число, указывающее на то количество раз, которое берется одинаковый множитель. Степень — число, являющееся результатом взаимодействия основания и показателя степени.

Здесь 3 является основанием степени, 4 определяется, как показатель степени, 81 называют степенью.

Вторая степень — квадрат, а третья степень — куб. Первая степень числа является самим числом.

В данном случае 81 является подкоренным числом, 4 — показатель корня, 3 — корень.

С целью проверки операции по извлечению корня можно возвести 3 в степень 4, что в результате дает 81:

Квадратный корень — это корень второй степени:

Если предполагается запись квадратного корня, то показатель корня допускается не записывать:

Кубический корень — это корень третьей степени:

Сложение является обратным действием вычитанию, умножение — делению, возведение в степень — извлечению корня, и наоборот.

Порядок вычисления простых выражений

Перед решением простых уравнений полезно ознакомиться с последовательностью действий:

Рассмотреть это правило можно на практике.

Нужно решить письменное уравнение:

В первую очередь следует проверить, есть ли скобки для группировки элементов выражения. Здесь они отсутствуют, как и операции умножения и деления. Тогда можно выполнять действия, руководствуясь стандартным алгоритмом, описанным выше: витаем 2 из 11, складываем остаток с 5, в результате получим 14.

11 – 2 + 5 = 9 + 5 = 14

Скобки в данном примере отсутствуют, но имеются операции деления и умножения. При их обнаружении нужно с помощью правила последовательно выполнять действия, двигаясь слева направо: 10 делим на 2, полученное число умножаем на 7, результат делим на 5.

10 ÷ 2 × 7 ÷ 5 = 5 × 7 ÷ 5 = 35 ÷ 5 = 7

В процессе изучения данной темы, пока опыта еще не достаточно, полезно расставлять над знаками арифметических операций цифры в порядке их выполнения. Такая работа значительно упрощает вычисления и исключает ошибки.

Что такое действия первой и второй ступени

В учебной литературе по математике можно встретить такие понятия, как действие первой и второй ступени:

В том случае, когда в выражении отсутствуют скобки, операции выполняются в следующем порядке:

Порядок вычислений в выражениях со скобками

Наличие в выражении скобок изменяет стандартный алгоритм арифметических операций. Это своеобразный индикатор для действий, которые должны быть выполнены в первую очередь.

В первую очередь следует выполнить операции, заключенные в скобках. При этом важно соблюдать стандартный порядок действий, то есть слева направо умножать и делить, а далее — складывать и вычитать.

Выражения, заключенные в скобках, являются составными компонентами начального выражения. Для таких выражений стандартный алгоритм действий остается без изменений. Рассмотреть вычисления можно на практических примерах.

Так как в выражении есть скобки, в первую очередь нужно выполнить действия в этих скобках:

Руководствуясь стандартным алгоритмом, сначала умножаем, затем — вычитаем:

Перейдем ко второму выражению, заключенному в скобках:

Так как в данном случае имеется лишь вычитание, выполняем действие:

Результаты, которые получили при решении выражений в скобках, следует подставить в начальное выражение:

Сначала нужно умножить, затем поделить, а далее выполнить сложение:

10 + 2 × 8 ÷ 2 = 10 + 16 ÷ 2 = 10 + 8 = 18

Порядок действий в выражениях без скобок

В данном случае присутствуют действия сложения и вычитания, которые следует выполнять по порядку, двигаясь слева направо.

Здесь умножение и деление. Данные арифметические операции также выполняем по порядку, начиная с левой стороны, двигаясь в правую сторону.

Когда выражения содержат операции сложение и вычитание, либо деление и умножение, то вычисления нужно выполнять по порядку слева направо.

Нередко встречаются примеры, где есть сложение и вычитание, а также умножение и деление. Тогда в первую очередь делят и умножают по порядку, а на втором этапе складывают и вычитают также в определенном порядке.

Решение примеров

Согласно стандартному алгоритму, проверяем наличие скобок. Так как скобки имеются, начинаем с них:

Полученный результат следует подставить в исходное выражение:

Скобки отсутствуют, но есть умножение, которое необходимо выполнить в первую очередь:

Подставим результат в начальное выражение:

Решим полученное выражение:

Если сразу обозначить порядок действий, то запись примет вид:

Источник