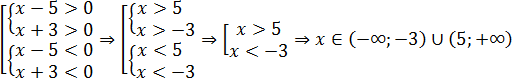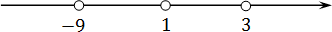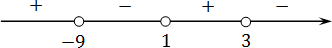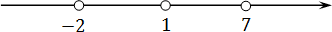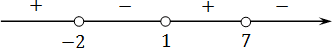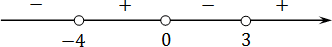Что значит решить методом интервалов неравенство
Метод интервалов
теория по математике 📈 неравенства
Методом интервалов решают неравенства вида:
Для решения данного вида неравенств используется свойство чередования знаков функции f(x)=(х – х1)(х – х2)….(х – хn), где числа х1, х2, …, хn называются нулями функции. Эти нули функции разбивают область определения (она представляет собой любое число, т.е. промежуток чисел от минус бесконечности до плюс бесконечности) на промежутки, в каждом из которых знак функции сохраняется, а при переходе через нуль ее знак изменяется. Данные промежутки называют интервалами, а решение неравенств данным способом – методом интервалов.
Для начала решения неравенство должно быть представлено в стандартном виде. Рассмотрим решение такого вида неравенств методом интервалов на примерах.
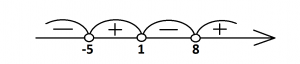
Пример №1. Решить неравенство:
Найдем нули функции: для этого возьмем из каждой скобки данные числа с противоположными знаками, поэтому имеем х1=1, х2=–5, х3=8. Данные числа разбивают область определения на промежутки (−∞;−5);(−5;1);(1;8);(8;+∞). Удобно показать их на координатном луче, помня о том, что неравенство по условию строгое, значит, точки будут «выколотые»:
Теперь посмотрим, как расставить знаки в промежутках. Начнем справа, возьмем из этого промежутка любое число, например, 9 и подставим его в наше неравенство:
то есть получили, что произведение – положительное число, поэтому ставим знак «плюс»; теперь берем число из промежутка (1;8), например, 5 и также подставим в неравенство для определения знака произведения:
Пример №2. Решить неравенство:
В данном случае мы видим, что есть отличие от неравенства стандартного вида. Но помним, что в случае сложения или вычитания переменной х и нуля мы получим переменную х, т.е. неравенство могло выглядеть так:
Значит, одним из нулей функции будет число нуль. Итак, имеем нули функции 0 и 6. Ставим их на числовом луче, помня о том, что точки будут «приколотые», расставляем знаки путем чередования справа налево:
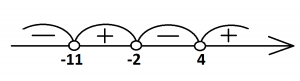
Именно это неравенство будем решать. Итак, нули функции – это –11, 4 и –2. Расставляем их на числовом луче и расставляем знаки путем чередования, получим:
Ищем промежутки, соответствующие неравенству стандартного вида, к которому мы привели, т.е. для (х+11)(х – 4)(x+2)>0.
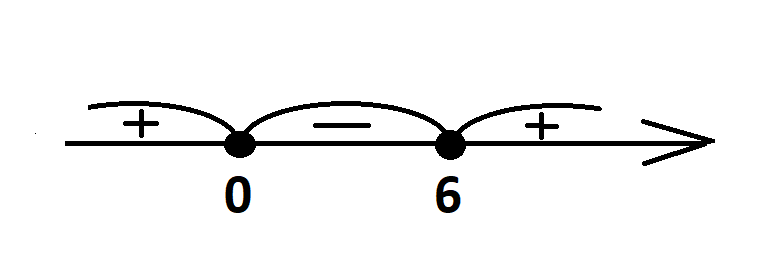
Найдем нули функции, приравняв каждый множитель к нулю: х=0 и х – 8=0, найдем х из второго уравнения: х=8.
Итак, имеем нули функции 0 и 8.
Теперь расставляем их на числовом луче и решаем неравенство методом интервалов.
Теперь находим промежуток чисел, соответствующий неравенству х(х – 8) ≤ 0, т.е. промежуток отрицательных или равных нулю чисел. Это будет промежуток [0; 8]
В соответствии с его номером, это будет ответ под №3.
pазбирался: Даниил Романович | обсудить разбор | оценить
Метод интервалов: решение простейших строгих неравенств
Для начала — немного лирики, чтобы почувствовать проблему, которую решает метод интервалов. Допустим, нам надо решить вот такое неравенство:
Какие есть варианты? Первое, что приходит в голову большинству учеников — это правила «плюс на плюс дает плюс» и «минус на минус дает плюс». Поэтому достаточно рассмотреть случай, когда обе скобки положительны: x − 5 > 0 и x + 3 > 0. Затем также рассмотрим случай, когда обе скобки отрицательны: x − 5 x + 3
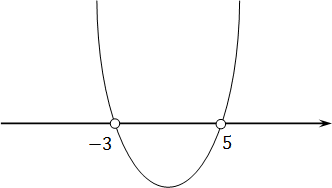
Более продвинутые ученики вспомнят (может быть), что слева стоит квадратичная функция, график которой — парабола. Причем эта парабола пересекает ось OX в точках x = 5 и x = −3. Для дальнейшей работы надо раскрыть скобки. Имеем:
Теперь понятно, что ветви параболы направлены вверх, т.к. коэффициент a = 1 > 0. Попробуем нарисовать схему этой параболы:
Обратите внимание: на рисунке изображена именно схема функции, а не ее график. Потому что для настоящего графика надо считать координаты, рассчитывать смещения и прочую хрень, которая нам сейчас совершенно ни к чему.
Почему эти методы неэффективны?
Итак, мы рассмотрели два решения одного и того же неравенства. Оба они оказались весьма громоздкими. В первом решении возникает — вы только вдумайтесь! — совокупность систем неравенств. Второе решение тоже не особо легкое: нужно помнить график параболы и еще кучу мелких фактов.
Это было очень простое неравенство. В нем всего 2 множителя. А теперь представьте, что множителей будет не 2, а хотя бы 4. Например:
Вот и все! После этого останется лишь выписать интервалы, которые нас интересуют. Они отмечены знаком «+», если неравенство имело вид f ( x ) > 0, или знаком «−», если неравенство имеет вид f ( x ) x − 2)( x + 7) x − 2)( x + 7) = 0
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю:
x − 2 = 0 ⇒ x = 2;
x + 7 = 0 ⇒ x = −7.
Получили два корня. Переходим к шагу 2: отмечаем эти корни на координатной прямой. Имеем:
Теперь шаг 3: находим знак функции на самом правом интервале (правее отмеченной точки x = 2). Для этого надо взять любое число, которое больше числа x = 2. Например, возьмем x = 3 (но никто не запрещает взять x = 4, x = 10 и даже x = 10 000). Получим:
f ( x ) = ( x − 2)( x + 7);
x = 3;
f (3) = (3 − 2)(3 + 7) = 1 · 10 = 10;
Получаем, что f (3) = 10 > 0, поэтому в самом правом интервале ставим знак плюс.
Переходим к последнему пункту — надо отметить знаки на остальных интервалах. Помним, что при переходе через каждый корень знак должен меняться. Например, справа от корня x = 2 стоит плюс (мы убедились в этом на предыдущем шаге), поэтому слева обязан стоять минус.
Этот минус распространяется на весь интервал (−7; 2), поэтому справа от корня x = −7 стоит минус. Следовательно, слева от корня x = −7 стоит плюс. Осталось отметить эти знаки на координатной оси. Имеем:
Вернемся к исходному неравенству, которое имело вид:
( x − 2)( x + 7) x + 9)( x − 3)(1 − x ) x + 9)( x − 3)(1 − x ) = 0;
x + 9 = 0 ⇒ x = −9;
x − 3 = 0 ⇒ x = 3;
1 − x = 0 ⇒ x = 1.
Помните: произведение равно нулю, когда хотя бы один из множителей равен нулю. Именно поэтому мы вправе приравнять к нулю каждую отдельную скобку.
Шаг 2: отмечаем все корни на координатной прямой:
Шаг 3: выясняем знак самого правого промежутка. Берем любое число, которое больше, чем x = 1. Например, можно взять x = 10. Имеем:
f ( x ) = ( x + 9)( x − 3)(1 − x );
x = 10;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197;
f (10) = −1197
Вот и все. Осталось лишь выписать ответ. Взгляните еще раз на исходное неравенство:
( x + 9)( x − 3)(1 − x ) f ( x ) x ∈ (−9; 1) ∪ (3; +∞)
Замечание по поводу знаков функции
Практика показывает, что наибольшие трудности в методе интервалов возникают на последних двух шагах, т.е. при расстановке знаков. Многие ученики начинают путаться: какие надо брать числа и где ставить знаки.
Чтобы окончательно разобраться в методе интервалов, рассмотрим два замечания, на которых он построен:
Вот и все, что нужно знать про метод интервалов. Конечно, мы разобрали его в самом простом варианте. Существуют более сложные неравенства — нестрогие, дробные и с повторяющимися корнями. Для них тоже можно применять метод интервалов, но это тема для отдельного большого урока.
Теперь хотел бы разобрать продвинутый прием, который резко упрощает метод интервалов. Точнее, упрощение затрагивает только третий шаг — вычисление знака на самом правом куске прямой. По каким-то причинам этот прием не проходят в школах (по крайней мере, мне никто такого не объяснял). А зря — ведь на самом деле этот алгоритм очень прост.
( x − 1)(2 + x )(7 − x ) f ( x ) = ( x − 1)(2 + x )(7 − x );
( x − 1)(2 + x )(7 − x ) = 0;
x − 1 = 0 ⇒ x = 1;
2 + x = 0 ⇒ x = −2;
7 − x = 0 ⇒ x = 7;
Мы получили 3 корня. Перечислим их в порядке возрастания: x = −2, x = 1 и x = 7. Очевидно, что наибольший корень — это x = 7.
Для тех, кому легче рассуждать графически, я отмечу эти корни на координатной прямой. Посмотрим, что получится:
Требуется найти знак функции f ( x ) на самом правом интервале, т.е. на (7; +∞). Но как мы уже отмечали, для определения знака можно взять любое число из этого интервала. Например, можно взять x = 8, x = 150 и т.д. А теперь — тот самый прием, который не проходят в школах: давайте в качестве числа возьмем бесконечность. Точнее, плюс бесконечность, т.е. +∞.
«Ты че, обкурился? Как можно подставить в функцию бесконечность?» — возможно, спросите вы. Но задумайтесь: нам ведь не нужно само значение функции, нам нужен только знак. Поэтому, например, значения f ( x ) = −1 и f ( x ) = −938 740 576 215 значат одно и то же: функция на данном интервале отрицательна. Поэтому все, что от вас требуется — найти знак, который возникает на бесконечности, а не значение функции.
На самом деле, подставлять бесконечность очень просто. Вернемся к нашей функции:
f ( x ) = ( x − 1)(2 + x )(7 − x )
Представьте, что x — это очень большое число. Миллиард или даже триллион. Теперь посмотрим, что будет происходить в каждой скобке.
Первая скобка: ( x − 1). Что будет, если из миллиарда вычесть единицу? Получится число, не особо отличающееся от миллиарда, и это число будет положительным. Аналогично со второй скобкой: (2 + x ). Если к двойке прибавить миллиард, по получим миллиард с копейками — это положительное число. Наконец, третья скобка: (7 − x ). Здесь будет минус миллиард, от которого «отгрызли» жалкий кусочек в виде семерки. Т.е. полученное число мало чем будет отличаться от минус миллиарда — оно будет отрицательным.
Осталось найти знак всего произведения. Поскольку в первых скобках у нас был плюс, а в последней — минус, получаем следующую конструкцию:
Итоговый знак — минус! И неважно, чему равно значение самой функции. Главное, что это значение — отрицательное, т.е. на самом правом интервале стоит знак минус. Осталось выполнить четвертый шаг метода интервалов: расставить все знаки. Имеем:
Исходное неравенство имело вид:
( x − 1)(2 + x )(7 − x ) x ∈ (−2; 1) ∪ (7; +∞)
Вот и весь прием, который я хотел рассказать. В заключение — еще одно неравенство, которое решается методом интервалов с привлечением бесконечности. Чтобы визуально сократить решение, я не буду писать номера шагов и развернутые комментарии. Напишу только то, что действительно надо писать при решении реальных задач:
Заменяем неравенство уравнением и решаем его:
x (2 x + 8)( x − 3) = 0;
x = 0;
2 x + 8 = 0 ⇒ x = −4;
x − 3 = 0 ⇒ x = 3.
Отмечаем все три корня на координатной прямой (сразу со знаками):
Справа на координатной оси стоит плюс, т.к. функция имеет вид:
f ( x ) = x (2 x + 8)( x − 3)
А если подставить бесконечность (например, миллиард), получим три положительных скобки. Поскольку исходное выражение должно быть больше нуля, нас интересуют только плюсы. Осталось выписать ответ:
Метод интервалов
Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.
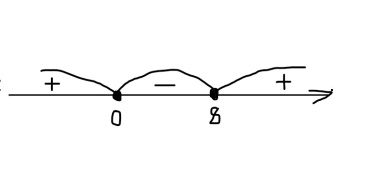
1. Рассмотрим, например, такое неравенство
Метод интервалов позволяет решить его за пару минут.
В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.
Метод интервалов основан на следующем свойстве дробно-рациональной функции.
Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.
Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).
Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.
Эти точки разбивают ось на промежутков.
При левая часть неравенства отрицательна.
Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:
Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.
Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:
Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.
Ты нашел то, что искал? Поделись с друзьями!
2. Рассмотрим еще одно неравенство.
При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак :
При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак :
Наконец, при 3′ alt=’x>3′ /> все множители положительны, и левая часть имеет знак :
Почему нарушилось чередование знаков? Потому что при переходе через точку «ответственный» за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.
Вывод: если линейный множитель стоит в чётной степени (например, в квадрате), то при переходе через точку знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.
3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:
Левая часть та же, что и в предыдущей задаче. Та же будет и картина знаков:
В задаче на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:
— которое легко решается методом интервалов.
5. Рассмотрим еще одно неравенство, на вид совсем простое:
Мы поступим по другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:
Метод интервалов (ЕГЭ 2022)
Метод интервалов тебе просто необходимо понять и знать его как свои пять пальцев!
Хотя бы потому, что он применяется для решения рациональных неравенств.
И потому, что, зная этот метод как следует, решать эти неравенства на удивление просто.
Чуть позже раскрою тебе пару секретов, как сэкономить время на решении этих неравенств.
Ну что, заинтриговал? Тогда поехали!
Метод интервалов — коротко о главном
Метод интервалов применяется для решения рациональных неравенств.
Он заключается в определении знака произведения по знакам сомножителей на различных промежутках.
Алгоритм решения рациональных неравенств методом интервалов:
Суть метода интервалов
Суть метода в разложении неравенства на множители (повтори тему «Разложение на множители»), определении ОДЗ и знака сомножителей.
Возьмем самый простенький пример: \( (x+1)\cdot (
Области допустимых значений (ОДЗ) здесь писать не надо, поскольку деления на переменную нет, и радикалов (корней) здесь не наблюдается.
На множители здесь все и так разложено за нас. Но не расслабляйся, это все, чтоб напомнить азы и понять суть!
Допустим, ты не знаешь метода интервалов, как бы ты стал решать это неравенство? Подойди логически и опирайся на то, что уже знаешь.
Во-первых, левая часть будет больше нуля если оба выражения в скобках либо больше нуля, либо меньше нуля, т.к. «плюс» на «плюс» дает «плюс» и «минус» на «минус» дает «плюс», так?
А если знаки у выражений в скобках разные, то в итоге левая часть будет меньше нуля.
А что же нам нужно, чтоб узнать те значения \( x\), при которых выражения в скобках будут отрицательными или положительными?
Нам нужно решить уравнение, оно точно такое же как неравенство, только вместо знака «\( >\)» будет знак «\(=\)«.
Корни этого уравнения и позволят определить те пограничные значения, при отступлении \( x\) от которых множители \( (x+1)\) и \( (
А теперь сами интервалы.
Что такое интервал?
Это некий промежуток числовой прямой, то есть все возможные числа, заключенные между двумя какими-то числами – концами интервала. Эти промежутки в голове представить не так просто, поэтому интервалы принято рисовать, сейчас научу.
Эти точки «выкалываются» что означает, что они не относятся к числу тех значений, при которых неравенство верно. В данном случае, они выкалываются, т.к. знак в неравенстве \( >\), а не \(\ge\), то есть строго больше, а не больше или равно.
Хочу сказать, что ноль отмечать не обязательно, он без кружочков тут, а так, для понимания и ориентации по оси.
Ладно, ось нарисовали, точки (точнее кружочки) поставили, дальше что, как мне это поможет в решении? – спросишь ты.
Возьми значение для икса из интервалов по порядку и подставь их в свое неравенство и смотри, какой знак будет в результате умножения.
Такая куча текста вышла, а наглядности мало, правда?
Взгляни еще раз на неравенство \( (x+1)\cdot (
Теперь все на ту же ось наносим еще и знаки, которые получатся в результате. Ломаной линией в моем примере обозначаем положительные и отрицательные участки оси.
Смотри на неравенство – на рисунок, опять на неравенство – и снова на рисунок, что-нибудь понятно?
Постарайся теперь сказать на каких промежутках икса, неравенство будет верно.
Ну, раз ты с этим разобрался, то дело за малым – записать ответ!
В ответ пишем те промежутки, при которых левая часть больше нуля, \( x\in (-\infty ;-1)\cup (2;+\infty )\), что читается, как икс принадлежит промежутку от минус бесконечности до минус одного и от двух до плюс бесконечности.
Теперь пример, в котором тебе придется не только интервал рисовать.
Пример 1
\( (<
Пришло время раскрыть тебе один секрет, который я обещал еще в начале этой темы!
Можно не подставлять значения из каждого интервала для определения знака, а определить знак в одном из интервалов, а в остальных просто чередовать знаки!
Таким образом, мы сэкономили немного времени на проставлении знаков – думаю, это выигранное время на ЕГЭ не помешает!
Пример №2
Теперь рассмотрим пример дробно-рационального неравенства – неравенство, обе части которого являются рациональными выражениями (см. «Рациональные уравнения»).
Что можешь сказать про это неравенство? А ты взгляни на него как на дробно-рациональное уравнение, что делаем в первую очередь?
Сразу видим, что корней нет, значит точно рациональное, но тут же дробь, да еще и с неизвестным в знаменателе!
Метод интервалов, решение неравенств
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение квадратного неравенства
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
 |
Квадратное неравенство можно решить двумя способами:
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.
Если неравенство со знаком