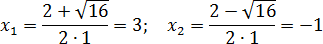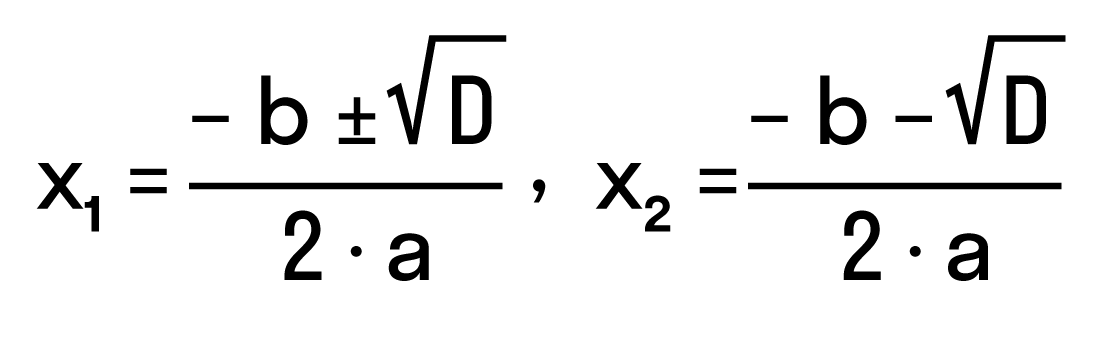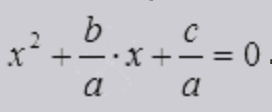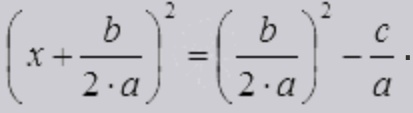Что значит решить квадратное уравнение
Решение квадратных уравнений
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.
Дискриминант
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
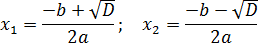
Первое уравнение:
x 2 − 2 x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2 x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
Наконец, третье уравнение:
x 2 + 12 x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид a x 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
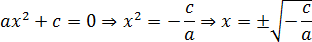
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (− c / a ) ≥ 0. Вывод:
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
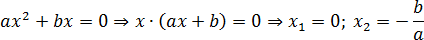
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
x 2 − 7 x = 0 ⇒ x · ( x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5 x 2 + 30 = 0 ⇒ 5 x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4 x 2 − 9 = 0 ⇒ 4 x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Как решать
квадратные уравнения
В предыдущих уроках мы разбирали «Как решать линейные уравнения», то есть уравнения первой степени. В этом уроке мы разберем, что называют квадратным уравнением и как его решать.
Что называют квадратным уравнением
Степень уравнения определяют по наибольшей степени, в которой стоит неизвестное.
Если максимальная степень, в которой стоит неизвестное — « 2 », значит, перед вами квадратное уравнение.
Примеры квадратных уравнений
Чтобы найти « a », « b » и « c » нужно сравнить свое уравнение с общим видом квадратного уравнения « ax 2 + bx + c = 0 ».
Давайте потренируемся определять коэффициенты « a », « b » и « c » в квадратных уравнениях.
Как решать квадратные уравнения
В отличии от линейных уравнений для решения квадратных уравнений используется специальная формула для нахождения корней.
Чтобы решить квадратное уравнение нужно:
Давайте на примере разберем, как применять формулу для нахождения корней квадратного уравнения. Решим квадратное уравнение.
Уравнение « x 2 − 3x − 4 = 0 » уже приведено к общему виду « ax 2 + bx + c = 0 » и не требует дополнительных упрощений. Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения.
Определим коэффициенты « a », « b » и « c » для этого уравнения.
Подставим их в формулу и найдем корни.
x 2 − 3x − 4 = 0
x1;2 =
| −b ± √ b 2 − 4ac |
| 2a |
x1;2 =
| −(−3) ± √ (−3) 2 − 4 · 1· (−4) |
| 2 · 1 |
x1;2 =
| 3 ± √ 9 + 16 |
| 2 |
x1;2 =
| 3 ± √ 25 |
| 2 |
x1;2 =
| 3 ± 5 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 4 | x2 = −1 |
Ответ: x1 = 4 ; x2 = −1
Обязательно выучите наизусть формулу для нахождения корней.
С её помощью решается любое квадратное уравнение.
Рассмотрим другой пример квадратного уравнения.
В данном виде определить коэффициенты « a », « b » и « c » довольно сложно. Давайте вначале приведем уравнение к общему виду « ax 2 + bx + c = 0 ».
Теперь можно использовать формулу для корней.
x1;2 =
| −(−6) ± √ (−6) 2 − 4 · 1 · 9 |
| 2 · 1 |
x1;2 =
| 6 ± √ 36 − 36 |
| 2 |
x1;2 =
| 6 ± √ 0 |
| 2 |
x1;2 =
| 6 ± 0 |
| 2 |
x =
| 6 |
| 2 |
x = 3
Ответ: x = 3
Бывают случаи, когда в квадратных уравнениях нет корней. Такая ситуация возникает, когда в формуле под корнем оказывается отрицательное число.
Рассмотрим пример квадратного уравнения, у которого нет корней.
5x 2 + 2x = − 3
5x 2 + 2x + 3 = 0
x1;2 =
| −2 ± √ 2 2 − 4 · 3 · 5 |
| 2 · 5 |
x1;2 =
| −2 ± √ 4 − 60 |
| 10 |
x1;2 =
| −2 ± √ −56 |
| 10 |
Ответ: нет действительных корней.
Итак, мы получили ситуацию, когда под корнем стоит отрицательное число. Это означает, что в уравнении нет корней. Поэтому в ответ мы так и записали «Нет действительных корней».
Что означают слова «нет действительных корней»? Почему нельзя просто написать «нет корней»?
На самом деле корни в таких случаях есть, но в рамках школьной программы они не проходятся, поэтому и в ответ мы записываем, что среди действительных чисел корней нет. Другими словами «Нет действительных корней».
Неполные квадратные уравнения
Иногда встречаются квадратные уравнения, в которых отсутсвуют в явном виде коэффициенты « b » и/или « c ». Как например, в таком уравнении:
Такие уравнения называют неполными квадратными уравнениями. Как их решать рассмотрено в уроке «Неполные квадратные уравнения».
Решение квадратных уравнений: формула корней, примеры
В продолжение темы «Решение уравнений» материал данной статьи познакомит вас с квадратными уравнениями.
Рассмотрим все подробно: суть и запись квадратного уравнения, зададим сопутствующие термины, разберем схему решения неполных и полных уравнений, познакомимся с формулой корней и дискриминантом, установим связи между корнями и коэффициентами, ну и конечно приведем наглядное решение практических примеров.
Квадратное уравнение, его виды
Зачастую квадратные уравнения также носят название уравнений второй степени, поскольку по сути квадратное уравнение есть алгебраическое уравнение второй степени.
Приведенные и неприведенные квадратные уравнения
По значению первого коэффициента квадратные уравнения подразделяют на приведенные и неприведенные.
Любое неприведенное квадратное уравнение возможно преобразовать в приведенное уравнение, если разделить обе его части на первый коэффициент (равносильное преобразование). Преобразованное уравнение будет иметь такие же корни, как и заданное неприведенное уравнение или так же не иметь корней вовсе.
Рассмотрение конкретного примера позволит нам наглядно продемонстрировать выполнение перехода от неприведенного квадратного уравнения к приведенному.
Задано уравнение 6 · x 2 + 18 · x − 7 = 0 . Необходимо преобразовать исходное уравнение в приведенную форму.
Решение
Полные и неполные квадратные уравнения
В случае же, когда коэффициенты b и c равны нулю (что возможно, как по отдельности, так и совместно), квадратное уравнение носит название неполного.
Полное квадратное уравнение – квадратное уравнение, в котором все числовые коэффициенты не равны нулю.
Порассуждаем, почему типам квадратных уравнений даны именно такие названия.
Решение неполных квадратных уравнений
Заданное выше определение дает возможность выделить следующие виды неполных квадратных уравнений:
Рассмотрим последовательно решение каждого вида неполного квадратного уравнения.
Решение уравнения a·x 2 =0
Кратко решение оформляется так:
Решение уравнения a · x 2 + c = 0
Резюмируем все рассуждения выше.
Решение
Ответ: уравнение 9 · x 2 + 7 = 0 не имеет корней.
Решение
Решение уравнения a·x 2 +b·x=0
Закрепим материал примером.
Решение
Кратко решение уравнения запишем так:
Дискриминант, формула корней квадратного уравнения
Для нахождения решения квадратных уравнений существует формула корней:
Нелишним будет понимать, как была выведена указанная формула и каким образом ее применять.
Вывод формулы корней квадратного уравнения
Вновь сформулируем выводы:
Так, результатом наших рассуждений стало выведение формулы корней квадратного уравнения:
Данные формулы дают возможность при дискриминанте больше нуля определить оба действительных корня. Когда дискриминант равен нулю, применение обеих формул даст один и тот же корень, как единственное решение квадратного уравнения. В случае, когда дискриминант отрицателен, попытавшись использовать формулу корня квадратного уравнения, мы столкнемся с необходимостью извлечь квадратный корень из отрицательного числа, что выведет нас за рамки действительных чисел. При отрицательном дискриминанте у квадратного уравнения не будет действительных корней, но возможна пара комплексно сопряженных корней, определяемых теми же полученными нами формулами корней.
Алгоритм решения квадратных уравнений по формулам корней
Решить квадратное уравнение возможно, сразу задействуя формулу корней, но в основном так поступают при необходимости найти комплексные корни.
В основной же массе случаев обычно подразумевается поиск не комплексных, а действительных корней квадратного уравнения. Тогда оптимально перед тем, как использовать формулы корней квадратного уравнения, сначала определить дискриминант и удостовериться, что он не является отрицательным (в ином случае сделаем вывод, что у уравнения нет действительных корней), а после приступить к вычислению значения корней.
Рассуждения выше дают возможность сформулировать алгоритм решения квадратного уравнения.
Примеры решения квадратных уравнений
Приведем решение примеров при различных значениях дискриминанта.
Решение
Решение
Необходимо решить уравнение 5 · y 2 + 6 · y + 2 = 0
Решение
В случае, когда стоит задача указать комплексные корни, применим формулу корней, выполняя действия с комплексными числами:
В школьной программе стандартно нет требования искать комплексные корни, поэтому, если в ходе решения дискриминант определен как отрицательный, сразу записывается ответ, что действительных корней нет.
Формула корней для четных вторых коэффициентов
Пусть выражение n 2 − a · c будет обозначено как D 1 (иногда его обозначают D ‘ ). Тогда формула корней рассматриваемого квадратного уравнения со вторым коэффициентом 2 · n примет вид:
Решение
Возможно было бы произвести вычисления и по обычной формуле корней квадратного уравнения, но в таком случае решение было бы более громоздким.
Упрощение вида квадратных уравнений
Иногда существует возможность оптимизировать вид исходного уравнения, что позволит упростить процесс вычисления корней.
Такое преобразование возможно, когда коэффициенты квадратного уравнения не являются взаимно простыми числами. Тогда обычно осуществляют деление обеих частей уравнения на наибольший общий делитель абсолютных величин его коэффициентов.
Связь между корнями и коэффициентами
Самыми известными и применимыми являются формулы теоремы Виета:
Также можно найти ряд прочих связей между корнями и коэффициентами квадратного уравнения. Например, сумма квадратов корней квадратного уравнения может быть выражена через коэффициенты:
Как решать квадратные уравнения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие квадратного уравнения
Уравнения — это математическое равенство, в котором неизвестна одна или несколько величин. Значения неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать выражение 3 + x = 7, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.
Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Есть три вида квадратных уравнений:
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент может быть любым.
Давайте-ка на примерах — вот у нас есть два уравнения:
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято назвать неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.
Решение неполных квадратных уравнений
Как мы уже знаем, есть три вида неполных квадратных уравнений:
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.
Как решить уравнение ax 2 = 0
Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.
Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.
Пример 1. Решить −6x 2 = 0.
Как решить уравнение ax 2 + с = 0
Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению ax 2 + c = 0, которое:
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.
Как решить уравнение ax 2 + bx = 0
Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:
Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:
Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0
0,5x = 0,125,
х = 0,125/0,5
Ответ: х = 0 и х = 0,25.
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:
Обратная теорема Виета
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0.
Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.
Пример 1. Решить при помощи теоремы Пифагора: x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″>
Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам:
Как разложить квадратное уравнение
С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:
Формула разложения квадратного трехчлена
Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2).
Дискриминант: формула корней квадратного уравнения
Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:
где D = b 2 − 4ac — дискриминант квадратного уравнения.
Эта запись означает:
Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.
Выводим формулу корней квадратного уравнения
Продолжим изучать формулу корней квадратного уравнения.
Пусть перед нами есть задача решить квадратное уравнение ax 2 + bx + c = 0. Выполним ряд равносильных преобразований:

после чего уравнение примет вид
Так, мы пришли к уравнению 
Отсюда выводы про корни уравнения 
И еще один вывод: есть у уравнения корень или нет, зависит от знака выражения в правой части. При этом важно помнить, что знак этого выражения задается знаком числителя. Потому выражение принято называть дискриминантом квадратного уравнения и обозначается буквой D.
По значению и знаку дискриминанта можно сделать вывод, есть ли действительные корни у квадратного уравнения, и сколько.
Алгоритм решения квадратных уравнений по формулам корней
Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!
Примеры решения квадратных уравнений
Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.
Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.
Ответ: единственный корень 3,5.
Пример 2. Решить уравнение 54 — 6x 2 = 0.
Ответ: два корня 3 и — 3.
Пример 3. Решить уравнение x 2 — х = 0.
Ответ: два корня 0 и 1.
Пример 4. Решить уравнение x 2 — 10 = 39.
Ответ: два корня 7 и −7.
Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.
D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112
В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.
Формула корней для четных вторых коэффициентов
Рассмотрим частный случай. Формула решения корней квадратного уравнения 
2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″>
Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.
Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
Упрощаем вид квадратных уравнений
Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.
Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0.
Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100.
Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.
А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения
умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.
Связь между корнями и коэффициентами
Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:
Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.
Например, можно применить формулы из теоремы Виета:
Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:
А еще найти корни квадратного уравнения можно с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников: