Что значит разложить вектор по координатным векторам
Координаты вектора в декартовой системе координат (ДСК)
Для начала дадим определение координат вектора в заданной системе координат. Чтобы ввести данное понятие, определим что мы называем прямоугольной или декартовой системой координат.
Прямоугольная система координат представляет из себя прямолинейную систему координат с взаимно перпендикулярными осями на плоскости или в пространстве.
С помощью введения прямоугольной системы координат на плоскости или в трехмерном пространстве становится возможным описывание геометрических фигур вместе с их свойствами при помощи уравнений и неравенств, то есть использовать алгебраические методы при решении геометрических задач.
Тем самым, мы можем привязать к заданной системе координат векторы. Это значительно расширит наши возможности при решении определенных задач
Координатные векторы
Векторы i → и j → называются координатными векторами для заданной системы координат.
Разложение вектора
Коэффициенты a x и a y называются координатами вектора в данной системе координат на плоскости.
Следует обратить внимание, что порядок записи координат, имеет важное значение, если вы запишите координаты вектора в другом порядке, вы получите совершенно другой вектор.
Равные и противоположные векторы
Векторы a → и b → равны тогда, когда их соответствующие координаты равны.
Противоположным вектором называется вектор противоположный данному.
Координаты радиус-вектора точки
Чтобы ввести данное определение, требуется показать в данной системе координат связь координат точки и координат вектора.
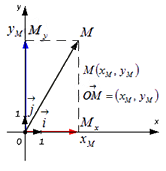
Вектор O M → называется радиус-вектором точки M .
Определим, какие координаты в данной системе координат имеет радиус-вектор точки
Иначе говоря, координаты радиус-вектора точки М равны соответствующим координатам точки М в прямоугольной декартовой системе координат.
Разложение вектора по двум неколлинеарным векторам. Координаты вектора.
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Разложение вектора по двум неколлинеарным векторам.
Напомним, что коллинеарными называются векторы, лежащие на одной прямой или на параллельных прямых. Соответственно, неколлинеарными будут векторы, которые не лежат на одной прямой и не параллельны.
Любой вектор можно разложить (т.е. представить в виде суммы или разности) по двум неколлинеарным векторам. Мы докажем такую теорему, но чуть позже. Сначала лемма.
По условию, векторы и коллинеарны, значит, они либо лежат на одной прямой, либо на параллельных прямых. Доказательство для обоих случаев одинаково, поэтому рассмотрим второй из них. Коллинеарные векторы могут быть сонаправленными или противоположно направленными.
Посмотрим, какое соотношение имеют длины этих векторов.
Посмотрим, какое соотношение имеют длины этих векторов.
ТЕОРЕМА. На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.
. В этом случае формула также доказана.
Перечислим и проверим некоторые свойства действий с координатами векторов.
Равные векторы имеют равные координаты.
На рисунке видно, что если векторы равны, то неважно в каком месте на координатной плоскости они располагаются. У них будет одинаковое разложение по координатным векторам, а значит, и равные координаты.
Каждая координата суммы (или разности) двух или более векторов равна сумме (или разности) соответствующих координат этих векторов.
Значит, вектор суммы (или разности) имеет координаты, равные сумме (или разности) соответствующих координат данных векторов, т.е. .
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Воспользуемся сначала правилом умножения вектора на число, а затем правилом сложения векторов.
При каком значении параметра векторы и коллинеарны?
Отрезок разделён на шесть равных частей. Найдите значение числового множителя в каждом равенстве:
Докажите, что если векторы и неколлинеарны, то векторы и тоже неколлинеарны.
Отложите данные векторы от указанных точек.
При каком значении параметра векторы и коллинеарны?
Будут ли векторы и коллинеарными?
Будут ли векторы и коллинеарными?
Разложите вектор по векторам:
Векторы и неколлинеарны. Найдите числа и такие, что:
На рисунке изображены векторы.
Напишите разложение вектора по координатным векторам.
Разложите по координатным векторам векторы:
Помогите Пожалуйста с вопросами по геометрии (9 класс)!
1)Сформулируйте и докажите лемму о коллинеарных векторах.
2)Что значит разложить вектор по двум данным векторам.
3)Сформулируйте и докажите теорему о разложении вектора по двум неколлинеарным векторам.
4)Объясните, как вводится прямоугольная системы координат.
5)Что такое координатные векторы?
6)Сформулируйте и докажите утверждение о разложении произвольного вектора по координатным векторам.
7)Что такое координаты вектора?
8)Сформулируйте и докажите правила нахождения координат суммы и разности векторов, а также произведения вектора на число по заданным координатам векторов.
9)Что такое радиус-вектора точки? Докажите, что координаты точки равны соответствующим координатам векторов.
10)Выведите формулы для вычисления координат вектора по координатам его начала и конца.
11)Выведите формулы для вычисления координат вектора по координатам его концов.
12) Выведите формулу для вычисления длины вектора по его координатам.
13)Выведите формулу для вычисления расстояния между двумя точками по их координатам.
14)Приведите пример решения геометрической задачи с применением метода координат.
15)Какое уравнение называется уравнением данной линии? Приведите пример.
16)Выведите уравнение окружности данного радиуса с центром в данной точке.
17)Напишите уравнение окружности данного радиуса с центром в начале координат.
18)Выведите уравнение данной прямой в прямоугольной системе координат.
19)Напишите уравнение прямых, проходящих через данную точку M0 (X0 : Y0) и параллельных осям координат.
20)Напишите уравнение осей координат.
21)Приведите примеры использования уравнений окружности и прямой при решении геометрических задач.
Пожалуйста очень надо!
В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.