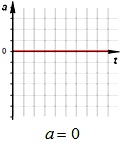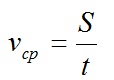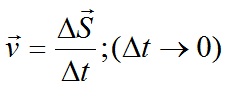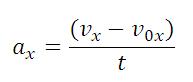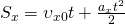Что значит равномерно и равноускоренно

Равномерное и равноускоренное движение

Вы будете перенаправлены на Автор24

Движение, при котором за одинаковые интервалы времени тело проходит неравное расстояние, называют неравномерным (или переменным).

При переменном движении скорость тела с течением времени меняется, по этой причине для характеристики подобного перемещения применяются определения средней и моментальной скоростей.

Из курса математики известно, что предел отношения приращения функции к приращению аргумента, когда последний стремится к 0 (если этот порог существует), выступает главной производной этой функции по данному аргументу.

Изучим, как скатывается шарик с наклонной плоскости. Шар перемещается неровно: пути, проходимые им за последовательные одинаковые интервалы периода, увеличиваются. Таким образом, темп передвижения шарика возрастает. Перемещение объекта, скатывающегося с косой плоскости, считается классическим примером прямолинейного равноускоренного перемещения.

Рассмотрим определение равноускоренного движения.

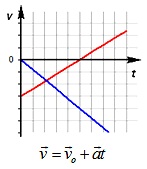
Прямолинейным равноускоренным движением именуют прямолинейное перемещение, при котором скорость тела за любые одинаковые интервалы времени меняется на одну и ту же величину.

Прямо равноускорено способен передвигаться, к примеру, транспорт в период разгона. Но необычным может представиться в таком случае, то что во время торможения машина также способна передвигаться прямолинейно равноускорено! Так как в определении равноускоренного перемещения речь никак не идет не о росте стремительности, а только лишь об изменении скорости.

Готовые работы на аналогичную тему

Суть в том, что представление ускорения в физике обширнее, нежели в обыденном понимании. В повседневной речи под ускорением подразумевают как правило только лишь повышение быстроты. Мы в физике станем говорить, то что тело перемещается с ускорением постоянно, если быстрота тела меняется любым способом (возрастает либо снижается согласно модулю, меняется согласно направленности и т.п.).

Может возникнуть вопрос: по какой причине мы уделяем внимание непосредственно прямолинейному равноускоренному перемещению? Забегая немножко вперед, скажем, что с этим перемещением мы будем часто иметь дело при рассмотрении законов механики.

Напомним, что под воздействием стабильной силы тело перемещается прямо равноускорено. (В случае если первоначальная скорость тела равна нулю либо ориентирована по линии воздействия силы.) А в многочисленных задачах из сферы механики рассматривается непосредственно такая ситуация, в которой применяются уравнения прямолинейного равноускоренного движения, формулы конечной скорости и формулы пути без времени.

Равноускоренное движение тела

Равноускоренное перемещение никак не обладает равной скоростью в течении всего пути прохождения. В этом случае имеется убыстрение, что отвечает за непрерывное повышение скорости. Ускорение перемещения остается постоянным, а темп регулярно и одинаково увеличивается.

Кроме равноускоренного имеется также равнозамедленное перемещение, где модуль темп одинаково уменьшается. Таким образом, равноускоренное перемещение способно проходить в некоторых измерениях. Оно бывает:

В случае первого — перемещение осуществляется по одной оси местоположение. В случае второго могут добавляться и прочие замеры.

Ускорение тела

Применять формулы перемещений при равноускоренном движении, а также формулы ускорения без времени возможно в абсолютно различных плоскостях. К примеру, с целью расчета падения жестких тел в свободном падении, места падения. В частности, для различных точных и геометрических расчетов.

Ускорение мы ассоциируем с увеличением скорости. Так как она ускоряется одинаково, получается равное увеличение скорости. Как понять, скорость равно увеличивается или нет? Нам нужно засечь время, оценить скорость через одинаковый промежуток времени, используя формулы ускорения при равноускоренном движении.

Например, автомобиль начал движение, за первые 2 сек он развил скорость до 10 м/с, за последующие 2 сек 20 м/с. Еще через 2 сек он уже едет со скоростью 30 м/с. Каждые 2 секунды темп возрастает и каждый раз на 10 м/с.

Такое передвижение и является равноускоренным. Ускорением называется величина, определяющая, насколько каждый раз увеличивается скорость. Кроме этого необходимо обратить внимание на формулу скорости при равноускоренном движении.

Равномерное движение

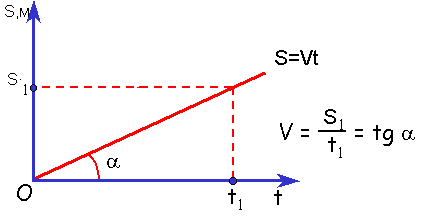
Механическое передвижение, при котором тело за всевозможные одинаковые интервалы времени проходит одну и ту же дистанцию является равномерным. При равномерном перемещении значение скорости точки остаётся стабильной (формула равномерного и равноускоренного движения).

Равномерное перемещение присутствует, если скорость предмета остается равной в каждом интервале пройденного пути, к этом случае период прохождения различных двух одинаковых участков будет одинаково.

В случае если перемещение является не только лишь равномерным, а и прямолинейным, в таком случае путь тела одинаковый с модулем передвижения. По этой причине, воспользовавшись аналогией с предшествующей формулой равноускоренного движения, в физике определяют скорость равномерного прямолинейного перемещения:

Скорость равномерного прямолинейного движения является вектором, так как перемещение – величина векторная. А значит, имеет не только числовое значение, но и пространственное направление.

Равноускоренное перемещение отлично от равномерного тем, что быстрота в этом перемещении регулярно и одинаково увеличивается, вплоть до конкретного предела. В равномерном же перемещении скорость не изменяется ни в коем случае, другим образом подобное перемещение никак не станет называться равномерным.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 08 08 2021

Источник

Равномерное и равноускоренное движение

В процессе такого перемещения скорость тела периодически изменяется, поэтому для описания данного процесса применяют понятия средней и мгновенной скоростей.

Мгновенная скорость – это скорость движения тела, которая фиксируется в конкретный момент времени в заданной точке пути. Другими словами, мгновенной скоростью \(v\) есть предел стремления средней скорости тела \(v_<ср>\) при бесконечно малом промежутке времени:

Известно, что предел отношения приращения функции к приращению аргумента, в случае стремления последнего к нулю, – это главная производная функции по аргументу.

Рассмотрим пример скатывания шарика по наклонной поверхности. При этом мы наблюдаем, что шарик движется неравномерно: расстояния, которые он проходит за одинаковые последовательные интервалы времени, постоянно увеличиваются. То есть, темп его движения постоянно растёт. Данное движение, как и скачивание любого предмета, является классикой прямолинейного равноускоренного перемещения.

Еще одним примером такого движения является перемещение транспорта, когда он разгоняется, а так же когда тормозит. То есть равноускоренным движением может считаться не только ускоренное, но и замедленное движение.

Дело в том, что понятие «ускорение» в физическом смысле более широкое, нежели мы привыкли использовать в ежедневной жизни. Слово ускорение в широком потреблении понимается как увеличение скорости, но физически под ускорением понимается передвижение тела с постоянным изменением скорости, при этом неважно увеличивается она или уменьшается.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Понятие прямолинейного равноускоренного движения достаточно широко используется при изучении законов механики.

Стоит отметить, что при влиянии постоянной силы тело будет перемещаться равноускорено.

Равномерное движение

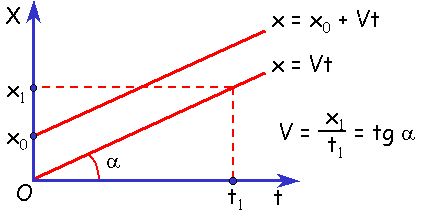
Равномерное движение – это такое механическое перемещение тела, когда за равные промежутки времени оно преодолевает равные расстояния.

Для равномерного перемещения характерно постоянное значение скорости:

где \(v\) – скорость равномерного перемещения, м/с;

\(l\) – расстояние, преодоленное объектом, м;

\(δt\) – промежуток времени перемещения, с.

При равномерном перемещении скорость предмета остаётся равной на каждом промежутке пути.

Если перемещение тела не только равномерное, а также прямолинейное, то его путь равен модулю его перемещения. Значит, аналогично предыдущему выражению, определяем скорость равномерного прямолинейного перемещения:

где \(\overline \) – скорость равномерного прямолинейного перемещения, м/с;

\(\overline\) – перемещение тела, м;

\(δt\) – промежуток времени перемещения, с.

Скорость равномерного прямолинейного перемещения является векторной величиной. То есть её направление также имеет значение, как и модуль.

Равноускоренное движение тела

При равноускоренном перемещении скорость постоянно изменяется. Если речь идет об убыстрении, скорость постоянно растет. То есть ускорение остаётся величиной постоянной, а темп постоянно растет.

Помимо равноускоренного движения еще выделяют равнозамедленное, где темп постоянно уменьшается с одинаковой быстротой.

Различают одномерное и многомерное ускорение. Первое происходит вдоль одной оси координат, а второе – в плоскости или в пространстве.

Не нашли что искали?

Просто напиши и мы поможем

Ускорение тела

Формулы равномерного движения для расчета ускорения могут применяться без учёта времени в разных плоскостях. Например, при расчёте свободного падения жестких тел, можно определять их местоположение. Это бывает полезно при различных геометрических расчётах.

Неравномерное перемещение тела, так же как и равноускоренное, характеризуется изменением скорости. Но в чём же тогда их отличие? При равноускоренном – скорость тела не просто изменяется, она равно ускоряется.

Понятие ускорения часто ассоциируют с ростом скорости. Поскольку скорость растет одинаково, говорят о равном возрастании скорости. Как же определить, скорость растет равномерно или нет? Для этого засекают время, оценивают приращение скорости за равные промежутки времени, если при этом приращение одинаково на каждом новом участке, передвижение считается равноускоренным.

Ускорение – это физическая величина, показывающая на сколько возрастает скорость.

Замедленным движением есть перемещение с уменьшающейся скоростью. Поскольку в физике любое перемещение с меняющейся скоростью называется ускоренным, то неважно разгоняется автомобиль либо тормозит, в любом случае он передвигается с ускорением.

Значит, ускорение описывает быстроту изменения скорости. Оно показывает на сколько меняется скорость за одну секунду. Чем больше величина ускорения, тем стремительнее тело набирает скорость либо сбрасывает её. Ускорение обозначается буквой a и определяется соотношением изменения скорости δv к промежутку времени δt, за которое оно осуществлено:

Источник

Как сказал.

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Я учу детей тому, как надо учиться

Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.

Урок 03. Лекция 03. Виды механического движения

Виды движения (равномерное, равноускоренное) и их графическое описание

По форме траектории движение делится на криволинейное (траектория движения тела кривая линия) и прямолинейное (траектория движения тела прямая линия).

При движении тела по прямолинейной траектории модуль вектора перемещения всегда совпадает с пройденным путём. При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути

Равномерное прямолинейное движение.

Прямолинейным равномерным движением называют движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

— это физическая векторная величина, равная отношению перемещения тела S за любой промежуток времен к значению этого промежутка t:

Уравнение равномерного движения ( перемещение тела при равномерном движении):

Уравнение координаты тела:

Обозначения:

х— координата движущегося тела

v _ср-Средняя скорость равномерного прямолинейного движения

v_х — Скорость равномерного прямолинейного движения

S — Перемещение тела (расстояние, на которое передвинулось тело)

t — Промежуток времени перемещения (время)

Графическое представление равномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

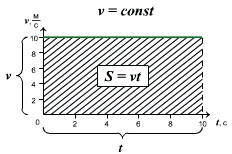
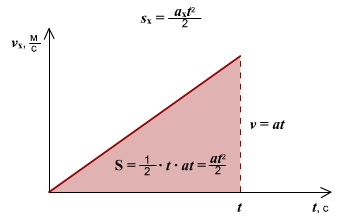
Проекция перемещения тела численно равна площади прямоугольника под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.

Из графика видно, что проекция скорости равна:

Рассмотрев эту формулу, мы можем сказать, чем больше угол a, тем быстрей движется тело и оно проходит больший путь за меньшее время.

Правило определения скорости по графику s(t) и x(t): Тангенс угла наклона графика к оси времени равен скорости движения.

Неравномерное прямолинейное движение.

Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.

Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным илипеременным движением.

Для характеристики неравномерного движения вводится понятие средней скорости.

Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.

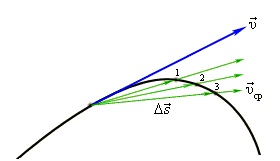
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:

Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.

Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.

Различие между средней и мгновенной скоростями показано на рисунке.

Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.

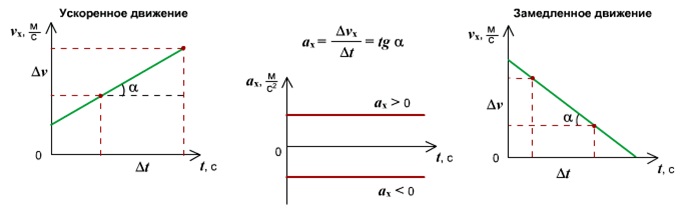
Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:

v_х — конечная скорость тела при равноускоренном движении по прямой

t — время движения тела

Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.

Единица измерения ускорения в СИ [ м/с 2 ].

Ускорение измеряют акселерометром

Уравнение скорости для равноускоренного движения:

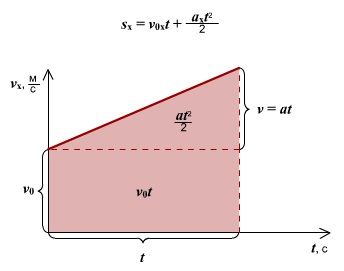
Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):

— Перемещение тела при равноускоренном движении по прямой

— Начальная скорость тела

— Скорость тела при равноускоренном движении по прямой

— Ускорение тела

— Время движения тела

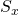
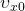
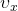
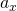
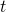
Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:

— если известны начальная, конечная скорости движения и ускорение.

— если известны начальная, конечная скорости движения и время всего движения

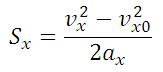
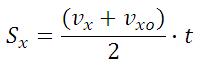
Графическое представление неравномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости .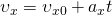

Графиком является наклонная линия.

Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратичной зависимости

В координатах зависимость имеет вид .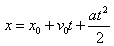

Источник

Кинематика

Механика — это раздел физики, изучающий механическое движение тел.

Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если

Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.

Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.

Основная задача механики — определить положение тела в пространстве в любой момент времени.

Механическое движение и его виды

Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.

Механическое движение может быть:
1. по характеру движения

2. по виду траектории

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​ \( S \) ​ — перемещение тела относительно неподвижной системы отсчета;
​ \( S_1 \) ​ — перемещение тела относительно подвижной системы отсчета;
​ \( S_2 \) ​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​ \( v \) ​ — скорость тела относительно неподвижной системы отсчета;
​ \( v_1 \) ​ — скорость тела относительно подвижной системы отсчета;
​ \( v_2 \) ​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.

Пусть \( v_1 \) — скорость первого тела, а \( v_2 \) — скорость второго тела.
Определим скорость первого тела относительно второго \( v_ <12>\) :

Определим скорость второго тела относительно первого \( v_ <21>\) :

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​ \( \alpha \) ​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Скорость

Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.

Обозначение — ​ \( v \) ​, единицы измерения — ​м/с (км/ч)​.

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.

Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

где ​ \( v \) ​ – конечная скорость; ​ \( v_0 \) ​ – начальная скорость;
​ \( t \) ​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​ \( a_n \) ​ – нормальное ускорение, ​ \( a_ <\tau>\) ​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если \( a_ <\tau>\) ≠ 0, \( a_n \) = 0, то тело движется по прямой;
если \( a_ <\tau>\) = 0, \( a_n \) = 0, ​ \( v \) ​ ≠ 0, то тело движется равномерно по прямой;
если \( a_ <\tau>\) = 0, \( a_n \) ≠ 0, тело движется равномерно по кривой;
если \( a_ <\tau>\) = 0, \( a_n \) = const, то тело движется равномерно по окружности;
если \( a_ <\tau>\) ≠ 0, \( a_n \) ≠ 0, то тело движется неравномерно по окружности.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

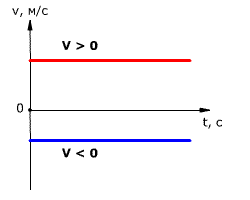
График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​ \( t \) ​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​ \( t \) ​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​ \( x=x(t) \) ​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение

Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.

Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):

При торможении (в проекциях на ось ОХ):

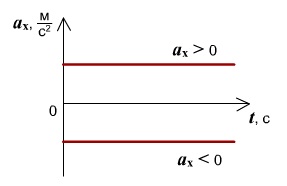
График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ​ \( a_x \) ​ > 0.
График 2 лежит под осью t, тело тормозит, \( a_x \) \( v_ <0x>\) ​ > 0, ​ \( a_x \) ​ > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, \( v_ <0x>\) > 0, \( a_x \) \( v_ <0x>\) \( a_x \) \( t_2-t_1 \) ​. Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ​ \( n \) ​-ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​ \( v_0 \) ​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​ \( v \) ​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​ \( v_0 \) ​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​ \( \alpha \) ​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​ \( T \) ​, единицы измерения – с.

где ​ \( N \) ​ – количество оборотов, ​ \( t \) ​ – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ​ \( \nu \) ​, единицы измерения – с –1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​ \( v \) ​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Мгновенная скорость нижней точки ​ \( (m) \) ​ равна нулю, мгновенная скорость в верхней точке ​ \( (n) \) ​ равна удвоенной скорости ​ \( v_1 \) ​, мгновенная скорость точки ​ \( (p) \) ​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​ \( (c) \) ​ – по теореме косинусов.

Источник