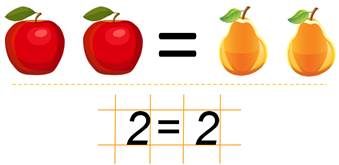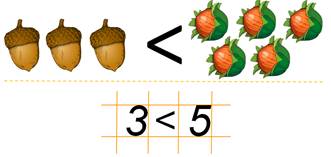Что значит равенство и неравенство

Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.

Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке:

Типы неравенств

Источник

Что такое числовые выражения, равенства, неравенства и уравнения

Выражение

Числовое выражение — это числа, соединённые знаками арифметических действий: сложение, вычитание, умножение и деление.

Найти значение числового выражения — это значит выполнить все указанные арифметические действия и получить конкретное число.

Кроме арифметических действий выражения могут содержать скобки, которые влияют на порядок действий при решении выражения.

Пример 1:

Равенство

Равенства — это числа или выражения, соединённые знаком = (равно).

Равенство считается верным, если числа или числовые выражения слева и справа от знака =, имеют равное значение.

Равенство считается неверным, если числа или числовые выражения слева и справа от знака =, не равны (≠).

При решении равенств соблюдается следующий порядок действий:

Пример 2:

1) 5 = 7 — равенство неверно, так как 5 ≠ 7.

2) 36 : 2 = 6 • 3 — равенство верно, так как:

3) 48 + 9 = 54 — 1 — равенство неверно, так как:

Неравенство

Пример 3:

1) 5 > 7 — неравенство неверно, так как 5

3) 4 + 5 • 6 > (4 + 5) • 6 — неравенство неверно, так как:

Уравнение

Уравнение — это равенство, которое содержит неизвестное число, обозначенное какой-либо латинской буквой: x, y, a, b, z, d и т.д.

Корень уравнения — это число, при подставлении котрого вместо буквы в равенство делает это равенство верным.

Решить уравнение — это значит найти все возможные корни уравнения.

Порядок и правила решения уравнений зависят от того, к какому типу они относятся:

Источник

Понятие равенства, знак равенства, связанные определения

Материал статьи позволит ознакомиться с математической трактовкой понятия равенства. Порассуждаем на тему сути равенства; рассмотрим его виды и способы его записи; запишем свойства равенства и проиллюстрируем теорию примерами.

Что такое равенство

Само понятие равенства тесно переплетено с понятием сравнения, когда мы сопоставляем свойства и признаки, чтобы выявить схожие черты. Процесс сравнения требует наличия двух объектов, которые и сравниваются между собой. Данные рассуждения наводят на мысль, что понятие равенства не может иметь место, когда нет хотя бы двух объектов, чтобы было что сравнивать. При этом, конечно, может быть взято большее количество объектов: три и более, однако, в конечном, счете, мы так или иначе придем к сравнению пар, собранных из заданных объектов.

Смысл понятия «равенство» в обобщенном толковании отлично определяется словом «одинаковые». О двух одинаковых объектах можно говорить – «равные». Например, квадраты и . А вот объекты, которые хоть по какому-то признаку отличаются друг от другу, назовем неравными.

Говоря о равенстве, мы можем иметь в виду как объекты в целом, так и их отдельные свойства или признаки. Объекты являются равными в целом, когда одинаковы по всем характеристикам. Например, когда мы привели в пример равенство квадратов, имели в виду их равенство по всем присущим им свойствам: форме, размеру, цвету. Также объекты могут и не быть равными в целом, но обладать одинаковыми отдельными признаками. Например: и . Указанные объекты равны по форме (оба – круги), но различны (неравны) по цвету и размеру.

Таким образом, необходимо заранее понимать, равенство какого рода мы имеем в виду.

Запись равенств, знак равно

Равенство – запись, в которой использован знак равно, разделяющий два математических объекта (или числа, или выражения и т.п.).

Верные и неверные равенства

Составленные равенства могут соответствовать сути понятия равенства, а могут и противоречить ему. По этому признаку все равенства классифицируют на верные равенства и неверные равенства. Приведем примеры.

Свойства равенств

Запишем три основных свойства равенств:

Буквенно сформулированные свойства запишем так:

Отметим особенную пользу второго и третьего свойств равенств – свойств симметричности и транзитивности – они дают возможность утверждать равенство трех и более объектов через их попарное равенство.

Двойные, тройные и т.д. равенства

При помощи таких цепочек равенств оптимально составлять равенство трех и более объектов. Такие записи по своему смыслу являются обозначением равенства любых двух объектов, составляющих исходную цепочку равенств.

Составляя подобные цепочки, удобно записывать последовательность решения примеров и задач: такое решение становится наглядным и отражает все промежуточные этапы вычислений.

Источник

Равенство и неравенство

Два числовых математических выражения, соединенные знаком «=» называют равенством.

Например: 3 + 7 = 10 — равенство.

Равенство может быть верным и неверным.

Смысл решения любого примера состоит в том, чтобы найти та­кое значение выражения, которое превращает его в верное равенство.

Для формирования представлений о верных и неверных равенствах в учебнике 1 класса используются примеры с окошком.

Методом подбора ребенок находит подходящие числа и проверяет верность равенства вычислением.

Процесс сравнения чисел и обозначение отношений между ними с помощью знаков сравнения приводит к получению неравенств.

Например: 5 4 — числовые неравенства

Неравенства также могут быть верными и неверными.

Методом подбора ребенок находит подходящие числа и проверяет верность неравенства.

Числовые неравенства получаются при сравнении числовых выражений и числа.

При выборе знака сравнения ребенок вычисляет значение выражения и сравнивает его с заданным числом, что отражается в выборе соответствующего знака:

10-2>7 5+К7 7 + 3>9 6-3 = 3

Возможен другой способ выбора знака сравнения — без ссылки на вычисления значения выражения.

Для постановки знаков сравнения можно провести такие рассуждения:

Сумма чисел 7 и 2 будет заведомо больше, чем число 7, значит, 7 + 2 > 7.

Для формирования представлений о верных и неверных равенствах и неравенствах в новой редакции учебника (2001) используются задания вида:

Для проверки используется метод вычисления значения выражений и сравнения полученных чисел.

Неравенства с переменной практически не используются в последних редакциях стабильного учебника математики, хотя в более ранних изданиях они присутствовали. Неравенства с переменными активно используются в альтернативных учебниках математики. Это неравенства вида:

После введения буквы для обозначения неизвестного числа такие неравенства приобретают привычный вид неравенства с переменной:

Источник

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Знаки: «>» больше, «

Однажды решили Белочка и Ёжик проверить, что птицы любят есть больше всего: пшеничные зерна или крошки белого хлеба. На один пень насыпали зерна, а на другой крошки хлеба и стали наблюдать.

— Ежик, ну что ты там видишь?

— О, теперь вижу. Два воробья прилетели. Сейчас зерна будут клевать.

— Ой. Ко второму пню, ну там где крошки, сорока наша прилетела.

— Так где птиц больше?

— На пне с зернышками птиц больше, чем около пня с крошками.

— Белочка, кажется дядя Филя прилетел.

— Ну, и где сейчас птиц стало больше?

— Теперь птиц стало одинаково.

— Любик, а ты знаешь, что в математике, чтобы сравнивать объекты или предметы используют специальные математические знаки: больше, меньше и равно.

Например, вот у нас одно яблоко и одна груша, т.е. яблок столько же сколько и груш. Значит между ними можно поставить знак равно. А записать это можно так: два равно двум.

Теперь мы сравним грибы: три боровика и две лисички. Что больше?

— Три боровика больше, чем две лисички.

— Правильно. В этом случае мы между грибами поставим знак больше. А записать это можно так: три больше чем два.

— А сейчас сравним жёлуди и орехи. Чего меньше?

— Ага… Желудей у нас три, а орехов пять. Значит желудей меньше, чем орехов.

— Правильно, в этом случае мы поставим знак меньше. А записать это можно так: пять меньше чем три.

А теперь мы посмотрим, как пишутся эти знаки.

— Я помню как пишется знак равно. Он состоит из двух палочек, которые пишутся друг под другом. Вот.

— Правильно. Знаки больше и меньше тоже состоят из двух палочек. В знаке больше палочки расходятся к большему числу, а записывается этот знак так.

В знаке меньше палочки сходятся к меньшему числу и записывается он так.

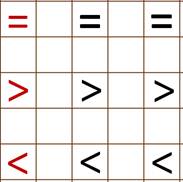
— Ежик, допиши пожалуйста знаки в строчку, в пустые клеточки.

— Ага… Сейчас, сейчас. Сначала допишу знак равно, теперь больше и меньше.

А чтобы ты не запутался, запомни: левая рука, согнутая в локте даст нам знак меньше, а правая рука согнутая в локте даст нам знак больше.

Если между двумя числами поставить знак равно, то получится числовое равенство. А если между двумя числами поставить знаки больше или меньше, то получится числовые неравенства.

Ежик, а теперь проверь пожалуйста, верные ли равенства и неравенства.

Так, так, так. Ага. Два больше чем один – все верно, три больше, чем четыре…ага…

что-то не так, три обозначает большее количество предметов, чем четыре и при счете

идет раньше, чем четыре значит это неравенство не верное. Мы его зачеркнем.

— А давай лучше исправим, чтобы у нас не было ошибок.

— Давай. Значит здесь надо поставить знак меньше. Вот.

— Так-так. Пять равно пяти. Все верно.

— Ага, а здесь совсем сложно.

— Ничего сложного. Смотри, чтобы проверить, надо сначала посчитать, сколько будет два да один.

— А сколько будет два да три.

— Пять. Значит три меньше пяти. Здесь опять ошибка. Надо поставить знак меньше.

— Ну молодец Ежик. Ты все правильно выполнил. Итак, ты должен запомнить:

1. Чтобы сравнить числа в математике используют знаки больше, меньше или равно.

2. Знак больше, расходится палочками к большему числу. И если согнуть правую руку в локте, то получится знак больше. Выражение, в котором стоит знак больше называется неравенство.

3. Знак меньше, сходится палочками к меньшему числу. И если согнуть левую руку в локте, то получится знак меньше. Выражение, в котором стоит знак меньше тоже называется неравенство.

4. Знак равно состоит из двух палочек, которые пишутся друг под другом, а выражение, в котором стоит знак равно называется числовым равенством.

— Белочка, а давай посмотрим, что там наши птицы делают?

— Все склевали и улетели. Да, теперь мы не сможем определить, что же птицы любят больше. Ничего не осталось.

— Наверное, Ежик, одни птицы больше любят есть зерна, а другие хлебные крошки.

Источник