Что значит простые числа в математике
Простые и составные числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Натуральные числа больше единицы бывают простые и составные.
Простое число — это натуральное число больше 1, у которого есть всего два делителя: единица и само число.
Составное число — похоже на простое. Это точно такое же натуральное число больше единицы, которое делится на единицу, на само себя и еще хотя бы на одно натуральное число.
Число 1 — не является ни простым, ни составным числом, так как у него только один делитель — 1. Именно этим оно отличается от всех остальных натуральных чисел.
Число 2 — первое наименьшее простое, единственное четное, простое число. Все остальные — нечетные.
Число 4 — первое наименьшее составное число.
В математике есть первые простые и составные числа, но последних таких чисел не существует.
А еще не существует простых чисел, которые оканчиваются на 4, 6, 8 или 0. В числе простых есть только одно число, которое заканчивается на 2 — и это само число 2. Из оканчивающихся на 5 — число 5. Все остальные оканчиваются на 1, 3, 7 или 9, за исключением 21, 27, 33 и 39.
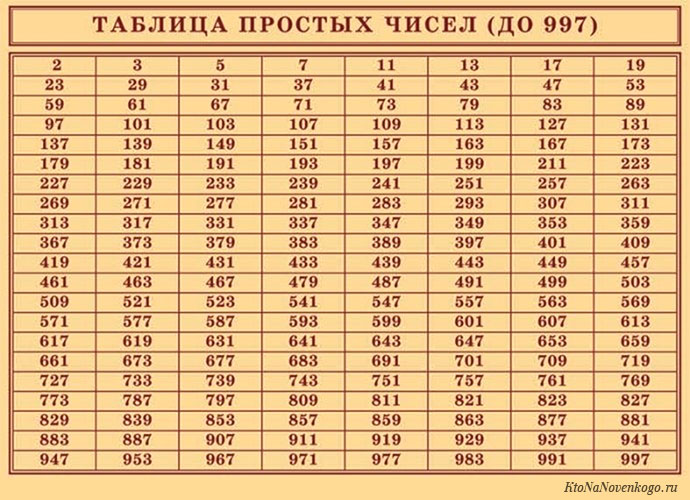
Таблица простых чисел до 1000
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 |
| 67 | 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 |
| 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 |
| 199 | 211 | 223 | 227 | 229 | 233 | 239 | 241 | 251 |
| 257 | 263 | 269 | 271 | 277 | 281 | 283 | 293 | 307 |
| 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 | 419 |
| 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 |
| 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 |
| 647 | 653 | 659 | 661 | 673 | 677 | 683 | 691 | 701 |
| 709 | 719 | 727 | 733 | 739 | 743 | 751 | 757 | 761 |
| 769 | 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 |
| 887 | 907 | 911 | 919 | 929 | 937 | 941 | 947 | 953 |
| 967 | 971 | 977 | 983 | 991 | 997 |
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Простые и составные числа, определения, примеры, таблица простых чисел, решето Эратосфена
В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.
Простые и составные числа – определения и примеры
Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.
Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.
Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.
Простые числа – это натуральные числа, имеющие только два положительных делителя.
Составное число – это натуральное число, имеющее более двух положительных делителей.
Натуральные числа, которые не являются простыми, называют составными.
Таблица простых чисел
Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:
Рассмотрим теорему, которая объясняет последнее утверждение.
Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.
Простых чисел бесконечно много.
Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.
Решето Эратосфена
Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.
Перейдем к формулировке теоремы.
Данное число простое или составное?
Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.
Доказать что число 898989898989898989 является составным.
Ответ: 11723 является составным числом.
Простые числа — это чудеса деления
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком математическом понятии, как ПРОСТЫЕ ЧИСЛА.
В школе это проходят в 5 или 6 классе, в зависимости от программы обучения.
И интересно, что если спросить школьников, что такое простые числа, то они, скорее всего, ответят правильно.
А вот взрослые задумаются и не факт, что вспомнят точное определение. Так что это статья скорее для них.
Простые числа — это.
Итак, вот как выглядит официальное определение:
Простые числа – это такие числа, которые имеют только два делителя. Один из них – единица, а другое – само число.
Чтобы было более понятно, приведем простой пример. Для чисел 5 и 7 надо найти все возможные делители, чтобы в результате образовалось целое число.
Если вы попробуете решить эту задачку, то получите, что 5 и 7 делятся только на 1 и 5, и 1 и 7 соответственно. Во всех других случаях вы получите дробное число. И это как раз означает, что числа 5 и 7 относятся к простым.
А вот попробуем по той же схеме разобрать числа 6 и 9. В первом случае мы получим, что 6 можно поделить на 1, 2, 3 и 6, а число 9 – на 1, 3 и 9. И это уже противоречит определению простых чисел, значит, 6 и 9 таковыми не являются.
Они называются в математике – СОСТАВНЫМИ ЧИСЛАМИ.
Список и таблица простых чисел
Некоторые ошибочно полагают, что наименьшее простое число – это единица.
С одной стороны, в этом есть логика, так как 1 делится только на 1. Но это получается одно и то же число (единица), что противоречит определению простых чисел, в котором четко прописано – «делителей должно быть два».
Значит, минимальное простое число – это 2. А первоначальный ряд выглядит следующим образом:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199…
При желании можете проверить эти числа на предмет деления. Мы же скажем, что этот ряд на самом деле не окончательный.
Количество простых чисел не ограничено. Или говоря математическим языком, оно стремится к бесконечности.
История простых чисел
Первые упоминания о простых числах относятся к Древнему Египту. В Британском музее хранится папирус, который датируется 2000 годом до нашей эры. И на нем, согласно расшифровке, содержится учебное пособие по арифметике.
В том числе и про деление чисел. Называется этот артефакт – папирус Райнда, по имени его первого владельца.
В этом документе есть таблица, в которой указаны числа, делящиеся на различные знаменатели. Причем они разделены таким образом, что становится понятно – древние египтяне может и не пользовались понятиям «простое число», но хотя бы имели о нем представление.
Ну а первые исследования простых чисел датируются 300 годом до нашей эры. И связаны они с именем знаменитого древнегреческого математика Евклида.
Как и многое другое, он описал простые и составные числа в своем известном произведении «Начала».
В частности, Евклид описал такие вещи, как:
Сейчас расскажем об этих понятиях подробнее.
Основная теорема арифметики
Основная теорема арифметики, которую придумал еще Евклид, гласит:
Любое натуральное число (это что?), которое больше единицы, может быть представлено в виде произведения простых чисел. Причем их количество не ограничено, а порядок следования неважен.
Если обозначить исходное число буквой N, а простые числа буквами Р1, Р2, Р3 и так далее, то можно записать эту теорему следующим образом:
N = Р1 * Р2 * Р3 * … * РК
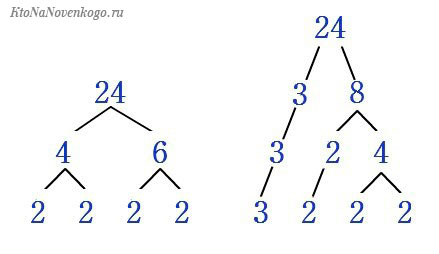
Например, возьмем число 100. Его можно разложить на следующие простые числа:
Или более сложный пример – число 23244:
23244 = 149 * 13 * 3 * 2 * 2
Раскладывать на простые числа легко. Можно сперва делить на 2 и 3, а уже в конце автоматически получить более сложные делители.
Ради интереса придумайте любое число и сами найдите его составляющие.
Лемма Евклида
Еще одна теорема, которая имеет прямое отношение к простым числам. Она гласит;
Если некое простое число Р делит произведение чисел X и Y без остатка, то оно может точно так же поделить или X, или Y.
Звучит несколько сложновато, хотя на деле все это просто. Так, возьмем для примера P = 2, X = 6, Y = 9. И тогда получается, что
В нашем примере P делит это произведение без остатка:
А значит наша P может поделить без остатка или X, или Y. Очевидно, что это X:
Y/P = 9/2 = 4,5 (не подходит)
Как быстро и легко определить простые числа
И еще одно понятие, которое связано с простыми числами. Оно названо в честь другого древнегреческого математика Эратосфена Киренского.
Этот человек придумал, как быстро и легко определить простые числа. В частности, он сделал таблицу, в которой были указаны значения до 1000.
Свою таблицу он нарисовал на глиняной дощечке. А после прокалывал те клеточки, на которых были написаны составные числа. В результате получилось нечто вроде решета, отсюда собственно и название метода.
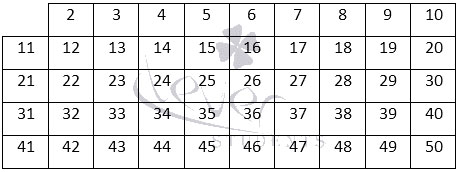
Кстати, пользоваться решетом Эратосфена весьма просто. Например, сделаем таблицу до 50.
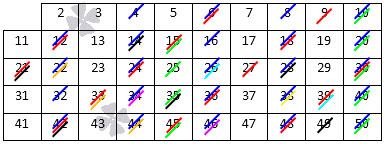
После этого из нее надо поочередно вычеркивать числа, которые кратны 2, 3, 5, 7 и 11. В результате получится вот это:
Те числа, которые остались, и есть простые. Можете сравнить этот ряд с тем, который мы давали в начале статьи. Точно таким же способом можно составить абсолютно любой ряд простых чисел = хоть до тысячи, хоть до миллиона и больше.
Вот и все, что мы хотели рассказать о ПРОСТЫХ ЧИСЛАХ в математике.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Математика весьма хитрая наука, да и простые числа не такие уж и простые, понимание простых и составных чисел привело человечество к тому техническому прогрессу, что окружает нас сейчас.
Простые числа
Простые числа намного полезнее, чем вы можете подумать, полагая их чисто умозрительными конструктами.
Простые числа — те числа, которые делятся без остатка только на само себя и 1. Это означает, что простое число нельзя представить в виде произведения (состоящего только из целых положительных чисел), кроме как:
[простое число] х 1 = [простое число]
Простые и составные
Составные числа — это числа, у которых есть делители, кроме самих себя и 1. Таким образом, все целые положительные числа, кроме 0 и 1, — либо простые, либо составные. Любое составное число можно представить в виде произведения простых сомножителей, то есть его можно разложить на множители, включающие только простые числа. Это наводит на мысль о важности простых чисел: это первичные блоки, из которых можно построить все остальные числа. Распределение простых чисел Теорема о распределении простых чисел, доказанная в XIX в., утверждает, что вероятность того, что случайным образом выбранное число n — простое, везде пропорциональна количеству цифр в нем, или логарифму n. Это означает, что чем больше число, тем меньше вероятность того, что оно будет простым.
Средний интервал между следующими друг за другом простыми числами к n приблизительно равен логарифму n, или ln(n).
Найти простое
Один из способов определения простого числа — «тест простоты». Если n — исследуемое число, то нужно попробовать разделить его на все числа больше 1 и меньше 1/2 n.
Самое большое обнаруженное простое число (на апрель 2015) содержит 17 425 170 знаков, это 2 57 885 161 – 1. Не стоит засиживаться до ночи, пытаясь выяснить следующее, если только вы не специализируетесь на этом, однако Фонд электронных рубежей (Electronic Frontier Foundation) назначил премию за первое простое число минимум в 100 миллионов знаков, а также за первое простое число минимум в пол миллиарда знаков.
Величайшие математические умы, а теперь еще и самые сложные компьютерные программы, давно пытаются найти закономерности в простых числах, но никакой предсказуемой закономерности до сих пор не было обнаружено.
Решето Эратосфена
Древнегреческий математик Евклид Александрийский, живший во II или III вв. до н. э., известен нам как первый человек, который выделил простые числа. Другой древнегреческий математик Эратосфен, II в. до н. э., представил свое так называемое «решето» для установления простых чисел. Оно годится только для относительно малых чисел, но его просто использовать.
Нарисуйте таблицу с 10 колонками и столькими рядами, сколько вам нужно, чтобы вместить числа, которые вы хотите проверить: если вы хотите проверить числа до n, нужно сделать таблицу от 1 до n. Начиная с 4, продвигайтесь по таблице и вычеркивайте все, что делится на 2. Затем вычеркните все, что делится на 3, затем — на 5, затем — на 7 и т. д., прокладывая путь сквозь простые числа. Когда вы доберетесь до делителя 1/2 n – 1, можете остановиться, так как большие числа не могут быть делителем n или меньших чисел. Числа, которые не были зачеркнуты, — простые.
Прискорбное пренебрежение
После Древней Греции и вплоть до XVII в. в интерес к простым числам почти отсутствовал. Даже в XVII в., простые числа не использовались нигде, кроме как в чистой математике, но ими, по крайней мере, стало позволительно поиграть. Они заняли свое законное место в компьютерную эпоху, с появлением необходимости в разработке шифровальных алгоритмов.
Есть работа
Простые числа пребывали в ленивом бездействии, пока не пришла необходимость в шифровании данных. Сейчас мы ежедневно посылаем несметное количество защищенных транзакций и других секретных данных через интернет, а простые числа предоставляют аналог защищенных фургонов, в которых перевозят данные. Начнем, перемножив два очень больших простых числа, чтобы получить составное число:
Составное число используется для генерации кода, который называется открытый ключ, который банк (или кто-нибудь) посылает человеку, желающему зашифровать свои данные. Если вы покупаете что-нибудь онлайн, данные вашей кредитки должны быть зашифрованы с использованием этого публичного ключа, шифрование происходит на вашем конце связи. Зашифрованные данные окажутся пустым набор слов, если будут перехвачены в процессе передачи. Когда данные вашей карты прибывают на другой конец, закрытый ключ — созданный из Р1 и Р2 — используется для расшифровки.
Это работает, так как очень сложно найти простые числа, из которых было получено составное, когда речь идет о больших числах. Любому хакеру понадобится 1000 лет компьютерного времени, чтобы взломать код и найти первоначальные простые числа. Именно потому, что так сложно взломать современный шифр, правительства скорее действительно предпочтут, чтобы разработчики встраивали «бэкдор» в свои системы, что позволяет им порой следить за тем, что делают люди.