Что значит пространство во времени
Спросите Итана: существуют ли разные типы пространства и времени?
Одно из самых неинтуитивных следствий теории относительности Эйнштейна состоит в том, что не существует абсолютного пространства или абсолютного времени. Если спросить вас, где и когда вы находитесь, вы ответите. Но если мы с вами разойдёмся на большое расстояние, и я спрошу вас, где и когда, как вам кажется, нахожусь я, то наши с вами ответы не обязательно совпадут. Оказывается, в общей теории относительности не существует универсального метода определения пространства и времени (и расстояний) кроме того места, где находитесь вы. В результате у нас есть множество способов определять такие вещи, и именно с этим связан вопрос читателя:
Я хотел бы увидеть ваше объяснение конформного времени и сопутствующего расстояния – что это такое, когда и как их используют по сравнению с привычными временем и расстоянием.
Используя в обычной речи такие понятия, как «время» и «расстояние», мы делаем множество предположений, о которых очень редко задумываемся.
Если вы считаете, что вы можете сообщить мне, что там, где нахожусь я, время дня равняется 10:05 утра, а нахожусь я от вас на расстоянии в 700 метров, вы можете не понимать, на каком основании вы уверены в своих оценках. Вы предполагаете, что наши с вами часы идут с одинаковой скоростью, что они происходят из одного места, в котором мы с вами согласовали значение времени, и что когда мы вновь сведём эти часы вместе, они также будут согласовываться друг с другом. Всё просто, не правда ли?
Но это возможно, только если выполняются два важных условия:
1. Ничего не двигается по отношению ко всему остальному. Если два объекта приобретают скорость друг относительно друга, они испытывают течение времени (и ощущение расстояния) по-разному. Нестабильные частицы, движущиеся со скоростями, близкими к скорости света, кажутся нам живущими дольше из-за растяжения времени, а космонавты на борту МКС, быстро двигающиеся вокруг Земли, стареют немного не так, как люди, находящиеся неподвижно на Земле.
2. Пространство абсолютно плоское, чего никогда не бывает. Во Вселенной работает ОТО, а согласно ей существование материи и энергии означает, что пространство искривлено, и что часы идут с разными скоростями в зависимости от глубины погружения в гравитационное поле. Часы на верхушке Эмпайр-стейт-билдинг каждый год отстают на несколько микросекунд от часов у её подножия.
Те же ограничения действуют и для расстояний: движение и кривизна пространства делают невозможным для наблюдателей в разных местах принять универсальный стандарт расстояний. Но для действительно больших расстояний начинает играть роль ещё кое-что: факт расширения самой ткани пространства Вселенной на космических масштабах. Мы уже не можем говорить о расстояниях между галактиками как о том, что можно измерить некоей согласованной линейкой, поскольку пространство между галактиками со временем расширяется. И это приводит к проблемам, когда мы начинаем говорить, к примеру, о самых отдалённых галактиках во Вселенной.
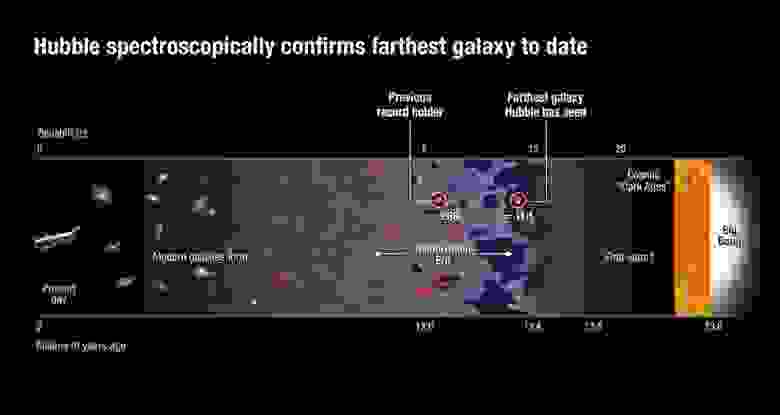
Текущий космический рекордсмен по расстояниям расположен на красном смещении в 11,1 что означает, что за время существования Вселенной, 13,8 млрд лет с Большого взрыва, его свет дошёл до нас, побыв в пути 13,4 млрд лет. Но как далеко от нас эта галактика? Вы могли бы на основе времени, затраченного на путь, решить, что она находится на расстоянии в 13,4 млрд световых лет – но это вряд ли так. Когда свет, дошедший до нас, был испущен этой галактикой, она находилась не более, чем в двух млрд световых лет от нас. Благодаря расширению Вселенной мы, используя общепринятый стандарт измерений, можем сказать, что сейчас она находится в 32 млрд световых лет от нас. Универсальный стандарт расстояний тяжело определить в расширяющейся Вселенной, в которой расстояния меняются со временем.
Так что одно из вводимых нами понятий при ответе на вопрос читателя – концепция разных типов расстояний. Он спрашивает нас об одном из них – о сопутствующем расстоянии. Это одно из моих любимых понятий: оно подразумевает, что расстояния во Вселенной изменяются из-за Хаббловского расширения, поэтому оно исключает расширение из вычислений. Это очень удобно для проведения симуляций формирования таких структур Вселенной, как звёзды, галактики, скопления и нити. Гравитация, конечно, вносит свою лепту, но и Вселенная всё это время расширяется. Зная, как сделать поправку расстояний на расширение, мы можем увидеть, как эволюционируют крупномасштабные структуры Вселенной. Визуально за этим наблюдать гораздо интереснее, чем следить за расширением Вселенной и пытаться различить во всём этом процесс формирования структур.
Поскольку пространство и время неразрывно связаны в объединяющую их концепцию пространства-времени, нам необходимо новое понятие о времени, соответствующее каждому из новых понятий расстояний, которые мы изобретём. Временным партнёром сопутствующего расстояния и будет конформное время. Если бы мы могли волшебным образом мгновенно заморозить всё расширение Вселенной во всех местах, то конформное время соответствует тому, сколько световому лучу потребуется времени на путь из некоего места до вас.
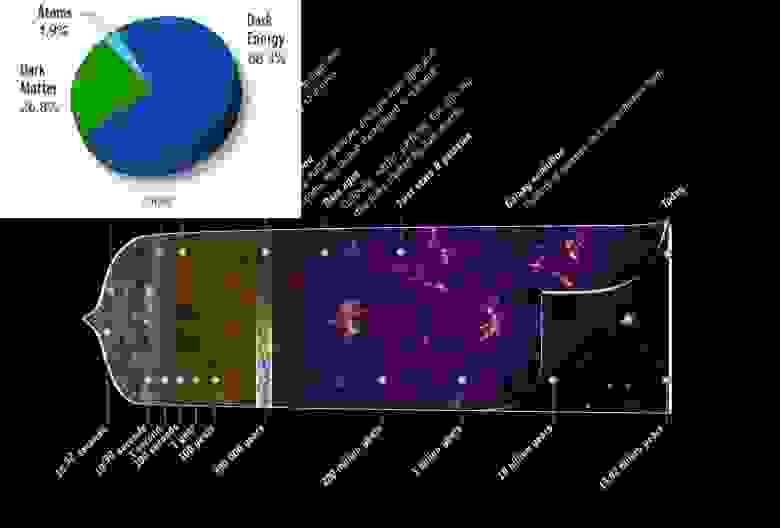
Для наиболее удалённой от нас галактики во Вселенной конформное время составит 32 млрд лет. Для воспринимаемого расстояния от Большого взрыва оно составит 46 млрд лет. И это несмотря на то, что от Большого взрыва до испускания света первой галактикой прошло 400 млн лет. На ранних этапах расширение Вселенной было таким быстрым – и результат этого ощущается и сегодня – что разница в 14 млрд лет конформного времени соответствует разнице в 400 млн лет «правильного» времени (того, которое мы называем просто «время»).
Если рассуждать о событиях, происходящих на Земле, где ничего не движется со скоростями, близкими к световой и не меняется слишком сильно в гравитационном поле, то различные типы «расстояний» и «времён» будут совпадать. Но если говорить о расширяющейся Вселенной на космических масштабах, то правильное расстояние и правильное время могут быть не такими полезными и интересными, как сопутствующее расстояние и конформное время. И в следующий раз, когда вы увидите симуляцию Вселенной и увидите, что Вселенная не выглядит расширяющейся, имейте в виду, что симуляция проходит с использованием сопутствующих расстояний, хотя и может использовать правильное время.
А когда вы услышите что-нибудь об очень удалённом объекте, находящемся от нас на расстоянии меньшем, чем 14 млрд световых лет, имейте в виду, что, скорее всего, речь идёт о сопутствующем расстоянии. Согласно нашим обычным, правильным линейкам, это расстояние, скорее всего, будет гораздо большим!
Спросите Итана: пространство-время – реальная сущность или просто концепция?

Схема сильного искривления пространства-времени вблизи горизонта событий чёрной дыры. Чем ближе вы приближаетесь к массивному телу, тем сильнее искривляется пространство. В итоге вы оказываетесь в таком месте, откуда не может убежать даже свет: внутри горизонта событий.
Большинство людей, думая о Вселенной, представляют себе материальные объекты, находящиеся на огромных космических расстояниях друг от друга. Под действием собственной гравитации материя схлопывается, формируя такие космические структуры, как галактики. Газовые облака, сжимаясь, порождают звёзды и планеты. Звёзды испускают свет, сжигая топливо в реакциях ядерного синтеза. Этот свет проходит по всей Вселенной, подсвечивая всё, на что натолкнётся. Однако Вселенная – это не только объекты внутри неё. Есть ещё и ткань пространства-времени, играющая по своим правилам – по правилам общей теории относительности (ОТО). Ткань пространства-времени искривляется в присутствии материи и энергии, при этом само искривление ткани пространства-времени диктует материи и энергии, как им двигаться. Но что такое, конкретно, пространство-время – это нечто «реальное», или просто облегчающий подсчёты инструмент? Об этом нас спрашивает читатель:
Что именно представляет собой пространство-время? Это реальная штука типа атомов, или математический конструкт, используемый для описания того, как масса «порождает» гравитацию?
Отличный вопрос, а его тема достаточно сложна для размышлений. Более того, до появления Эйнштейна наше представление о Вселенной сильно отличалось от текущего. Давайте вернёмся в далёкое прошлое Вселенной, когда у нас ещё не было концепции пространства-времени, и будем двигаться вперёд, до сегодняшнего дня.

На всех масштабах, от макроскопических до субатомных, размеры фундаментальных частиц играют мало роли в определении конечных размеров составных структур. Являются ли эти строительные кирпичики материи воистину фундаментальными точечными частицами, неизвестно до сих пор. Однако мы разбираемся в строении Вселенной от гигантских, космических масштабов, до крохотных, субатомных. К примеру, в человеческом теле содержится около 10 28 атомов.
На фундаментальном уровне мы уже давно подозревали, что если взять какой угодно объект во Вселенной, и начать делить его на всё меньшие и меньшие составные части, в итоге можно достичь чего-то неделимого. Слово «атом» буквально и означает «неделимый», от греческого ἄτομος. Первое упоминание об этой идее встречается 2400 лет назад, у Демокрита. Однако вполне вероятно, что идею могли придумать и раньше. Такие неделимые сущности реально существуют – они известны, как квантовые частицы. Несмотря на то, что мы назвали атомами элементы таблицы Менделеева, истинно неделимыми являются субатомные частицы – кварки, глюоны и электроны (а также те частицы, что вовсе не встречаются в атомах).
Все эти кванты связываются вместе и составляют все известные нам сегодня составные структуры Вселенной – от протонов и атомов до молекул и людей. И все эти кванты, вне зависимости от их типа – материя это или антиматерия, есть у них масса или нет, фундаментальные они или составные, субатомные у них масштабы или космические – существуют в рамках той же самой Вселенной, что и мы.

Если знать все правила, отвечающие за движение объекта в пространстве-времени, а также начальные условия и все силы, действующие между объектом и остальной частью системы, можно предсказать, как он будет двигаться сквозь пространство и время. Но местоположение объекта нельзя указать точно, не добавив к пространственным координатам временную.
А это важно, поскольку если вы хотите, чтобы все вещи во Вселенной делали что-то друг с другом – взаимодействовали, связывались, формировали структуры, передавали энергию – нужно, чтобы существовал способ это делать. Представьте себе пьесу, в которой все персонажи прописаны, актёры готовы их играть, костюмы подготовлены, все строки прописаны и выучены. Недостаёт лишь одной, но очень важной вещи – сцены.
Что играет роль сцены в физике?
До появления Эйнштейна сцену обустраивал Ньютон. Всех «актёров» Вселенной можно было описать набором координат – местоположением в трёхмерном пространстве и моментом во времени. Всё было похоже на решётку декартовых координат – трёхмерную структуру с осями x, y и z, где у каждого объекта может быть импульс, описывающий его движение в пространстве как функция от времени. Само время считалось линейным, идущим с неизменной скоростью. В представлении Ньютона пространство и время были абсолютными.

Мы часто представляем себе пространство в виде трёхмерной решётки, хотя это чрезмерное упрощение, зависящее от системы отсчёта. На самом деле пространство-время искривляется в присутствии материи и энергии, а расстояния в нём не фиксированы, а изменяются с расширением или сжатием Вселенной
Однако открытие в конце XIX века радиоактивности бросило на картину мира Ньютона тень сомнений. Узнав, что атомы могут испускать субатомные частицы, движущиеся со скоростью света, мы поняли нечто удивительное: когда частица движется со скоростью, близкой к скорости света, она воспринимает пространство и время совершенно не так, как объект, движущийся медленно или покоящийся.
Нестабильные частицы, очень быстро распадающиеся в состоянии покоя, жили тем дольше, чем ближе их скорость была к скорости света. Эти частицы проходили расстояния большие, чем должны были, исходя из их скорости и времени жизни. А при попытке подсчитать энергию или импульс движущейся частицы разные наблюдатели (движущиеся с разными скоростями относительно неё) получали несовпадающие значения.
Получается, что с концепцией пространства-времени от Ньютона что-то было не так. На скоростях, близких к скорости света время удлиняется, расстояния сжимаются, а энергия и импульс зависят от системы отсчёта. То есть, ваше восприятие Вселенной зависит от того, как вы двигаетесь.

Световые часы, в которых протон отражается от двух зеркал, могут отсчитывать время для любого наблюдателя. И хотя двое наблюдателей могут не сойтись во мнении о том, сколько времени прошло между двумя моментами, они могут договориться о законах физики и константах Вселенной, в частности, о скорости света. У неподвижного наблюдателя время идёт как обычно, а у быстро движущегося часы будут идти медленнее, чем у неподвижного.
Эйнштейн отвечает за выдающийся прорыв в концепции реальности, описывавшей, какие величины не меняются при движении наблюдателя, а какие зависят от системы отсчёта. К примеру, скорость света одинакова для всех наблюдателей, как и масса покоя любого количества материи. А вот расстояние между двумя точками сильно зависит от вашего движения вдоль линии, их соединяющей. Скорость, с которой идут ваши часы, также зависит от вашего движения.
Пространство и время оказались не абсолютными, как думал Ньютон, и воспринимались разными наблюдателями по-разному. Они оказались относительными, поэтому теория и называется «теорией относительности». Более того, между восприятием неким наблюдателем пространства и времени есть определённая связь. Через пару лет после публикации Эйнштейном специальной теории относительности (СТО) её вывел его бывший профессор Герман Минковский. Он вывел единую математическую структуру, включающую пространство и время: пространство-время. Как писал он сам,
Отныне время само по себе и пространство само по себе становятся пустой фикцией, и только единение их сохраняет шанс на реальность.
Сегодня это пространство-время широко используется до сих пор, если можно пренебречь гравитацией: пространство Минковского.
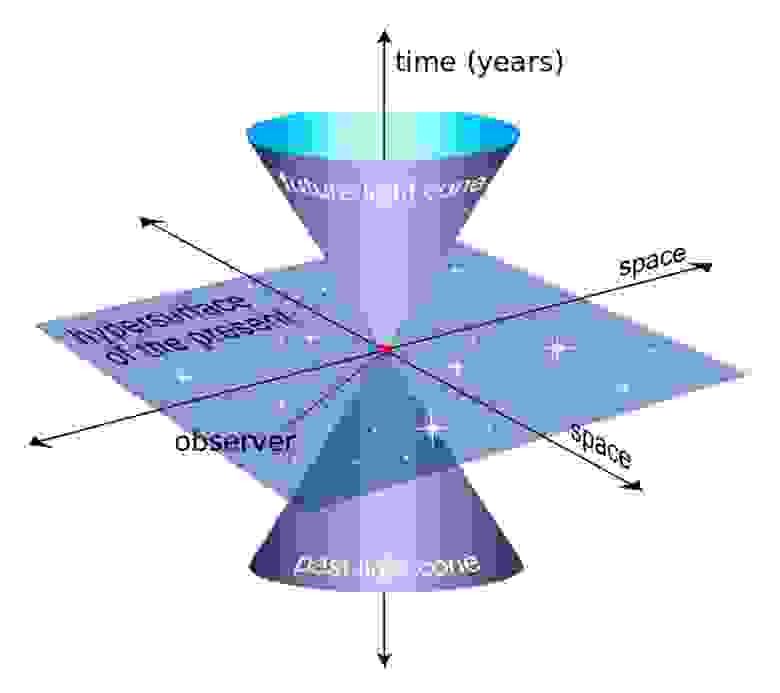
Световой конус, трёхмерная поверхность, составленная из всех возможных световых лучей, приходящих и исходящих из одной точки пространства-времени. Чем больше вы проходите в пространстве, тем меньше вы проходите во времени, и наоборот. Сегодня на вас может воздействовать только то, что было в световом конусе прошлого. В будущем вы сможете воспринять только те вещи, которые содержатся в вашем световом конусе будущего. Это иллюстрация плоского пространства Минковского, не искривлённого пространства ОТО.
Но в реальной Вселенной есть гравитация. Эта сила не действует мгновенно через огромные пространства космоса. Она распространяется с той же скоростью, что и все безмассовые кванты: со скоростью света. Все правила, сформулированные в СТО, остаются применимыми, но чтобы включить в картину гравитацию, требовалось нечто большее: представление о наличии у пространства-времени собственной кривизны, зависящей от присутствия в нём материи и энергии.
В каком-то смысле это просто: если вы разместили на сцене актёров, сцена должна выдерживать их вес. Если актёры массивные, а сцена не идеально жёсткая, она будет деформироваться в их присутствии.
То же явление работает и с пространством-временем: наличие материи и энергии искривляет его, а это искривление влияет на расстояния (пространство) и скорость хода часов (время). Более того, влияние это получается довольно сложным. Если вычислять влияние материи и энергии на пространство-время, то пространственные и временные эффекты оказываются связанными. Линии трёхмерной решётки, которую мы представляли в СТО, в ОТО искривляются.

Появление массы в пустой трёхмерной решётке заставляет её линии искривляться определённым образом. Они как бы вытягиваются в сторону массы.
Пространство-время можно представлять себе как чисто вычислительный инструмент, и остановиться на этом. В математике даже пространство-время можно описать метрическим тензором. Этот формализм позволяет вычислить, как любое поле, прямая, дуга, расстояние и т.п. могут существовать в нём определённым, точно описанным образом. Пространство может быть плоским или сколь угодно искривленным, конечным или бесконечным, открытым или закрытым, и состоять из любого количества измерений. В ОТО метрический тензор четырёхмерный (с тремя пространственными и одним временным измерением), а кривизну пространства-времени определяют материя, энергия и его внутренние напряжённости.
Проще говоря, кривизну пространства-времени определяет содержимое Вселенной. А затем можно взять кривизну пространства-времени и предсказать, как любая часть материи и энергии будет двигаться и меняться со временем. Правила ОТО позволяют нам предсказывать, как материя, свет, антиматерия, нейтрино и даже гравитационные волны будут двигаться сквозь Вселенную. Все эти предсказания прекрасно совпадают с нашими наблюдениями и измерениями.
Что мы не измеряем, так это само пространство-время. Мы можем измерять расстояния и временные интервалы – но всё это непрямое зондирование лежащего в их основе пространства-времени. Мы можем измерить всё, что с нами взаимодействует – тела, инструменты, детекторы – однако взаимодействие происходит только при наличии двух объектов в одной точке пространства-времени, когда при их встрече регистрируется «событие».
А также множество других воздействий. Однако из того, что мы можем измерять лишь воздействие пространства-времени на материю и энергию Вселенной, но не само пространство-время, следует, что пространство-время ведёт себя неотличимым от простого инструмента вычисления образом.

Квантовая гравитация пытается объединить ОТО Эйнштейна с квантовой механикой. Квантовые поправки к классической гравитации обозначаются в виде петлевых диаграмм, как та, что показана на рисунке белым цветом. Если расширить Стандартную Модель, включив в неё гравитацию, симметрия, описывающая CPT (симметрия Лоренца) может стать только приблизительной, могут появиться её нарушения. Однако пока что в экспериментах таких нарушений не наблюдалось.
Но это не значит, что пространство-время не является реальной физической сущностью. Наблюдая актёров, играющих пьесу, вы вправе назвать то место, где идёт пьеса, «сценой», будь то поле, платформа, голая земля и т.п. Даже если бы пьеса разыгрывалась в невесомости космоса, вы бы просто могли отметить, что в качестве сцены используется свободно падающая система отсчёта.
В физической Вселенной, насколько нам известно, невозможно существование объектов и взаимодействие между ними без пространства-времени. Где есть пространство-время, там работают законы физики, и существуют фундаментальные квантовые поля, лежащие в основе всего. В каком-то смысле, «ничто» – это вакуум пустого пространства-времени, а разговор о том, что происходит в отсутствии пространства-времени, не имеет смысла – по крайней мере, с точки зрения физики. Нет смысла говорить о «где», лежащем за границами пространства, и «когда», выходящем за границы времени. Возможно, что-то такое и существует, но физических концепций этой сущности у нас нет.

Анимация взаимодействия пространства-времени с массой, движущейся сквозь него. Из неё видно, что пространство-время – это не просто некая ткань. Всё трехмерное пространство искривляется в присутствии массы и энергии. Несколько вращающихся друг вокруг друга масс порождают гравитационные волны.
Самое интересное, что у нас есть ещё много вопросов о природе пространства-времени, оставшихся без ответа. Являются ли пространство и время квантовыми и дискретными, разделёнными на невидимые участки, или же они непрерывны? Является ли гравитация квантовым взаимодействием, как все остальные известные силы, или это классическая, непрерывная ткань, тянущаяся вплоть до планковских масштабов? Если пространство-время отличается от того, что говорит нам ОТО, то как именно, и каким образом мы можем это обнаружить?
Но, несмотря на всё то, что пространство-время позволяет нам предсказать и узнать, оно не является такой же реальной сущностью, как атом. Нельзя каким-то образом напрямую «обнаружить» пространство-время – обнаружить можно только отдельные кванты материи и энергии, существующие в вашем пространстве-времени. Мы описали пространство-время в виде ОТО Эйнштейна, и она успешно предсказывает и объясняет все физические явления, когда-либо обнаруженные и измеренные нами. Однако вопрос о том, что оно собой представляет, и реально оно или нет, для современной науки пока остаётся открытым.
Что такое пространство-время на самом деле?
Перевод поста Стивена Вольфрама «What Is Spacetime, Really?».
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации.
Примечание: данный пост Стивена Вольфрама неразрывно связан с теорией клеточных автоматов и других смежных понятий, а также с его книгой A New Kind of Science (Новый вид науки), на которую из этой статьи идёт большое количество ссылок. Пост хорошо иллюстрирует применение программирования в научной сфере, в частности, Стивен показывает (код приводится в книге) множество примеров программирования на языке Wolfram Language в области физики, математики, теории вычислимости, дискретных систем и др.
Содержание
Есть много различных моментов в теории, указывающих, что общая теория относительности — не последняя точка в истории о пространстве-времени. И в самом деле, пускай мне нравится ОТО как абстрактная теория, однако я пришел к мысли, что она, возможно, на целый век увела нас от пути познания истинной природы пространства и времени.
Я размышлял об устройстве пространства и времени немногим более сорока лет. В начале, будучи молодым физиком-теоретиком, я просто принимал эйнштейновскую математическую постановку задачи специальной и общей теории относительности, а так же занимался некоторой работой в квантовой теории поля, космологии и других областях, основываясь на ней.
Но около 35 лет назад, отчасти вдохновленный своим опытом в технических областях, я начал более детально исследовать фундаментальные вопросы теоретической науки, с чего и начался мой длинный путь выхода за рамки традиционных математических уравнений и использования вместо них вычислений и программ как основных моделей в науке. Вскоре после этого мне довелось выяснить, что даже очень простые программы могут демонстрировать очень сложное поведение, а затем, спустя годы, я обнаружил, что системы любого вида могут быть представлены в терминах этих программ.
Воодушевившись этим успехом, я стал размышлять, может ли это иметь отношение к важнейшему из научных вопросов — физической теории всего.
Во-первых, такой подход казался не слишком перспективным — хотя бы потому, что модели, которые я изучал (клеточные автоматы), казалось, работали так, что это полностью противоречило всему тому, что я знал из физики. Но где-то в 88-м году — в то время, когда вышла первая версия Mathematica, я начал понимать, что если бы я изменил свои представления о пространстве и времени, возможно, это к чему то бы меня привело.
Простая теория всего?
Из статьи вовсе не кажется очевидным, что теория всего для нашей вселенной должна быть проста. И в самом деле, история физики привносит дополнительные сомнения, ведь чем больше мы узнаем, тем вещи оказываются более сложными, во всяком случае, в терминах математического аппарата, вводимого ими. Но, как отмечалось, к примеру, богословами много веков назад, есть очевидная черта нашей вселенной — в ней есть порядок. Частицы нашей вселенной не просто подчиняются каким-то своим законам, но и подчиняются определённому набору общих законов.
Но насколько простой может быть теория всего для нашей Вселенной? Скажем, мы можем представить её в виде программы, допустим, в Wolfram Language. Насколько большой будет эта программа? Будет ли оно сравнима с длиной человеческого генома, или больше походить по объему на операционную систему? Или же она будет значительно меньше?
Если бы я отвечал на этот вопрос до того, как начал исследовать вычислительную вселенную простых программ, я бы, скорее всего, ответил, что подобная программа должна быть чем то весьма сложным. Однако мне удалось обнаружить, что в вычислительной вселенной даже чрезвычайно простые программы могут демонстрировать сколь угодно сложное поведение (этот факт отражен в общем принципе вычислительной эквивалентности).
Структура данных Вселенной
Но какой должна быть такая программа? Ясно одно: если программа и вправду может быть чрезвычайно простой, то она будет слишком мала для того, чтобы в явной форме кодировать некоторые очевидные особенности нашей Вселенной, такие как массы частиц, разного рода симметрию, или даже пространственную размерность. Все эти вещи должны появляться каким-то образом из чего-то более низкоуровневого и фундаментального.
Но если поведение вселенной определяются простой программой, то какова структура данных, с которыми эта программа работает? Сперва я предположил, что это должно быть нечто простое для описания, как, к примеру, структура клеток, которая появляется в клеточном автомате. Но даже если подобная структура хорошо работает для описания моделей различных вещей, представляется, что она должна быть весьма неправдоподобной для фундаментальных физических моделей. Да, можно найти такие правила, что будут демонстрировать поведение, которое в большом масштабе не будет показывать очевидное свойства структуры. Однако если физика действительно может описываться некоторой простой моделью, то представляется, что столь жёсткая структура для пространства не может быть в неё включена, и что свойства пространства должны из чего-то проистекать.
Так какова альтернатива? Нам потребуется более низкоуровневое понятие, чем пространство, из которого оное и будет рождаться. Также нам потребуется базовая структура данных, которая будет максимально гибкой. Я размышлял об этом много лет, изучая самые разнообразные вычислительные и математические формальные системы. Но в конце концов я понял, что по сути все, с чем я сталкивался, может быть представлено одним способом — с помощью сетей.
Сеть — она же граф — состоит из некоторого количества узлов, которые соединены связями. И все свойства графа следуют из структуры этих связей.
Пространство как граф
Так может ли пространство состоять из чего-то подобного? В классической физике и ОТО пространство не представляется как состоящее из чего бы то ни было. Оно представляется в виде некоторой математической конструкции, которая служит чем-то вроде сцены, на которой имеется непрерывный диапазон возможных положений, занимаемых разными объектами.
Но что, если пространство — вероятно, в планковских масштабах — есть лишь старый добрый граф, лишённый квантовых свойств? Звучит не особо впечатляюще, однако для задания подобного графа требуется значительно меньше информации — достаточно просто сказать, какие узлы с какими соединены.
Но как подобное может порождать пространство? Прежде всего, откуда на больших масштабах возникает видимая непрерывность пространства? На самом деле, всё очень даже просто: это может быть следствием большого количество узлов и связей. Немного напоминает то, что происходит в жидкостях — скажем, в воде. В малых масштабах мы можем наблюдать молекулы, мечущиеся в тепловом движении. Однако масштабный эффект заставляет все эти молекулы порождать то, что мы воспринимаем как непрерывную жидкость.
Так получилось, что в середине 80-х я много времени уделял изучению этого феномена — это было частью моей работы, в которой я разбирался в природе кажущейся случайности турбулентных потоков жидкости. В частности, мне удалось показать, что если представить молекулы как клетки клеточного автомата, то их крупномасштабное поведение будет точно описываться дифференциальными уравнениями для потоков жидкости.
И потому, когда я начал размышлять о возможности существования подструктуры пространства, которое можно представить в виде сети, мне подумалось, что здесь можно использовать те же методы, и что это может свести уравнения ОТО Эйнштейна к другим, существенно более низкоуровневым.
Может быть, нет ничего, кроме пространства
Хорошо. Допустим, пространство есть сеть. Но что можно сказать обо всех вещах, располагаемых в пространстве? Что можно сказать об электронах, кварках, протонах и прочем? Стандартные физические представления говорят о том, что пространство есть сцена, на которой располагаются частицы, струны или что бы то ни было. Однако подобное представление становится весьма сложным. Но есть и более простой вариант: возможно, всё в нашей вселенной состоит из пространства.
В последние годы своей жизни Эйнштейн был весьма увлечен этой идеей. Он полагал, что, быть может, такие частицы, как электроны, можно рассматривать как нечто вроде черных дыр, что состоят из одного лишь пространства. Однако, опираясь лишь на формализм ОТО, Эйнштейн не смог развить эту идею, в результате чего она была заброшена.
И, так уж было, что за сотню лет до этого в умах некоторых людей жили подобные идеи. Это были времена до СТО, когда люди думали, что пространство заполнено средой, подобной жидкости — эфиром (по иронии судьбы в настоящее время мы вернулись к модели заполненного пространства — полем Хиггса, квантовыми флуктуациями в вакууме и прочим). Между тем, было понятно, что существуют различные типы атомов, соответствующие различным химическим элементам. И было выдвинуто предположение (в частности, Кельвином), что разным атомам можно сопоставить различные узлы эфира.
Это интересная идея, хоть и неправильная. Но, представляя пространство как сеть, можно рассмотреть схожую идею: возможно, частицы соответствуют определенным структурам сети. Быть может, всё сущее во вселенной есть сеть, а материи соответствуют какие-то структуры этой сети. Подобные вещи легко можно обнаружить на поле клеточного автомата. Даже если каждая клетка подчиняется некоторым простым правилам, в системе появляются определенные структуры со своими свойствами — прямо как частицы с физикой взаимодействия друг с другом.
То, как всё это может реализовываться на сетях — отдельная и очень большая тема. Однако сперва нам стоит обсудить одну очень важную вещь — время.
Что есть время?
В 19-ом веке были понятия пространства и времени. Оба описывались координатами, а с помощью некоторых математических формализмов появлялись схожим путем. Однако мысль о том, что пространство и время в некотором роде есть одно и то же, не была в ходу. Но потом появился Эйнштейн с ОТО, и люди начали говорить о пространстве-времени, в котором пространство и время есть грани некоего единого понятия.
Оно вносит множество смыслов в СТО, в которой, к примеру, перемещение с переменной скоростью есть суть вращение в четырехмерном пространстве-времени. И весь этот век физики полагали пространство-время некоей сущностью, в которой пространство и время не имеют фундаментальных различий.
Но как всё это будет работать в контексте сетевой модели пространства? Конечно, можно ввести четырёхмерную сеть, в которой время будет работать так же, как и пространство. А потом просто сказать, что нашей вселенной соответствует некоторая пространственно-временная сеть (или семейство сетей). Каждая сеть должна определяться некоторыми ограничениями: наша вселенная обладает такими и такими свойствами, и, получается, удовлетворяет таким и таким уравнениям. Однако это представляется неконструктивным подходом — он не говорит о том, как вселенная ведет себя, а лишь о том, что если что-то обладает таким-то поведением, то это что-то может быть вселенной.
И, к примеру, в контексте программ пространство и время проявляются весьма по-разному. В клеточных автоматах, к примеру, клетки располагаются в пространстве, однако поведение системы возникает в пошаговых изменениях времени. Но вот какой момент: из того, что низкоуровневые правила сильно разграничивают поведения пространства и времени, не следует, что на больших масштабах они не будут вести себя схожим образом — как и полагается в современной физике.
Формирование сети
Итак, давайте предположим, что сеть есть подпространственная структура. Как эта сеть формируется? Можно ввести простую гипотезу, которая заключается в том, что существует некое местное правило, которое говорит, что если вы видите некоторый фрагмент сети, выглядящий некоторым образом, то его следует заменить на фрагмент, который выглядит так.
Но теперь все становится немного сложнее. Ведь может быть много мест в сети, где можно применить подобное правило. Так что определяет порядок обработки каждого фрагмента?
По сути, каждое возможное упорядочение соответствует своему временному потоку. И можно было бы вообразить теорию, в которой все потоки имеют место быть, и наша вселенная имеет множественную историю.
Но мы можем обойтись и без этой гипотезы. Вместо этого, вполне возможно, существует лишь одна нить времени — и это хорошо соотносится с тем, что мы знаем о мире, с нашим опытом. И чтобы понять это, нам следует сделать нечто наподобие того, что сделал Эйнштейн, формулируя СТО: нам следует ввести более реалистичную модель того, чем может являться наблюдатель.
Излишне говорить, что какой-либо реальный наблюдатель должен иметь возможность существовать в нашей вселенной. Таким образом, если вселенная представляет собой сеть, то наблюдатель должен быть некоей частью этой сети. Вспомним теперь о постоянных небольших изменениях, которые происходят в сети. Чтобы знать, что подобное изменение (обновление) произошло, наблюдатель и сам должен быть изменен (обновлен).
Если вы проведете всю эту мысленную цепочку, которую я провел в книге A New Kind of Science (NKS), то поймете, что единственное, что могут воспринимать наблюдатели в истории вселенной — причинную сеть — то, когда одно событие вызывает другое.
А потом выясняется, что есть определенный класс базисных правил, для которых различные порядки базисных обновлений не влияют на причинно-следственную сеть. Их я называю «причинно-следственно инвариантными» правилами.
Причинная инвариантность является интересным свойством, которое имеет аналоги в различных вычислительных и математических системах, например в том, что преобразования в алгебре могут быть применены в любом порядке и будут давать один и тот же конечный результат. Но в контексте вселенной его следствием является то, что он гарантирует, что есть только один поток времени во вселенной.
Вывод СТО
Так что насчёт пространства-времени и СТО? Тут, как я понял в середине 90-х, происходит нечто захватывающее: если есть причинно-следственная инвариантность, то из этого следует, что на больших масштабах СТО будет появляться сама собой. Другими словами, даже если на самом низком уровне пространства и времени всё происходит совсем по-другому, то в большем масштабе всё это порождает то, что предписывает СТО.
Грубо говоря, системы отсчета в специальной теории относительности — связанные, например, с перемещениями при разных скоростях — соответствуют различным последовательностям низкоуровневых изменений сети. Но из-за причинной инвариантности общее поведение, ассоциированное с различными последовательностями, получается точно таким-же — таким образом, система удовлетворяет принципам СТО.
В начале данная ситуация могла бы показаться безнадежной: как может сеть, которая рассматривает пространство и время по-разному, сойтись со СТО? Но это работает. И в самом деле, я не знаю никакой другой модели, которая может успешно вывести принципы СТО из чего-то более низкоуровневого; в современной физике это всегда представлялось как данность.
Вывод ОТО (Общей теории относительности)
Ок, СТО можно получить из простых моделей, основанных на сетях. Но что можно сказать об ОТО? Есть очень хорошая новость: опираясь на различные предположения, в конце 90-х мне удалось вывести уравнения Эйнштейна из динамики сетей.
Вся эта история в действительности несколько сложнее, но вот примерный пересказ. Во-первых, нам стоит вообразить, как сеть формирует из себя пространство. Следует помнить, что сеть есть лишь набор узлов и связей. Притом узлы могут располагаться в одномерном, двумерном или любом n-мерном пространстве.
Тут много математических сложностей. Следует рассмотреть кратчайшие пути — геодезические линии сети. Следует понять, как сделать что бы то ни было не только в пространстве, но и на сети с течением времени. Так же следует понять то, до каких масштабов проявляются свойства сети.
При выводе математических результатов важно иметь возможность получать разного рода средние значения. По сути, это подобно выведению уравнений для жидкости из динамики молекул: нужно иметь возможность принимать среднее из некоторого диапазона случайных значений в низкоуровневых взаимодействиях.
Но хорошая новость заключается в том, что существует необъятное количество систем, построенных даже на чрезвычайно простых правилах, которые подобны цифрам числа пи, то есть для любых прикладных целей являются достаточно случайными. Получается, что даже если особенности причинной сети полностью определены для того, кто знает исходное состояние сети, то большая часть этих особенностей будут являться, по сути, случайными.
Вот что имеем в итоге. Если ввести предположение об эффективной микроскопической случайности и предположить, что поведение системы в целом не приводит к изменению во всех ограничивающих размерностях, то из этого следует, что масштабное поведение системы удовлетворяет уравнениям Эйнштейна!
Полагаю, это очень интересно. Уравнения Эйнштейна можно получить практически из ничего. Это означает, что эти простые сети воспроизводят черты гравитации, которые мы знаем из современной физики.
Есть ряд деталей, которые не подходят под формат этой статьи. Многие из них я озвучивал довольно давно в NKS, особенно в заметках в конце.
Некоторые из вещей, возможно, стоит упомянуть. Во-первых, стоит отметить, что эти базисные сети не только представляются в обычном непрерывно определенном пространстве, но и не определяют такие топологические понятия, как внутри и снаружи. Все эти понятия являются следствием и выводятся.
Когда дело доходит до вывода уравнений Эйнштейна, тензоры Риччи рождаются из геодезических линий на сети вместе с ростом сфер, которые берут начало из каждой точки на геодезической линии.
Полученные уравнения Эйнштейна являются уравнениями Эйнштейна для вакуума. Но как и в случае с гравитационными волнами, можно эффективно отделить особенности пространства, связанные с материей, а затем получить полные уравнения Эйнштейна в терминах материи-энергии-импульса.
Когда я пишу это, то понимаю, насколько легко скатываюсь к «языку физиков» (вероятно, это связано с тем, что я занимался физикой в молодости. ). Но достаточно просто сказать, что на высоком уровне появляется захватывающая вещь, которая заключается в том, что из простой идеи о сетях и причинно-следственно инвариантных правил замены можно вывести уравнения ОТО. Сделав удивительно мало, мы получаем яркую звезду физики 20-го века: общую теорию относительности.
Частицы, квантовая механика и прочее
Весьма здорово — иметь возможность вывести ОТО. Но на этом физика не заканчивается. Другой очень важной её частью является квантовая механика. Боюсь, я не смогу в рамках этой статьи подробно развернуть эту тему, но, по-видимому, такие частицы, как электроны, кварки или бозоны Хиггса должны представляться в виде некоторых особых областей сети. В качественном смысле они могут не сильно отличаться от «эфирных узлов» Кельвина.
Но тогда их поведение должно следовать правилам, которые мы знаем из квантовой механики — или, если более конкретно — из квантовой теории поля. Ключевой особенностью квантовой механики является то, что она может быть сформулирована в терминах множественных поведений, каждое из которых связано с определенной квантовой амплитудой. Я не до конца со всем этим разобрался, однако есть намек на то, что нечто подобное происходит, если смотреть на эволюцию сети с различными возможными последовательностями низкоуровневых замен.
Моя сетевая модель, говоря строго, не имеет никаких квантовых амплитуд. Она больше похожа (но не в точности) на классическую, по сути, вероятностную модель. И в течение полувека люди считали, что с подобными моделями сопряжены практически нерешаемые проблемы. Ведь есть такая теорема Белла, в которой говориться, что если нет мгновенных нелокальных распространений информации, то не найдется и такой модели «скрытых переменных», что сможет воспроизвести квантово-механические результаты, наблюдаемые экспериментально.
Но есть принципиальные замечания. Вполне себе ясно, что означает нелокальность в обычном пространстве некоторой размерности. Но что можно сказать в контексте сетей? Тут всё по-другому. Потому что все определяется одними лишь связями. И хоть сеть и может в больших масштабах представляться трехмерной, остаётся возможность, что есть некие «нити», соединяющие некоторые области, которые без оных были бы отделены друг от друга. И мне не даёт покоя одна мысль — есть основания полагать, что эти нити могут генерироваться подобными частицам структурами, распространяющимися в сети.
В поисках вселенной
Хорошо, получается, что некоторые модели на основе сетей могут воспроизвести модели современной физики. Но с чего стоит начать поиск модели, в точности воспроизводящей нашу вселенную?
Первая мысль — начать с существующей физики и попытаться адаптировать инженерно-прикладные правила так, чтобы воспроизвести её. Но единственный ли это путь? А что если просто начать перечислять все возможные правила, ища среди них те, что будут описывать нашу вселенную?
Не начав изучение вычислительной вселенной простейших программ, я бы подумал, что это безумная затея: правила нашей вселенной никак не могут быть достаточно простыми для того, чтобы их можно было бы найти простым перечислением. Но увидев, что творится в вычислительной вселенной и увидев некоторые другие примеры, в которых потрясающие вещи были найдены одним лишь перебором, я понял, что ошибаюсь.
Но что будет, если кто-то действительно начнет осуществлять подобный поиск? Вот подборка сетей, полученных после довольно небольшого числа шагов, используя все возможные правила определенного, весьма простого типа:
Некоторые из этих сетей явно не соответствуют нашей вселенной. Они просто замирали спустя несколько итераций, то есть время в них, по сути, останавливалось. Или структура их пространства была слишком простой. Или у них было бесконечное число измерений. Или какие-то другие проблемы.
Здорово, что с такой удивительной быстротой мы можем найти те правила, которые явно не соответствуют нашей вселенной. А сказать то, что именно этот объект — наша вселенная, является значительно более сложной задачей. Потому что даже если смоделировать большое количество шагов, то невероятно сложно будет показать то, что поведение этой системы демонстрирует то же самое, что говорят нам физические законы о ранних моментах жизни вселенной.
Хотя есть ряд обнадеживающих вещей. Например, эти вселенные могут рождаться с фактически бесконечным числом измерений, а затем постепенно сжиматься до конечного числа измерений, потенциально устраняя необходимость в явной инфляции в ранней Вселенной.
А если рассуждать на более высоком уровне, то следует помнить, что если использовать весьма простые модели, то будет иметь место большое расстояние между «соседними моделями», так что, скорее всего, эти модели будут либо точно воспроизводить известные физические построения, либо будут далеки от истины.
В конце концов, нужно воспроизвести не только правила, но и начальное состояние вселенной. И как только мы узнаем его, то мы принципиально сможем узнать точную эволюцию вселенной. Так означает ли это, что можно было бы сразу узнать все о вселенной? Однозначно нет. Из-за явления, которое я называю «вычислительной несводимостью», и которое подразумевает, что если знать правила и начальное состояние для системы, она по-прежнему может требовать неприводимое количество вычислительной работы для прослеживания каждого шага системы в выяснения того, что она делает.
Тем не менее, существует вероятность, что кто-то сможет найти простое правило и начальное состояние, сказав: «Смотрите-ка, это наша вселенная!» Мы нашли бы нашу вселенную в пространстве всех возможных вселенных.
Конечно, это было бы знаменательным днём для науки.
Но возникло бы множество других вопросов. Почему именно это правило, а не другое? И почему наша Вселенная должна иметь правило, которое появляется достаточно рано в нашем списке всех возможных вселенных, и которое мы можем найти простым перечислением?
Можно было бы подумать, что именно особенности нашей вселенной и тот факт, что мы в ней находимся, заставят нас сформировать правила перечисления так, что вселенная появится достаточно рано. Но в настоящее время я полагаю, что всё должно быть значительно более экстравагантно, как, например, в случае с наблюдателем во вселенной — все из большого класса нетривиальных возможных правил для вселенных в действительности эквивалентны, потому можно выбрать любое из них и получить точно такие же результаты, просто по-другому.
Ок, покажите мне Вселенную
Но всё это лишь догадки. И пока мы и в самом деле не найдем кандидата на правило нашей вселенной, вероятно, на обсуждение этих вещей не стоит тратить много времени.
Так, хорошо. Какова наша текущая позиция во всем этом? Большую часть из того, что сейчас обсуждалось, я понял где-то в 99-ом — за несколько лет до окончания A New Kind of Science. И хоть я и писал на простом языке, а не в формате статьи по физике, мне удалось покрыть основные моменты этой темы в девятой главе книги, добавив некоторые технические детали в примечаниях в конце.
Но после того, как в 2002 году книга была закончена, я снова начал работать над физическими проблемами. Будет забавным сказать, что в моём подвале стоял компьютер, который искал фундаментальную физическую теорию. Но вот что на самом деле он делал: перечислял возможные правила различных типов и пытался обнаружить соответствие их поведения определенным критериям, которые могли бы сделать их правдоподобными в качестве моделей физики.
Я весьма скрупулёзно проделывал это работу, черпая идеи из простых случаев, последовательно продвигаясь к более реалистичным. Было много технических вопросов. Как представлять большие эфолюционирующие последовательности графов. Или как быстро распознавать слабоуловимые закономерности, которые показывают, что правило не соответствует нашей вселенной.
Работа разрослась на тысячи страниц, если её представлять в печатной форме, постепенно приближая к пониманию основ того, что могут делать системы, основанные на сетях.
В некотором смысле это было чем-то вроде хобби, которым я занимался параллельно с текучкой по управлению компанией и ее технологическим развитием. И был еще один отвлекающий фактор. В течение многих лет я занимался проблемой вычислительных знаний и построением движка, который мог бы всесторонне их реализовывать. И по результатам моей работы над A New Kind of Science я убедился, что это возможно, и что сейчас подходящее время для реализации этого.
К 2005 году стало ясно, что это действительно возможно реализовать, и потому я решил посвятить себя этому направлению. В результате получилась Wolfram|Alpha. И как только Wolfram|Alpha была запущена, то стало ясно, что можно сделать значительно большее — и я посвятил своё, пожалуй, наиболее продуктивное десятилетие на создание огромной системы из идей и технологий, которая дала возможность реализовать Wolfram Language в его нынешнем виде, а так же множество других вещей.
Заниматься физикой или нет — вот в чем вопрос
Но в течение этого десятилетия я не занимался физикой. И когда сейчас я смотрю на файловую систему на своем компьютере, я вижу большое количество ноутбуков с материалами по физике, сгруппированные с полученными мною результатами, и все это оставалось брошенным и нетронутым с начала 2005 года.
Должен ли я вернуться к вопросам физики? Я определенно хочу этого. Хотя есть и другие вещи, которые я хотел бы реализовать.
Я провел большую часть своей жизни, работая над очень большими проектами. И я упорно трудился, планируя то, что собираюсь сделать, пытаясь их распланировать на ближайшее десятилетие. Иногда я откладывал проекты, потому что существующие на тот момент технологии или инфраструктура были ещё не готовы к ним. Но как только я приступал к работе над проектом, я давал себе обещание найти способ его успешно завершить, даже если для его реализации потребуется много лет напряженной работы.
Однако поиск фундаментальной физической теории, пожалуй, несколько отличается от проектов, над которыми мне приходилось работать раньше. В некотором смысле критерии его успеха гораздо жестче: он или решает проблему и находит теорию, или нет. Да, можно было бы найти множество интересных абстрактных понятий из формирующийся теории (как в теории струн). И вполне вероятно, что такое исследование даст интересные побочные результаты.
Но в отличие от создания технологий или исследования научных областей, формулирование содержания этого проекта вне нашего контроля. Его содержание определяется нашей вселенной. И, вполне возможно, я просто ошибаюсь в предположениях о том, как работает наша вселенная. Или, быть может, что я прав, но есть практически непреодолимый барьер из-за вычислительной несводимости, который лишает нас возможностей познать эту сферу.
Кто-то может сказать, что есть вероятность того, что мы найдем некоторую вселенную, которая будет походить на нашу, но мы так никогда и не узнаем, наша ли она в действительности. Я, на самом деле, не особо беспокоюсь об этом. Я думаю, что есть достаточное количество аномалий в существующей физике, приписываемых таким вещам, как темная материя, объяснение которых даст нам полную уверенность в том, что мы нашли верную теорию. Будет здорово, если можно будет сделать предположение и быстро проверить его. Но к тому времени, как мы выведем все, казалось бы, произвольные массы частиц, и другие известные особенности физики, можно будет быть уверенным, что мы имеем дело с верной теорией.
Было занятно в течение многих лет спрашивать у своих друзей, должен ли я заниматься фундаментальными вопросами физики. И получал я три совершенно разных типа ответов.
Первый — простой: «Ты должен заниматься этим!» Они говорили, что проект является самым увлекательным и важным из тех, что можно себе вообразить, и не могут понять, зачем ждать ещё хоть один лишний день, прежде чем к нему приступить.
Второй тип ответов: «Зачем тебе этим заниматься?» Затем они говорят нечто вроде «Почему бы не решить проблему искусственного интеллекта, или молекулярной инженерии, биологического бессмертия, или, по крайней мере, не построить огромную многомиллиардную компанию? Зачем заниматься чем-то столь абстрактным и теоретическим, когда можно сделать что-то насущное и изменить тем самым мир?»
А есть третий тип ответов — весьма ожидаемый, если иметь в виду историю науки. В основном он исходит от моих друзей-физиков, и это некая комбинация из «Не трать своё время на это!» и «Пожалуйста, не надо этим заниматься«.
Дело в том, что нынешний подход к фундаментальной физике, основанный на теории квантового поля, насчитывает почти 90 лет. Он имел ряд успехов, однако не привел нас к фундаментальной физической теории. Но для большинства современных физиков нынешний подход и есть суть сама физика. И когда они слышат о том, над чем я работаю, им это кажется чем-то столь незнакомым, будто это на самом деле и не физика.
И некоторые из моих друзей прямо так и говорят: «Я надеюсь, что у тебя ничего не получится, потому что тогда все, над чем я работал, пойдет коту под хвост«. Ну, да, многое из сделанного окажется бессмысленным. Но вы всегда сталкиваетесь с этим риском, когда занимаетесь проектом, в котором природа решает что верно, а что нет. Но я должен сказать, что даже если можно будет найти по-настоящему фундаментальную физическую теорию, то останется ещё очень большое поле для работы квантовой теории поля, к примеру — объяснение различных эффектов на масштабах, с которыми мы работаем в настоящее время на ускорителях частиц.
Что требуется?
Так, хорошо, если я запущу проект по поиску фундаментальной физической теории, то что мне следует делать? Это сложный проект, которому потребуюсь не только я, но также и разнородная группа талантливых людей.
Будет ли он в конечном счете работать — не знаю, но думаю, что будет довольно интересно за ним наблюдать, и я планирую представить его в прозрачном формате, сделав его максимально доступным и познавательным (конечно, это будет ободряющим контрастом с тем режимом отшельника, в котором я работал над A New Kind of Science в течение десяти лет).
Безусловно, я не могу знать, насколько сложен этот проект, и принесет ли он вообще результаты. В конечном счете это зависит от того, какова есть на самом деле наша вселенная. Но, основываясь на том, что я сделал десять лет назад, у меня есть четкий план относительно того, с чего начать и каких людей свести вместе в рамках одной команды.
Тут потребуются как хорошие учёные, так и прикладники/инженеры. Потребуется проделать много работы в области разработки алгоритмов эволюции сетей и их анализа. Я уверен, что тут потребуется теория графов, современная геометрия, теория групп и, возможно, некоторые другие разделы абстрактной алгебры. И я не удивлюсь, если в итоге будут задействовано большое количество других областей математики и теоретической информатики.
Тут потребуется сложная и серьёзная физика, с понимаем основ квантовой теории поля, теории струн и, возможно, таких разделов, как спиновые сети. Также, вероятно, потребуются методы статистической физики и её современных теоретических основ. Потребуется понимание общей теории относительности и космологии. И, если дела идут хорошо, потребуется работа над большим количеством разнообразных физических экспериментов, а также их интерпретация.
Будут и технические проблемы — понять, к примеру, то, как проводить огромную вычислительную работу по сетям и визуализировать получаемые результаты. Но я подозреваю, что самые большие проблемы будут в строительстве здания новой теории и понимании того, что необходимо для изучения различных видов сетевых систем, которые я хочу исследовать. Будет не лишней поддержка из существующих ныне областей. Но, в конце концов, подозреваю, потребуется построение существенно новой интеллектуальной структуры, которая не будет похожа ни на что из того, что имеется сейчас.
Но пришло ли время?
Подходящее ли сейчас время для реализации подобного проекта? Может быть, следует подождать, пока компьютеры получат больше вычислительных возможностей. Или когда некоторые области математики продвинутся дальше. Или пока не будут получены ответы на еще несколько вопросов из физики.
Я не уверен. Но я и не вижу никаких непреодолимых препятствий, а лишь то, что на этот проект потребуются усилия и ресурсы. И кто знает: может быть, это окажется проще, чем мы думаем, и мы, оглядываясь назад, будем задаваться вопросом — почему этого никто не сделал ранее.
Одним из ключевых моментов, который привел к общей теории относительности 100 лет назад, заключался в том, что пятый постулат Евклида («параллельные линии никогда не пересекаются») может и не выполняться в реальной вселенной, давая возможность существования искривленного пространства. Но если мои подозрения о космосе и вселенной верны, то это означает, что на самом деле есть и более фундаментальная проблема в основаниях Евклида — в самых первых его определениях. Ведь если существует дискретная подпространственная сеть, то предположения Евклида о точках и линиях, которые могут занимать любые пространственные положения, попросту не верны.
ОТО — отличная теория, но мы уже знаем, что она не может быть окончательной. И теперь мы должны задаться вопросом — сколько пройдет времени, прежде чем мы придем к окончательной теории. Надеюсь, не слишком много. И я надеюсь, что ОТО отпразднует не слишком много юбилеев прежде, чем мы узнаем, что же есть пространство-время на самом деле.