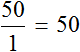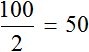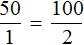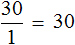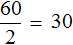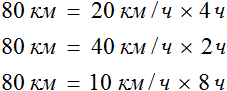Что значит пропорциональны числам

Пропорциональность

Значения, двух каких бы то ни было величин, могут взаимно зависеть друг от друга.

К примеру, площадь квадрата находится в зависимости от длины его стороны, и так же обратно, длина стороны квадрата зависима от его площади.

Две величины, которые по характеру являются взаимно зависимыми, называются пропорциональными, при условии, если отношение их значений будет неизменным.

Общий вес керосина пропорционален его настоящему объему, например:

2 л керосина весят 1,6 кг

5 л керосина весят 4 кг

7 л керосина весят 5,6 кг

Следовательно, отношение веса к его объему будет:

Отношение пропорциональных величин, являющихся неизменным, называются коэффициентом пропорциональности. Этот коэффициент пропорциональности указывает, сколько единиц одной взятой величины приходится на одну единицу другой.

Если две отдельные величины пропорциональны, то любая пара таких значений одной величины, будет образовывать пропорцию с парой соответствующих значений другой, выбранных в том же порядке.

Две величины, которые зависят друг от друга так, что при увеличении значения одной из них другая увеличивается в том, же соотношении, называются пропорциональными.

Две величины, которые зависят друг от друга так, что при увеличении одной величины другая в том же отношении будет уменьшаться, называются обратно пропорциональными.

Например, время пробега состава поезда между двумя отдельными станциями обратно пропорционально скорости этого поезда.

Если две, какие либо величины являются обратно пропорциональными, то любая пара значений одной величины формирует пропорцию с парой соответствующих значений величин другой, выбранных в обратном порядке, например:

Произведение значений двух обратно пропорциональных величин остаются неизменными.

Источник

Прямая и обратная пропорциональность

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз.

Пропорциональность бывает прямой и обратной. В данном уроке мы рассмотрим каждую из них.

Прямая пропорциональность

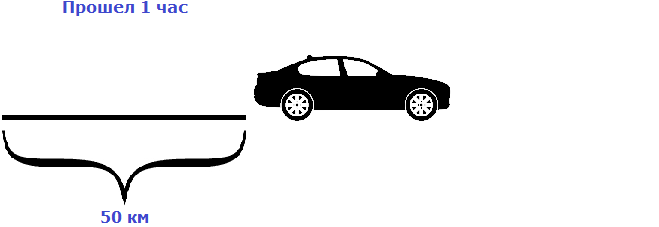
Предположим, что автомобиль двигается со скоростью 50 км/ч. Мы помним, что скорость это расстояние, пройденное за единицу времени (1 час, 1 минуту или 1 секунду). В нашем примере автомобиль двигается со скоростью 50 км/ч, то есть за один час он будет проезжать расстояние, равное пятидесяти километрам.

Изобразим на рисунке расстояние, пройденное автомобилем за 1 час

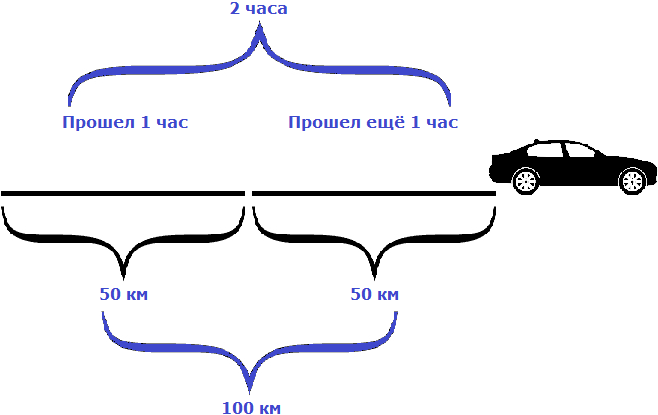
Пусть автомобиль проехал еще один час с той же скоростью, равной пятидесяти километрам в час. Тогда получится, что автомобиль проедет 100 км

Как видно из примера, увеличение времени в два раза привело к увеличению пройденного расстояния во столько же раз, то есть в два раза.

Такие величины, как время и расстояние называют прямо пропорциональными. А взаимосвязь между такими величинами называют прямой пропорциональностью.

Прямой пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.

и наоборот, если одна величина уменьшается в определенное число раз, то другая уменьшается во столько же раз.

Предположим, что изначально планировалось проехать на автомобиле 100 км за 2 часа, но проехав 50 км, водитель решил отдохнуть. Тогда получится, что уменьшив расстояние в два раза, время уменьшится во столько же раз. Другими словами, уменьшение пройденного расстояния приведет к уменьшению времени во столько же раз.

Интересная особенность прямо пропорциональных величин заключается в том, что их отношение всегда постоянно. То есть при изменении значений прямо пропорциональных величин, их отношение остается неизменным.

В рассмотренном примере расстояние сначала было равно 50 км, а время одному часу. Отношение расстояния ко времени есть число 50.

Но мы увеличили время движения в 2 раза, сделав его равным двум часам. В результате пройденное расстояние увеличилось во столько же раза, то есть стало равно 100 км. Отношение ста километров к двум часам опять же есть число 50

Число 50 называют коэффициентом прямой пропорциональности. Он показывает сколько расстояния приходится на час движения. В данном случае коэффициент играет роль скорости движения, поскольку скорость это отношение пройденного расстояния ко времени.

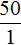
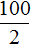
Из прямо пропорциональных величин можно составлять пропорции. К примеру, отношения и составляют пропорцию:

Это отношение можно прочитать следующим образом:

Пятьдесят километров так относятся к одному часу, как сто километров относятся к двум часам.

Пример 2. Стоимость и количество купленного товара являются прямо пропорциональными величинами. Если 1 кг конфет стоит 30 рублей, то 2 кг этих же конфет обойдутся в 60 рублей, 3 кг в 90 рублей. С увеличением стоимости купленного товара, его количество увеличивается во столько же раз.

Поскольку стоимость товара и его количество являются прямо пропорциональными величинами, то их отношение всегда постоянно.

Запишем чему равно отношение тридцати рублей к одному килограмму

Теперь запишем чему равно отношение шестидесяти рублей к двум килограммам. Это отношение опять же будет равно тридцати:

Здесь коэффициентом прямой пропорциональности является число 30. Этот коэффициент показывает сколько рублей приходится на килограмм конфет. В данном примере коэффициент играет роль цены одного килограмма товара, поскольку цена это отношение стоимости товара на его количество.

Обратная пропорциональность

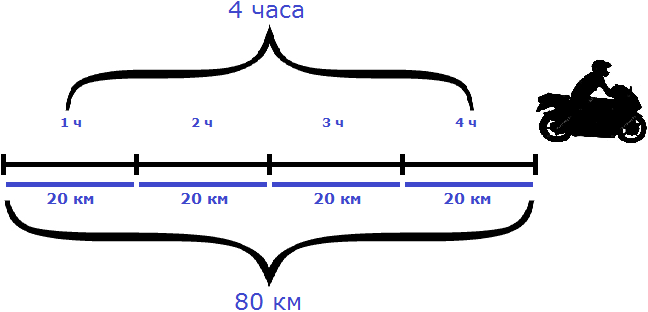
Рассмотрим следующий пример. Расстояние между двумя городами 80 км. Мотоциклист выехал из первого города, и со скоростью 20 км/ч доехал до второго города за 4 часа.

Если скорость мотоциклиста составила 20 км/ч это значит, что каждый час он проезжал расстояние равное двадцати километрам. Изобразим на рисунке расстояние, пройденное мотоциклистом, и время его движения:

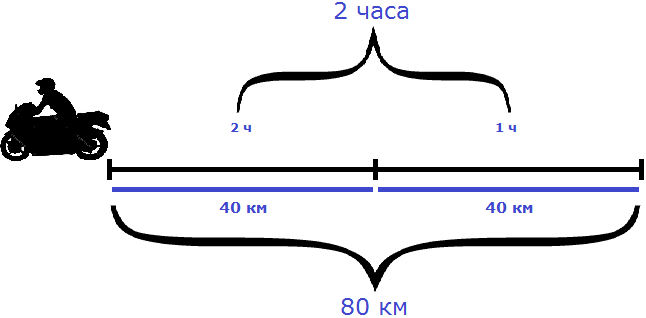
На обратном пути скорость мотоциклиста была 40 км/ч, и на тот же путь он затратил 2 часа.

Легко заметить, что при изменении скорости, время движения изменилось во столько же раз. Причем изменилось в обратную сторону — то есть скорость увеличилась, а время наоборот уменьшилось.

Такие величины, как скорость и время называют обратно пропорциональными. А взаимосвязь между такими величинами называют обратной пропорциональностью.

Обратной пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой уменьшение другой во столько же раз.

и наоборот, если одна величина уменьшается в определенное число раз, то другая увеличивается во столько же раз.

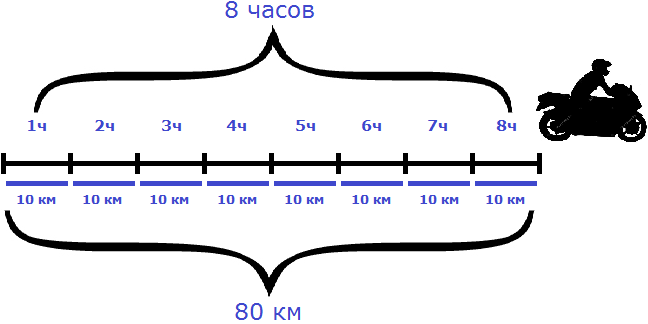
К примеру, если на обратном пути скорость мотоциклиста составила бы 10 км/ч, то те же 80 км он преодолел бы за 8 часов:

Как видно из примера, уменьшение скорости привело к увеличению времени движения во столько же раз.

Особенность обратно пропорциональных величин заключается в том, что их произведение всегда постоянно. То есть при изменении значений обратно пропорциональных величин, их произведение остается неизменным.

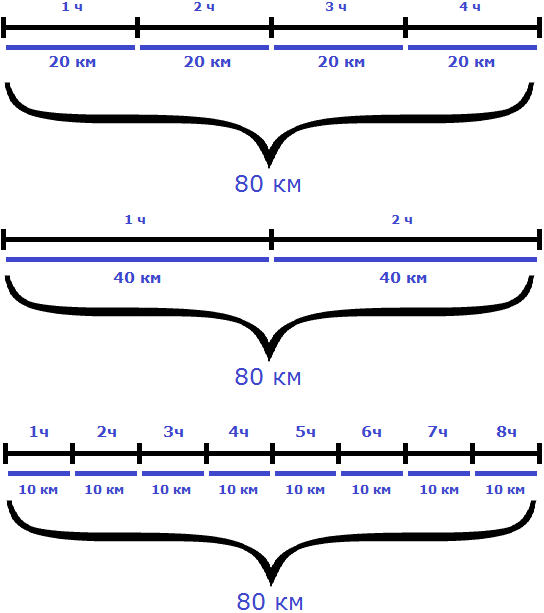
В рассмотренном примере расстояние между городами было равно 80 км. При изменении скорости и времени движения мотоциклиста, это расстояние всегда оставалось неизменным

Мотоциклист мог проехать это расстояние со скоростью 20 км/ч за 4 часа, и со скоростью 40 км/ч за 2 часа, и со скоростью 10 км/ч за 8 часов. Во всех случаях произведение скорости и времени было равно 80 км

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

10 thoughts on “Прямая и обратная пропорциональность”

что ценно теория методически верно преподается. очень добрый сайт.

мне теперь всё понятно, большое спасибо сайту

Источник

Прямая и обратная пропорциональность

Основные определения

Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.

Есть две разновидности пропорциональностей:

Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.

Прямо пропорциональные величины

Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.

Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».

a и d называются крайними членами, b и c — средними.

Свойство прямо пропорциональной зависимости:

Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

Примеры прямо пропорциональной зависимости:

Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.

Формула прямой пропорциональности

y = kx,

где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

Пример 1.

В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.

Пример 2.

Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?

Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.

Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.

Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:

Ответ: 20 человек напишут 420 постов за 12 дней.

Обратно пропорциональные величины

Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.

Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».

Свойство обратной пропорциональности величин:

Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.

Примеры обратно пропорциональной зависимости:

Формула обратной пропорциональности

где y и x — это переменные величины,

k — постоянная величина, которую называют коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента обратной пропорциональности:

Потренируемся

Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Соотношения равны, но перевернуты относительно друг друга.

Источник

Что такое пропорция

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Что такое пропорция

Пропорция — это равенство двух отношения.

Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.

Пропорция всегда содержит равные коэффициенты.

Если выразить определение формулой, то выглядеть оно будет так:

a и d — крайние члены пропорции

Читается это выражение так: a так относится к b, как c относится к d

Например:

Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.

15 и 3 — крайние члены пропорции.

5 и 9 — средние члены пропорции.

Наглядный пример для понимания:

У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.

Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!

А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.

Что мы имеем: 4 кусочка и 2 друга, претендующих на них.

Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.

Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.

Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным😉

Основное свойство пропорции

Запомните основное свойство пропорции:

Произведение крайних членов пропорции равно произведению средних членов этой пропорции.

В виде формулы свойство выглядит так:

a : b = c : d = a * d = b * c

Мы знаем, что a и d — крайние члены пропорции, b и c — средние.

Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.

Давайте проверим несколько пропорций.

Пример 1. Дана пропорция:6/2 = 12/4

Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.

Пример 2. Дана пропорция: 10/2 = 16/4

Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Примеры решения задач с пропорцией

Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.

Задачка 1. Дана математическая пропорция: 15/3 = x/4

Ответ: в пропорции 15/3 = x/4, x = 20

Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.

Ответ: четвертый член пропорции — 12.

Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?

Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.

Задачка 4. Дана пропорция: 20/2 = y/4

Источник

Пропорциональность

Содержание

Пример

Масса керосина пропорциональна его объёму: 2 л керосина имеют массу 1,6 кг, 5 л имеют массу 4 кг, 7 л имеют массу 5,6 кг. Отношение массы к объёму всегда будет равно плотности:

1,6 / 2 = 0,8; 4 / 5 = 0,8; 5,6 / 7 = 0,8 и т. д.

Коэффициент пропорциональности

Символ

Математический символ ‘∝’ используется для указания пропорциональности двух величин. Пример, A ∝ B.

В юникоде для отображения используется символ U+221D.

Прямая пропорциональность

Прямая пропорциональность — функциональная зависимость, при которой некоторая величина зависит от другой величины таким образом, что их отношение остаётся постоянным. Иначе говоря, эти переменные изменяются пропорционально, в равных долях, то есть, если аргумент изменился в два раза в каком-либо направлении, то и функция изменяется тоже в два раза в том же направлении.

Математически прямая пропорциональность записывается в виде формулы:

Графиком прямой пропорциональности является прямая линия, проходящая через начало координат.

Обратная пропорциональность

Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины(аргумента) вызывает пропорциональное уменьшение зависимой величины(функции).

См. также

Источники

Полезное

Смотреть что такое «Пропорциональность» в других словарях:

ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, пропорциональности, мн. нет, жен. (книжн.). 1. отвлеч. сущ. к пропорциональный. Пропорциональность частей. Пропорциональность телосложения. 2. Такая зависимость между величинами, когда они пропорционально (см. пропорциональный … Толковый словарь Ушакова

ПРОПОРЦИОНАЛЬНОСТЬ — (от лат. proportionalis соразмерный, пропорциональный). Соразмерность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПРОПОРЦИОНАЛЬНОСТЬ отлат. proportionalis, пропорциональный. Соразмерность. Объяснение 25000… … Словарь иностранных слов русского языка

Пропорциональность — 1) соразмерность элементов и их связей в одной системе; 2) принцип организации политических систем и процессов, динамическая сбалансированность политической системы. В политологическом ракурсе «пропорциональность» подразумевает выяснение целого… … Политология. Словарь.

пропорциональность — соразмерность, соизмеримость; соответствие, стройность, гармоничность, рациональность, нормальность. Ant. непропорциональность, асимметрия Словарь русских синонимов. пропорциональность соразмерность Словарь синонимов русского языка. Практический… … Словарь синонимов

ПРОПОРЦИОНАЛЬНОСТЬ — (от латинского proportio соотношение), простейший вид функциональной зависимости. Различают прямую пропорциональность y=kx (например, путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т.е. S=vt) и обратную… … Современная энциклопедия

ПРОПОРЦИОНАЛЬНОСТЬ — простейший вид функциональной зависимости (см. Функция). Различают прямую пропорциональность. (y =kx) и обратную пропорциональность (y=k/x). Напр., путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т. е. S =vt… … Большой Энциклопедический словарь

Пропорциональность — (от латинского proportio соотношение), простейший вид функциональной зависимости. Различают прямую пропорциональность y=kx (например, путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т.е. S=vt) и обратную… … Иллюстрированный энциклопедический словарь

пропорциональность — ПРОПОРЦИОНАЛЬНОСТЬ, соразмерность ПРОПОРЦИОНАЛЬНЫЙ, соразмерный ПРОПОРЦИОНАЛЬНО, соразмерно, соответственно … Словарь-тезаурус синонимов русской речи

ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, и, жен. 1. см. пропорциональный. 2. В математике: такая зависимость между величинами, при к рой увеличение одной из них влечёт за собой изменение другой во столько же раз. Прямая п. (при к рой с увеличением одной величины… … Толковый словарь Ожегова

ПРОПОРЦИОНАЛЬНОСТЬ — англ. proportionality; нем. Proportionalitat. Простейший вид функциональной зависимости, фиксирующей соотношение между двумя величинами; показатель отношения исследуемой функции ко всему числу изучаемых случайностей. Antinazi. Энциклопедия… … Энциклопедия социологии

ПРОПОРЦИОНАЛЬНОСТЬ — (лат. proportionalis) соблюдение пропорций, рациональных структурных соотношений в экономике, согласованное развитие отраслей, сфер, регионов. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр. М … Экономический словарь

Источник