Что значит произвольная точка в геометрии
Точки, Прямые и Отрезки — Определения и Свойства
Вспомним определения точки и прямой:
Точка — это фигура в геометрии, не имеющая никаких
измеримых характеристик, кроме координат.
Прямая — это фигура в геометрии, которая не
имеет ни начала, ни конца.
Для изображения прямых на чертеже используют линейку, но
при этом можно изобразить только часть прямой, а вся прямая бесконечна.
Принято обозначать прямые малыми латинскими буквами, а точки —
большими латинскими буквами.
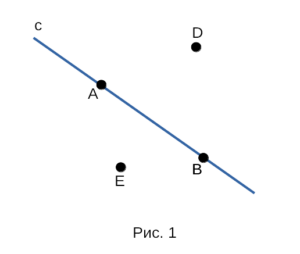
На рисунке 1 изображены прямая c и точки A, B, D, E. Точки А и B
лежат на прямой c, а точки D и E не лежат. Прямая с проходит через
точки A и B, но не проходит через точки С и D. Также заметим, что через
точки A и В нельзя провести другую прямую, не совпадающую с прямой c.
Через любые две точки можно провести прямую,
и притом только одну.
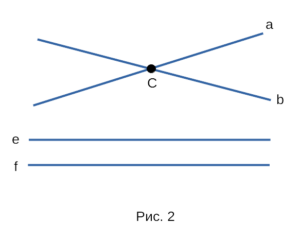
Если две прямые имеют общую точку, то можно сказать,
что они пересекаются. На рисунке 2 прямые a и b
пересекаются в общей точке C, а прямые e и f не
пересекаются, так как не имеют общей точки. Две прямые
не могут иметь двух и более общих точек, так как через две
и более точек проходит только одна прямая.
Две прямые имеют только одну общую точку,
либо не имеют общих точек.
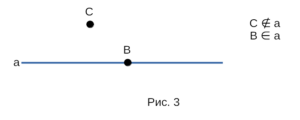
Прямую, на которой отмечены две точки, иногда обозначают двумя
буквами. Для обозначения того, лежит ли точка на прямой или нет,
используют математический символ ∈ или ∉. Пример использования
математического символа ∈ или ∉ на рисунке 3.
Часть прямой ограниченная двумя точками называется отрезком. Точки,
ограничивающие отрезок, называются концами отрезка. Отрезок имеет
начало и конец. Пример отрезка на рисунке 4.
произвольная точка
Смотреть что такое «произвольная точка» в других словарях:
Изолированная точка множества — Изолированная точка в общей топологии это такая точка множества, что пересечение некоторой её окрестности с множеством состоит только из этой точки. Содержание 1 Определение 2 Связанные определения … Википедия
Изолированная точка — в общей топологии это такая точка множества, что пересечение некоторой её окрестности с множеством состоит из единственной точки. Содержание 1 Определение 2 Связанные определения 3 Свойства … Википедия
КОНИЧЕСКИЕ СЕЧЕНИЯ — плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью, не проходящей через его вершину (рис. 1). С точки зрения аналитической геометрии коническое сечение представляет собой геометрическое место точек,… … Энциклопедия Кольера
МАТЕМАТИЧЕСКИЙ АНАЛИЗ — раздел математики, дающий методы количественного исследования разных процессов изменения; занимается изучением скорости изменения (дифференциальное исчисление) и определением длин кривых, площадей и объемов фигур, ограниченных кривыми контурами и … Энциклопедия Кольера
Линия — I Линия (от лат. linea) геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно. 1) В элементарной… … Большая советская энциклопедия
Линия (геометрич. понятие) — Линия (от лат. linea), геометрическое понятие, точное и в то же время достаточно общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии различно. 1) В элементарной геометрии рассматриваются… … Большая советская энциклопедия
ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО — совокупность двух объектов: множества X, состоящего из элементов произвольной природы, наз. точками данного пространства, и из введенной в это множество топологической структуры, или топологии, все равно открытой или замкнутой (одна переходит в… … Математическая энциклопедия
АБЕЛЕВ ДИФФЕРЕНЦИАЛ — голоморфный или мероморфный дифференциал на компактной, или замкнутой, римановой поверхности S(см. Дифференциал на римановой поверхности). Пусть g род поверхности S; а1b1 а 2b2. agbg циклы канонич. базиса гомологии S. В зависимости от характера… … Математическая энциклопедия
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия
Кривая Пеано — общее название для параметрических кривых, образ которых содержит квадрат (или, в более общем смысле, открытые области пространства) Содержание 1 Свойства 2 Примеры 3 Обобщения … Википедия
Прямая линия. Понятие прямой, ее свойства.
Наглядно прямую линию может продемонстрировать туго натянутый шнур, кромка стола, край листа бумаги, место, соединения двух стен комнаты, луч света. При начертании прямых линий на практике применяют линейку.
Прямой линии присущи такие характерные особенности:
1.У прямой линии нет ни начала ни конца, то есть она бесконечна. Существует возможность начертить только ее часть.
2.Через две произвольные точки можно провести прямую линию, и притом только одну.
3. Через произвольную точку можно провести не ограниченное количество прямых на плоскости.
4.Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или они параллельны.
Для обозначения прямой линии используют или одну малую букву латинского алфавита, или две большие буквы, написанные в двух различных местах этой прямой.
Если на прямой линии указать точку, то в результате получим два луча:
Лучом называют часть прямой линии, ограниченную с одной стороны. Для обозначения луча применяют или одну малую букву латинского алфавита, или две большие буквы, из которых одна обозначается в начале луча.
Часть прямой, ограниченная с обеих сторон, именуют ее отрезком. Отрезок, как и прямая линия, обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.
Линию, сформированную несколькими отрезками, не лежащими на одной прямой, принято называть ломаной. Когда концы ломаной совпадают, то такая ломаная именуется замкнутой.
Точка и линия
Я не буду рассказывать вам, что об этом пишут в различных учебниках, ведь вы здесь для того, чтобы понять и применять, а не для того, чтобы зубрить. Я расскажу так, чтобы было понятно.
Точка – это воображаемый геометрический объект, не имеющий никаких размеров и не состоящий ни из чего.
У точки нет ни длины, ни ширины, ни высоты. Ее нельзя измерить. Точка неделимая. Она не состоит ни из каких-либо других частей.
Зачем нужна точка, если она воображаемая? Для чего ее придумали?
Точка выполняет только одну задачу: указание месторасположения.
Пример: точка на карте навигатора указывает нам на то, где находится конечный пункт поездки, то есть, на его местоположение.
Линия – это множество точек, расположенных последовательно друг за другом.
Например, представим себе цепь. Можно вообразить, что каждое ее звено – это точка. И точно так же, как цепь состоит из звеньев, соединенных между собой, так и линия состоит из точек, образно говоря, склеенных друг с другом.
Рис. 1 Цепь и линия
Линия не имеет ширины и высоты, но можно измерить ее длину. Линия состоит из точек.
Как можно измерить то, что состоит из придуманных объектов, не имеющих размеров? Зачем нужна линия?
Действительно, геометрическая точка не имеет размеров, ее невозможно измерить. Но она, как было сказано выше, указывает на местоположение чего-либо конкретного.
Возьмем для примера опять навигатор. Вы на автомобиле проехали от своего дома в любимое кафе.
Рис. 2 Путь автомобиля
Можем ли мы представить автомобиль точкой? Да, можем. Во время движения автомобиль изменял свое местоположение. Чтобы показать на карте, в каких именно местах побывал автомобиль во время поездки, мы обозначим их точками, следовательно, для упрощения рисунка мы смело можем заменить автомобиль точкой. Тогда полный путь от дома к кафе (множество мест на дороге, на которых побывала машина) мы можем изобразить в виде линии, то есть, идущих друг за другом точек. А так как путь от дома к кафе имеет какую-то длину, то и нарисованная линия имеет длину, равную этому пути, а значит, линию можно измерить.
Рис. 3 Контур и диапазон
Как видно на примере рисунка 3-а, при помощи линии обозначено очертание птицы на ветке, а на 3-б – пример решения неравенств методом интервалов.
Для чего нужна линия:
1. Показывает путь движения какого-либо объекта;
2. С ее помощью можно измерить расстояние между какими-нибудь объектами;
3. Служит для обозначения границ объекта или фигуры;
4. Показывает диапазон каких-то значений.
Обозначение точек и линий
Рис. 4 Обозначение точек и линий
Взаимное расположение точек и линии
Точка может принадлежать линии (то есть, быть одной из ее составляющих), а может не принадлежать ей.
Рис. 4.1 Принадлежность точек линии
При записи на письме точка обозначается при помощи знака точка, заключенного в скобки, с добавлением заглавной буквы латинского алфавита: (·) H
Теперь я запишу то, что мы увидели на рисунке 4.1, на языке геометрии, а вы попробуйте прочитать самостоятельно:
Виды линий
Рис. 5 Замкнутая и незамкнутая линия
Замкнутая линия не имеет обрывающихся концов. Она начинается и заканчивается в одной точке. Причем эта точка может находиться в любом месте на этой линии.
Рис. 6 Контур птицы
Незамкнутая линия имеет один или два обрывающихся конца. Начало и конец такой линии находятся в разных местах (точки A и B ).
Рис. 7 Незамкнутые линии
Еще несколько примеров.
1. Ты вышел из дома погулять и вернулся домой. Какой линией можно обозначить твой путь? Правильно, замкнутой.
2. Ты вышел из дома, погулял, а потом зашел к соседу. Какой линией можно обозначить твой путь? Правильно, разомкнутой.
3. Ты вышел из дома и пошел к другу в дом напротив. Какой линией можно обозначить твой путь? Правильно, разомкнутой.
Также линии бывают:
Рис. 11 Самопересекающиеся и не самопересекающиеся линии
Попробуйте сформулировать самостоятельно, какие линии называются самопересекающиеся, а какие – не самопересекающиеся.
Рис. 12 Прямая, ломаная, кривая линии
Более подробно о прямых, кривых и ломаных линиях рассмотрено в других уроках.
Геометрия 7 класс.
Точка, прямая и отрезок
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.
Точка — элементарная фигура, не имеющая частей.
Прямая состоит из множества точек и простирается бесконечно в обе стороны.
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
Как обозначить прямую
Прямую обычно обозначают одной маленькой латинской буквой.
Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.
Задача № 1 из учебника Атанасян 7-9 класс
Решение задачи
Опишем взаимное расположение точек и прямой.
Как обозначается пересечение прямых
Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).
Прямые e и f не имеют общей точки — т.е. они не пересекаются.
Взаимное расположение прямой и точек
Через одну точку (·)A можно провести сколько угодно прямых.
Через две точки (·)A и (·)B можно провести только одну прямую.
Сколько общих точек имеют две прямые
Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых
На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.
Второй случай расположения прямых
Третий случай расположения прямых
Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Задача № 3 из учебника Атанасян 7-9 класс
Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
Решение задачи
Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.
Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или три.
Что такое отрезок
Отрезок — часть прямой, ограниченная двумя точками.
В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.