Что значит проекция в геометрии
Проекция (в геометрии)
В черчении широко применяется частный вид параллельного проектирования, когда плоскость П. расположена перпендикулярно (ортогонально) к направлению проектирования. П. в этом случае называется прямоугольной или ортогональной.
Полезное
Смотреть что такое «Проекция (в геометрии)» в других словарях:
ПРОЕКЦИЯ — (от лат. projectio букв. бросание вперед), изображение пространственных фигур на плоскости (или на какой либо другой поверхности). Центральная проекция: из определенной точки О (центра проекции) через все точки данной фигуры проводятся лучи до… … Большой Энциклопедический словарь
ПРОЕКЦИЯ — ПРОЕКЦИЯ, и, жен. (спец.). 1. Изображение пространственных фигур на плоскости. 2. Передача на экран изображений. | прил. проективный, ая, ое (к 1 знач.) и проекционный, ая, ое (ко 2 знач.). Проективная геометрия (раздел геометрии). Проекционный… … Толковый словарь Ожегова
проекция — и; ж. [от лат. projectio бросание вперёд, вдаль] 1. Матем. Изображение пространственных фигур на плоскости. Картографические проекции. Горизонтальная, вертикальная п. П. пирамиды. Вычертить детали по трём проекциям. 2. Спец. Изображение на экране … Энциклопедический словарь
Проекция (геометрия) — У этого термина существуют и другие значения, см. Проекция. Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая… … Википедия
Проекция — I Проекция (от лат. projectio бросание вперёд, выбрасывание) геометрический термин, связанный с операцией проектирования (проецирования), которую можно определить следующим образом (см. рис. 1): выбирают произвольную точку S пространства… … Большая советская энциклопедия
ПРОЕКЦИЯ — (от лат. projectio, букв. выбрасывание вперёд), изображение пространственных фигур на плоскости (или на к. л. другой поверхности). Центральная П.: из определ. точки О (центра П.) через все точки данной фигуры проводятся лучи до пересечения с… … Естествознание. Энциклопедический словарь
СТЕРЕОГРАФИЧЕСКАЯ ПРОЕКЦИЯ — соответствие между точками сферы и плоскости, получаемое следующим образом; из нек рой точки Sна сфере (центра С. п.) другие точки сферы проектируются лучами на плоскость, перпендикулярную радиусу сферы S0 (на рис. эта плоскость экваториальная,… … Математическая энциклопедия
Начертательная геометрия — раздел геометрии, в котором пространственные фигуры изучаются при помощи построения их изображений на плоскости, в частности построения проекционных изображений, а также методы решения и исследования пространственных задач на плоскости.… … Большая советская энциклопедия
Начертательная геометрия — Начертательная геометрия инженерная дисциплина, представляющая двумерный геометрический аппарат и набор алгоритмов для исследования свойств геометрических объектов. Практически, начертательная геометрия ограничивается исследованием объектов … Википедия
Проекция (геометрия)
Проекция (лат. projectio — выбрасывание вперёд)
Содержание
Общее определение
Отображение 
Проекция из трёхмерного пространства на плоскость
Проекционный метод изображения предметов основан на их зрительном представлении. Если соединить все точки предмета прямыми линиями (проекционными лучами) с постоянной точкой О (центр проекции), в которой предполагается глаз наблюдателя, то на пересечении этих лучей с какой-либо плоскостью получается проекция всех точек предмета. Таким образом получаем на плоскости перспективное изображение предмета или центральную проекцию.
Если центр проекции бесконечно удалён от картинной плоскости, то говорят о параллельной проекции; при этом, если проекционные лучи падают перпендикулярно к плоскости — то об ортогональной проекции, а если наклонно — о косоугольной проекции.
Если плоскость проекции не параллельна ни одной из координатных плоскостей — это аксонометрическая проекция.
Проекция из произвольного пространства на его подпространство
Проекция в этом смысле (упомянутая во введении в пункте 2) — широко применяется в линейной алгебре (подробнее, см.: Проекция (линейная алгебра)), но на практике не только в достаточно абстрактных контекстах, но и при работе с векторами любой природы, размерности и степени абстракции, и даже в элементарной геометрии, а также — очень широко — при использовании прямолинейных координат (как прямоугольных или аффинных).
Отдельно следует упомянуть проекцию точки на прямую и проекцию вектора на прямую (на направление).
Ортогональная проекция на прямую и на направление
Чаще всего используется ортогональная проекция.
Термин проекция в этом смысле употребляется и в отношении самой операция проектирования, и в отношении её результата (при операции проектирования на прямую образы точки, вектора, множества точек называются проекцией точки, вектора, множества точек на эту прямую).
Элементарное описание ортогональной проекции точки на прямую сводится к тому, что из точки на прямую следует опустить перпендикуляр, и его пересечение с прямой даст образ точки (проекцию точки на эту прямую). Это определение работает и на плоскости, и в трёхмерном пространстве, и в пространстве любой размерности.
Элементарное определение проекции вектора на прямую легче всего дать, представив вектор направленным отрезком. Тогда на прямую можно спроектировать его начало и его конец, и направленный отрезок от проекции начала к проекции конца исходного вектора даст его проекцию на прямую.
Проекцией вектора на некоторое направление обычно называют число, совпадающее по абсолютной величине с длиной проекции этого вектора на прямую, определяющую это направление; знак же числа выбирается так, что оно считается положительным, когда направление этой проекции совпадает с данным направлением, и отрицательным, когда направление противоположно.
Неортогональная проекция на прямую и на направление
Неортогональная проекция используется реже, к тому же даже при использовании, особенно в элементарных контекстах, этот термин не всегда используется.
Проще всего неортогональную проекцию на прямую можно задать, задав саму эту прямую и плоскость (в двумерном случае — вместо плоскости другую прямую, в случае n-мерного пространства — гиперплоскость размерности (n-1)), пересекающую прямую. Проекция точки определяется как пересечение плоскости (гиперплоскости), содержащей эту точку и параллельную плоскости, задающей проекцию.
В случае, когда плоскость (гиперплоскость), задающая проекцию, ортогональна прямой, мы получаем ортогональную проекцию (это может быть её альтернативным определением). Поэтому собственно для неортогональной проекции надо потребовать, чтобы эта ортогональность отсутствовала.
Для неортогональной проекции вектора на прямую и на направление определения получаются, исходя из приведённого определения проекции точки, прямо аналогично тому, как это было описано в параграфе об ортогональной проекции.
Тем не менее понятие неортогонального проектирования может быть полезным (по крайней мере, если не бояться терминологической путаницы) для введения косоугольных координат и работы с ними (через них может быть в принципе довольно легко определено понятие координат точки и координат вектора в этом случае).
Значение слова «проекция»
1. Мат. Изображение пространственных фигур на плоскости.
2. Спец. Изображение на экране неподвижных объектов, полученное оптическим способом.
[От лат. projectio — бросание вперед, вдаль]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Проекция (геометрия) — изображение трёхмерной фигуры на так называемой картинной (проекционной) плоскости.
Картографическая проекция — математически определённый способ отображения поверхности эллипсоида на плоскости.
Проекция, проецирование — получение изображения из оптического прибора на удалённом от него экране.
Проекция (реляционная алгебра) — одна из операций над отношениями в реляционных базах данных.
Проекция (теория множеств) — операция, выбирающая одну или несколько компонент их каждого элемента множества кортежей.
Проекция (психология) — механизм психологической защиты индивида.
ПРОЕ’КЦИЯ, и, ж. [латин. projectio — бросание вперед, вдаль]. 1. Геометрическое изображение на плоскости, получаемое при проведении перпендикуляров из всех точек данного тела на эту плоскость (мат.). Параллельные проекции. Прямоугольные проекции. Картографические проекции. 2. Передача на экран рисунков, кино-кадров (спец.). 3. В идеалистической философии — отнесение получаемых человеком ощущений к вызывающим их предметам и явлениям материального мира (филос.).
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
прое́кция
1. геометр. перенос точек фигуры с помощью пучка воображаемых проецирующих световых или зрительных лучей ◆ Географическая карта является изображением участка земной поверхности в той или иной проекции.
2. геометр. изображение, полученное с помощью такого [1] переноса ◆ План здания представляет собой его проекцию на горизонтальную плоскость ◆ Плоский вектор полностью определяется своими проекциями на координатные оси.
3. геометр. величина такого [2] изображения ◆ Координаты точки можно определить как проекции её радиуса-вектора на оси координат.
4. увеличенное изображение на экране неподвижных или подвижных объектов с помощью светооптического устройства
Фразеологизмы и устойчивые сочетания
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: господень — это что-то нейтральное, положительное или отрицательное?
Что значит «проекция (в геометрии)»
Большая Советская Энциклопедия
Проекция (от лат. projectio ≈ бросание вперёд, выбрасывание), геометрический термин, связанный с операцией проектирования (проецирования), которую можно определить следующим образом (см. рис. 1): выбирают произвольную точку S пространства в качестве центра проектирования и плоскость П’, не проходящую через точку S, в качестве плоскости проекций (картинной плоскости). Чтобы спроектировать точку А (прообраз) пространства на плоскость П’, через центр проекций S («глаз») проводят прямую SA до её пересечения в точке А’ с плоскостью П’. Точку А’ (образ) и называется проекцией точки А. Проекцией фигуры F называется совокупность П. всех её точек. Прямая линия, не проходящая через центр П., проектируется в виде прямой. Описанная П. носит название центральной или конической. Она существенно зависит от выбора центра проекций S. При проектировании точек данной плоскости П на плоскость П’ (см. рис. 2) встречаются следующие затруднения. На плоскости П имеются такие точки, для которых не существует образов на плоскости П’. Такова, например, точка В, если проектирующая прямая SB параллельна плоскости П’. Для устранения этого затруднения, происходящего от свойств евклидова пространства, последнее пополняют бесконечно удалёнными элементами (несобственными элементами). Именно, принимают, что параллельные прямые BS и РА’ пересекаются в бесконечно удалённой точке B’; тогда её можно считать образом точки В на плоскости П’. Аналогично бесконечно удалённая точка С является прообразом точки C’ (см. рис. 2). Благодаря введению бесконечно удалённых элементов, между точками плоскости П и точками плоскости П’ устанавливается взаимно однозначное соответствие, осуществляемое при помощи центральной П. Такое соответствие носит название перспективной коллинеации.
Большое практическое значение имеет вид проектирования, при котором центром П. является бесконечно удалённая точка пространства ═(см. рис. 3). При этом все проектирующие прямые параллельны и П. называется параллельной или цилиндрической. Взаимно однозначное соответствие между точками плоскостей П и П’, установленное при помощи параллельного проектирования, называется перспективно-аффинным или родственным (см. Аффинные преобразования ).
В черчении широко применяется частный вид параллельного проектирования, когда плоскость П. расположена перпендикулярно (ортогонально) к направлению проектирования. П. в этом случае называется прямоугольной или ортогональной.
Транслитерация: proektsiya (v geometrii)
Задом наперед читается как: )ииртемоег в( яицкеорп
Проекция (в геометрии) состоит из 20 букв
Метод проекций в начертательной геометрии с примерами
Содержание:
Для обозначения геометрических фигур и их проекций, для отображения отношений между геометрическими фигурами, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем используется геометрический язык, составленный из элементов и символов.
Особое внимание уделяется символам, которые используются для обозначения проекций геометрических фигур.
В предлагаемом издании приняты следующие обозначения:
17. Отображение —
Из истории графических изображений:
Графические изображения появились на ранних ступенях развития человеческого общества. Судя по тем из них, которые дошли до нашего времени, они были тесно связаны с производством и ремеслом. Первые изображения выполнялись простейшими инструментами и в виде рисунков, отражающих только внешнюю форму предметов.
Дальнейшее развитие производственной деятельности человека потребовало более точного изображения пространственных предметов. Строительство крепостных укреплений и различных сооружений требовало их предварительного изображения на плоскости. Сохранившиеся остатки величественных сооружений античного мира говорят о том, что при их строительстве использовались планы и другие изображения возводимых сооружений.
Интенсивно развивалась графика и в Древней Руси, причем развитие шло своим собственным самобытным путем. До нас дошли выполненные по соответствующим правилам план города Пскова (1581), «Чертеж Московского кремля» (1600), «Чертежная книга Сибири», составленная Семеном Ремезовым в 1701 г.
Широкое разнообразие выполняемых чертежей потребовало единых правил и условностей их изготовления. В России они регламентируются Государственными стандартами России, а чертежи, предназначенные для разных стран международными стандартами ISO.
Метод проекций
Изображения объектов трехмерного пространства на плоскости получают методом проецирования.
Аппарат проецирования включает в себя проецируемый объект, проецирующие лучи и плоскость, на которой получается изображение объекта.
Центральное проецирование
Точки 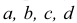
Центральные проекции b и с двух различных точек В и С, лежащих на одной проецирующей прямой, совпадают. Следовательно, при заданных плоскости проекции и центре проецирования одна точка в пространстве имеет одну центральную проекцию. Но одна проекция точки не позволяет однозначно определить положение точки в пространстве. Для обеспечения обратимости чертежа нужны дополнительные условия.
Центральным проецированием может быть построена проекция любой линии или поверхности как множество проекций всех ее точек. При этом проецирующие прямые, проведенные через все точки кривой линии, образуют проецирующую коническую поверхность (рис. 2.2) или могут оказаться в одной плоскости (рис. 2.3).
Проекция кривой линии представляет собой линию пересечения проецирующей конической поверхности с плоскостью проекций. Так на рис. 2.2 проецирующая коническая поверхность Ф пересекается с плоскостью проекций Р по кривой ab, являющейся проекцией линии АВ. Однако проекция линии не определяет проецируемую линию, так как на проецирующей поверхности может быть бесчисленное количество линий, проецирующихся в одну и ту же линию на плоскости проекций.
Свойства центрального проецирования
1. При центральном проецировании:
2. При заданном центре проецирования фигуры на параллельных плоскостях подобны.
3. Центральное проецирование устанавливает однозначное соответствие между фигурой и ее изображением, например изображения на киноэкране, фотопленке. Центральные проекции имеют большую наглядность, но имеют и недостатки. Они заключаются в сложности построения изображения предмета и определения его истинных размеров. Поэтому этот способ имеет ограниченное применение. Его применяют при построении перспектив зданий и сооружений, в живописи и т.д.
Параллельное проецирование
На рис. 2.5 направление проецирования указано стрелкой под углом а^90° к плоскости проекций Р.
При параллельном проецировании сохраняются все свойства центрального проецирования, которые дополняются новыми:
Применяя приемы параллельного проецирования точки и линии, можно строить параллельные проекции поверхности и тела. Параллельные проекции, как и центральные, не обеспечивают обратимости чертежа.
Способы дополнения проекционных чертежей
Прямолинейный отрезок 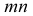
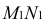
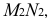
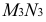
Следовательно, изображение пространственной фигуры является не полным. Мы можем правильно понять чертеж тогда, когда он будет сопровождаться дополнительными пояснениями.
Рассмотрим некоторые способы дополнения проекционного изображения, позволяющие сделать его «обратимым», то есть однозначно определяющим проецируемый предмет.
Способ проекций с числовыми отметками
Этот способ лежит в основе построения чертежей планов местности и некоторых инженерных сооружений (плотин, дорог, дамб и т.п.). Этот способ заключается в том, что положение любой точки в пространстве определяется ее прямоугольной проекцией на некоторую горизонтальную плоскость. Эту плоскость принимают за плоскость нулевого уровня (рис. 2.7).
Рядом с проекциями точек 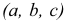
Способ векторных проекций
Способ прямоугольных проекций
Чертеж в системе прямоугольных проекций образуется при проецировании предмета не на одну, а на две или три взаимно перпендикулярные плоскости проекций. Этот способ является частным случаем параллельного проецирования. Направление проецирования 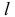
Осуществлять проецирование на две взаимно перпендикулярные плоскости впервые предложил Гаспар Монж.
Чтобы получить проекции точки на плоскости, опускаем из точки А в пространстве перпендикуляры (проецирующие лучи) до встречи с плоскостями Н и V. Проецирующие лучи образуют плоскость Р. Эта плоскость перпендикулярна плоскостям Н и V и пересекает их по прямым, перпендикулярным оси проекций, а саму ось в точке 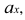
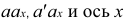
Таким образом, две прямоугольные проекции точки определяют ее положение данной системы взаимно перпендикулярных плоскостей проекций в пространстве относительно
Предметом начертательной геометрии является изложение и обоснование способов построения изображения (проекций) пространственных форм на плоскости и способов решения геометрических задач по заданным изображениям этих форм.
Основными требованиями, предъявляемыми к методам проецирования на плоскость, являются наглядность, точность, обратимость изображений, геометрическая равноценность оригиналу. Изображения, построенные по правилам начертательной геометрии, дают возможность решать с помощью плоских проекций общегеометрические и прикладные задачи.
Наряду с задачей отображения пространственных форм на плоскости чертежа начертательная геометрия дает возможность решать с помощью плоских изображений различные задачи в пространстве. Все задачи начертательной геометрии условно делятся на три основных класса: позиционные, метрические и комплексные.
Позиционными называются задачи на определение общих элементов геометрических фигур. Вопросы принадлежности точки или линии какому-либо геометрическому образу, задачи на пересечение и параллельность геометрических фигур относятся к классу позиционных. В позиционных задачах выясняются вопросы, связанные с взаимным расположением геометрических образов, а вопросы измерений не затрагиваются.
Метрическими называются задачи, в которых требуется определить геометрические величины: расстояния, углы, площади, объемы и т.д. К этому классу относятся задачи на определение длины отрезка прямой и углов его наклона к плоскостям проекции, расстояния между различными геометрическими образами и др.
Комплексные задачи включают в себя как вопросы взаимного расположения геометрических образов, так и вопросы их измерения.
Начертательная геометрия по своему содержанию и методам решения задач занимает особое положение среди других наук. Обогащая точные науки наглядностью и простотой решения многих проблем, начертательная геометрия находит применение в механике, кристаллографии, оптике, то есть всюду, где возникает необходимость в пространственных построениях. Многие задачи, изучаемые в аналитической геометрии, могут быть решены графическими методами начертательной геометрии.
Как и другие точные науки, начертательная геометрия развивает логическое и абстрактное мышление, пространственное воображение.
Рассмотрим метод проекций более подробно:
Принятые обозначения:
Проекции геометрических образов обозначают теми же буквами, какими обозначены их оригиналы, и добавляют подстрочный индекс, соответствующий индексу плоскости проекций:
Наклонная черта (/), перечеркивающая тот или иной символ, означает отрицание данного действия:
Примеры использования символов:
Что такое метод проекций
Евклидово пространство и его реконструкция:
При проецировании решается прямая задача начертательной геометрии, т.е. трехмерные объекты (предметы, оригиналы) изображаются на плоскости, строится чертеж.
Однако принятие аксиомы Евклида о параллельности приводит к трудностям, связанным с неоднородностью евклидова пространства и погруженных в него г.о., когда речь заходит о проецировании.
Действительно, пусть даны две прямые 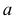
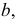
В плоскости 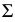
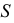
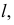
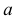
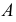
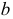
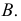
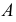
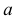
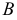
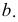

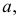
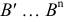
Если проводится 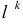
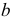
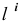
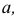
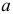
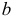
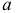
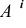
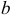
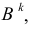
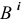
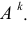
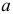
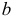
Русский математик Н.И. Лобачевский (1792-1856) предложил считать пространство (плоскость) однородным, подвергнув сомнению существование аксиомы о параллельности. Ученый дополнил плоскость 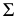
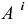
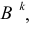
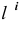
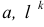
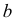
Добиться однородности трехмерного евклидова пространства можно путем добавления к нему несобственных (бесконечно удаленных) элементов.
Евклидовы плоскость и пространство, дополненные бесконечно удаленными точками, прямыми и плоскостями, называются проективными.
Для проективной плоскости справедливы утверждения:
В проективном пространстве:
Создав пространство, в котором без всяких исключений может осуществляться операция проецирования, рассмотрим способы получения центральных и параллельных проекций.
Центральное проецирование
Чтобы спроецировать любую точку пространства на плоскость проекций 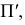
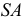
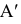
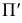
Таким образом, центральной проекцией какой-либо точки пространства называется точка пересечения проецирующего луча, проходящего через центр проекций и данную точку, с плоскостью проекций.
Центральное проецирование называют также коническим, так как проецирующие лучи, проходящие через точки кривой линии 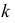
Параллельное проецирование
Параллельное проецирование является частным случаем центрального проецирования, когда центр проекций находится в бесконечно удаленной точке 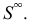
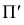
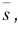
Чтобы спроецировать точку 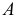
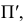
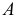
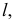
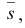
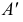
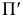
Параллельной проекцией какой-либо точки пространства называется точка пересечения проецирующего луча, параллельного направлению проецирования, с плоскостью проекций.
Множество проецирующих лучей, проходящих через точки кривой линии 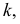
В зависимости от угла наклона проецирующего луча к плоскости проекций параллельные проекции делятся на косоугольные, если угол отличен от прямого (рис. 7), и прямоугольные, если проецирующий луч перпендикулярен плоскости проекции (рис. 8).
Инвариантные свойства проецирования
Геометрические образы проецируются на плоскость проекций в общем случае с искажением. При этом характер искажения проекции по сравнению с оригиналом зависит от аппарата проецирования и положения проецируемого предмета относительно плоскости проекций. В частности, при параллельном проецировании нарушаются метрические характеристики.
Наряду с этим между оригиналом и его проекцией существует определенная связь, заключающаяся в том, что некоторые свойства оригинала сохраняются и на его проекции. Такие свойства принято называть проективными или инвариантными (независимыми) для данного способа проецирования.
Общие свойства центрального и параллельного проецирования
Свойство 1. Проекция точки есть точка.
Это свойство следует из самого способа построения проекции точки.
Свойство 2. Проекция кривой линии есть кривая линия.
Действительно, проецирующие коническая (см. рис. 4) или цилиндрическая (см. рис. 6) поверхности, проходящие через данную кривую, пересекаются с плоскостью проекций по кривой линии.
Свойство 3. Проекция прямой есть прямая (рис. 9).
Проецирующие лучи образуют проецирующие плоскости 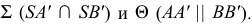
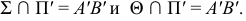
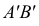
Для построения проекции прямой достаточно построить проекции двух ее точек и соединить их.
Исключение представляет собой прямая 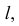
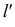
Свойство 4 (это свойство известно как собирательное свойство проекций проецируемых г.о.).
Проекции любых точек 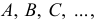
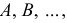
Свойство 5. Если точка принадлежит прямой, то проекция точки принадлежит проекции прямой (рис. 13).
Проецирующий луч 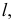
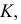
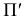
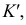
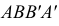
Из свойства 5 вытекают два следующих (6, 7):
Свойство 6. Точка пересечения линий проецируется в точку пересечения проекций этих линий (рис. 14).
Свойство 7. Прямая, касательная к кривой линии, проецируется в касательную к проекции данной кривой (рис. 15).
Свойства параллельного (в том числе ортогонального) проецирования
Свойство 8. Проекции параллельных прямых параллельны (рис. 16). Плоскости 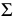
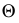
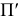
Свойство 9. Отношение отрезков, принадлежащих параллельным прямым или одной прямой, равно отношению проекций этих отрезков.
Доказательство для двух параллельных прямых (см. рис. 16)
Проводятся 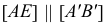

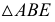
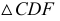
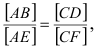
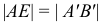
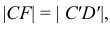
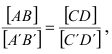
Доказательство для одной прямой (рис. 17).
Известно, что длины отрезков двух прямых 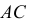
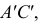
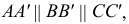
Свойство 10. Любой отрезок прямой, параллельной плоскости проекций, проецируется на эту плоскость без искажения (рис. 18).
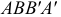
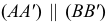
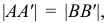
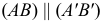
Свойство 11. При параллельном переносе плоскости проекций величина проекций не меняется (рис. 19).
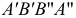
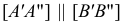
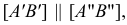
Свойcтва ортогонального проецирования
Из чертежа модели (см. рис. 20) видно, что длину отрезка прямой 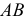
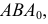
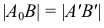
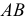
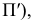
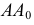
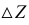
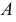
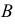
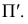
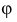
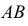
Свойство 13. Любая плоская фигура, параллельная плоскости проекций, проецируется на эту плоскость без искажения (рис. 21).
Если треугольник 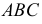
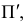
Свойство 14. Проекция любого г.о. не может быть больше самой фигуры. Это свойство вытекает из свойств 10, 12, 13.
Свойство 15 (известно как теорема о проецировании прямого угла).
Если одна сторона прямого угла параллельна плоскости проекций, а другая ей не перпендикулярна, то на эту плоскость проекций прямой угол проецируется без искажения (рис. 22).
Дано: 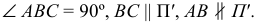
Доказательство: прямая 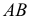
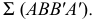
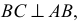
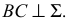
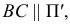

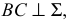
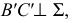
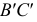
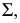
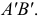
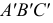
Обратимость проекционных чертежей
По одной проекции окружности нельзя определить, какой г.о. спроецирован на 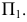
В зависимости от способа дополнения однопроекционного чертежа существуют следующие методы:
В методе Монжа дополнением однопроекционного чертежа является проекция на вторую плоскость (рис. 24, 25). Более подробно этот метод изложен в разделе II.
В проекциях с числовыми отметками одну ортогональную проекцию точки дополняет числовая отметка, указывающая расстояние от точки до плоскости проекций (рис. 26).
На чертеже обязательно приводится линейный масштаб, который вместе с числовой отметкой позволяет сделать чертеж обратимым.
Проекции с числовыми отметками применяются в инженерно-строительном деле или при изображении объектов, у которых высота невелика по сравнению с длиной и шириной.
Обратимость аксонометрических проекций (рис. 27) и перспективных проекций (рис. 28) достигается благодаря так называемым вторичным проекциям 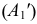
Всё о методе проекций
Будущий инженер-судостроитель, работающий в конструкторском бюро, на судостроительном заводе или занимающийся проектированием судовых обводов, должен уметь отчетливо представлять себе в пространстве образ будущего судна, свободно ориентироваться в геометрии его отдельных частей. На практике такое умение означает способность выполнять чертежи судовых обводов в ортогональных и аксонометрических проекциях. В основе построения обоих типов проекций лежит операция проецирования.
Операция проецирования
Выберем в пространстве некоторую произвольно расположенную плоскость 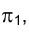
Прямая, проходящая через точки S и А, называется проецирующим лучом, а точка ее пересечения с плоскостью 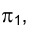
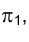
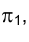
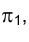
Если угол, образованный направлением проецирующих лучей с плоскостью проекций 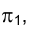
Несобственные элементы пространства
Операция проецирования как способ образования геометрических моделей опирается на представление о геометрическом пространстве и его элементах. Элементами трехмерного геометрического пространства являются точки, прямые и плоскости, находящиеся в определенных соотношениях.
Имеется, однако, два случая, в которых данный изоморфизм нарушается. Укажем на прямой n точку М, лежащую на луче SМ.
Проецирующий луч SМ параллелен прямой 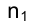
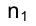
Из вышесказанного следует, что точечное соответствие, установленное между прямыми 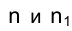
Для того, чтобы определить соответствующие элементы пространства и замкнуть операцию проецирования, достаточно потребовать, чтобы две параллельные прямые считались пересекающимися, причем точку их пересечения назовем несобственной точкой.
Приведенные рассуждения о точке пересечения двух параллельных прямых справедливы для любых двух параллельных прямых пространства. Следовательно, каждая прямая пространства имеет единственную ей принадлежащую несобственную точку, называемую также бесконечно удаленной. Естественность такого определения легко прослеживается из рис. 1.4.
Выясним, что представляет собой геометрическое место несобственных точек, лежащих в произвольной плоскости. Поскольку каждая прямая такой плоскости имеет единственную несобственную точку, то она должна пересекать упомянутое геометрическое место лишь в одной точке. Геометрическим местом несобственных точек плоскости естественно поэтому считать прямую линию. Итак, на каждой плоскости имеем несобственную или бесконечно удаленную прямую.
Рассмотрим две параллельные плоскости 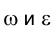
Две прямые 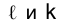
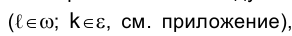
Определим теперь геометрическое место несобственных точек пространства. Дополнив каждую прямую несобственной точкой, а каждую
плоскость несобственной прямой, получим множество несобственных элементов пространства. Рассматривая это множество как некоторое геометрическое место точек, заметим, что оно имеет с каждой прямой одну общую точку и с каждой плоскостью одну общую прямую. Естественно поэтому рассматривать его как несобственную или бесконечно удаленную плоскость.
Введение бесконечно удаленных элементов пространства позволяет получить такую геометрическую модель физического мира, в котором операция проецирования осуществляется без всяких исключений. Пространство, полученное присоединением к евклидову пространству этих элементов, называется поэтому проективным пространством.
Приведем ряд утверждений, справедливых в проективном пространстве:
Метод двух изображений
Вернемся к рис. 1.1. Попытаемся по проекции точки 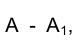
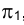
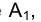
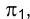
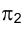
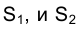
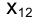
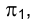
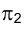
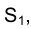
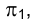
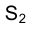
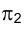
Совокупность точек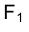
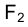
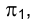
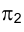
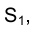
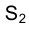
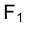
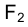
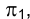
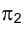
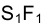
Из сказанного следует, что, зная положение исключенных точек 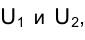
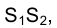
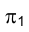
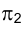
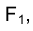
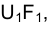
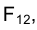
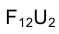
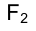
Рассмотренный метод построения геометрической модели объекта называется методом двух изображений.
Недостатком построенной выше модели точки является наличие двух, связанных с пространством, произвольно ориентированных друг относительно друга плоскостей проекций, а также произвольность направления проецирующих лучей.
Ортогональное проецирование. Эпюр Монжа
Частным случаем метода двух изображений является широко используемый на практике метод прямоугольного (ортогонального) проецирования точек исследуемого геометрического объекта на две взаимно перпендикулярные плоскости проекций 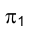
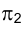
Плоскость 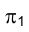
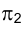
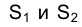
точки. Несобственными в этом случае являются также прямая 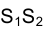
На рис. 1.7 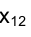
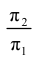
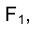
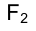
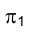
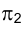
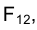
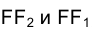
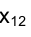
Таким образом, пересечение перпендикуляров, восставленных в точках 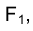
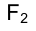
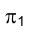
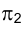
Ясно, конечно, что пространственная конфигурация, состоящая из двух взаимно перпендикулярных плоскостей проекций, на которых строятся ортогональные проекции точек рассматриваемого объекта, громоздка и неудобна в качестве носителя информации о его геометрической форме. Поэтому информацию о геометрических характеристиках изучаемого объекта целесообразно получить на плоскости, т.е. на листе бумаги, кальки и т.д. Как же перейти от системы двух плоскостей проекций к одной?
Рассмотрим рис. 1.7. Повернем плоскость 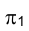
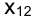
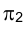
Из этого рисунка видно, что ортогональные проекции на плоскости проекций 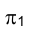
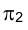
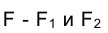
Проецирующие точку F перпендикуляры 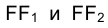
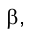
При переходе к эпюру Монжа перпендикулярность прямых 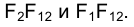
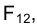
продолжают друг друга.
Таким образом, ортогональные проекции точки на две взаимно перпендикулярные плоскости проекций 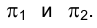
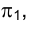
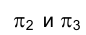
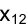
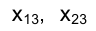
Расстояние точки А от плоскости 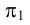
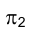
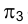
В зависимости от того, положительны или отрицательны численные значения задающих точку в пространстве координат, она располагается в том или ином квадранте и, наоборот, расположение точки в соответствующем квадранте определяет знаки ее координат.
Так, если координаты Y и Z точки, называемые ординатой и аппликатой, положительны, то точка расположена в I квадранте, если Y и Z отрицательны, то точка расположена в III квадранте (рис. 1.12).
В указанном случае на эпюре Монжа ортогональные проекции точек располагаются по разные стороны от оси проекций (рис. 1.13).
Если одна из координат точки Y или Z отрицательна (при положительной абсциссе X), то точка расположена либо во II, либо в IV квадранте, а на эпюре Монжа ее ортогональные проекции располагаются по одну сторону оси проекции: либо вверх, либо вниз (рис. 1.14, 1.15).
На практике система ортогональных плоскостей проекций может располагаться по разному относительно исследуемого геометрического объекта.
На рис. 1.16 плоскости проекций 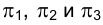
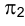
продольной симметрии, плоскость 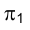
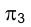
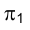
Для того, чтобы яснее представить себе положение точки исследуемого объекта, удобно воспользоваться вспомогательным изображением, которое получается на плоскости проекций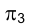
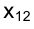
Введем в рассмотрение плоскости, делящие пополам координатные углы, образованные плоскостями проекций 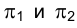
Так, плоскость, делящая пополам I и III квадранты, называется плоскостью симметрии или нечетной биссекторной плоскостью и обозначается 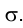
Координаты X и Y точки, принадлежащей плоскости симметрии, одинаковы по величине и знаку, а на эпюре Монжа ее проекции располагаются симметрично относительно оси 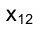
Ортогональные проекции прямой линии, двух прямых
В архитектурном облике современного судна отрезки прямых линий встречаются достаточно часто. Они формируют в основном контуры вырезов люков (рис. 1.21) на сухогрузных судах: контуры мачт, грузовых стрел и т.д. Поэтому умение правильно изобразить моделируемый отрезком прямой элемент соответствующей реальной конструкции очень важно для инженера-судостроителя.
Пусть в пространстве отрезок прямой АВ моделирует часть грузовой стрелы сухогруза, и нам следует определить изображение этой стрелы на горизонтальной и вертикальной плоскостях, т.е. плоскостях проекций 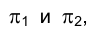
Для того чтобы построить ортогональные проекции отрезка АВ на плоскости 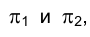
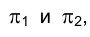
Положение любой прямой в пространстве определяется, как известно, двумя принадлежащими ей точками (например А и В, рис. 1.23), поэтому для построения ортогональных проекций произвольной прямой линии на плоскостях проекций 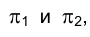
Известно, что две параллельные между собой прямые определяют плоскость. На рис. 1.24 греческими буквами 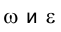
Плоскость 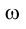
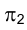
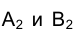
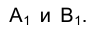
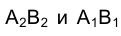
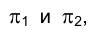
Выберем на отрезке прямой AВ точку С, расположенную между А и В (см. рис. 1.24). Основания проецирующих точку С на плоскости 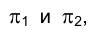
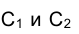
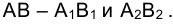
Таким образом, если эпюре Монжа на заданы проекции отрезка прямой линии 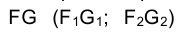
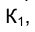
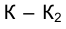
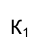
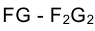
Проанализируем теперь вопрос о том, как влияет положение оси проекций 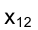
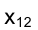
При этом на эпюре Монжа проекции отрезка прямой 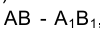
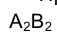
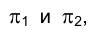
Изменились лишь координаты принадлежащих отрезку точек: их ординаты уменьшились, а аппликаты увеличились на одну и ту же величину К. Это эквивалентно перемещению фронтальной плоскости проекций 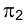
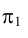
На рис. 1.28 иллюстрируется рассмотренное выше перемещение плоскостей проекций 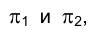
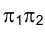
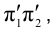
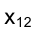
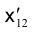
На рис. 1.29 приведены проекции точки F отрезка АВ, принадлежащей плоскости тождества. Видно, что ее положение единственно и не зависит от положения оси проекций. Приведенные соображения убедительно свидетельствуют о том, что изображения геометрического объекта не зависят от положения оси проекций на эпюре Монжа, от ее наличия или отсутствия на нем. При изображении технических объектов ось проекций не используется вообще, а определяя направление линии связи, говорят, что оно всегда перпендикулярно направлению оси проекций.
Приведенные на рис. 1.22, 1.24 варианты расположения отрезка прямой относительно плоскостей проекций характеризуют так называемую прямую общего положения, т.е. прямую, произвольным образом наклоненную к обеим плоскостям проекций.
Рассмотрим решение задачи об определении длины отрезка прямой линии (иногда вместо слова «длина» употребляют термин «истинная величина» отрезка прямой, подчеркивая, что на плоскостях проекций отрезки прямых в общем случае изображаются в искаженном виде). Практической иллюстрацией к этой задаче может служить рис. 1.30, на котором приведен фрагмент грузовой стрелы сухогруза, контуры люка в пространстве и в ортогональных проекциях. Определение истинной величины отрезка FG позволит графически найти длину грузовой стрелы судна.
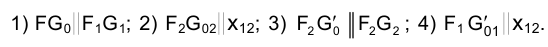
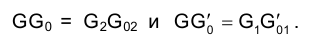
Уяснение смысла записанных равенств очень важно.
Отрезок 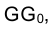
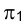
Отрезок 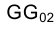
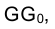
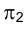
Аналогично отрезок 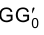
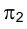
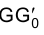
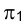
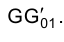
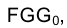
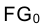
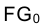
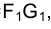
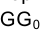
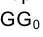
Для того чтобы определить длину отрезка FG на эпюре Монжа, следует восставить, например, в точке G1 перпендикуляр к горизонтальной проекции отрезка 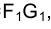
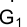
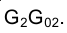
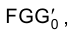
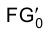
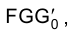
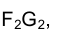
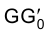
Для определения длины отрезка FG на эпюре Монжа теперь следует восставить перпендикуляр в точке 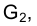
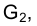
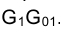
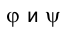
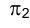
При решении различных типов практических задач часто приходится рассматривать ситуации, в которых геометрические конфигурации моделируются отрезками прямых, занимающих некоторое характерное частное положение относительно плоскостей проекций 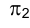
Прямые, параллельные плоскостям проекций
На рис. 1.32 приведено изображение прямой линии, параллельной горизонтальной плоскости проекций 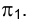
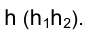
На эпюре Монжа изображение горизонтали характеризуется тем, что ее фронтальная проекция 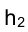
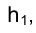
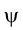
Длина горизонтали h в пространстве определяется длиной ее горизонтальной проекции 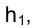
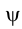
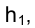
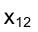
Прямая, параллельная фронтальной плоскости проекций 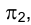
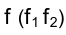
На эпюре Монжа горизонтальная проекция фронтали 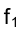
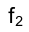
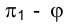
Монжа определяется углом между ее фронтальной проекцией 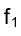
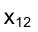
Из приведенных выше рассуждений становится очевидным изображение на эпюре Монжа прямой, параллельной оси проекций, g (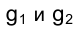
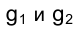
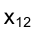
Прямые, перпендикулярные плоскостям проекций
Прямые, перпендикулярные плоскостям проекций, называют проецирующими (рис.1.37). Если прямая ℓ перпендикулярна горизонтальной плоскости проекций 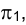
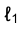
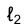
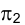
У прямой n, перпендикулярной фронтальной плоскости проекций 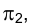
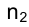
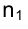
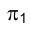
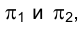
в профильной плоскости проекций 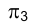
На эпюре Монжа обе проекции любой профильной прямой m совпадают с направлением линии связи (рис. 1.40).
Анализ рассмотренных частных положений прямой позволяет сформулировать вывод о том, что прямая, параллельная плоскости проекций, проецируется на эту плоскость проекций без искажения.
В соответствии с взаимной ориентацией в пространстве прямые линии могут быть: а) параллельными; б) пересекающимися; в) скрещивающимися. Наиболее характерным практическим применением перечисленных типов взаимного расположения прямых могут служить автомобильные дороги, линии электропередач высокого напряжения и т.д.
Пересекающиеся прямые
Для пересекающихся в пространстве прямых линий характерно наличие общей точки (рис. 1.43). Линия пересечения плоскостей, проходящих через перпендикуляры, проецирующие точки отрезков пересекающихся прямых FG и СD на какую-либо плоскость проекций, например 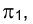
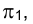
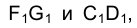
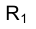
Из сказанного следует, что на эпюре Монжа точки 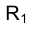
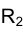
Если отрезки пересекающихся прямых располагаются в плоскости, перпендикулярной какой-либо плоскости проекций, например p1, то на эпюре
Монжа их горизонтальные проекции совпадают (см.рис. 1.44).
Случай пересечения профильных прямых не является столь очевидным, как случай пересечения прямых общего положения.
Поэтому определение проекций точки пересечения двух профильных прямых на эпюре Монжа требует проведения дополнительных построений, основанных на косоугольном параллельном проецировании обеих пересекающихся профильных прямых на плоскость тождества (рис. 1.45).
На эпюре Монжа (рис. 1.46) вспомогательные прямые 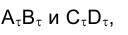
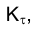
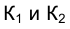
Параллельные прямые
Плоскости 
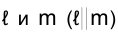
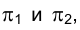
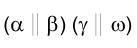
Следовательно, и линии пересечения этих плоскостей с плоскостями 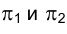
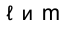
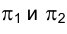
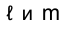
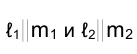
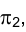
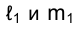
Прямые, принадлежащие профильной плоскости проекций, называются профильными (рис. 1.50). Независимо от взаимной ориентации профильных прямых в пространстве их проекции всегда параллельны, так как они перпендикулярны направлению оси проекций
Поэтому для выяснения вопроса о том, параллельны ли в пространстве профильные прямые, проекции которых заданы на эпюре Монжа, необходимо провести некоторые вспомогательные построения. Метод вспомогательных прямых, иллюстрируемый рис. 1.50, основан на параллельном косоугольном проецировании обеих параллельных прямых на плоскость тождества.
Рис. 1.50 иллюстрирует решение задачи о построении проекций отрезка СD, параллельного отрезку АВ на эпюре Монжа, если заданы его фронтальная проекция 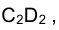
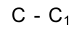
Скрещивающиеся прямые
Примерами скрещивающихся прямых могут служить случаи идущие на разных уровнях автострады, всевозможные транспортные развязки, проложенные на разных уровнях судовые системы и т.д.
На эпюре Монжа одноименные проекции скрещивающихся прямых могут пересекаться, но точки их пересечения не лежат на одной линии связи (рис. 1.51).
Задание плоскости на эпюре Монжа
Плоскость определяется тремя точками, не лежащими на одной прямой. На рис. 1.52 и 1.53 приведены примеры задания плоскости тремя точками в пространстве и на эпюре Монжа.
К другим возможным способам задания плоскости, являющимся следствием указанного выше, следует отнести задание плоскости прямой линией и точкой вне ее (рис. 1.54,а), пересекающимися прямыми (рис. 1.54,б) и параллельными прямыми (рис. 1.54,в).
Плоскости, образующие произвольные углы с плоскостями проекций 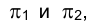
Если плоскость перпендикулярна какой-либо плоскости проекций, она называется проецирующей. Плоскость, перпендикулярная горизонтальной плоскости проекций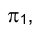
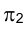
Рассматривая, например, на судне пространственное расположение продольных и поперечных переборок, делящих судно на отсеки,
легко представить себе, что они расположены в горизонтально проецирующих плоскостях.
Проецирующая плоскость обладает тем свойством, что одна из проекций любого лежащего в ней геометрического образа совпадает с линией пересечения этой плоскости с соответствующей плоскостью проекций (рис. 1.57).
На эпюре Монжа проецирующая плоскость, как правило, задается линией ее пересечения с соответствующей плоскостью проекций, называемой следом данной проецирующей плоскости. След проецирующей плоскости на плоскости проекций обозначается какой-либо греческой буквой, используемой для названия плоскости и подстрочного индекса, которым является обозначение плоскости проекций. Например, 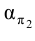
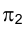
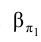
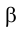
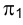
Для решения самых различных задач, связанных с определением тех или иных геометрических элементов плоскости, приходится использовать прямые, лежащие в плоскости и параллельные плоскостям проекций 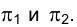
плоскости или прямыми уровня.
Так, прямая, принадлежащая заданной плоскости и параллельная горизонтальной плоскости проекций 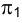
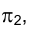
Для того чтобы более наглядно оценить ориентацию главных линий плоскости в пространстве, их можно представить как линии пересечения этой плоскости с плоскостями, соответственно параллельными плоскостям проекций 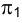
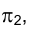
Заметим, что каждой плоскости принадлежит бесчисленное множество фронталей и горизонталей, однако через произвольную точку
плоскости можно провести лишь одну фронталь и одну горизонталь.
Рассмотрим примеры построения главных линий плоскости на эпюре Монжа. Пусть плоскость задана проекциями треугольника 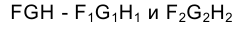
Итак, построим проекции горизонтали 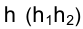
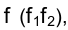
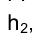
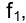
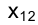
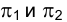
Обозначим через 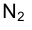
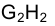
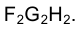
На рис. 1.60 приведены примеры построения горизонталей и фронталей проецирующих плоскостей, различным образом ориентированных относительно плоскостей проекций.
Заметим, что понятие следа плоскости на плоскости проекций характерно не только для проецирующих плоскостей. Под следом в общем случае понимается линия пересечения любой плоскости, в том числе и плоскости общего положения с другой интересующей нас плоскостью.
Выше (см. раздел 1.3) было показано, что при переносе оси проекций плоскость тождества не изменяет своего положения в пространстве. Эта неизменность ее положения относительно рассматриваемых геометрических образов позволяет включать в состав элементов, задающих произвольную плоскость, линию пересечения последней с плоскостью тождества.
Позиционные задачи
Характерной особенностью позиционных задач является то, что в процессе их решения не учитываются метрические свойства фигур те их свойства, которые могут быть выявлены лишь в результате измерения.
В настоящем параграфе рассматриваются основные позиционные задачи, иллюстрирующие решение значительного большинства задач этого класса.
Задача 1.
Построить прямую К, лежащую в данной плоскости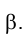
Итак, прямая лежит в плоскости, если она имеет с ней две общие точки (рис. 1.62) или одну общую точку и параллельна некоторой другой прямой, лежащей в той же плоскости (рис. 1.63).
Задача 2.
Построить точку L, лежащую в заданной плоскости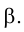
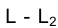
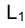
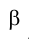
Построение точек, лежащих в проецирующих плоскостях, иллюстрируется рис. 1.65. Так, в частности, точка 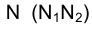
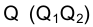
Прежде чем перейти к рассмотрению более сложных позиционных задач, остановимся на некоторых моментах, важных с точки
зрения задания на эпюре Монжа плоских фигур.
В разделе 1.4 были приведены общие способы задания плоскости на эпюре, которые позволили перейти к определению плоскости простейшими геометрическими фигурами, такими как треугольник или четырехугольник: параллельными сторонами.
Если же речь идет о задании плоскости многоугольником с произвольно расположенными сторонами, число которых больше трех, то для получения на эпюре Монжа проекций действительно плоской в пространстве фигуры следует выполнить дополнительные построения, убеждающие в принадлежности всех вершин многоугольника одной плоскости. На рис. 1.66 задана фронтальная проекция пятиугольника 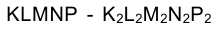
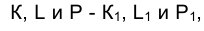
Требуется достроить горизонтальную проекцию пятиугольника в предположении, что он является плоской фигурой.
Рассмотренный пример убеждает в том, что любая плоская фигура может быть использована для задания плоскости; если же фигура ограничена кривыми линиями, то на эпюре Монжа она может быть построена с помощью вспомогательных прямых, лежащих в ее плоскости и пересекающих заданные кривые.
Задание плоскости плоской фигурой иначе называется заданием плоскости отсеком, под которым понимается часть плоскости, ограниченная некоторым контуром.
Задача 3.
Определить точку F пересечения прямой ℓ и горизонтально проецирующей плоскости 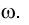
Так, на рис. 1.67 показаны проекции отрезка АВ прямой, лежащей в горизонтально проецирующей плоскости 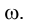
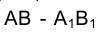
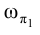
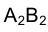
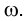
Отмеченное обстоятельство позволит нам строить через прямые проецирующие их плоскости.
Рис. 1.68 иллюстрирует расположение отрезка СD некоторой прямой, расположенной параллельно фронтально проецирующей плоскости 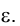
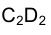
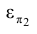
Рассмотренные примеры позволяют теперь уяснить условие и ход решения задачи 3. На рис. 1.69 приведена пространственная интерпретация ее условия и найденного решения, позволяющая сформулировать правило определения проекций точки пересечения произвольной прямой с проецирующей плоскостью на эпюре Монжа (рис. 1.70).
Горизонтальная проекция 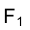
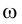
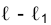
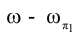
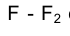
Сформулированное положение справедливо и для случая фронтально проецирующей плоскости (рис. 1.71). В этом случае фронтальная проекция точки пересечения прямой ℓ, с плоскостью 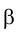
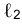
следом плоскости 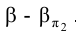
Задача 4.
Определить точку пересечения прямой К общего положения ℓ, с произвольной плоскостью
Составим, прежде всего, алгоритм решения поставленной задачи, рассматривая пространственную картинку (рис. 1.74), соответствующую условиям задачи.
Реализуем установленный алгоритм на эпюре Монжа. Найдем проекции точки 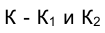
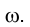
Определим проекции точек пересечения сторон треугольника GH и FН с горизонтально проецирующей плоскостью a. Горизонтальная проекция стороны 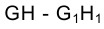
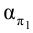
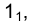
принадлежит фронтальной проекции 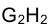
3. Отрезок 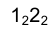

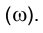
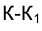
Алгоритм решения задачи 4 описывает, по сути дела, исследование вопроса о взаимном положении произвольных прямой ℓ и плоскости 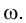
Задача 5.
Определить линию пересечения двух плоскостей 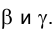
1. Определить линию ℓ пересечения проецирующих плоскостей 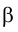
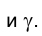
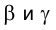
Ее горизонтальная проекция 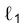
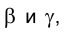
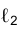
произвольной длины.
Если проецирующие плоскости являются плоскостями разных наименований, например, 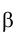
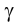
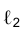
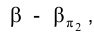
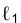
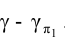
2. Определить линию ℓ пересечения проецирующей плоскости 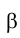
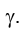
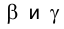
Действительно, плоскость общего положения 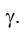
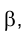
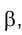
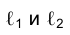
3. Определить линию ℓ пересечения плоскостей общего положения
Составим аналогично задаче 4 алгоритм нахождения решения и рассмотрим пространственную иллюстрацию условия (рис. 1.81).
Таким образом принципиально прямая ℓ, определена в пространстве, поскольку определено положение двух принадлежащих ей точек F и G.
Перейдем теперь к решению задачи на эпюре Монжа. Зададим плоскость 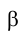
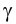
В соответствии с приведенными выше рассуждениями для нахождения точек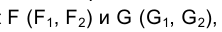
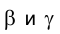
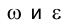
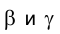
Итак, линия пересечения m плоскости w с заданной плоскостью 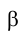
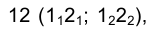
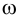
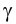
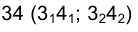
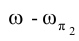
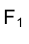
Фронтальная проекция точки 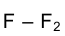
При решении позиционных задач весьма важно сделать чертеж по возможности более наглядным или, как иначе говорят, указать видимость геометрических элементов.
Будем считать, что направление лучей зрения совпадает с направлением проецирующих лучей, т.е. перпендикулярно плоскостям проекций 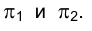
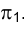
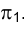
Возвращаясь к задаче 4 (см. рис. 1.75), покажем невидимую часть прямой ℓ, пересекающей плоскость треугольника FGH. Для определения
видимости прямой ℓ на горизонтальной плоскости проекций p1 рассмотрим точки: М, принадлежащую прямой ℓ 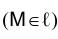
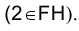
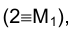
Иногда точки, аналогичные точкам 2 и М, называют конкурирующими. Считая, как было предложено выше, что направление луча зрения совпадает с направлением проецирования на плоскость 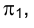
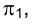
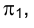
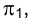
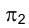
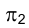
Метрические задачи
Исследуем сначала вопрос о том, какой угол является ортогональной проекцией прямого угла. Напомним, что при ортогональном проецировании плоскости, проецирующие расположение в пространстве стороны прямого угла на плоскости проекций 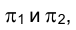
к ним перпендикулярны, и поэтому угол между ними будет равен углу между проекциями лежащих в них сторон угла (рис. 1.84).
Если стороны прямого угла произвольно ориентированы относительно плоскости проекций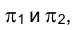
Спроецируем на плоскость 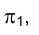
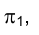
Пусть прямая KM в точке 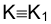
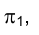
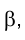

через отрезок МN, в том числе и к горизонтально проецирующей плоскости
Таким образом, двугранный угол, образованный плоскостями 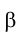
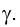
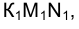
На рис. 1.88 приведены различные варианты проекций прямого угла в тех случаях, когда он проецируется на плоскость без искажения.
Полученные выводы можно распространить и на скрещивающиеся прямые, учитывая, что углом между ними (например, прямыми m
и n, рис. 1.89) называется угол, измеренный между прямыми, проведенными из произвольной точки пространства соответственно параллельно двум данным скрещивающимся прямым.
Таким образом, условия перпендикулярности прямой к плоскости можно сформулировать так: если в пространстве прямая линия ℓ
перпендикулярна некоторой плоскости a, то на эпюре Монжа горизонтальная проекция этой прямой 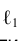
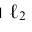
a.
Задача 1.
Из точки К опустить перпендикуляр на плоскость, определяем треугольником LМN, и определить точку встречи его с этой
(рис. 1.91).
Сначала находится горизонтальная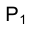
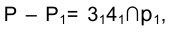
Располагая теперь фронтальной 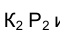
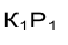
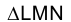
Задача 2.
Для отыскания решения целесообразно провести в пространстве через точку К плоскость 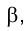
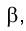
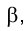
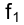
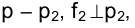
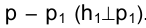
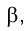
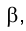
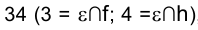
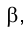
Сначала находится фронтальная 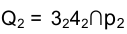
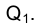
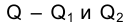
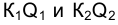
Начертательная геометрия и метод проецирования
Начертательная геометрия по праву считается одной из основных общепрофессиональных дисциплин, изучаемых в высшей школе по многим инженерным специальностям.
Предметом начертательной геометрии является теоретическое обоснование и изложение методов построения пространственных форм на плоскости и способов решения задач геометрического характера по заданным изображениям этих форм.
Правила построения изображений основаны на методе проекций. Поэтому проекционный метод построения изображений является основным методом начертательной геометрии.
Изучение курса начертательной геометрии всегда связано с определенными трудностями, обусловленными своеобразием предмета, сложностью геометрических преобразований, а также отсутствием у многих учащихся опыта пространственного представления и воображения. Последнее обстоятельство предопределяет оторванность проекционного чертежа от реального пространства и геометрического объекта в этом пространстве, что затрудняет восприятие предмета. Поэтому изучение начертательной геометрии ставит целью:
В настоящем учебном пособии в упрощенной форме представлен курс начертательной геометрии для самостоятельного изучения на основе использования большого количества пространственных чертежей, исключения из курса малоприменяемых в производстве тем и подкрепления теоретического материала различными примерами и задачами.
Настоящее учебное пособие предназначено для студентов дневной, вечерней и заочной формы обучения. Оно может быть также полезно для аспирантов и преподавателей графических дисциплин.
Ортогональное проецирование точки
Для отображения геометрической фигуры на чертеже применяют операцию проецирования. Она заключается в том, что через точку пространства проводят проецирующую прямую до пересечения с плоскостью проекций. Точку пересечения проецирующей прямой с плоскостью проекций называют проекцией данной точки на данную плоскость проекций.
Различают следующие методы проецирования:
Чертежи, построенные по методу проецирования, называются проекционными.
Центральное проецирование
Следствием второго свойства является то, что по одной проекции точки невозможно однозначно указать положение точки в пространстве. Для этого требуется иметь две проекции точки, полученные двумя
проецирующими прямыми, проведенными из разных центров проекций (рисунок 1.16).
Параллельное проецирование
Параллельное проецирование осуществляется не из центра проекций, а параллельно направлению проецирования S (рисунок 1.2). В этом случае проекции точек называют параллельными проекциями.
Параллельное проецирование подразделяется на косоугольное (угол между проецирующей прямой и плоскостью проекций не равен 90 градусов) и прямоугольное или ортогональное (угол равен 90 градусов). Свойства параллельного проецирования аналогичны свойствам центрального проецирования.
Ортогональное проецирование на одну плоскость проекций
Ортогональное проецирование является частным случаем параллельного проецирования. Оно заключается в проведении проецирующей прямой через объект перпендикулярно плоскости проекций
Н (рисунок 1.26). Кроме вышеуказанных свойств центрального проецирования можно привести дополнительно следующие свойства ортогонального проецирования:
Ортогональное проецирование на две плоскости проекций
ОХ влево, оси 0Y к наблюдателю, оси 0Z вверх приняты за положительные. Обратные направления приняты за отрицательные.
Две проекции точки однозначно определяют положение точки в пространстве.
Преобразуем пространственный макет, представленный на рисунке 1.3а) в плоскостной. Для этого удалим саму точку, оставим лишь её проекции и линии связи. Плоскость проекций Н повернем вокруг оси ОХ так, как показано на рисунке 1.3а), до совмещения с плоскостью V (рисунок 1.36). Далее удалим плоскости проекций и будем их только подразумевать. В результате преобразований получится плоскостной чертеж (рисунок 1.3в), который называют комплексным чертежом точки или эпюром Монжа. На эпюре указаны координаты точки, по которым можно определить положение точки в пространстве.
Ортогональное проецирование на три плоскости проекций
В некоторых случаях требуется проецирование на три плоскости проекций, если, например, геометрический объект имеет сложную конструкцию.
Если все три плоскости проекций продолжить в геометрическом пространстве во все стороны, то оно разделится тремя плоскостями на восемь частей, называемых октантами (рисунок 1.5). Октанты характеризуются различными знаками координат по осям OX, 0Y и 0Z. Знаки координат точки в различных октантах представлены в таблице.
На рисунке 1.6 представлена трансформация пространственной модели первого октанта вместе с проекциями точки в эпюр:
Эпюр точки в трех проекциях положен в основу начертательной геометрии и технического черчения.
Рассмотрим свойства эпюра Монжа, которые вытекают из пространственного чертежа ортогонального проецирования на три плоскости проекций и эпюра:
На рисунке 1.8 представлена связь эпюра Монжа с проекционным черчением и методом проецирования, принятым в курсе технического черчения в соответствие с Единой системой конструкторской документации (ЕСКД).
Пример 1.1.
Построить горизонтальную проекцию точки А. Определить № октанта, в котором расположена точка (рисунок 1.9а).
Решение: На рисунке 1.9в представлен пространственный макет задачи (его полезно делать при решении любой задачи). Решение задачи на эпюре показано на рисунке 1.96.
1) Так как проекции 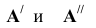
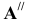
2) Так как точка 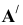
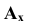
Образование чертежа по Г. Монжу
Проекции точки
Метод проекций предполагает наличие плоскости проекций, объекта проецирования и проецирующих лучей. Проекции могут быть центральными и параллельными. Если все проецирующие лучи проходят через одну точку, называемую центром проекций S, то проекции называются центральными. Если проецирующие лучи параллельны между собой, то проекции называются параллельными.
На рис. 1.1, а показано построение центральных проекций точек A и B (объекты проецирования) на некоторую плоскость проекций H. Проецирующие лучи, проведенные через центр проекций точку S и заданные точки A и B, пересекаются с плоскостью проекций H и определяют центральные проекции А’ и В’ точек A и B.
На рис. 1.1, б показано построение параллельных проекций точек А и В (объекты проецирования) по заданному направлению проецирующих лучей S на некоторую плоскость проекций H. В результате проецирования на плоскости проекций α построены параллельные проекции А’ и В’ взятых в пространстве точек А и В.
Запомните! Проекцией точки называется точка пересечения проецирующего луча с плоскостью проекций.
Соединив прямой линией взятые точки А и В мы получим отрезок АВ, а соединив прямой линией построенные проекции точек мы получим центральную (рис. 1.1, а) и параллельную (рис. 1.1, б) проекции отрезка АВ на плоскости проекций H.
Параллельные проекции могут быть прямоугольными (ортогональными) или косоугольными:
Отметим некоторые свойства параллельного проецирования:
Точка в системе плоскостей проекций H, V и W. Проекции точки в системе прямоугольных координат x, y, z.
Для получения изображений предметов на чертежах французский геометр Гаспар Монж предложил следующий метод – метод параллельного прямоугольного проецирования на взаимно перпендикулярные плоскости проекций.
На рис. 1.2, а показано наглядное изображение трех взаимно перпендикулярных плоскостей проекций:
Плоскости проекций, пересекаясь в пространстве, делят пространство на восемь частей, которые называют октантами. Слева от плоскости проекций W располагаются 1, 2, 3 и 4 октанты, пронумерованные против часовой стрелки. Для получения изображений предмет располагают в 1-м октанте (европейская система) между наблюдателем и плоскостью проекций и проецируют его на каждую из взаимно перпендикулярных плоскостей проекций H, V и W, построив соответственно горизонтальную, фронтальную и профильную проекции предмета.
В качестве объекта проецирования на рис. 1.2, а взята точка А и построены ее прямоугольные проекции на каждую плоскость проекций:
Плоскости проекций пересекаются между собой по линиям, которые называют осями проекций: ось x, ось y и ось z.
Оси проекций принимают за оси координат, определяющих положение точки в пространстве, и называют системой прямоугольных координат x, y и z. Оси проекций пересекаются в точке О – это точка начала координат.
Расстояния точки А от каждой плоскости проекций определяют ее положение в пространстве и называются ее прямоугольными координатами:
Чтобы перейти от наглядного изображения системы трех плоскостей проекций H, Y и W и получить чертеж (эпюр), плоскости проекций первого октанта повертывают относительно координатных осей и совмещают с фронтальной плоскостью проекций V следующим образом:
Чертеж предмета содержит изображения проекций этого предмета.
Проекции предмета строятся как проекции совокупного множества точек, определяющих и задающих поверхность этого предмета. Точки объединяются в более общие известные из геометрии элементы: прямые, плоскости и различные поверхности (гранные, цилиндрические, конические и т. д.).
Чертеж точки содержит ее проекции, которые строятся по координатам этой точки.
На рис. 1.2, б показано построение чертежа произвольной точки А, заданной на рис. 1.2, а, положение которой в пространстве определяют координаты xA, yA и zA. Для построения чертежа этой точки выполнены следующие графические действия:
. Запомните! Горизонтальная A’ и фронтальная A» проекции точки лежат на одной вертикальной линии, перпендикулярной оси x, которая называется линией связи.
Чтобы построить профильную A'» проекцию точки, следует провести горизонтальную линию связи, перпендикулярную оси проекций z, и отложить от полученной точки Az отрезок AzA'», равный координате yA (или отложить от точки О вправо по оси y отрезок OAy = yA и провести вертикальную линию до пересечения с линией связи от фронтальной проекции точки А(A»).
. Запомните! Фронтальная A» и профильная A'» проекции точки лежат на одной горизонтальной линии связи, перпендикулярной оси проекций z.
На рис. 1.3 показано построение чертежа точки В(20,10,25) по заданным (в скобках) координатам x, y и z в миллиметрах. Выполнены следующие графические построения:
Структуризация материала первой лекции в рассмотренном объеме схематически представлена на рис. 1.4 (лист 1). На последующих листах 2 и 3 повторно приведены иллюстрации к этой схеме, способствующие закреплению изученного материала и его быстрому визуальному повторению (рис. 1.5 и 1.6).
Метод проекций. Образование чертежа по Г. Монжу.
Проекции точки :
Аппарат проецирования: объект проецирования; плоскость проекций; направление проецирующих лучей.
Проекции называют центральными, если проецирующие лучи исходят из одной точки, называемой центром проекций S.
Проекции называют параллельными, если проецирующие лучи параллельны (центр проекций удален в бесконечность).
Параллельные проекции могут быть:
Точки обозначаются прописными буквами латинского алфавита A, B, C, … и т.д., или арабскими цифрами 1, 2, 3, … и т.д. Проекции точек обозначаются теме же буквами, или цифрами, но со штрихами: A(A’,A»,A»’) и т.д.; 1(1′,1»,1»’), 2(2′,2»,2»’) и т.д.
Линии обозначаются строчными латинскими буквами: l, k, m, n и т.д. Их проекции
обозначаются теме же буквами, но со штрихами: l(l’,l»,l»’), k(k’,k»,k»’) и т.д.
Плоскости обозначаются греческими буквами: α, β, φ, δ и т.д. Их проекции обозначаются теме же буквами, но со штрихами: α(α’,α»,α»’), β(β’,β»,β»’) и т.д.
Центральное проецирование
Параллельное проецирование
Косоугольное параллельное проецирование имеет место при φ≠90°
Прямоугольное (ортогональное) параллельное проецирование имеет место при φ=90°
Метод Г. Монжа:
прямоугольное (ортогональное) параллельное проецирование на взаимоперпендикулярные плоскости проекций
Основные понятия метода проекций
Начертательная геометрия и техническое черчение входят в число дисциплин, составляющих основу инженерного образования. Курс начертательной геометрии сводится к изложению методов решения различных геометрических задач, используя основные положения начертательной геометрии. В каждой задаче студент должен самостоятельно наметить ход решения задачи и дать ему нужное графическое оформление. Необходимые навыки приобретаются в процессе самостоятельной работы. Настоящее пособие содержит материал, необходимый при подготовке к практическим занятиям по начертательной геометрии для студентов 1 курса инженерных специальностей, изучающих курсы «Инженерная графика и начертательная геометрия», «Инженерная и машинная графика». Поскольку все задачи решаются графически, оформление должно быть тщательным. Степень точности решения задач определяется точностью графических построений.
Автор настоящего методического пособия постарался отразить в нем те разделы начертательной геометрии, которые предусмотрены учебной программой курса «Инженерная графика» и изложить их как можно более доступно и компактно. Введем основные понятия метода проекций как основного при получении изображений на чертежах.
Основные свойства проекций:
Проецированием на одну плоскость проекций получается изображение, которое не позволяет однозначно определить его форму и размеры. Наличие одной проекции создает неопределенность изображения. В таких случаях говорят о необратимости чертежа, т.е. по такому чертежу невозможно воспроизвести оригинал. На практике применяют различные способы дополнения однопроекционного чертежа. В курсе начертательной геометрии, главным образом, рассматриваются чертежи, получаемые ортогональным проецирование на две или более взаимно перпендикулярные плоскости проекций (комплексные чертежи или эпюры). Другим способом получение обратимого чертежа является перепроецирование вспомогательной проекции предмета на основную аксонометрическую плоскость проекций аксонометрические чертежи, способы получения которых в данном пособии не рассмотрены.
Эпюр точки
При этом в начертательной геометрии приняты следующие обозначения и наименования:
Линии, связывающие пары проекций, называются линиями связи. Чертеж, изображенный на рис.2, называется трехпроекционным чертежом точки. Можно заметить, что:
Так как для описания положения точки в пространстве с помощью комплексного чертежа вполне достаточно двух ее проекций (обычно горизонтальной и фронтальной), в задачах начертательной геометрии используют двухпроекционное изображение точки на эпюре (рис.3).
Пример решения задачи на построение эпюра точки
Построить ортогональные (эпюр, двухпроекционный чертеж) и аксонометрические проекции точек 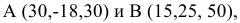
Решение
Для определения искомых координат точек, симметричных относительно геометрических объектов заданным, удобно использовать аксонометрическое изображение плоскостей 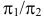
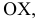
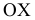
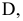
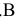
Подобное представление удобно для установления связи координат искомых точек 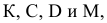
В истинности выражений (1) предлагается убедиться самостоятельно.
Эпюр прямой
Прямая линия вполне определена двумя своими точками (не совпадающими). Проекциями прямой линии в общем случае являются также прямые линии (рис.10).
Виды прямых. Прямая, произвольно расположенная в пространстве, носит название прямой общего положения. Прямые, определенным образом расположенные по отношению к плоскостям проекций носят название прямых частного положения, среди которых следует выделить (рис.11):
Принадлежность точки прямой линии. Если точка принадлежит прямой в пространстве, то проекции этой точки на эпюре будут принадлежать одноименным проекциям прямой (точка С на рис.11). При ортогональном проецировании сохраняется свойство пропорциональности длин: в каком отношении точка делит отрезок прямой в пространстве, в таком же отношении ее проекции делят одноименные проекции отрезка.
Только для горизонтальных, фронтальных, а также проецирующих прямых длину отрезка и углы его наклона к плоскостям проекций можно определить по эпюру. Прямая, параллельная плоскости проекций, проецируется на эту плоскость без искажения.
Взаимное положение прямых. Прямые в пространстве могут быть параллельными, пересекающимися и скрещивающимися, если прямые в пространстве параллельны, то на эпюре одноименные проекции этих прямых параллельны. Если прямые пересекаются, то на эпюре одноименные проекции прямых пересекаются и проекции точки пересечения лежат на одной линии связи. Если две прямые в пространстве скрещиваются, то их одноименные проекции могут пересекаться в точках, не лежащих на одной линии связи.
Прямой угол проецируется без искажения, если хотя бы одна из сторон прямого угла параллельна плоскости проекций (теорема о проецировании прямого угла).
Пример №1
Определить натуральную величину отрезка прямой и углы его наклона к плоскостям проекций (метод прям угольного треугольника).
Пример №2
Разделить отрезок 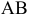
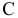
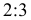
Для того, чтобы построить точку 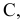
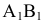
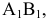
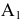
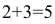
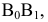
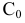
Пример №3
Достроить отрезок 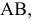
Для того чтобы достроить фронтальную проекцию точки 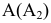
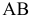
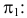
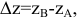
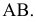
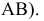
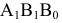
Пример №4
На прямой 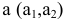
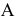
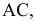
На прямой 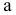
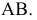
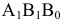
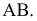
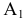
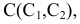
Пример №5 (Задача на профильные прямые).
Достроить прямую 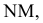
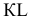
Замечание. Задачи на профильные прямые могут быть решены различными методами, в частности, с помощью построения третьей проекции этих прямых, либо с помощью методов косоугольного параллельного проецирования путем построения, так называемых, вспомогательных прямых. К этому типу задач следует отнести задача по определению взаимного положения профильных прямых, построения точки пересечения профильных прямых, а также ряд позиционных задач, связанных с построением точек пересечения профильной прямой и плоскости. Приведем решение задачи на профильные прямые методом построения вспомогательных прямых.
Для того, чтобы построить недостающую фронтальную проекцию 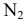
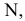
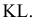
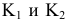
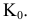
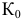
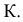
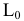
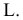

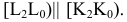
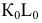
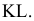
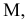
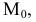
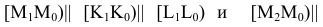
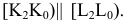
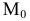
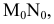
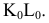
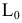
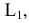
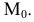
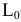
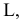
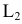
Плоскость
Плоскость в пространстве однозначно определена тремя точками, не лежащими на одной прямой. В связи с этим существует несколько способов задания плоскости на эпюре, среди которых отметим следующие (рис.31):
Виды плоскостей. Плоскость, произвольно расположенная в пространстве (по отношению к плоскостям проекций), называется плоскостью общего положения. Все плоскости, изображенные на рис.31 являются плоскостями общего положения.
Плоскость, перпендикулярная одной или двум плоскостям проекций, называется плоскостью частного положения, причем плоскость перпендикулярная одной из плоскостей проекций носит название проецирующей плоскости: горизонтально проецирующей, если 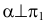
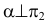
Прямая принадлежит плоскости, если:
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости.
Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой. Если параллельны две проецирующие плоскости, то на эпюре параллельны из одноименные следы.
Две плоскости пересекаются по прямой линии. Для построения линии пересечения двух плоскостей достаточно построить две точки, принадлежащей одновременно двум заданным плоскостям. Для построения линии пересечения двух плоскостей общего положения обычно используют метод вспомогательных секущих плоскостей.
Пример №6
Достроить плоский четырехугольник (рис.34).
Пример №7
Достроить точку 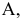
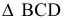
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости. Через известную проекцию точки 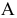
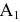
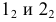
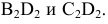
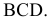
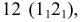
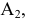
Пример №8
Через заданную точку 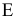
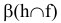
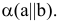
Пример №9
Построить линию пересечения двух плоскостей: плоскости общего положения 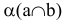
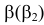
Пример №10
Построить линию пересечения двух плоскостей общего положения: 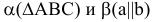
При решении этой задачи используется метод секущих плоскостей. Так как две плоскости пересекаются по прямой линии, определяемой двумя точками, для построения необходимо ввести две дополнительные секущие плоскости. Порядок решения задачи:
1. Вводим дополнительную секущую плоскость 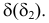
2. Строим линию пересечения фронтально-проецирующей плоскости 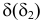
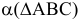
3. Строим линию пересечения фронтально-проецирующей плоскости 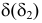
4. Строим точку 
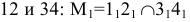
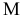
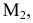
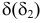
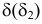
5. Аналогично строится вторая точка, принадлежащая линии пересечения 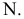
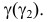
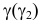
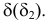
6. После построения точки 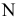
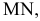
Пример №11
Построить линию пересечения двух плоскостей общего положения 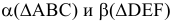
Задача решается аналогично предыдущей. Для уменьшения количества вспомогательных построений в качестве секущих введены плоскости 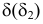
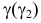
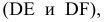
Взаимное положение прямой и плоскости
Прямая может лежать в плоскости, пересекаться о плоскостью и быть параллельна плоскости.
Если прямая параллельна проецирующей плоскости, то на эпюре будут параллельны одноименные проекции прямой и следа плоскости.
Если прямая параллельна плоскости общего положения, то она должна быть параллельна какой-либо прямой в этой плоскости.
Точка пересечения прямой и проецирующей плоскости на эпюре определяется как точка пересечения одноименных проекций и следа плоскости.
Точка пересечения прямой и плоскости общего положения определяется с помощью метода вспомогательных секущих плоскостей в следующем порядке:
Если прямая перпендикулярна плоскости, то она должна быть перпендикулярна двум пересекающимся прямым плоскости, например, главным линиям плоскости, горизонтали 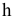
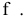
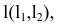
Две плоскости взаимно перпендикулярны, если в одной из них можно провести прямую, перпендикулярную другой плоскости.
Две прямые взаимно перпендикулярны, если одна из них лежит в плоскости, перпендикулярной второй прямой.
Пример №12
Найти точку пересечения прямой 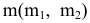
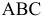
Через прямую 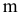
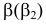
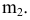
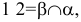
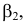
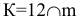
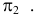
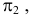
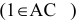
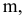
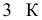
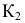
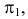
Пример №13
Построить перпендикуляр к плоскости 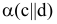
Перпендикуляр 1 к плоскости можно восстанавливать из любой ее точки, например, из точки 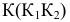
Для того, чтобы отложить на отрезке 1 заданную длину 30 мм, первоначально задаются произвольной отрезком 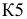
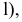
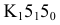
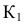
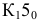
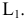
Пример №14
Определить расстояние от точки 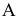
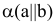
Задача решается в три этапа:
Пример №15
Через точку 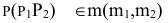
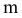
Через точку 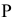
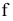
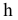
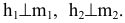
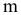
Метод перемены плоскостей проекций
Суть метода состоит в том, что при неизменном положении рассматриваемого объекта в пространстве, заменой одной или последовательно двух плоскостей проекций можно перевести геометрический объект в частное положение и тем самым облегчить решение задач.
С помощью данного метода, путем замены одной плоскости проекций можно:
Большинство метрических и позиционных задач достаточно просто решаются с использованием метода перемены плоскостей проекций.
Пример №16
Определить натуральную величину отрезка прямой и углы его наклона к плоскостям проекций 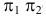
Произведем замену 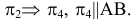
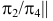
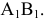
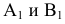
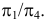
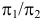
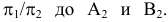
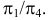
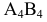
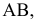
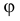
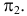
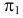
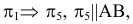
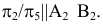
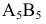
Пример №17
Определить расстояние от точки 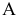
Чертеж преобразовывается таким образом, чтобы плоскость 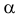
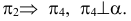
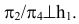
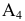
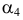
Пример №18
Определить натуральную величину треугольника 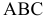
Для решения задач подобного типа необходимо выполнить две замены:
В результате первой замены плоскость переводится в частное положение и спроецируется в линию 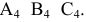
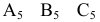
Поверхности. Сечение поверхностей плоскостями частного положения
Поверхность представляет собой множество последовательных положений линии, перемещающейся в пространстве. Эту линию называют образующей. Закон перемещения образующей может быть задан тоже линиями. Эти линии называются направляющими. Гранные поверхности образуются перемещением прямолинейной образующей 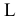
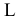
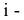
Вид поверхности зависит от формы образующей линии и от закона перемещения ее в пространстве вдоль направляющей. Точку на гранной поверхности можно построить с помощью образующей, проходящей через эту точку (рис.82).
Каждая точка образующей поверхности вращения описывает окружность, плоскость которой перпендикулярна оси вращения. Такие окружности называются параллелями. Кривые на поверхности вращения, образующиеся в результате пересечения поверхности вращения плоскостями, проходящими через ось вращения, называются меридианами. Строить точки на поверхности вращения удобнее всего с помощью параллелей (рис.83).
Линия сечения поверхности проецирующей плоскостью строится по точкам пересечения образующих поверхности или ее параллелей с плоскостью. Для гранных тел линией сечения будет ломаная, построенная на эпюре по точкам пересечения следа проецирующей плоскости с ребрами гранной поверхности. Если даны тела вращения, то для решения задачи нужно выбрать несколько, принадлежащих следу секущей плоскости, точек, провести через выбранные точки параллели (или образующие), определить точки пересечения их со следом секущей плоскости; построить по ним лекальную кривую сечения. При этом в первую очередь следует определить характерные точки линии сечения на очерковых образующих (наиболее близкие, наиболее удаленные и др.).
Пример №19
Построить сечение пирамиды 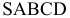
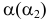
Пример №20
Построить сечение конуса фронтально-проецирующей плоскостью в трех проекциях (рис.85).
Секущая плоскость пересекает две образующие конуса, поэтому в сечении получится эллипс (часть его). Характерные точки сечения получатся в результате пересечения очерковой образующей конуса со следом секущей плоскости (точка 1), и окружностью основания. Дополнительные точки сечения можно получить, выбрав ряд точек, принадлежащих следу секущей плоскости, построив их затем на поверхности конуса с помощью образующих или с помощью параллелей. Для эллипса сечения необходимо также определить
Пример №21
Построить в трех проекциях геометрическое тело с вырезом части (рис.86).
При решении задач подобного типа необходимо предварительно проанализировать вид секущих плоскостей. Если вырез строится для гранного тела, то необходимо строить точки пересечения следов секущих плоскостей с ребрами гранного тела, а также точки пресечения следов секущих плоскостей между собой (эти точки обычно принадлежат граням тела). Для удобства построения точки желательно пронумеровать по порядку. После построения точек, принадлежащих либо граням, либо ребрам тела на всех проекциях, точки соединяют в необходимой последовательности прямыми линиями. После этого необходимо оформить чертеж окончательно, учитывая видимость и невидимость вновь образованных ребер.
Если вырез строится для тела вращения, необходимо выяснить, какая кривая будет являться результатом сечения той или иной плоскостью заданного тела. Необходимо, прежде всего, строить точки пересечения следов секущих плоскостей, а затем ряд дополнительных точек, принадлежащих следам. После построения выбранных точек на всех проекциях, их плавно соединяют. Затем необходимо окончательно оформить чертеж, учитывая видимость вновь
Взаимное пересечение поверхностей вращения
Линия пересечения двух поверхностей в общем виде представляет собой пространственную кривую, которая может распадаться на две части и более. Обычно линию пересечения поверхностей строят по отдельным точкам. Сначала определяют опорные точки в пересечении контурных линий каждой поверхности с другой. Опорные точки позволяют видеть, в каких пределах расположены проекции линии пересечения и где между ними имеет смысл определить промежуточные точки. При этом нужно иметь в виду, что проекции линии пересечения всегда располагаются в пределах площади наложения одноименных проекций пересекающихся поверхностей.
Общим способом построения точек линии пересечения двух поверхностей является метод вспомогательных секущих плоскостей. Суть метода состоит в следующем. Вводятся вспомогательные секущие проецирующие плоскости. Вспомогательная плоскость пересекает данные поверхности по линиям (желательно, графически наиболее простым). В пересечении этих линий получаются точки, принадлежащие обеим поверхностям, т.е. точки их линии пересечения. Секущие плоскости обычно выбираются частного положения.
Пример №22
Построить линию пересечения поверхности конуса и сферы методом вспомогательных секущих плоскостей (рис.91).
Сначала отмечаем очевидные общие точки двух поверхностей 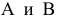
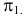
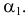
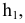
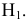
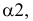
Пример №23
Построить линию пересечения поверхности конуса и сферы методом вспомогательных секущих плоскостей (рис.92).
Определение наивысшей и наинизшей точек линии пересечения
Если пересекающиеся поверхности вращения не имеют общей фронтальной плоскости симметрии, то опорные точки (наивысшую и наинизшую) линии пересечения этих поверхностей можно определить, используя метод перемены плоскостей проекций, как показано на рис. 92. При этом происходит замена плоскости 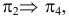
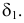
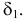
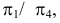
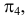
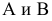
Начертательная геометрия и ее методы находят применение в различных областях науки н техники: в машиностроении, архитектуре, строительстве, изобразительном искусстве.
Основным методом проецирования является ортогональное проецирование. Этот метод основан на проецировании пространственного объекта на две взаимно перпендикулярные плоскости лучами, перпендикулярными (ортогональными) к этим плоскостям.
В строительстве и машиностроении применяется также аксонометрическое проецирование. Изображения (чертежи), полученные с помощью такого проецирования, имеют высокую наглядность и простые построения
При проектировании крупногабаритных инженерных сооружений (строительных площадок, каналов, плотин, откосов железных и автомобильных дорог, насыпей и выемок на кривых и прямых участках пути), при изыскании и трассировании дорог, для определения границ и объемов земляных работ при строительстве этих сооружений, то есть когда длина сооружения намного превышает высоту, применяют метод проекций с числовыми отметками.
В строительстве и архитектуре при изображении проектируемых промышленных и жилых зданий, городских площадей и улиц, железнодорожных вокзалов, интерьеров станций метрополитенов и пассажирских залов, мостов и путепроводов, различных дорог широко используются перспективные проекции.
Эти проекции дают возможность получить наглядные изображения инженерных сооружений, которые наиболее точно передают реальное зрительное восприятие человека.
В начертательной геометрии чертежи являются тем инструментом, с помощью которого осуществляется непосредственное изучение геометрических форм предмета и выполняется решение пространственных задач. Поэтому к чертежам предъявляют следующие требования:
Чертежи, выполненные методом проецирования, называются проекционными.
Начертательная геометрия возникла в глубокой древности. Потребность в изображениях пространственных форм на плоскости, развитие изобразительного искусства, техники пред определили появление начертательной геометрии.
Ученые всего мира внесли большой вклад в развитие методов построения изображений пространственных форм на плоскости. Это великий греческий геометр Эвкпид (Ш в. до н.э.), римский архитектор Витрувий (I в. до н.э.).
В России практические приемы построения графических изображений были известны еще в давние времена. Рисунки домов, крепостей в различных древних летописях сохранили для нас достаточно совершенные для своего времени примеры изображений.
Работы таких великих русских мастеров, как иконописец Рублев, меха ник-самоучка И.П. Кулибин, зодчие Д.В. Ухтомский, В.И. Баженов, М.Ф. Казаков и многие другие, являются образцами правильных проекционных изображений.
В 1798 году Гаспар Монж опубликовал свой главный научный труд «Начертательная геометрия».
Значительный вклад в развитие начертательной геометрии внесли русские ученые: Н.И. Макаров, В.И. Курдюмов, Н.А. Рынин, А.И. Добряков, Н.Ф. Четверухин и многие другие.
Позднее продолжили свои исследования такие ученые, как В.О. Гордон, С.А. Фролов, А.В. Бубенников, Н.Н. Крылов и др.
Пример центрального проецирования
Пусть в пространстве задана плоскость 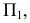
Выберем какую-либо точку 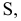
Заданную точку 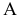
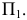
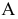
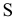
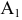
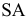
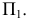
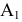
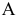
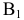
Очевидно, что каждой точке пространства будет однозначно соответствовать своя собственная проекция. Однако на рис 1.2 мы видим, что проекцией точки 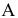
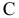
Следовательно, такое изображение не является взаимно однозначным, и судить о положении точек 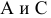
Пример параллельного проецирования
Если центр проецирования 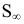
Проецирующие лучи, исходящие из бесконечного далека, могут быть наклонены под любым углом к плоскости проекций.
При заданном аппарате проецирования можно построить параллельную проекцию любой точки пространства. Для этого через заданную точку 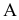
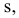
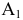
Через точку 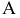
Точки 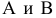
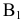
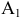
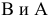
Пример ортогонального (прямоугольного) проецирования
Ортогональное (прямоугольное) проецирование является частным случаем параллельного проецирования, при котором направление проецирования 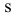
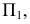
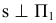
Такое проецирование является наиболее простым и удобным из всех других существующих видов проецирования. Оно обеспечивает простоту определения проекций геометрических объектов, а также позволяет сохранить на проекциях их форму и размеры.
Прямоугольное проецирование имеет те же недостатки, что и центральное и параллельное проецирование: одна прямоугольная проекция не дает возможности определить положение геометрического объекта в пространстве.
Для того чтобы получить так называемый «обратимый чертеж», который позволит определить любые геометрические параметры объекта, надо иметь хотя бы две связанные между собой прямоугольные проекции.
Пример проекции точки
Проецирование будем вести на три взаимно перпендикулярные плоскости (рис. 1.6):
Линии пересечения этих плоскостей называют осями проекций (координатными):
и рассматривают как систему прямоугольных декартовых координат с центром
Положение точки в пространстве определяется тремя координатами:
Для получения прямоугольных проекций точки 
Для получения более удобного чертежа необходимо совместить плоскости проекций 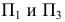
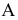
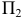
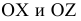
Прямая, которая соединяет на чертеже две проекции одной и той же точки, называется линией связи.
Расстояния от заданной точки 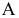
Каждая проекция точки определяется двумя координатами: 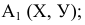
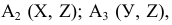
Если все три координаты точки отличны от нуля, точка находится в пространстве (см. рис. 1.6 и рис. 1.7).
Если одна из координат равна нулю, точка находится в плоскости проекций, например, точка 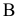
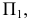
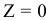
Если все три координаты равны нулю, точка совпадает с началом координат.
По двум известным проекциям всегда можно построить третью (рис. 1.9).
Например, чтобы построить профильную проекцию 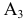
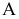
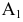
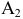
На рис. 1.11 построена горизонтальная проекция 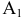
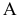
Пересекаясь между собой, плоскости 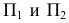
Три плоскости проекций делят пространство на восемь октантов. Нумерация октантов дана на рис. 1.17.
Совмещая плоскости проекций так же, как было показано ранее, можно получить чертеж точки, расположенной в любом из восьми октантов (рис. 1.18).
Считают, что наблюдатель, рассматривающий предмет, находится в 1-ом октанте.
Приняв для отсчета координат точки систему, показанную на рис. 1.17, составляют таблицу знаков координат во всех восьми октантах (табл.).
Любая точка пространства 
Пусть задана точка 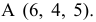
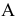
Построение изображения самой точки и ее проекций на пространственной модели осуществляют следующим образом: на осях координат от точки 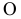
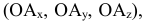
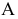
Эпюр точки представлен на рис. 1.20.
Виды проецирования
Правила построения изображений, излагаемые и инженерной графике, основаны на методе проекций, в том, что луч SA (рис.1), выходя из точки S, пересекает плоскость πi в точке Ai (SA∩ πi= А).
Рисунок 1
Проецированием называется процесс построения изображений путем проведения через характерные точки предмета проецирующих прямых до их пересечения с плоскостью проекций.
В зависимости от положения центра проецирования по отношению к плоскости проекций проецирование может быть центральным (коническим) или параллельным (цилиндрическим).
При центральном проецировании все проецирующие лучи, при проецировании системы точек или какой-либо фигуры, проходят через одну и ту же точку, называемую центром проекций.
Изображение треугольника Ai Bi Ci на плоскости πi называют центральной проекцией треугольника АВС (рис.2, а).
Изображение, полученное по способу центрального проектирования, называют перспективным изображением или перспективой.
Достоинством центрального проектирования является его большая наглядность, объясняемая свойством глаза, устроенного по принципу центрального проектирования (оптический центр хрусталика глаза — центр проекций, сетчатка — плоскость проекций).
Однако изображение предметов по методам центрального проектирования весьма сложно, при этом затрудняется простановка размеров, ухудшается возможность воспроизведения формы и размеров изображаемого предмета. Поэтому при составлении технических чертежей получил распространение метод параллельного проектирования.
Параллельное проецирование рассматривают как частный случай центрального проецирования, при котором центр проецирования удален в бесконечность.
Проекция называется параллельной, если все проецирующие лучи при проецировании системы точек или какой-либо фигуры параллельны какому-то заданному направлению S.
Изображение треугольника Ai Bi Ci на плоскости πi называют параллельной проекцией треугольника АВС (рис. 2,б).
Параллельные проекции бывают прямоугольные и косоугольные.
Если направление проецирования составляет с плоскостью проекций прямой угол, проекция будет прямоугольной (ортогональной); если этот угол острый, то она будет косоугольной.
Все чертежи выполняют по правилам прямоугольного (ортогонального проецирования).
Рисунок 2
Основные свойства параллельных проекций
1. Проекцией точки является точка (рис. 3).
2. Прямая проецируется в прямую (рис. 3).
Доказательство: прямая CD и проецирующие лучи CCi, DDi определяют плоскость, а плоскости пересекаются по прямой линии. Частный случай: Если прямая (EF) параллельна направлению проецирования (рис. 3), то ее проекцией является точка (точка Ei=Fi). Точки E и F, расположенные на одном проецирующем луче, называют конкурирующими точками.
Рисунок 3
3. Если точка принадлежит прямой (точка К принадлежит прямой АВ), то ее проекция принадлежит проекции этой прямой (Кi принадлежит AiBi) (рис.4)
Доказательство: прямая АВ и проецирующие лучи AAi, ВВi образуют плоскость AAiВВi, точка КеАВ 
4. Если две прямые параллельные, то их проекции параллельны между собой (рис. 5).
5. Отношение отрезков прямой линии равно отношению их проекций, т. е. АВ/АМ= AiBi/AiMi (рис. 5).
Доказательство: треугольники ВМВi и AMAi подобны, т.к. AAi||ВВ, следовательно AВ/AM = AiВ1 /AiMi.
6. Отношение отрезков двух параллельных прямых равно отношению их проекций (рис. 5).
Доказательство: так, AB||CD по условию, следовательно, ΔMВВi
ΔNDDi, так как сходственные стороны их параллельны. Учитывая свойство п.5, имеем AB/ CD = AiBi / CiDi.
Рисунок 5
Понятие о методе Г. Монжа
Французский математик Гаспар Монж (1746-1818г.г.), систематизировав и обобщив накопленные к тому времени знания по теории и практике построения изображений предметов пространства, предложил получать их изображения путем проецирования на две или три взаимно перпендикулярные плоскости проекций. Этот метод является основным методом при выполнении технических чертежей.
Требования, предъявляемые к чертежу:
Проецирование точки на две плоскости проекций
Плоскости проекций π1 и π2 образуют систему плоскостей π1 / π2.
Рисунок 6
Для того, чтобы получить прямоугольные (ортогональные) проекции некоторой точки A в системе π1 / π2, т. е. проекции на две плоскости проекций, надо из точки A провести проецирующие прямые, перпендикулярные плоскостям проекций π1 и π2, и точки пересечения этих прямых с плоскостями проекций дадут проекции точки A в системе
Плоскость AA2AxA1, проведенная через проецирующие прямые AA1 и AA2 перпендикулярна к плоскости π2 и к плоскости π1, так как она содержит перпендикуляры к этим плоскостям. Поэтому она перпендикулярна и к линии их пересечения, т. е. к оси проекций x. Эта плоскость пересекает плоскости π 1 /π 2 по двум взаимно перпендикулярным прямым A1Ax и A2Ax, пересекающимся в точке Ах на оси проекций.
Следовательно, проекции некоторой точки А в системе π1 / π2 располагаются на прямых, перпендикулярных к оси проекций и пересекающих эту ось в одной и той же точке.
Повернув плоскость π 1 вокруг оси x на угол 90° до совмещения с плоскостью π2, получим изображение (рис. 7), на котором проекции точки А — А1 и А2 окажутся на одном перпендикуляре к оси x — на линии проекционной связи.
Рисунок 7
Такое изображение, т. е. изображение, полученное при совмещении плоскостей проекций с плоскостью чертежа, называется эпюром (от французского слова epure — чертеж). На эпюре: A2Ax — расстояние точки А от плоскости π 1, A1Ax— расстояние точки A от плоскости π 2.
Проецирование точки на три плоскости проекций
Для суждения об относительном положении точки в пространстве необходимо и достаточно иметь проекции этих точек на две плоскости проекций (двухкартинный чертеж). Но на практике, в частности при изображении деталей машин, приходится прибегать к проецированию предмета на три плоскости проекций (трехкартинный чертеж).
На рис. 8 изображены три взаимно перпендикулярные плоскости проекций: π1, π2, π3.
Три взаимно перпендикулярные плоскости проекций образуют систему плоскостей π1, π2 , π3.
Линия пересечения двух каждых двух плоскостей называется осью проекций: ось X, ось Y и ось Z. Буквой О обозначается точка пересечения осей проекций.
Наглядное изображение на рис. 8 содержит горизонтальную А1, фронтальную А2 и профильную А3 проекции некоторой точки А.
Для получения чертежа (эпюра) точки А совмещаем плоскости проекций π1, π3 с плоскостью π2, (повернем плоскости π1, π3. на угол 90° в направлении, указанном стрелками на рис. 8). При этом ось y (рис. 9) как бы раздвоилась: одна ее часть с плоскостью π1 опустилась вниз (на чертеже обозначена буквой y), а вторая с плоскостью π3 ушла вправо (на чертеже обозначена буквой y1).
Рисунок 8
Рисунок 9
Все проекции связаны между собой линиями проекционной связи.
Отрезки проецирующих лучей от точки А до плоскостей проекций называют координатами точки А:
Так как положение точки в пространстве полностью определяется ее проекциями на две взаимно перпендикулярные плоскости проекций, то по двум проекциям точки всегда может быть построена ее третья проекция.
Положение профильной проекции по двум заданным горизонтальной и фронтальной может быть определено (рис. 10):
Рисунок 10
Задание и изображение прямой. Положение прямой относительно плоскостей проекций
Для построения эпюра отрезка прямой АВ достаточно построить проекции двух точек — точек А и В, и одноименные проекции соединить линиями (рис. 11).
Рисунок 11
Относительно плоскостей проекций прямая может занимать различные положения:
На рис. 11 дан эпюр отрезка прямой общего положения, т.к. точки А и В данного отрезка находятся на разных расстояниях от плоскостей проекций.
Прямая, параллельная какой-либо плоскости проекций называется прямой уровня. Горизонтальная прямая (горизонталь) параллельна плоскости π1. Фронтальная прямая (фронталь) параллельна плоскости π2. Профильная прямая параллельна плоскости π3.
В таблице 1 приведены чертежи прямых частного положения.

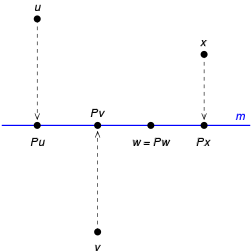
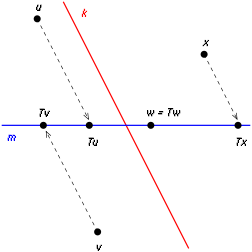

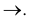
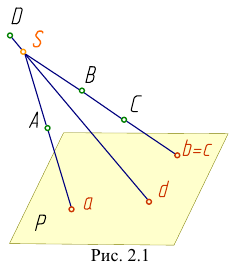
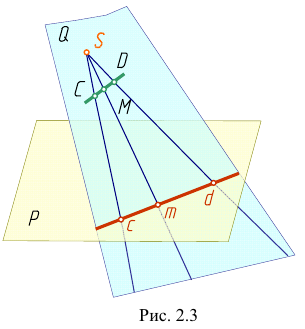
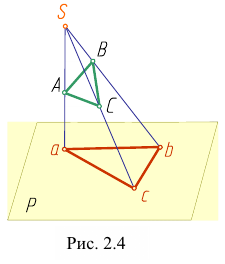
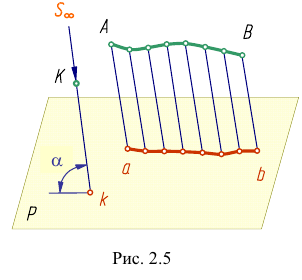
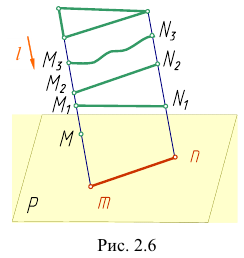
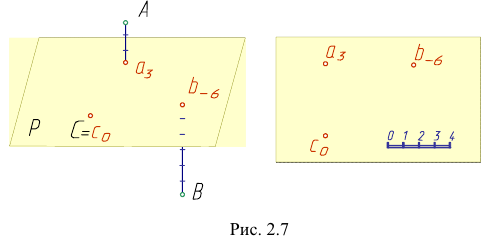
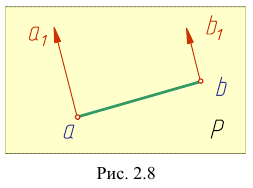
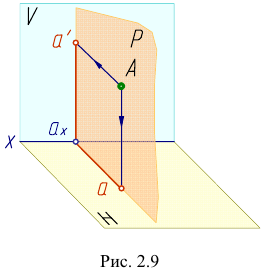
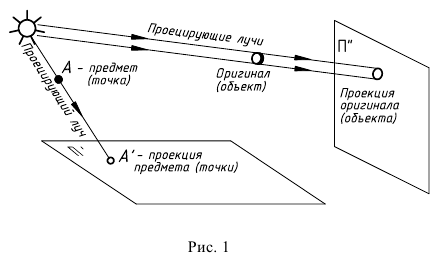
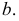
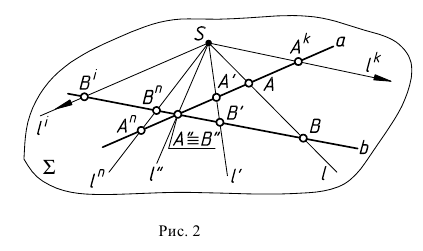
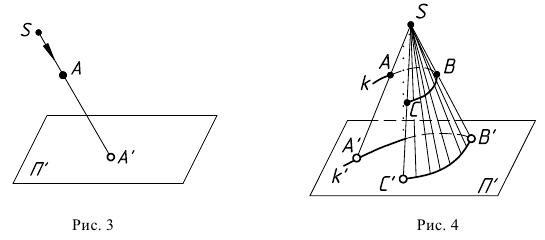
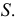
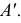
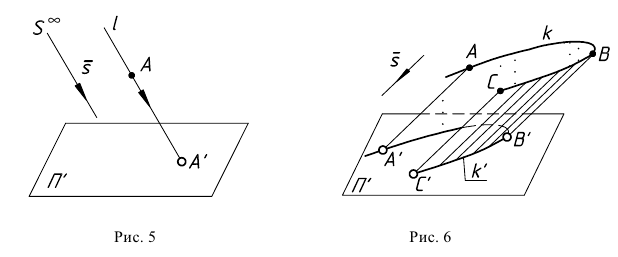
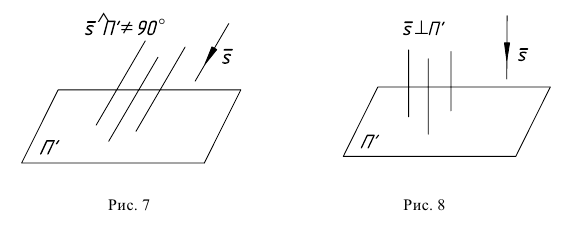
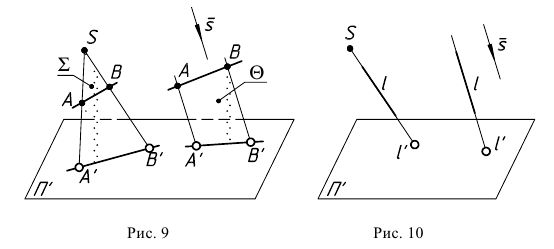
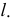
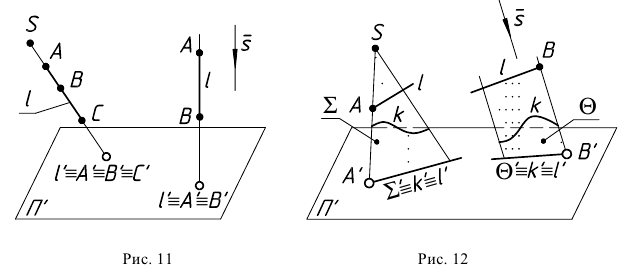
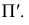
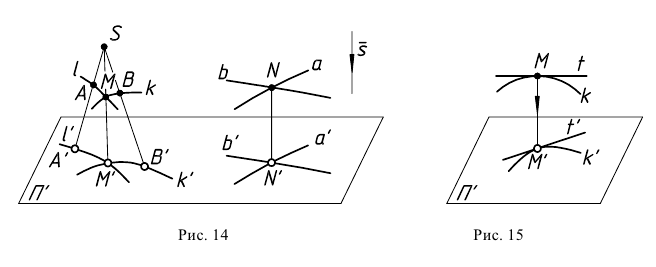
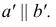
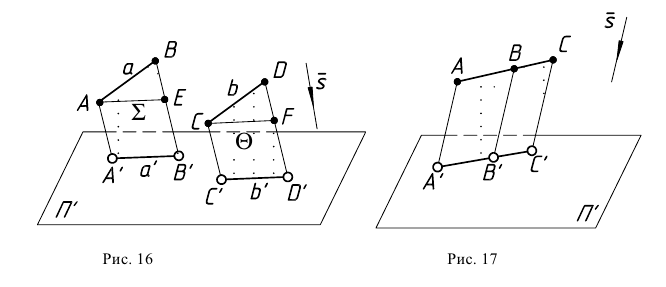
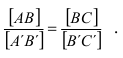
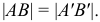
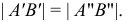
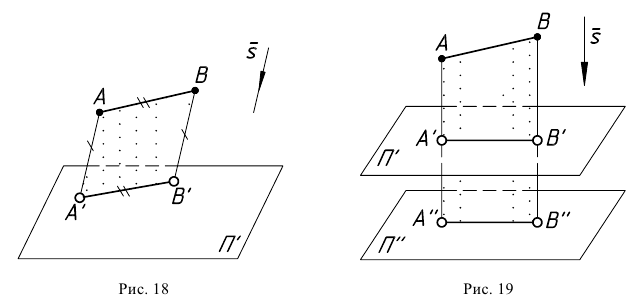
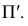
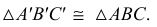
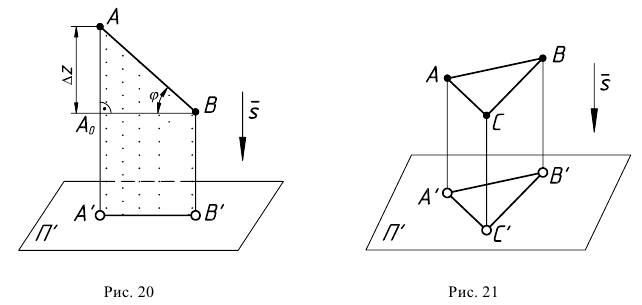
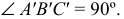
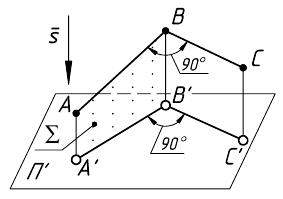
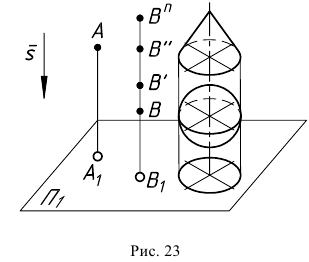
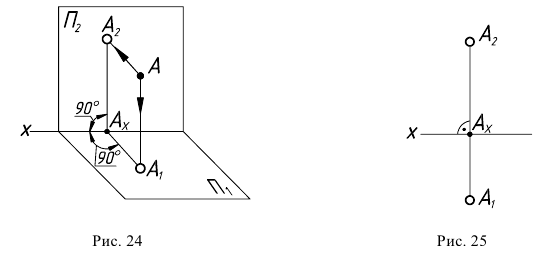
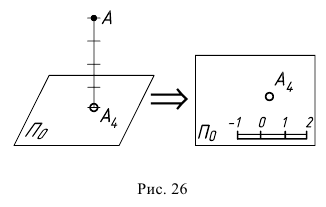
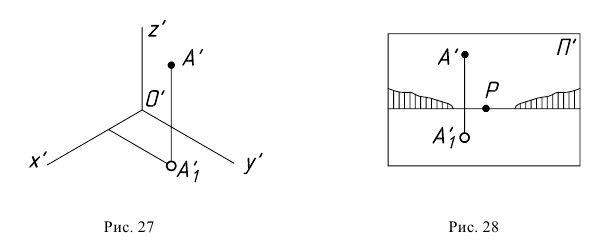
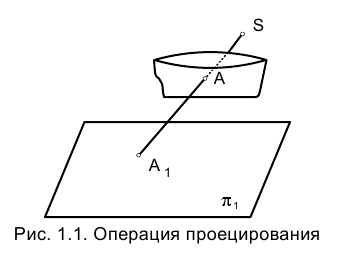
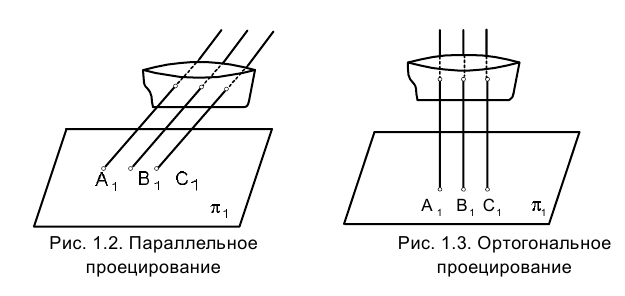
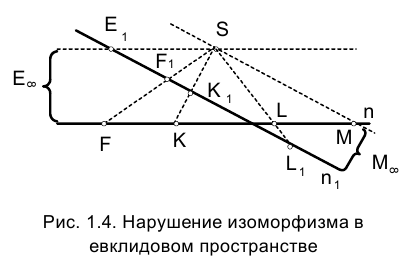
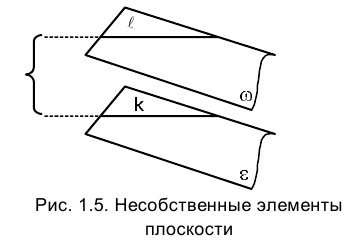
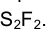
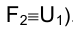
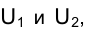
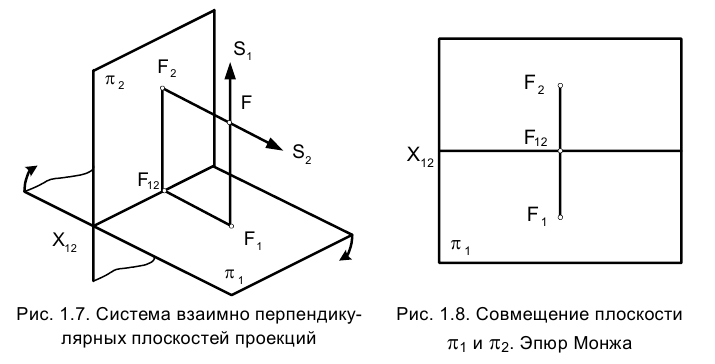
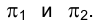
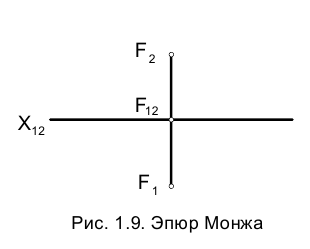
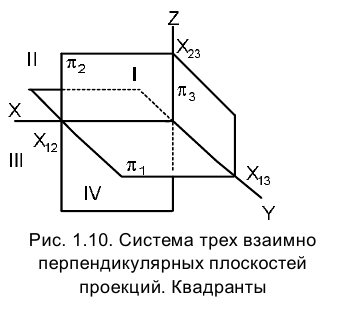
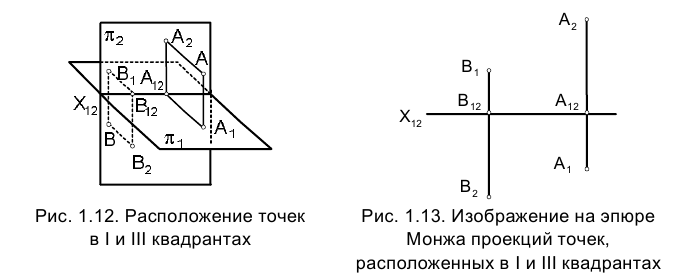
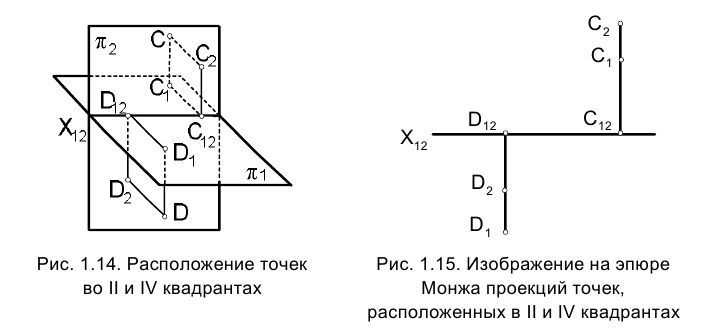
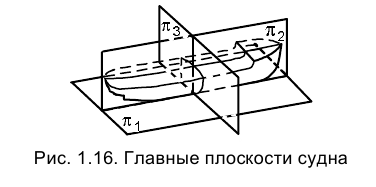
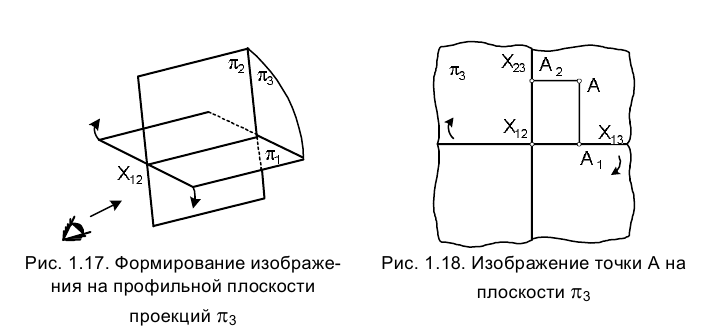
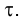
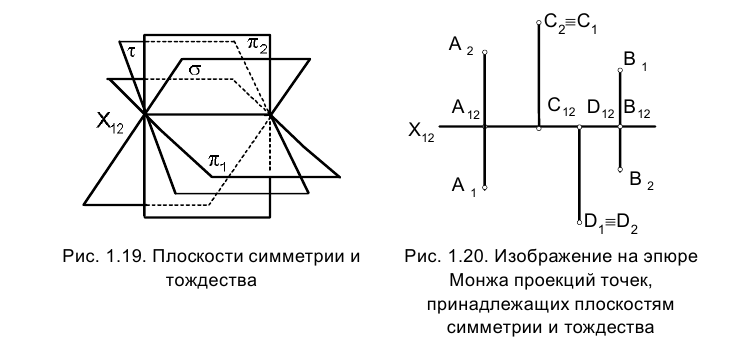
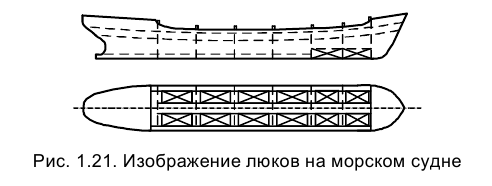
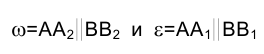
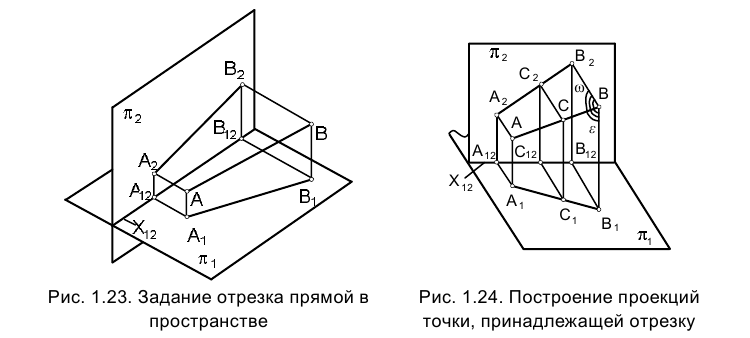
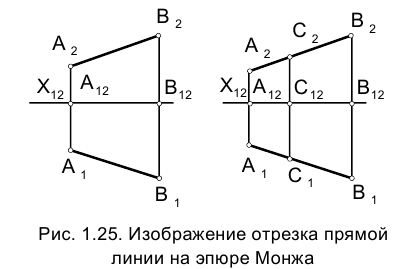
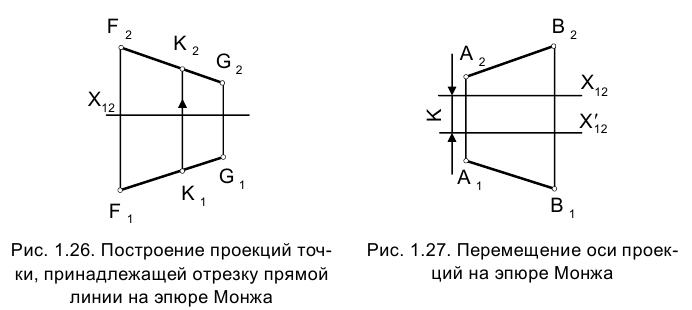
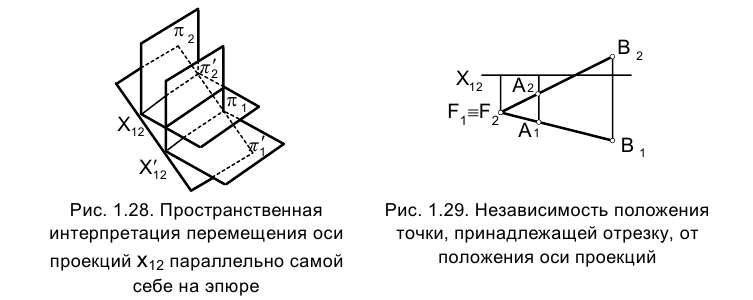
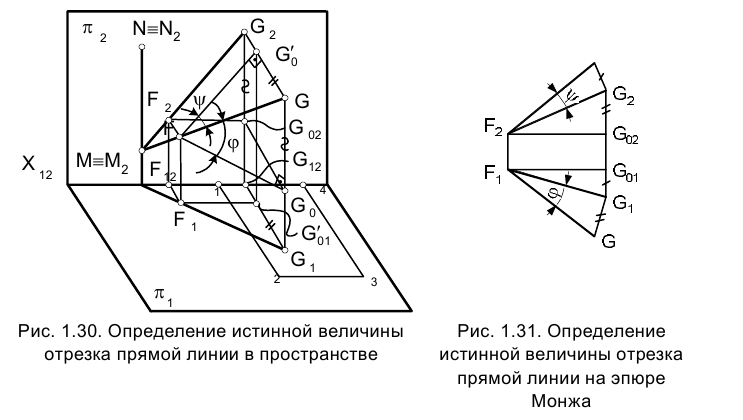
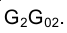
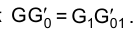
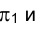
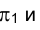
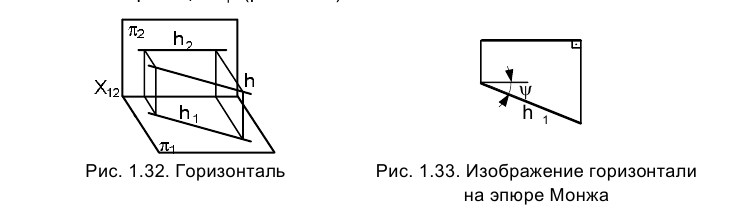
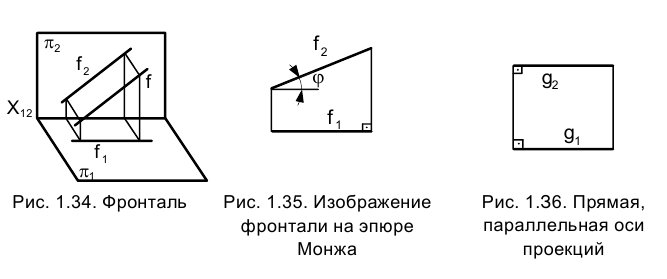
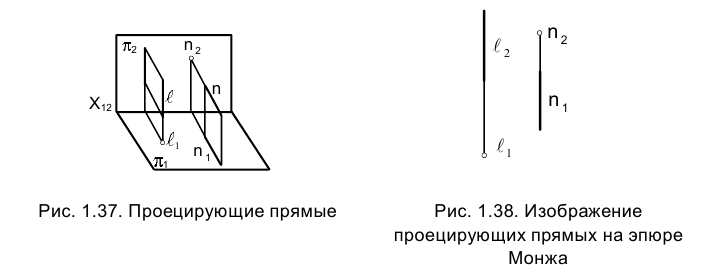
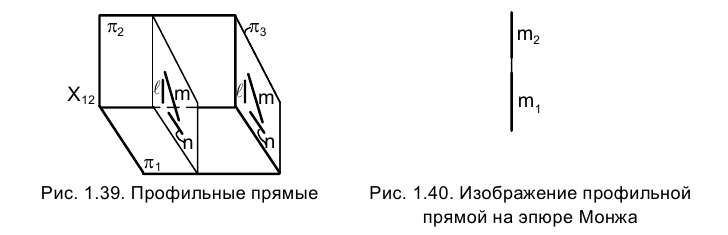
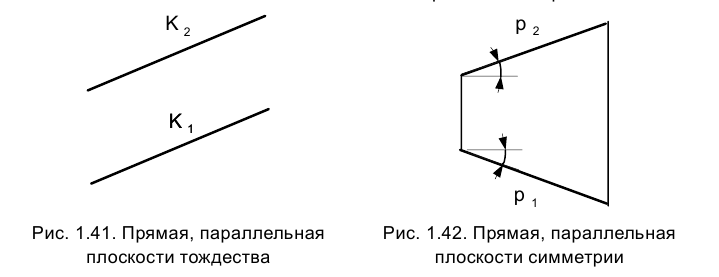
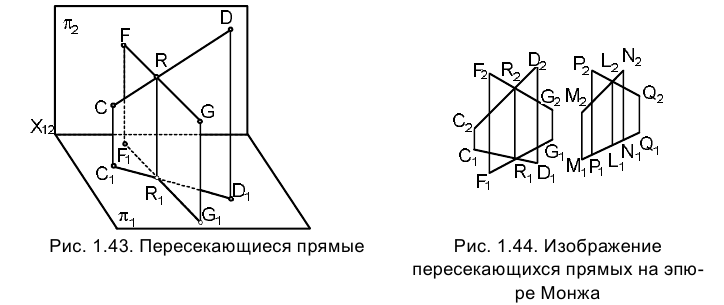
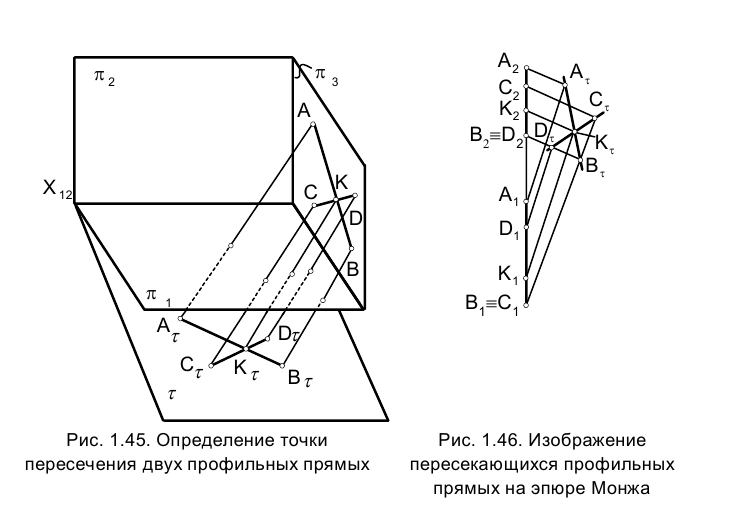
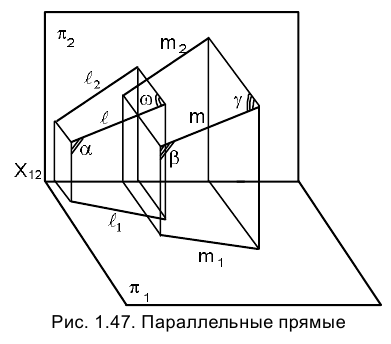
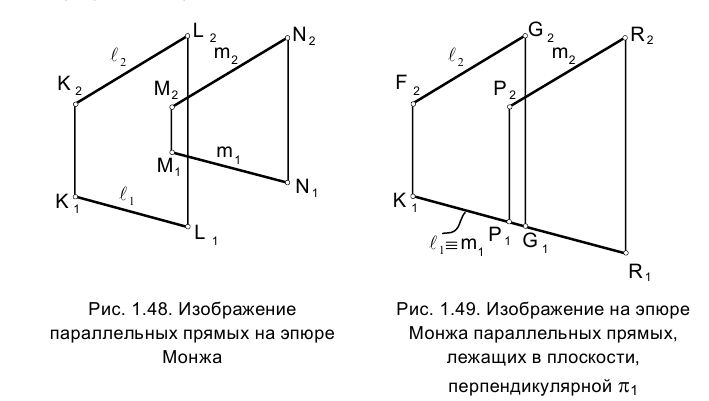
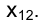
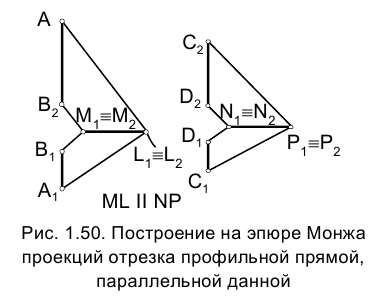
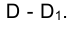
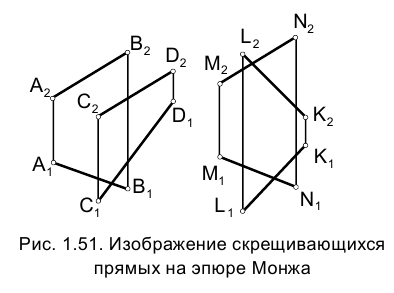
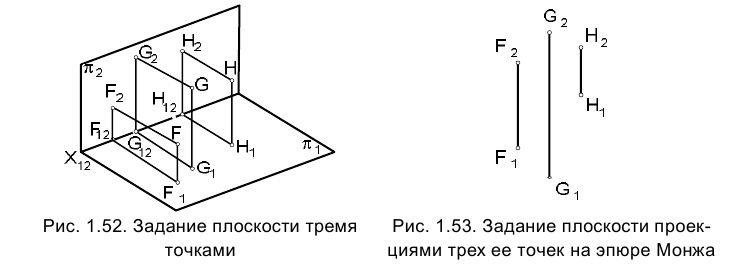
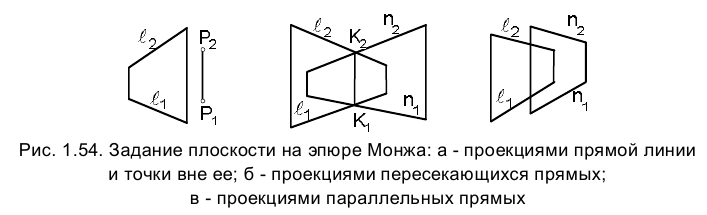
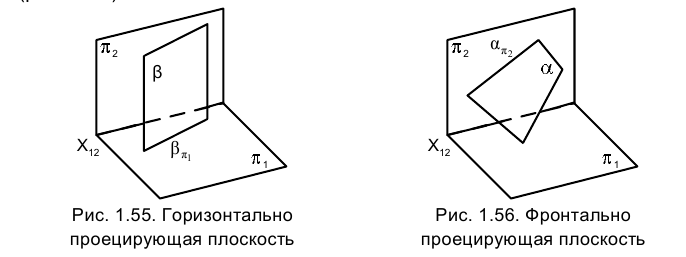
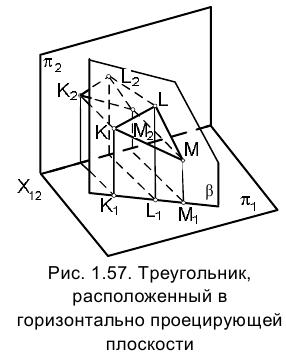
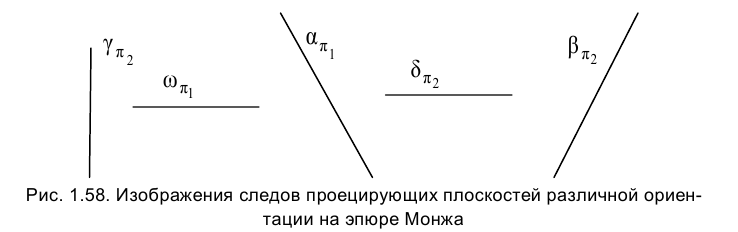
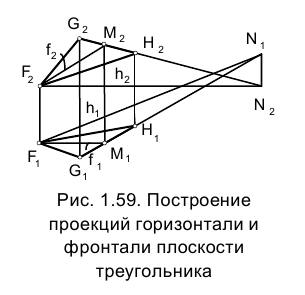
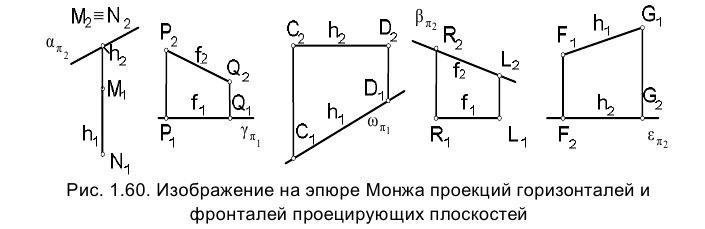
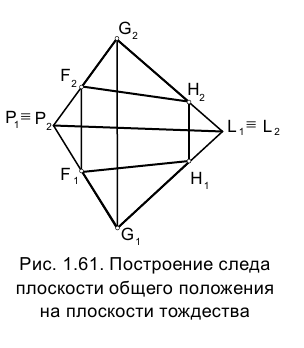
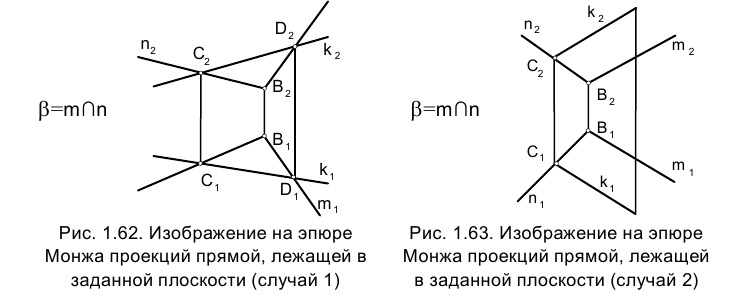
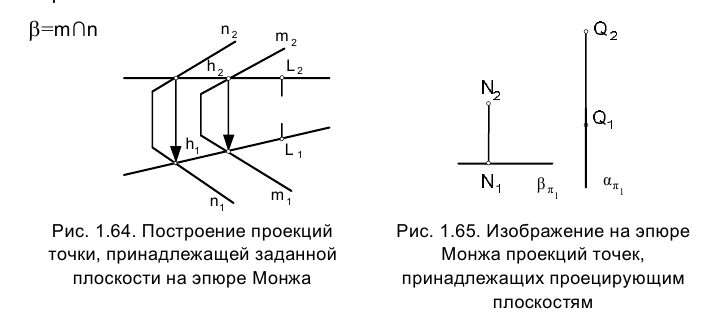
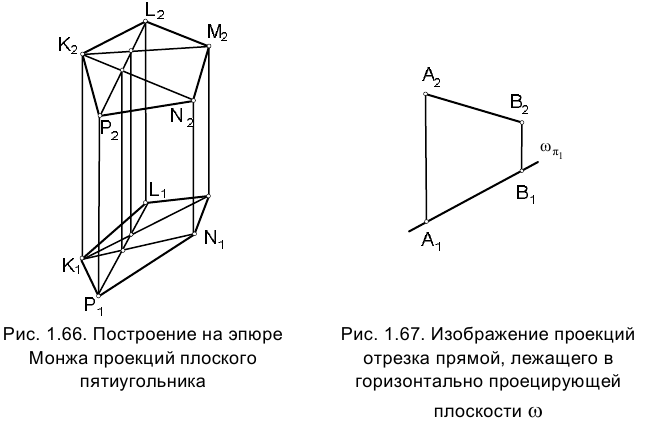
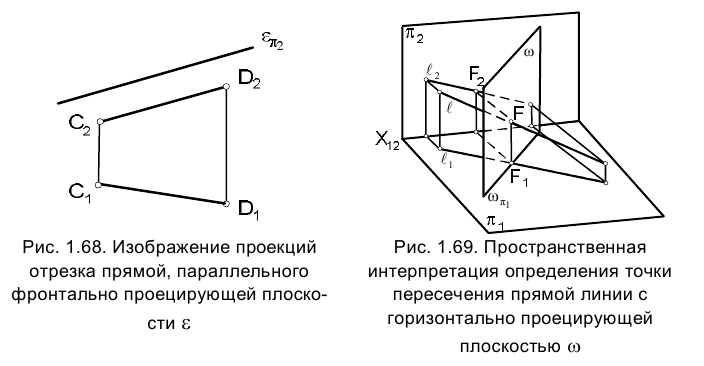
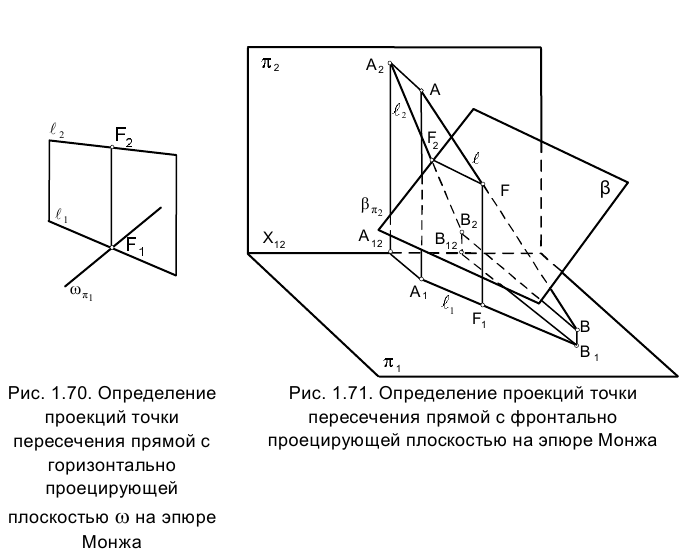
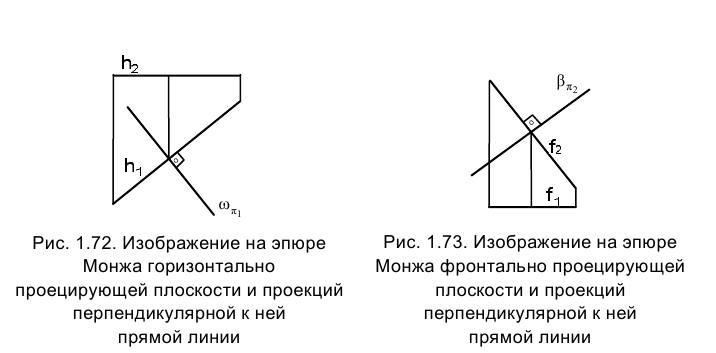
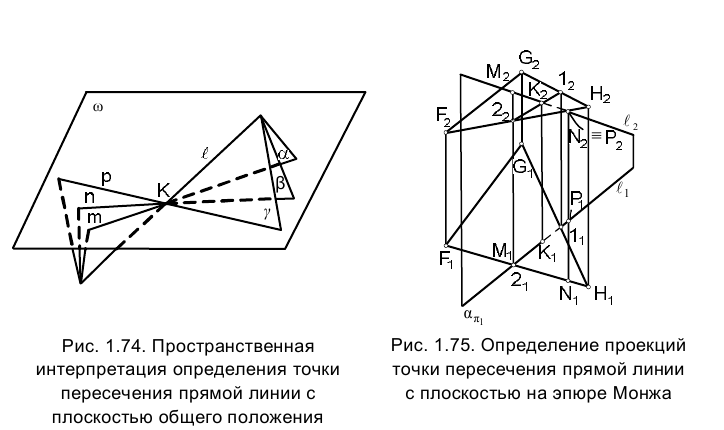
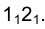
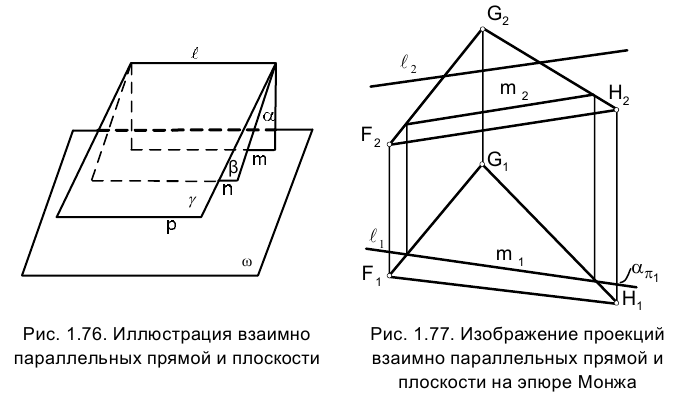
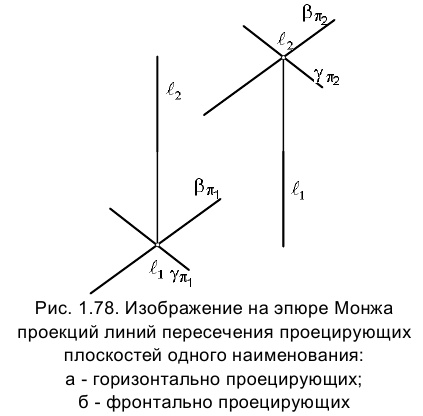
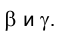
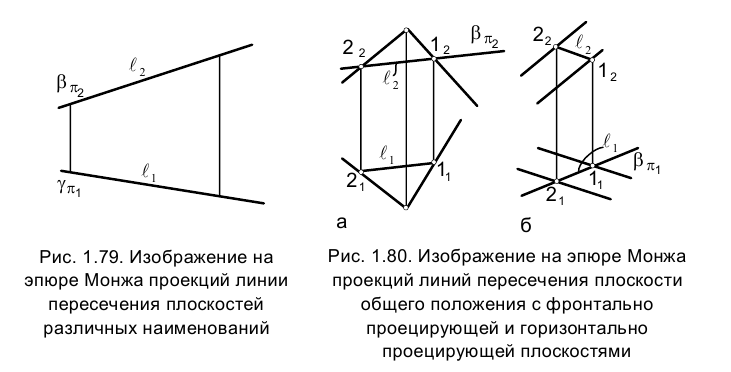
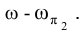
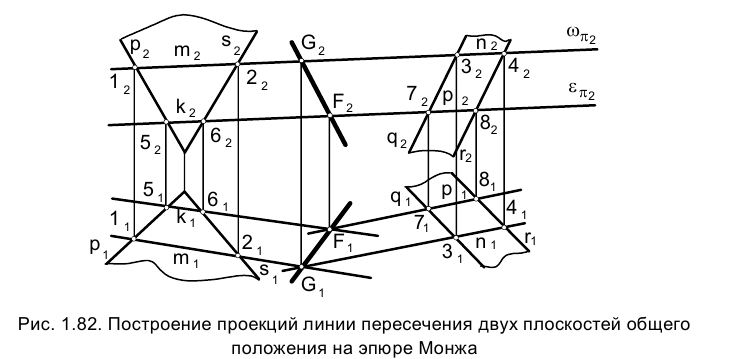
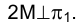
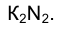
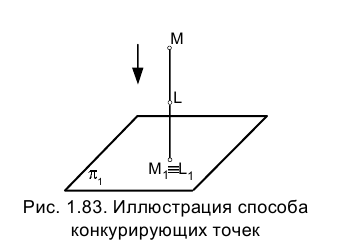
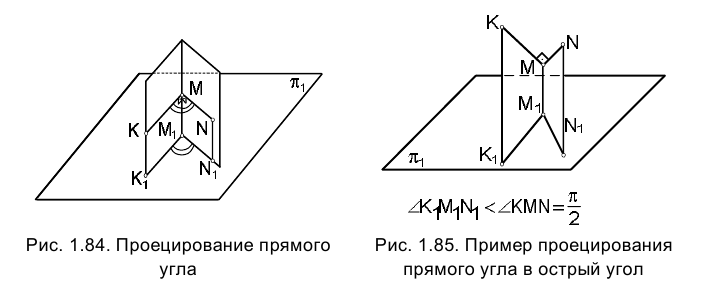
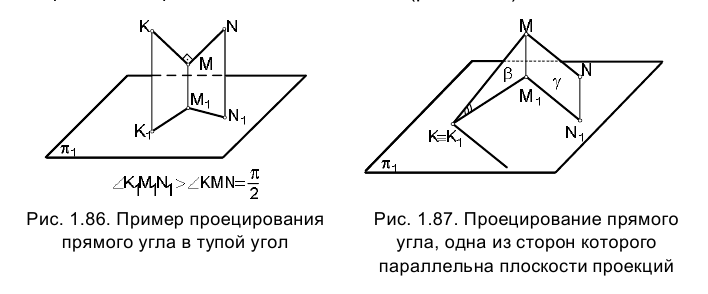
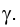
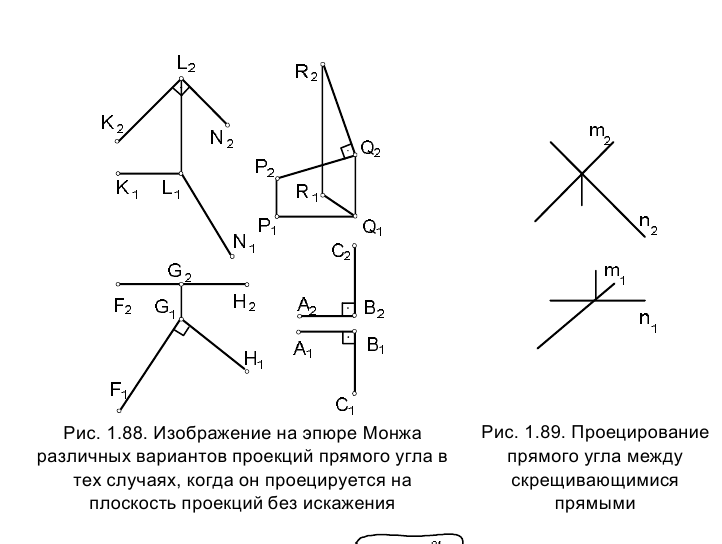
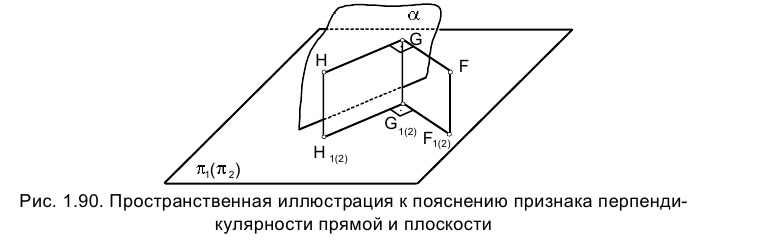
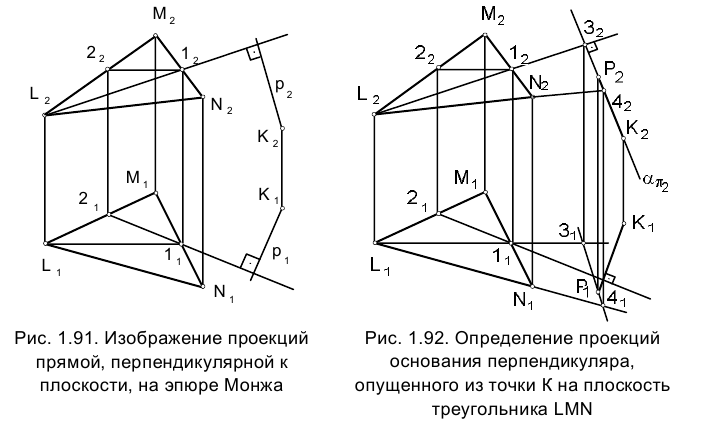
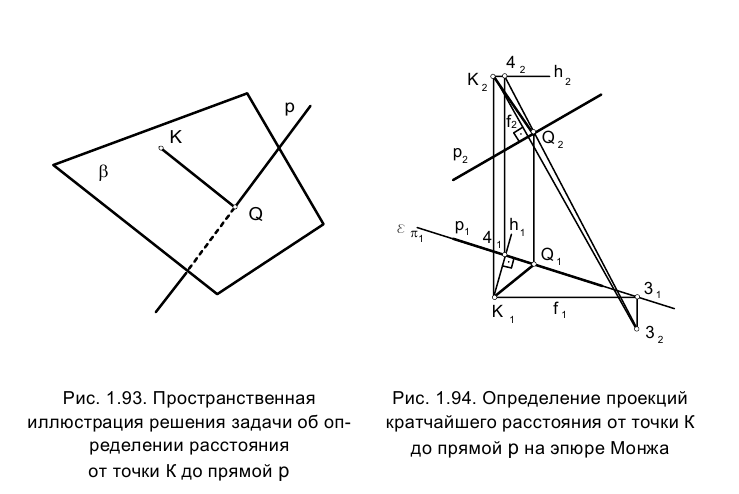
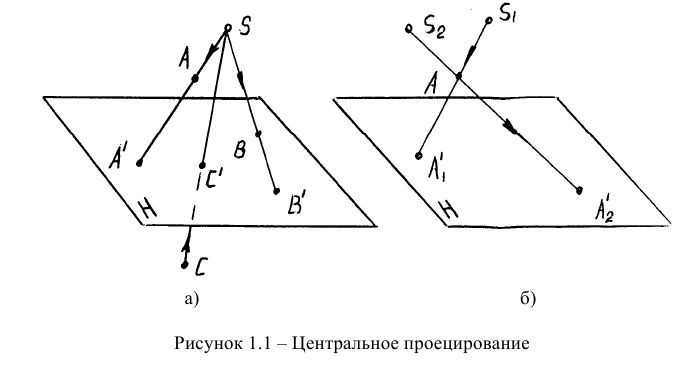
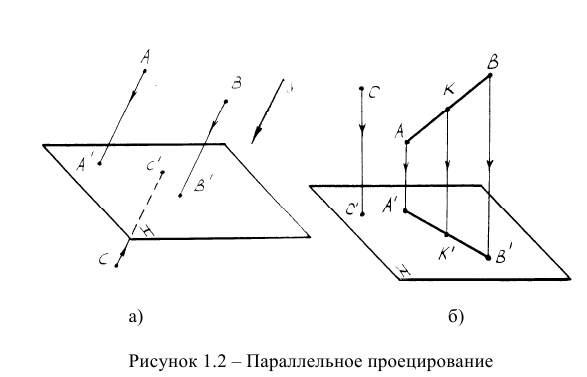

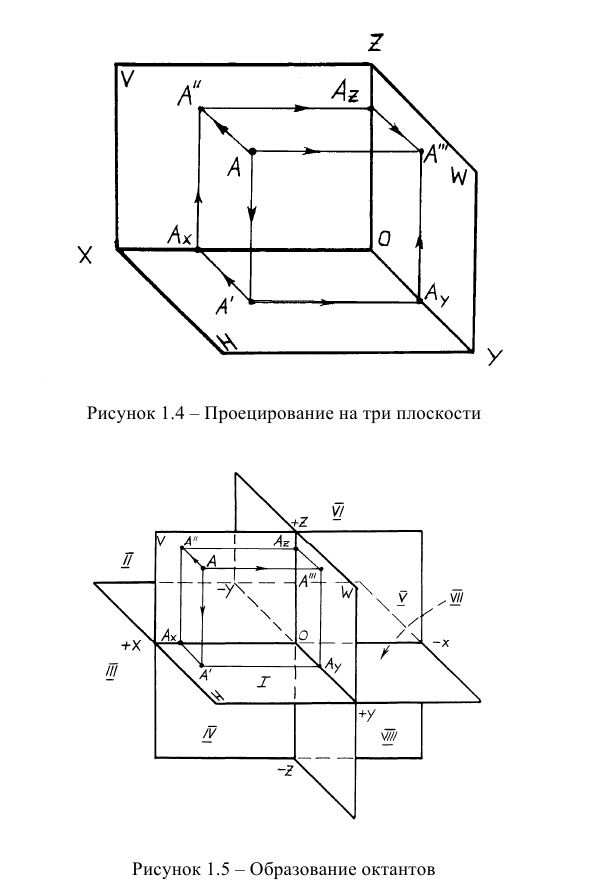
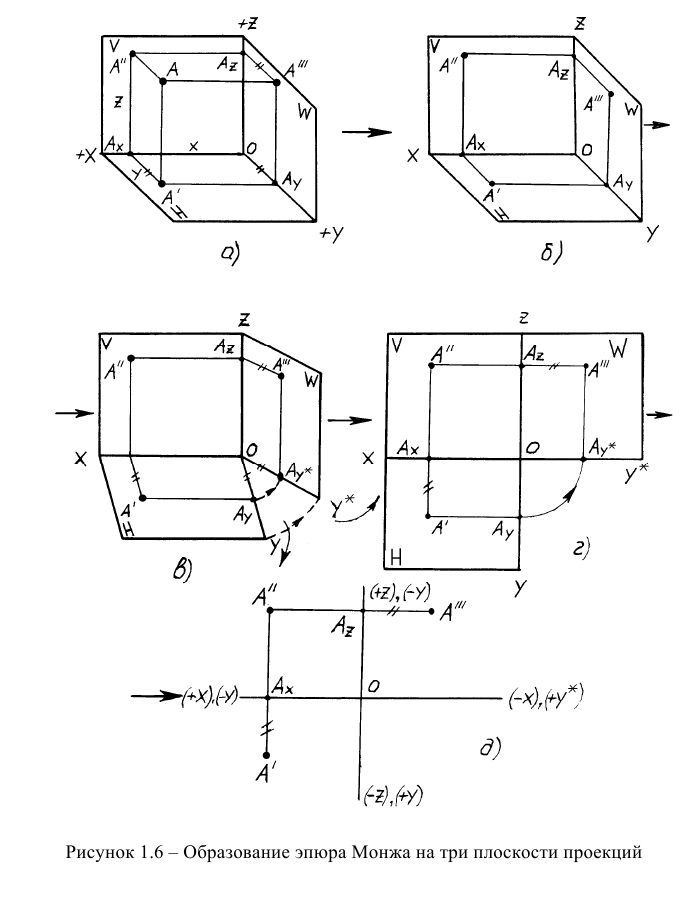
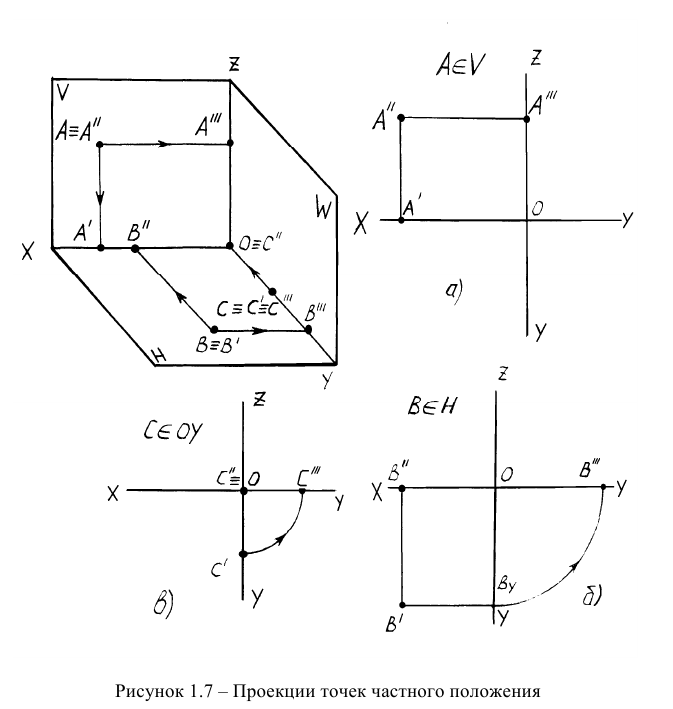
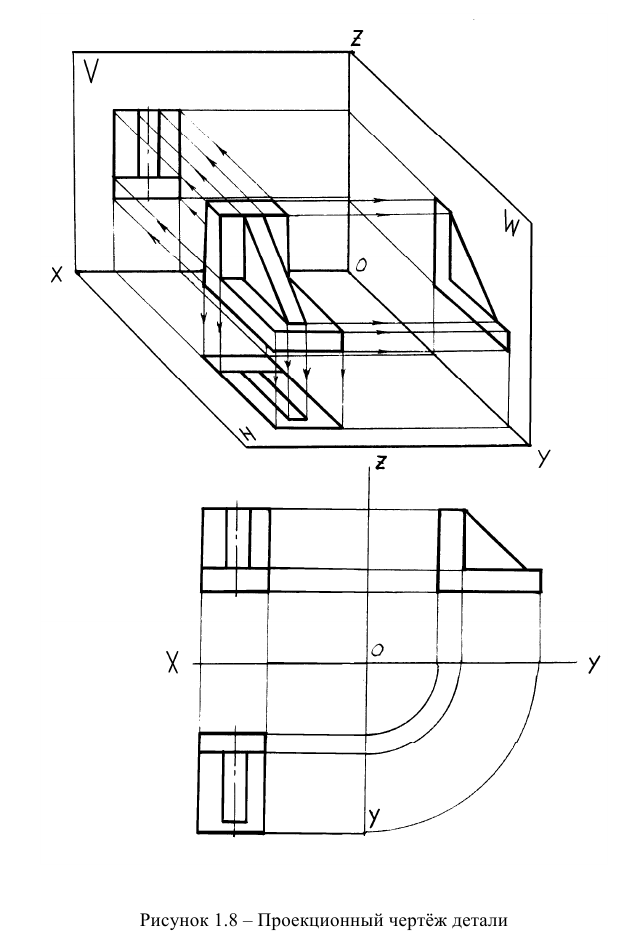
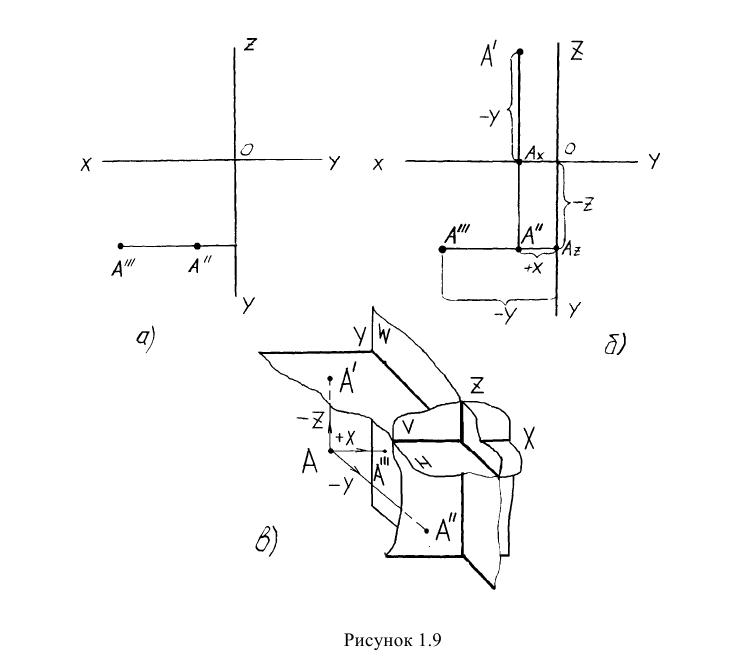
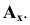
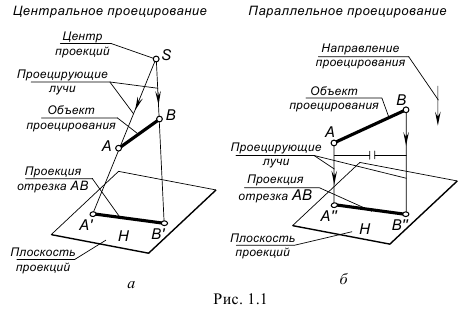
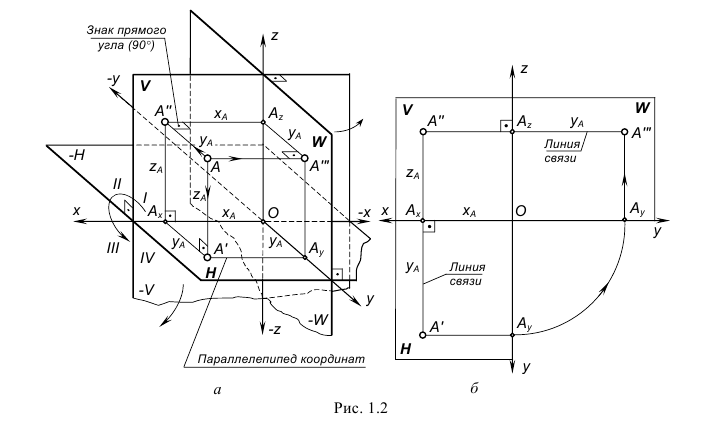
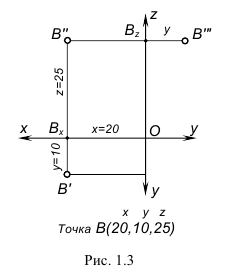
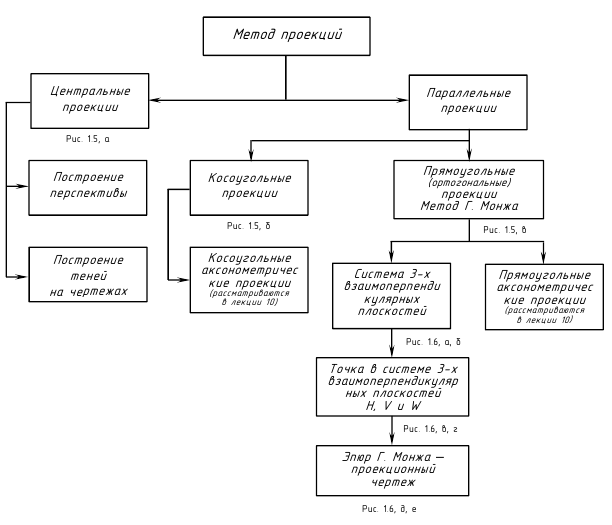
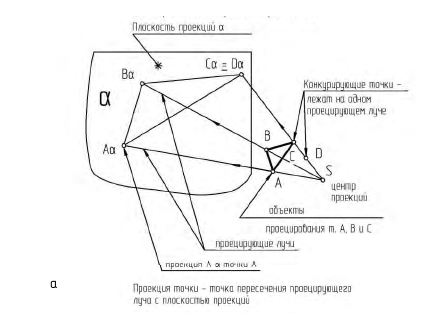
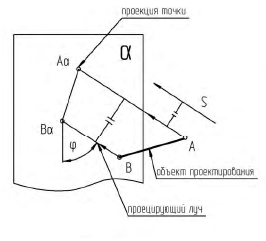
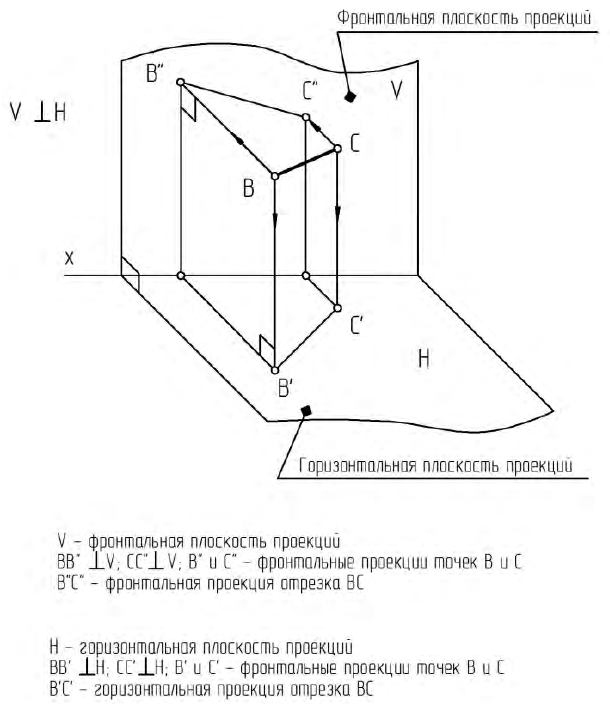
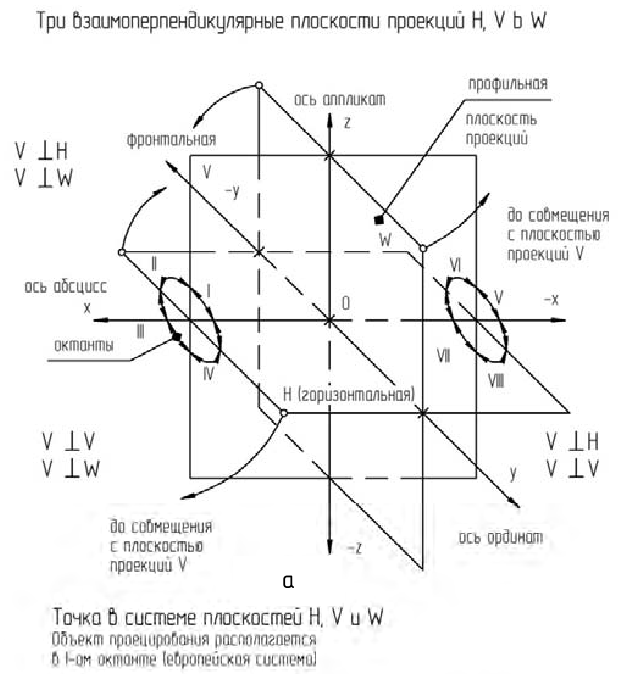
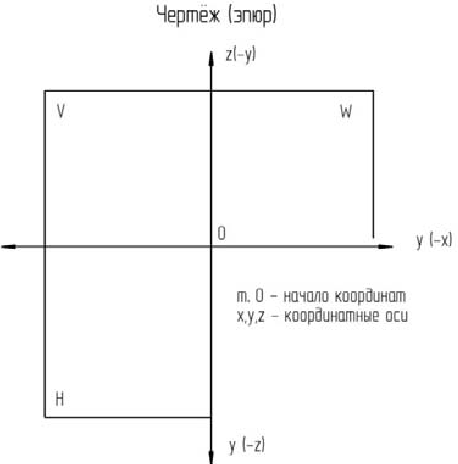
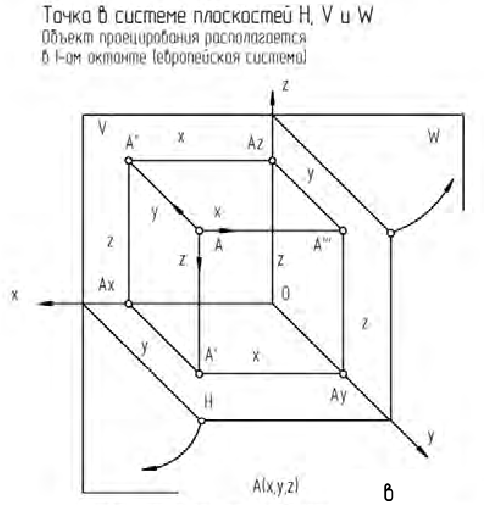
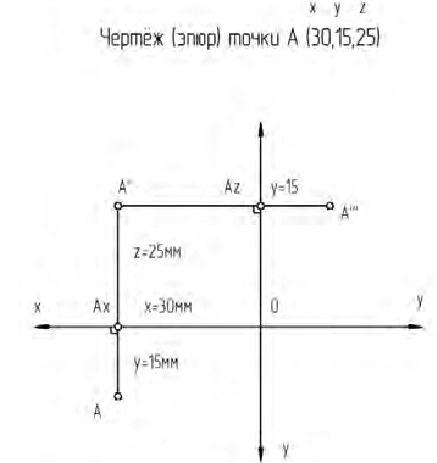
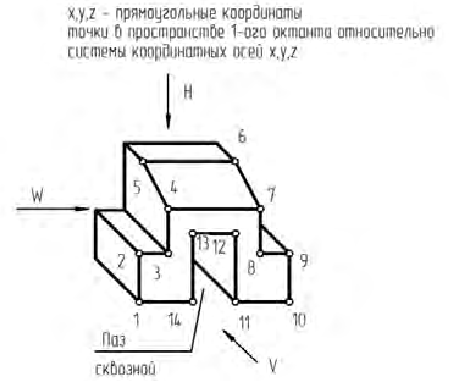
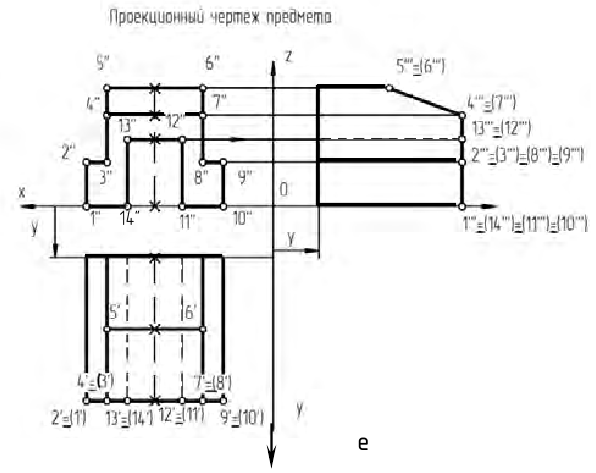
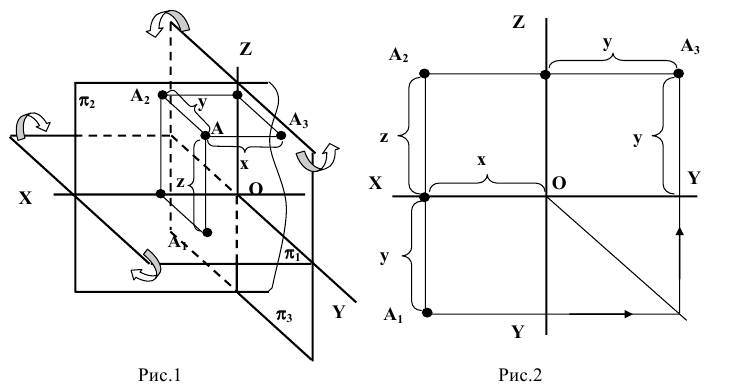
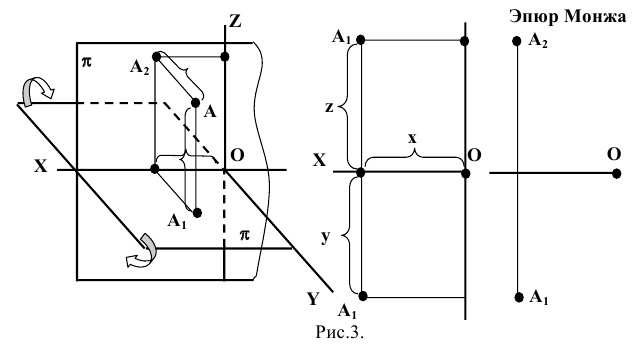
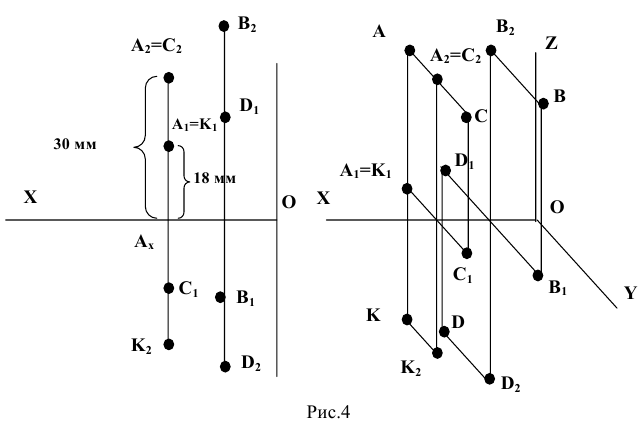
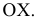
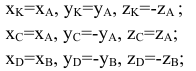
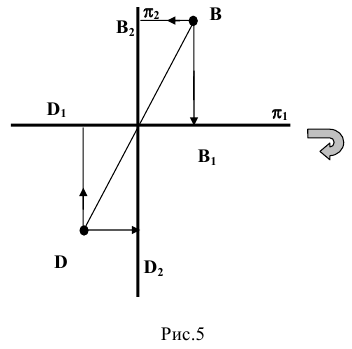
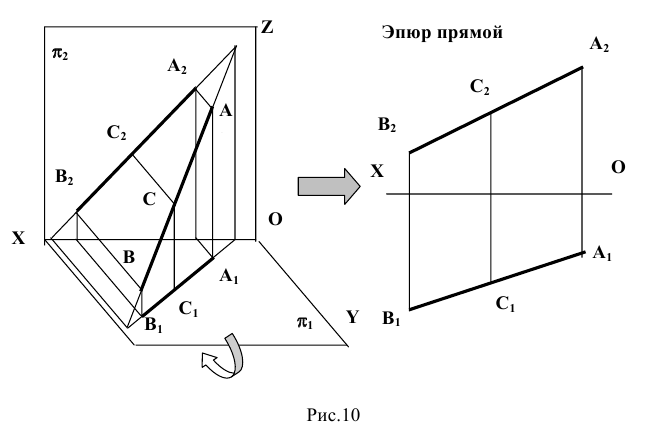
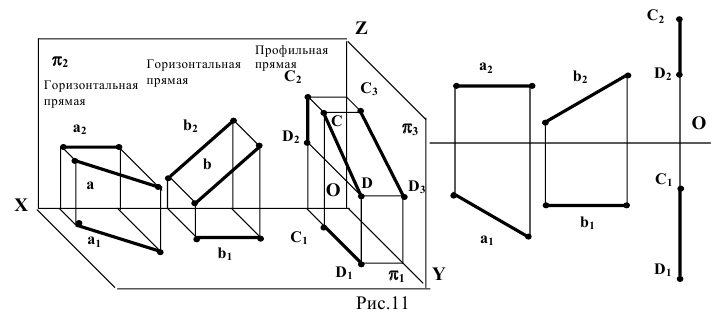
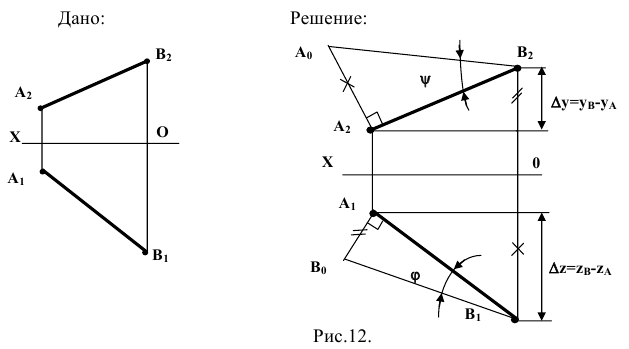
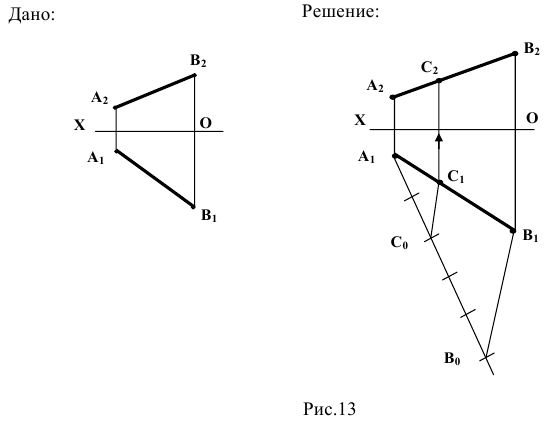
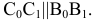
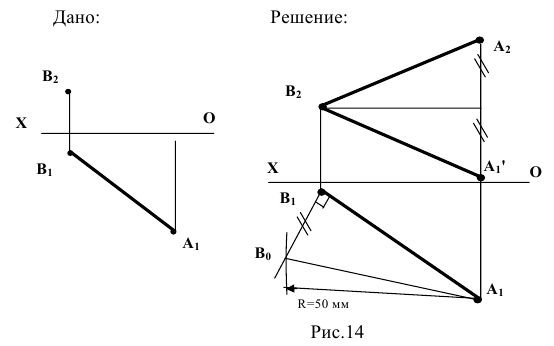
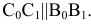
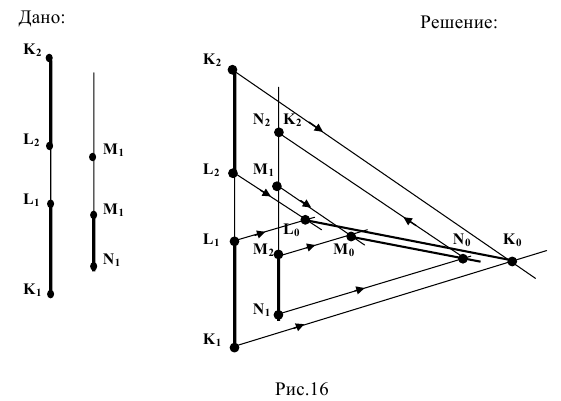
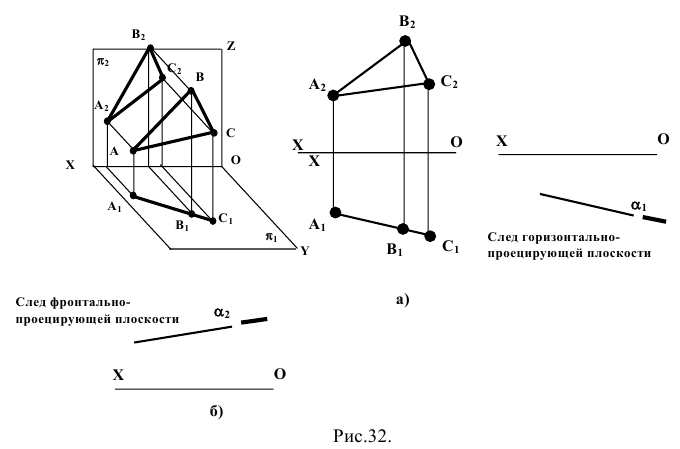
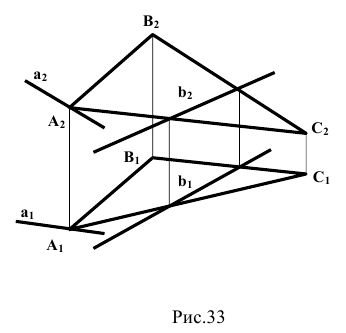
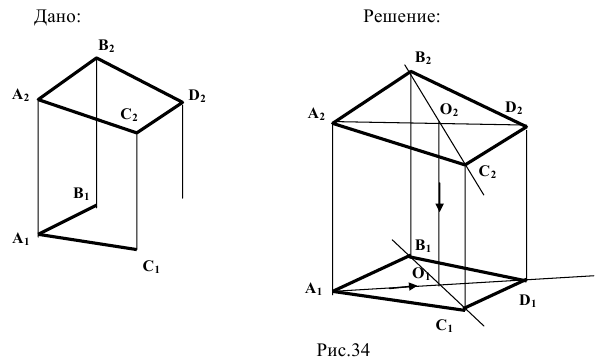
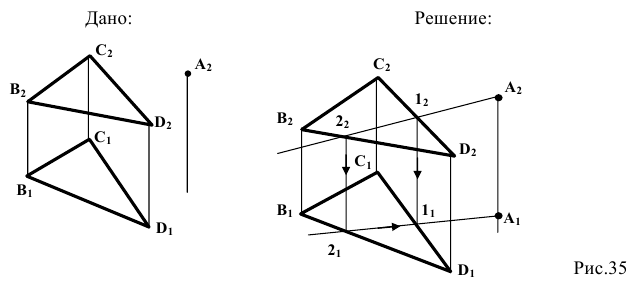
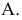
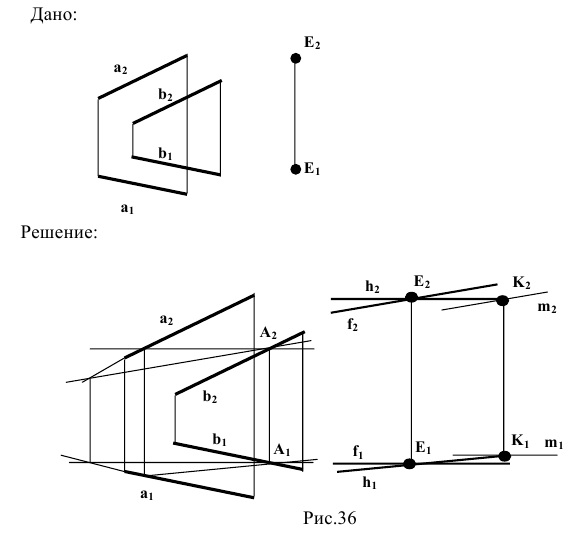
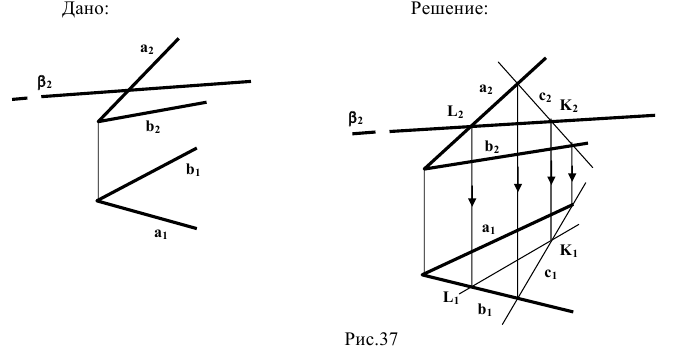
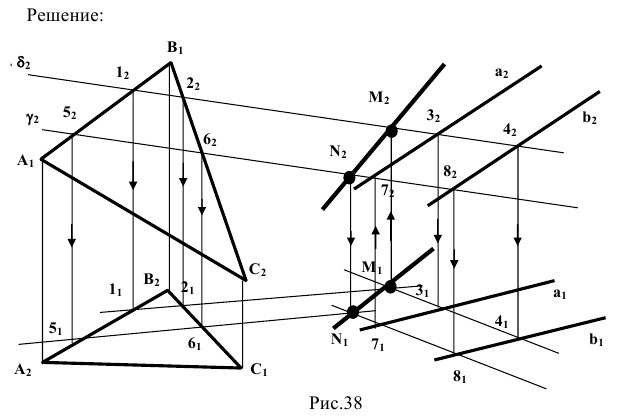
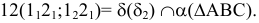
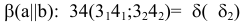
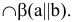
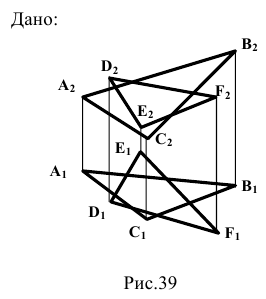
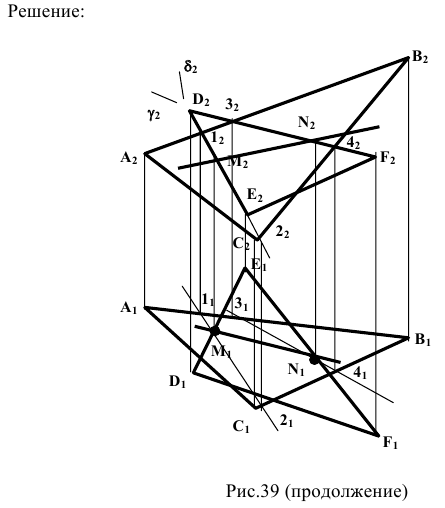
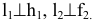
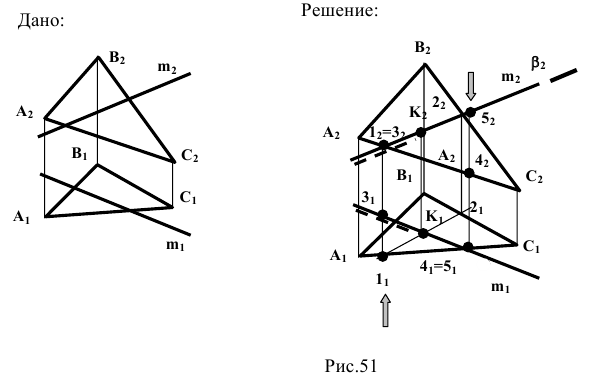
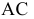
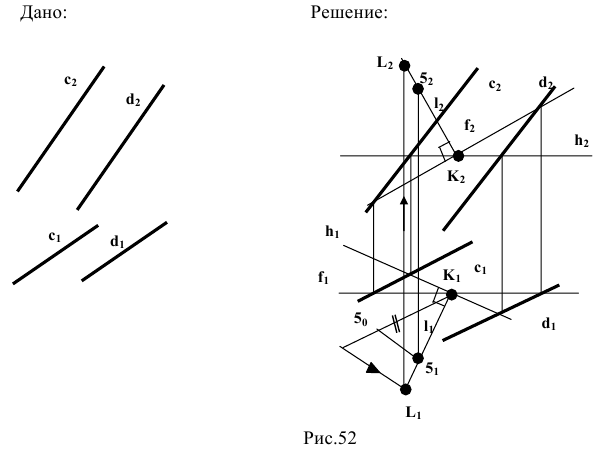
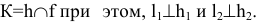
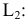
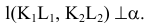
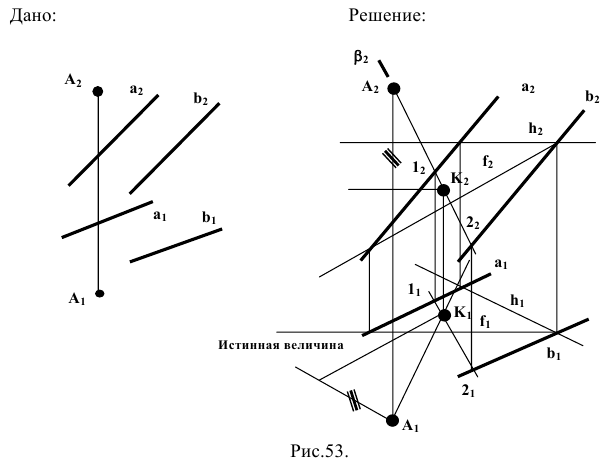
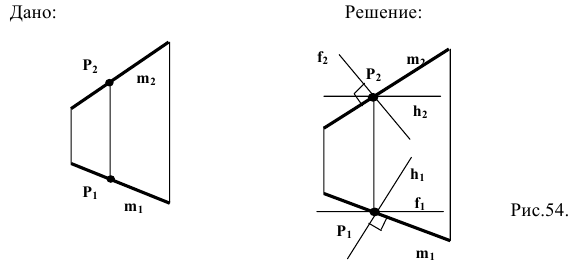
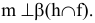
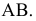
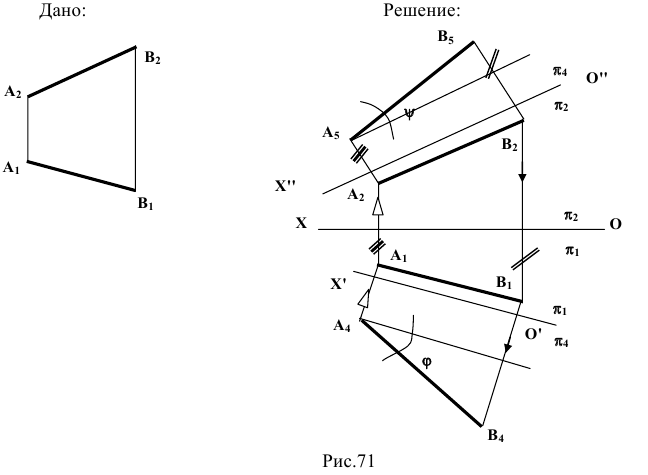
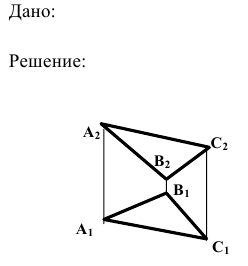
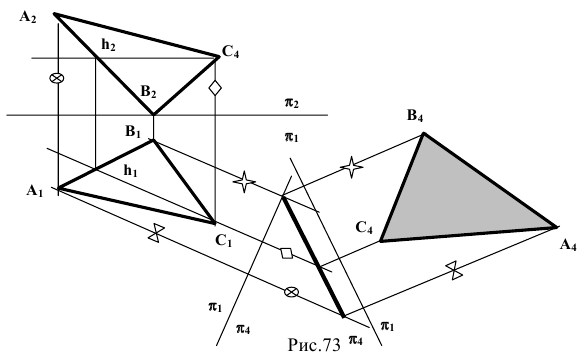
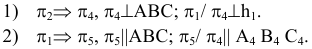
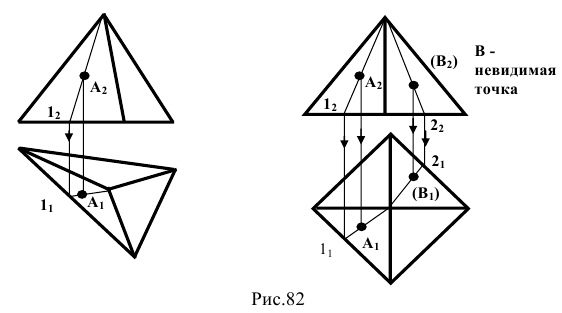
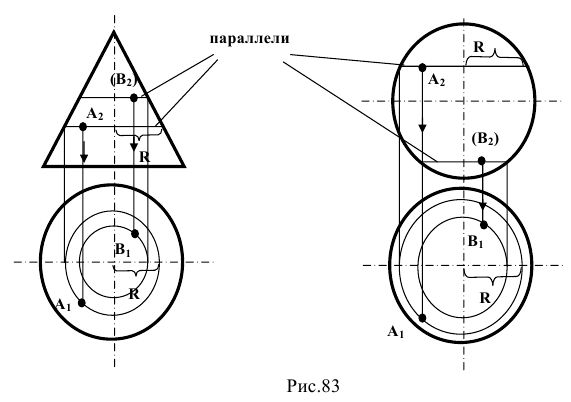
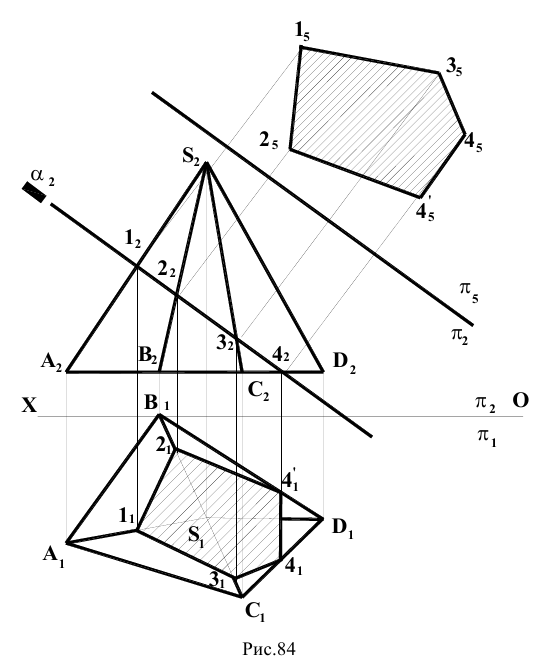
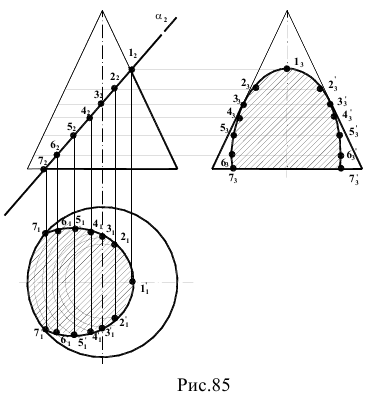
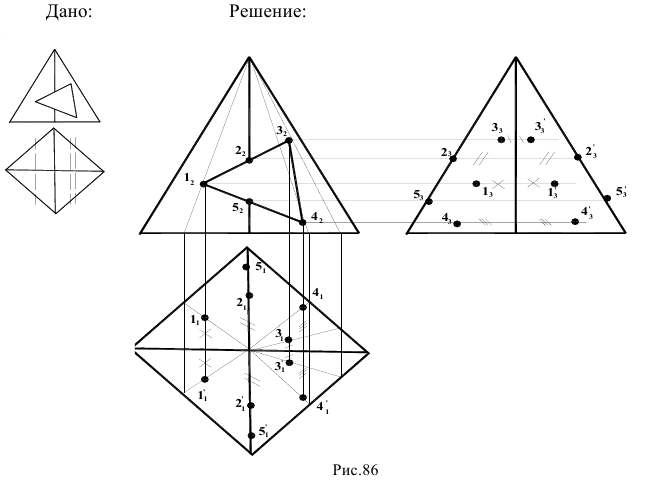
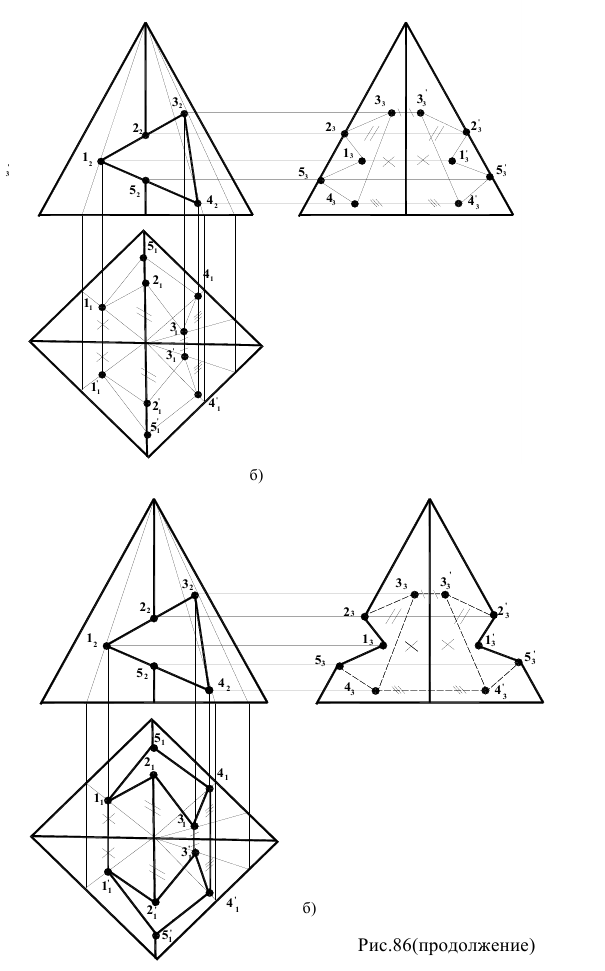
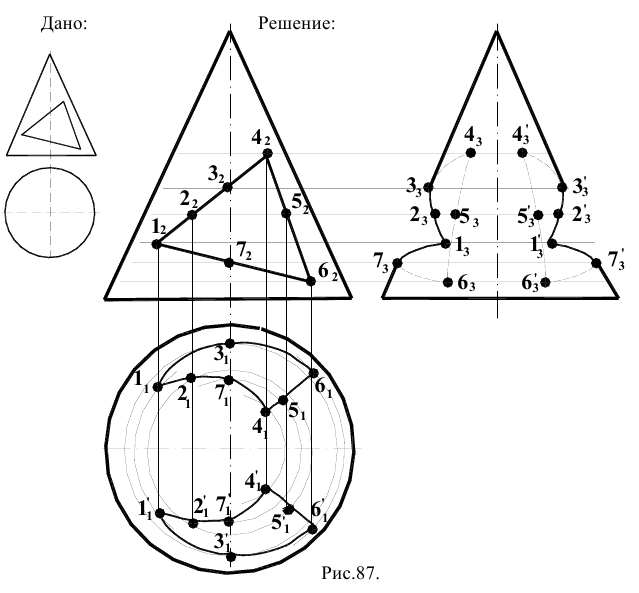
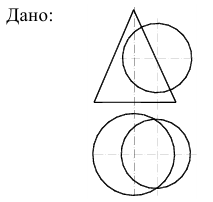
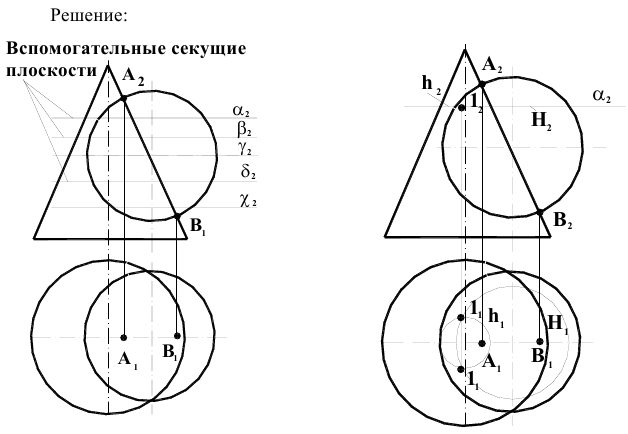
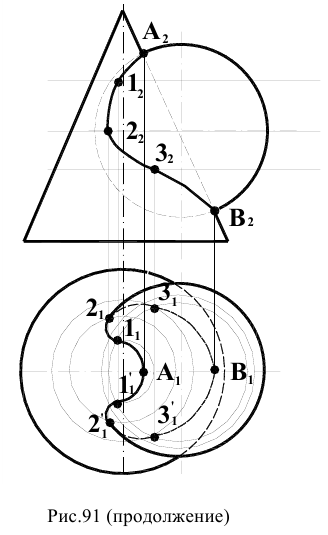
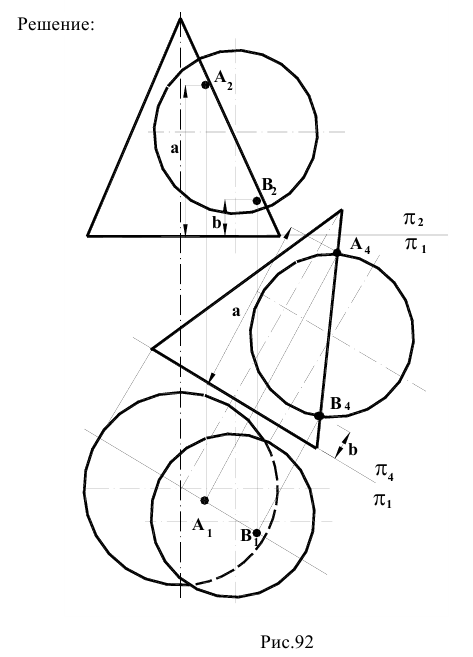
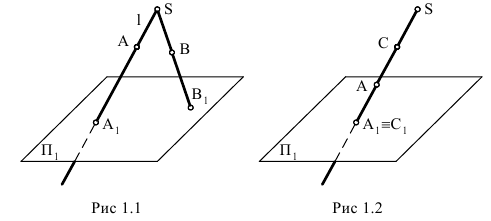
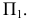
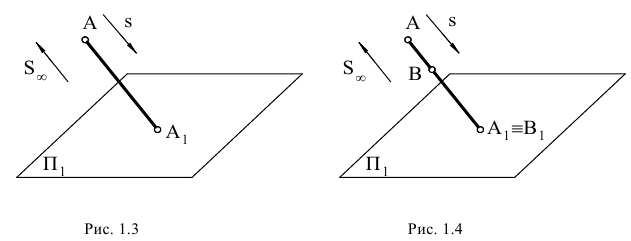
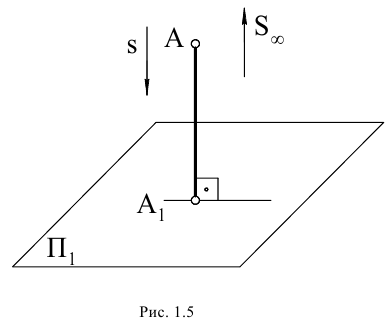
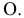
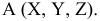
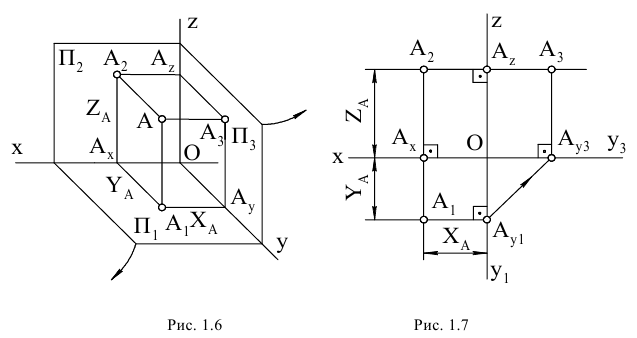
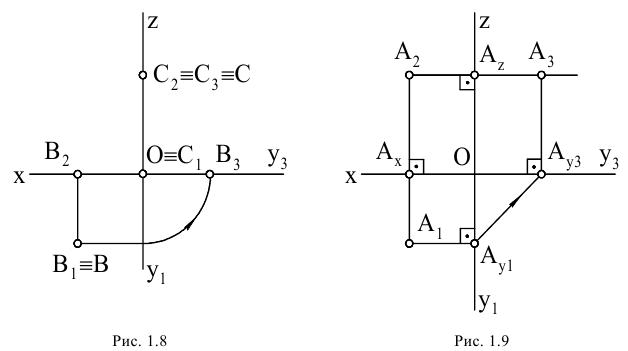
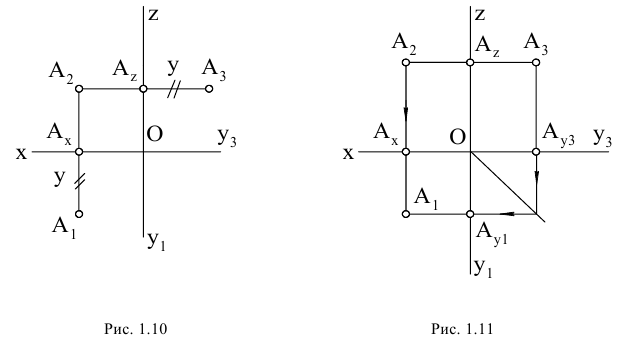
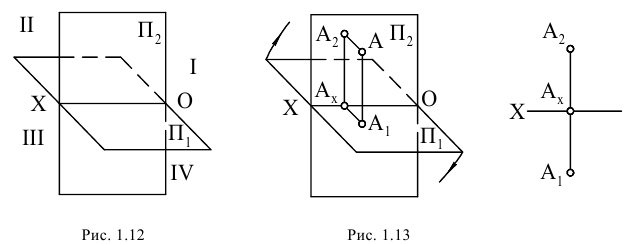
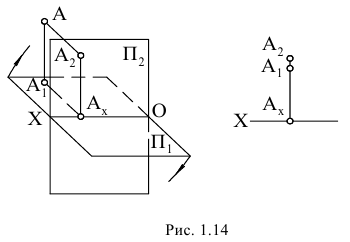
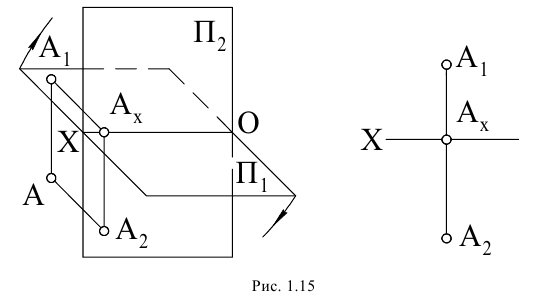
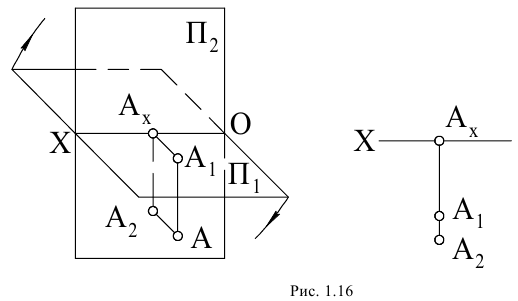
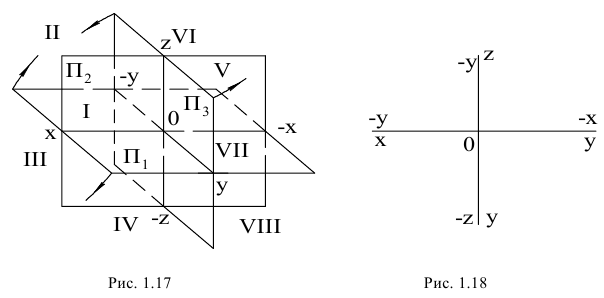

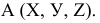
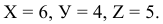
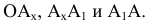
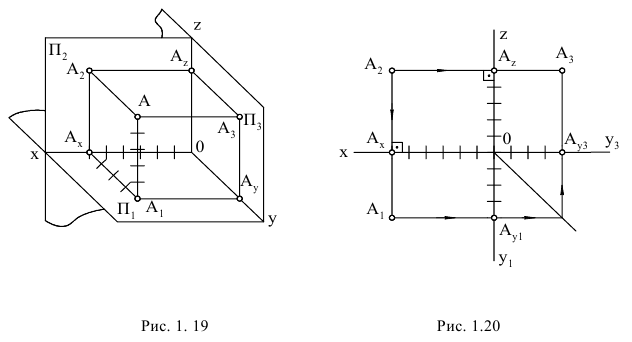
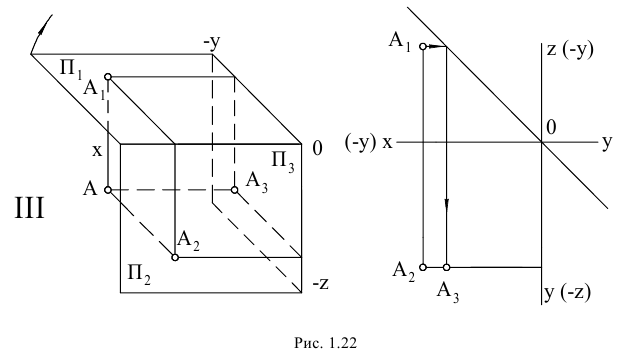
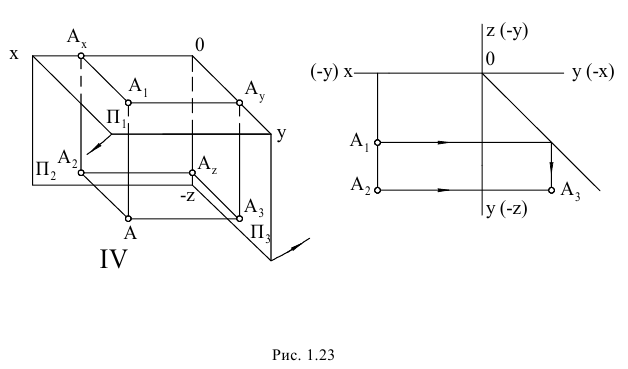
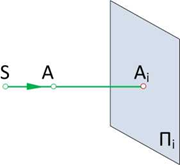
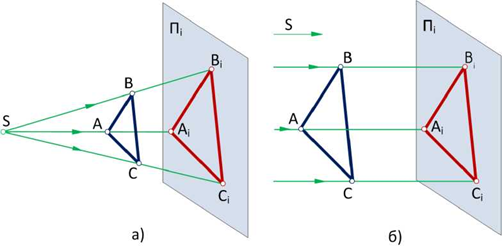
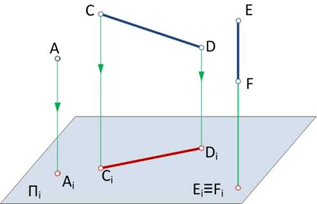
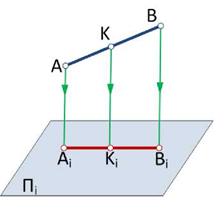
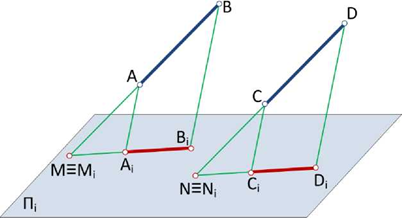
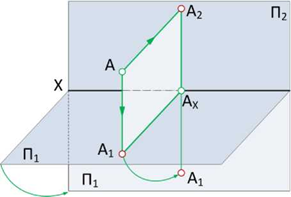
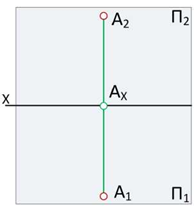

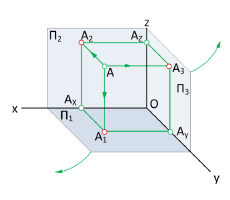
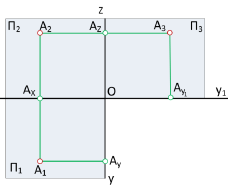
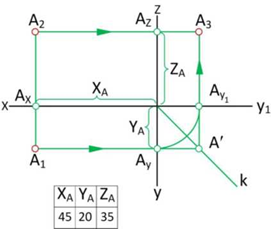
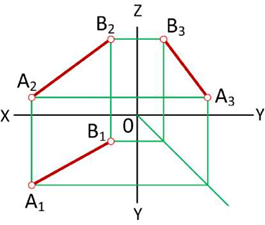
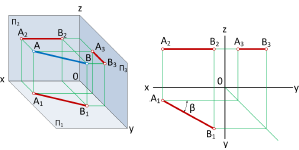
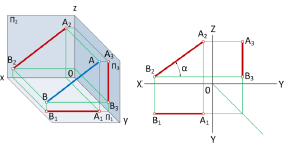
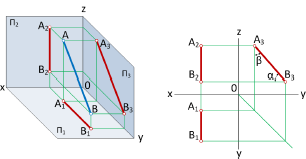
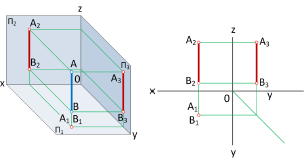
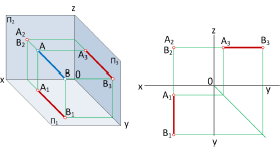
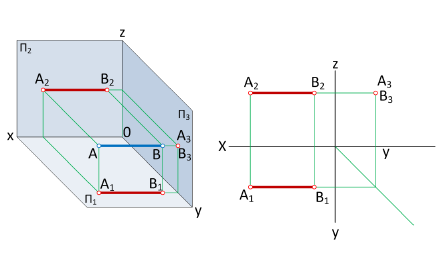
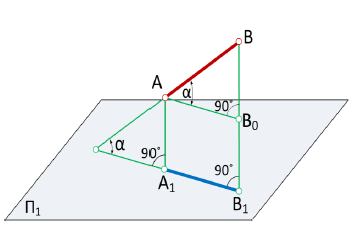
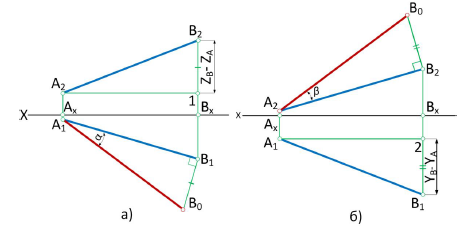
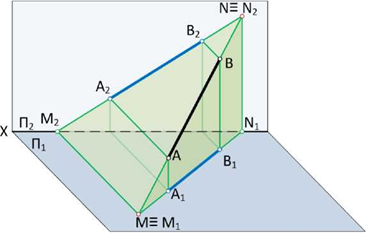
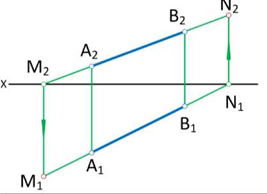
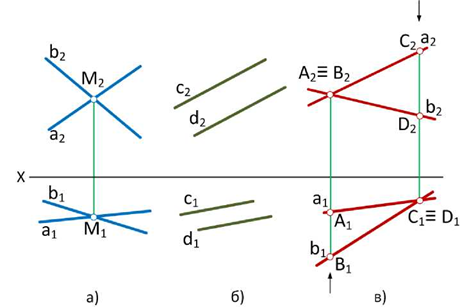
 a1 ∩ b1 = М1; а2 ∩ b2= М2; М1 M2
a1 ∩ b1 = М1; а2 ∩ b2= М2; М1 M2 x
x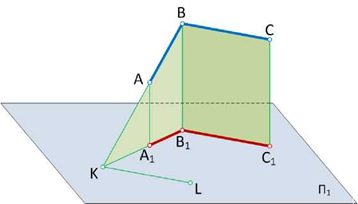 Рисунок 17.
Рисунок 17.