Что значит прочитайте график функции
Урок «Изучение графика числовых функций»
Краткое описание документа:
Каждый старший школьник должен уметь читать графики числовых функций. Такие навыки начинают отрабатываться с момента знакомства с графиками в курсе математики. К 10 классу эти умения должны получить достаточно устойчивый уровень. Хотя с самим понятием чтения графиков, в более глубоком смысле, обучающиеся знакомятся именно в 10 классе. И в помощь учителю, который собирается объяснять материал по данной теме, разработан данный видеоурок.
Здесь содержится полезная, полная и качественная информация, усвоение которой не затруднено ничем. Обучающиеся легко освоят материал по теме, так как он подобран в соответствии со рядом требований, в том числе по возрасту обучающихся.
Урок длится 5:32 минут. Практически столько же времени, если не отвлекаться на какие-то посторонние моменты, понадобится учителю, чтобы объяснить новый материал на уроке. Здесь же время строго регламентировано. Поэтому пока обучающиеся будут просматривать видеоурок, у них не будет времени отвлекаться, иначе они не поймут суть происходящего. Так с помощью данного урока можно сформировать у обучающихся такие качества, как внимательность, дисциплинированность и самостоятельность.
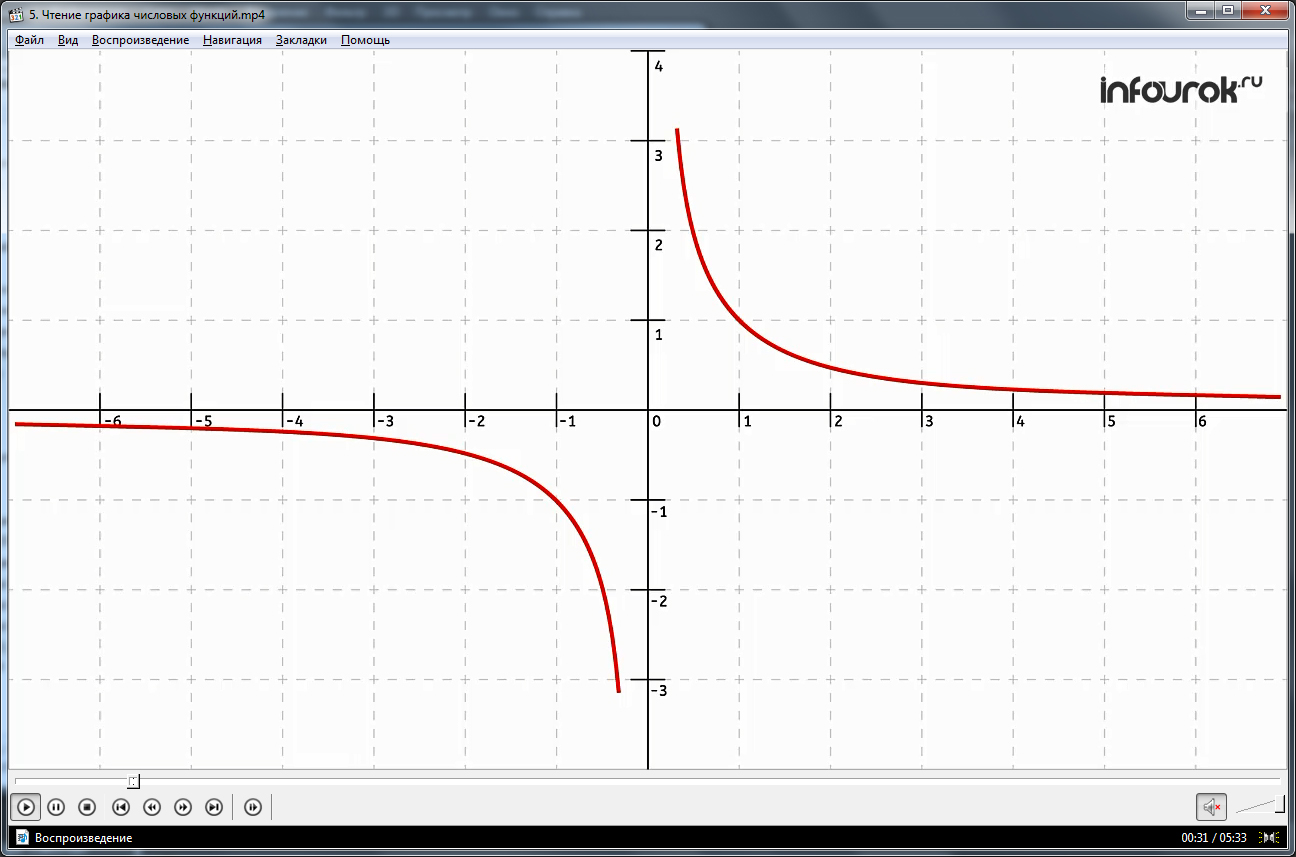
Автор урока обращает внимание слушателей на то, что чтение графиков числовых функций имеет широкое применение в нашей жизни. Особенно часто чтение графиков используется в экономике. При этом на экране изображен график некоторой функции.
Здесь же автор предлагает вспомнить, какая функция называется числовой. Пока обучающиеся начинают вспоминать, он напоминает им данное понятие. При этом объяснение сопровождается иллюстрацией. При этом, получается, что необходимо также вспомнить, что называется областью определения и областью значений функции. Автор напоминает и то, как выглядит уравнение функции в общем виде.
Чтобы обучающимся было проще понять принцип чтения графиков функций, необходимо вспомнить, что называется аргументом, то есть зависимой переменной, и независимой переменной. После этого предлагается рассмотреть некоторую произвольную функцию и построить ее график, подобрав пары чисел, которые являются координатами точек в системе координат. Когда график построен, вводится определение графика функции.
Далее автор говорит, что означает прочитать график функции. Получается, что для этого необходимо перечислить ее свойства, которые видны по графику. При этом перечисляются те свойства, которыми обладают все функции, и те, которыми обладают только некоторые функции.
Затем предлагается рассмотреть в качестве примеров, известные функции, которые были изучены в курсе алгебры ранее. Таких функций рассматривается две, последовательно. Сначала на экране изображается график функции, а затем подробно описывается каждое свойство, которым обладает функция. На каждом пункте автор останавливается и поясняет, что и как получается.
На этом видеоурок завершается, но не заканчивается занятие в школе. Поэтому оставшееся время желательно посвятить закреплению материала, подобрав для этого необходимые задания.
Урок будет полезен как для учителей, так и для обучающихся.
Чтение графика числовой функции.
Чтение графиков функций имеет большое практическое значение. В частности, использование функциональных зависимостей и построение графиков широко применяется в экономике.
Для изучения сегодняшней темы нам необходимо вспомнить: какая функция называется числовой?
Числовой функцией называется правило, с помощью которого каждому элементу из множества икс большое мы ставим в соответствие единственный элемент из множества игрек большое.
Множество Х называется областью определения функции.
Множество У называется множеством значений функции.
Равенство игрек равен эф от икс называется уравнением функции.
А что называется графиком функции?
Если дана функция игрек равно эф от х, где икс принадлежит икс большому и возьмем все пары икс, игрек и поставим им в соответствие соответствующие точки координатной плоскости, то получим график функции. График функции – это графической изображение зависимости между множествами икс большое и игрек большое.
1)область определения функции;
2)область значений функции;
3)нули функции – значения аргумента, при которых функция равна нулю;
4)промежутки знакопостоянства функции, т.е.промежутки,
где значения функции имеют один и тот же знак;
5)промежутки монотонности функции, т.е. промежутки, где функция возрастает или убывает;
6)наибольшееи наименьшее значения функции, т.е. самое большое и самое маленькое значение зависимого переменного;
Свойства, которые имеют не все функции:
9) четность, нечетность;
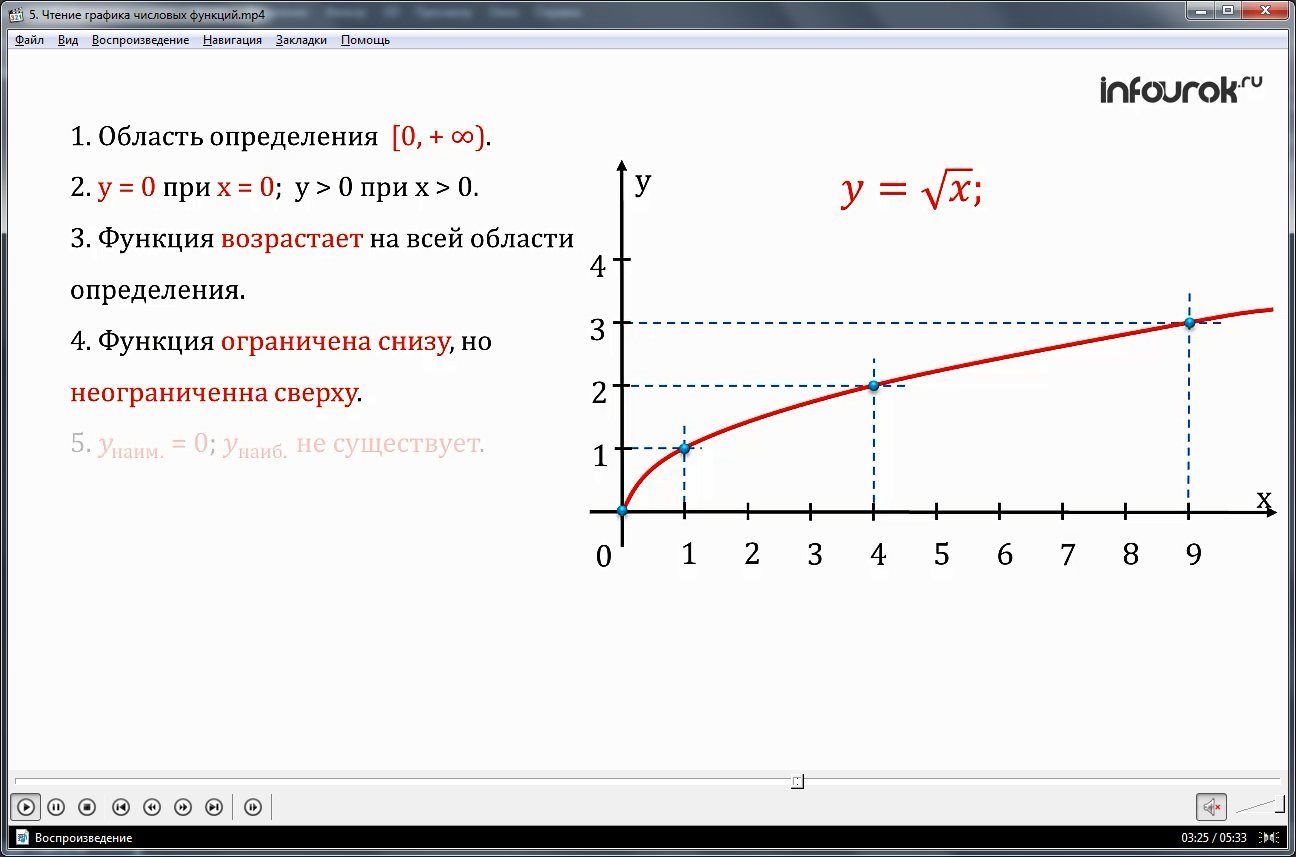
Прочитаем графики известных нам функций, например,игрек равен квадратный корень из икс.
1. Область определения функции —
луч от нуля до плюс бесконечности
2. Игрек равен нулю при икс равному нулю; игрек больше нуля при икс больше нуля.
3. Функция возрастает на всей области определения.
6.Функция непрерывна в заданной области определения.
7. Область значений функции — луч от нуля до плюс бесконечности
8.График обращен выпуклостью вверх.
у=кх+в
Прочитаем график ограниченной функции, график которой изображен
1.Область определения функции – отрезок от минус трех до трех.
7.Функция ограничена и сверху и снизу.
8.На отрезке минус трех до нуля функция выпукла вниз, а
на отрезке нуля до трех выпукла вверх.
9.Непрерывна на всей области определения.
Сегодня, мы научились читать графики элементарных функций. На следующем уроке мы продолжим чтение графиков тригонометрических функций, показательной, логарифмической.
Построение графиков функций
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
Ветви вниз, следовательно, a 0.
Координата вершины 
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:
Урок алгебры в 9 классе «Чтение свойств функции по графику»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Тема урока: Чтение свойств функции по графику
Базовый учебник: Ю.Н. Макарычев «Алгебра, 9», 2014 г.
Образовательные : систематизировать и обобщить знания о свойствах функций, развивать навыки построения и прочтения графиков функций;
Развивающие : развивать логическое мышление, умение делать обобщения и выводы;
Воспитательные : формирование умений работать в микро группах, способствовать воспитанию чувства успеха от интеллектуального труда.
Тип урока: урок обобщения и систематизации знаний.
Используемое оборудование: мультимедийный проектор, ноутбук.
Используемые технологии: системно – деятельностный подход, развивающее обучение.
Форма организации деятельности учащихся: групповая, индивидуальная, фронтальная.
Обобщение и систематизация знаний.
Закрепление полученных знаний
Контроль усвоения знаний, коррекция.
Современная математика их знает множество, и у каждой свой неповторимый облик, как неповторим облик каждого из миллиардов людей, живущих на земле.
Её облик можно представить сложенным из набора характерных свойств.
О каком математическом понятии идет речь? (о функции)
А что же такое функция? (ученики дают определение).
Сформулируйте цель урока.
Эпиграфом к уроку возьмем слова:
Величие человека – мыслить.
Учащиеся в тетрадях записывают тему урока « Чтение свойств функции по графику ».
II. Актуализация знаний.
В течение 1 минуты посовещайтесь в парах и вспомните свойства функций. Затем каждая пара называет по 1 свойству.
Наибольшее и наименьшее значения функции
Какому свойству отведем центральное место? (область определения)
Дайте определения следующим понятиям:
1)область определения функции;
2) множество значений функции;
3)возрастание и убывание функции.
Остальные свойства функций мы вспомним с вами в ходе выполнения заданий в течение урока.
Обобщение и систематизация знаний.
№ 1. Прочитать свойства функции по графику.
Область определения функции : D ( y )=(-10;2)
Область значений функции: E ( y )=[-2,5;5]
Функция возрастает х € [-7;-4] ᴗ [-0,5;1]; убывает х € [-10;-7] ᴗ [-4;-0,5] ᴗ [1;2)
Функция принимает положительные значения х € (-10;-9) ᴗ (-5;-2)
Функция принимает отрицательные значения значения х € (-9;-5) ᴗ (-2;2)
Функция не является ни четной, ни нечетной
4 . Закрепление полученных знаний
По графику указать:
1)Область определения (-5;5)
2)наибольшее значение функции: 5
3)Наименьшее значение функции:-2,8
4)Количество промежутков, на которых функция принимает отрицательные значения: 2
5)Количество нулей функции :3
Контроль усвоения знаний, коррекция.
Самостоятельная работа ( по вариантам )
1)Указать свойства функции по графикам
Сегодня на уроке мы систематизировали наши знания о функциях, их свойствах и графиках. Повторили алгоритм исследования и чтения графика функции.
Какие науки помогали нам повторить материал?
Геометрия (через любые две точки можно провести…)
Математика (если х = …, то у = …)
Алгебра (у = kx + b, y = …)
Чтобы упрочить ваши знания,
даю домашнее задание.
7. Домашнее задание
на открытый урок в 9 «А» классе
по теме «Чтение свойств функции по графику», проведенный
Чуркиной Аленой Сергеевной.
Чуркина Алена Сергеевна проводила открытый урок в 9 классе 12.09.16 г. по теме: « Чтение свойств функции по графику ».
Урок прошел на высоком методическом уровне. Цели были определены и доступны для учащихсяВсе этапы урока последовательны и логически связаны. Структура урока соответствует данному типу урока. Обеспечивалась целостность и завершенность урока. Соблюдался принцип систематичности и последовательности формирования знаний, умений, навыков. Использование на уроке наглядного материала способствовало развитию обучения, сознательности и активности учащихся, их познавательной деятельности, раскрытию связи теории с практикой.
В течение урока были использованы следующие методы обучения: диалог учитель-ученик, актуализация ранее изученного материала, самостоятельная работа. Эти методы обучения обеспечивали поисковый и творческий характер познавательной деятельности учащихся.
На каждом этапе осуществлялась постановка учебных задач, сочетались разные формы работы на уроке: индивидуальная, групповая, парная. Осуществлялся контроль учителя, самоконтроль и самооценка результатов работы. Были подведены итоги урока. Осуществлялось чередование разных видов деятельности обучающихся.
Урок был организован с использованием информационно-коммуникативных технологий обучения. Был правильно определен объем учебного материала на уроке, умелое распределение времени, характер обучения был демократичным, объективным. На уроке царила доброжелательная атмосфера, и учащиеся чувствовали себя достаточно свободно.
Речь учителя была грамотной, доступной, содержательной.
Учащиеся были активны и организованны на разных этапах урока, были доброжелательны к учителю, показали умения творческого применения знаний, умений и навыков самостоятельно делать выводы.
Учитель математики Н.Н. Устинская
на открытый урок в 9 «А» классе
по теме «Чтение свойств функции по графику», проведенный
Чуркиной Аленой Сергеевной.
Дата проведения: 12.09.2016г. Класс: 9А
Тип урока: первичное формирование умений и навыков.
Цель посещения: знакомство с опытом работы учителя.
Триединая дидактическая цель:
1. систематизировать и обобщить знания о свойствах функций, развивать навыки построения и прочтения графиков функций;
2. развивать логическое мышление, умение делать обобщения и выводы;
3. формирование умений работать в микро группах, способствовать воспитанию чувства успеха от интеллектуального труда.
Класс и оборудование ( раздаточный материал) полностью готовы к уроку. Проверена подготовка учащихся к уроку, организовано внимание.
Создана атмосфера значительности, серьезности и важности работы учащихся.
Учитель четко и однозначно определил цель урока, чему должны научиться ученики в ходе урока, какими знаниями, умениями и навыками овладеть.
На этапе усвоения новых знаний, умений и навыков учащиеся правильно отвечали на вопросы. Класс активно выполнял все задания.
Самостоятельная работа учащихся сочеталась с объяснением учителя. Применялись различные способы активизации мыслительной деятельности: анализ, синтез, сравнение и сопоставление. Организовано осмысление, первичное обобщение и систематизация вновь сообщаемых знаний.
В ходе проверки понимания учащимися нового материала учитель добился устранения пробелов в понимании учащимися нового материала, выявил уровень глубины его осмысления.
Задавались вопросы, требующие мыслительной активности, самостоятельной мыслительной деятельности
На уроке для закрепления нового материала проведена самостоятельная работа, в ходе которой проверялось умение воспроизводить основные идеи нового материала. На этом этапе в памяти учащихся закреплены знания и умения, которые необходимы им для самостоятельной работы по новому материалу.
Учитель подвёл итоги урока: как работал класс, кто из учащихся работал особенно старательно, что нового узнали; дал короткие методические указания учащимся как они должны готовить домашнее задание.
Время урока было рационально распределено на этапы, и четко прослеживалась связь между ними. Учитель играл на уроке направляющую роль.
Работоспособность учащихся обеспечивалась за счет высокого темпа и четко поставленных целей.
Урок прошел плодотворно. Цель достигнута, задачи, поставленные на уроке, удалось решить на оптимальном уровне.