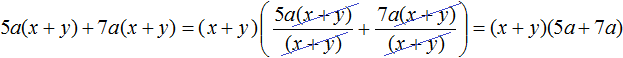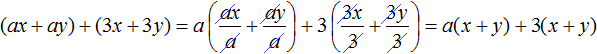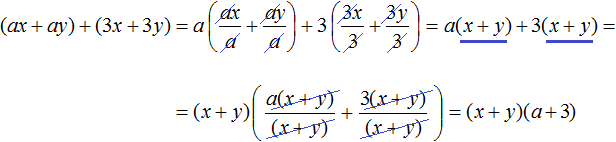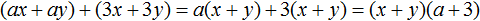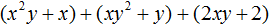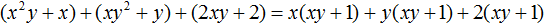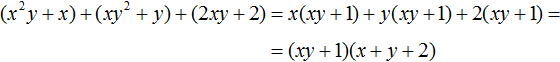Что значит представить в виде произведения многочленов выражение
Что значит представить в виде произведения многочленов выражение
Ключевые слова конспекта: произведение многочленов, умножение одночлена на многочлен, умножение многочлена на многочлен.
1. Умножение одночлена на многочлен
Пусть требуется умножить одночлен 2а 3 на многочлен 3а 4 – 4а 2 + а.
Составим произведение 2а 3 (3а 4 – 4а 2 + а).
При умножении одночлена на многочлен пользуются следующим правилом:
Распределительный закон умножения относительно сложения, на котором основано правило умножения одночлена на многочлен, древнегреческий математик Евклид в III в. до н.э. доказывал на языке «геометрической алгебры»: если одна из сторон прямоугольника является суммой нескольких отрезков, то площадь всего прямоугольника можно найти как сумму площадей его частей. Например, если а = а 1 + а 2 + а 3 – одна сторона прямоугольника, b – его вторая сторона, то площадь прямоугольника равна ab = (ах + а 2 + а 3 )b = ах 6 + а 2 b + а 3 b. Если считать а = а 1 + а 2 + а 3 многочленом, а b – одночленом, то мы получим правило умножения многочлена на одночлен.
В рассмотренном примере мы представили произведение одночлена и многочлена в виде многочлена. Вообще произведение одночлена и многочлена всегда можно представить в виде многочлена. Причём степень произведения будет равна сумме степеней одночлена и данного многочлена.
Пример 1. Умножим одночлен –3ху на многочлен 2х 2 у + 4ху 2 – 1.
Имеем:
–3ху • (2х 2 у + 4ху 2 – 1) = –3ху • 2х 2 у + (–3ху) • 4ху 2 + (–3ху) • (–1) = –6х 3 у 2 – 12х 2 у 3 + 3ху.
Запись можно вести короче, не выписывая промежуточные результаты:
–3ху • (2х 2 у + 4ху 2 – 1) = –6х 3 у 2 – 12х 2 у 3 + 3ху.
Каждое из произведений преобразуем в многочлен и сложим полученные многочлены:
4а(2а + 5) + 2а(3а – 1) – 1,5а(2а – 4) = 8а 2 + 20а + 6а 2 – 2а – 3а 2 + 6а = 11а 2 + 24а.
2. Умножение многочлена на многочлен
Пусть требуется умножить многочлен а + b на многочлен с + d. Составим произведение этих многочленов:
(а + b)(c + d).
Обозначим двучлен а + b буквой х и воспользуемся правилом умножения одночлена на многочлен:
(а + b)(с + d) = х(с + d) = хс + xd.
В выражение хс + xd подставим вместо х многочлен а + b и снова воспользуемся правилом умножения одночлена на многочлен:
хс + xd = (а + b)c + (а + b)d = ас + bc + ad + bd.
Итак,
(а + b)(c + d) = ас + bc + ad + bd.
Этот же результат для положительных а, b, с, d можно увидеть на рисунке, интерпретируя, вслед за Евклидом, произведение двучленов как площадь прямоугольника.
Произведение (а + b)(с + d) мы представили в виде многочлена ас + bc + ad + bd. Этот многочлен является суммой всех одночленов, которые получаются при умножении каждого члена многочлена а + b на каждый член многочлена с + d.
Мы пришли к следующему правилу:
При умножении многочлена а + b на многочлен с + d мы снова получили многочлен. Вообще произведение двух любых многочленов можно представить в виде многочлена. При этом если многочлен, содержащий m членов, умножается на многочлен, содержащий n членов, то в произведении получается многочлен, состоящий из mn членов (до приведения подобных членов). Этим удобно пользоваться для самоконтроля.
Пример 1. Умножим 3а 2 – 4аb + b 2 на многочлен 2а – b.
Умножение многочленов можно выполнять в столбик.
Из приведённого примера можно сделать полезный вывод: степень произведения многочленов равна сумме степеней многочленов–множителей. Действительно, первый множитель – многочлен степени 2, второй – двучлен степени 1, а их произведение – многочлен степени 2 + 1 = 3.
Рассмотрим пример умножения двух многочленов с одной переменной.
Пример 2. Представим в виде многочлена стандартного вида произведение многочленов 2x 2 – 3х + 1 и 5x + 4.
(2х 2 – 3х + 1)(5х + 4) = 10х 3 + 8х 2 – 15х 2 – 12х + 5х + 4 = 10х 3 – 7х 2 – 7х + 4.
Старшие коэффициенты многочленов–множителей равны 2 и 5, а старший коэффициент произведения равен 10. Свободные члены многочленов–множителей равны 1 и 4, а свободный член произведения многочленов равен 4. Легко видеть, что старший коэффициент произведения многочленов равен произведению старших коэффициентов множителей. Аналогично, свободный член произведения многочленов равен произведению свободных членов многочленов–множителей.
Пример 3. Упростим выражение (3х – 4)(2х + 1) – (х – 2)(6х + 3).
Умножим многочлен 3х – 4 на многочлен 2х + 1, а многочлен х – 2 – на многочлен 6х + 3 и вычтем из первого произведения второе:
(3х – 4)(2х + 1) – (х – 2)(6х + 3) = (6х 2 – 8х + 3х – 4) – (6х 2 + 3х – 12х – 6) =
= 6х 2 – 8х + 3х – 4 – 6х 2 – 3х + 12х + 6 = 4х + 2.
Это конспект по математике на тему «Произведение многочленов». Выберите дальнейшие действия:
Алгебра. 7 класс
Конспект урока
Перечень рассматриваемых вопросов:
Многочлен – сумма одночленов.
Любой многочлен можно разложить на два множителя, один из которых это число, не равное нулю.
Произведение нулевого многочлена на любой многочлен есть нулевой многочлен.
Чтобы найти произведение многочленов, необходимо каждый член одного многочлена умножить на каждый член другого многочлена, а полученные одночлены сложить.
Теоретический материал для самостоятельного изучения.
Это мы научились выполнять на предыдущем занятии.
Сегодня мы будем находить произведение многочленов.
Для начала выясним, что такое произведение многочленов.
Оказывается, произведение многочленов равно многочлену, членами которого являются произведения каждого члена другого многочлена. Т. е. чтобы найти произведение многочленов, необходимо каждый член одного многочлена умножить на каждый член другого многочлена, а полученные одночлены сложить.
Например, так выглядит произведение многочленов а + с и многочлена х + у.
Найдите произведение многочленов а + с и х + у.
Видно, что произведение двух многочленов не зависит от того, какой из многочленов будем мы умножать.
Если поменяем полученные равенства местами, то получим разложение многочлена на множители.
ах + ау + сх +су = (а + с)(х + у)
Введём определение разложения многочлена на множители.
Разложением многочлена на множители называют его преобразование в произведение двух или нескольких многочленов.
Пример. Разложите многочлен на множители
Для этого возьмём любое число, не равное нулю, например, пять, вынесем его за скобки. Получается разложение на множители, один из которых имеет нулевую степень (это число пять), а другой – ту же степень, что и исходный многочлен (степень многочлена один).
Стоит отметить, что, если при умножении многочленов, один из них не представлен (или записан) в нестандартном виде, то его сначала можно привести к стандартному виду, а затем выполнить вычисления. В противном случае вычисления могут быть более сложными.
Найдём двумя способами произведение многочленов (2а – 4с + а)( х + 3у +х).
Первый способ: сначала приведём к стандартному виду тот многочлен, который записан не в стандартном виде, и затем выполним умножение.
Второй способ: будем выполнять умножение сразу, а затем приводить полученный многочлен к стандартному виду.
Запись первым способом короче, но результат вычислений одинаковый.
Выполним ещё одно задание.
Найдём произведение многочленов.
Данное выражение будет равно нулю.
Следовательно, произведение нулевого многочлена на любой многочлен есть нулевой многочлен.
Доказательство: для доказательства данного равенства, воспользуемся формулой площади прямоугольника. S = ab, где а, b – стороны прямоугольника.
Для этого на рисунке выделим 6 прямоугольников (первый – со сторонами а и с, второй – со сторонами у и с, третий – со сторонами а и k, четвёртый – со сторонами а и х, пятый – со сторонами у и k, шестой – со сторонами у и х).
Чтобы найти площадь прямоугольника, состоящего из шести других, можно найти площадь каждого из шести прямоугольников, а затем сложить все найденные площади. Или сразу найти площадь прямоугольника, состоящего из шести других, как произведение двух его смежных сторон (а + у) и (с + k + х).
Что и требовалось доказать.
Разбор заданий тренировочного модуля.
1. Упростите выражение.
Это верное выражение.
Итак, сегодня мы получили представление о том, как находить произведение многочленов, раскрывать скобки, выполнять разложение многочленов на множители.
Разложение многочлена на множители
Разложить многочлен на множители означает представить его в виде произведения двух или нескольких многочленов.
Примером разложения многочлена на множители является вынесение общего множителя за скобки, поскольку исходный многочлен обращается в произведение двух сомножителей, один из которых является одночленом, а другой многочленом.
Разложение многочлена на множители способом вынесения общего множителя за скобки
При вынесении общего множителя за скобки образуется произведение из двух сомножителей, один из которых является одночленом, а другой многочленом. Например:
В рамках изучения многочленов, одночлен принято считать многочленом, состоящим из одного члена. Поэтому, когда в многочлене выносится за скобки общий множитель, то говорят что исходный многочлен представлен в виде произведения многочленов.
Разложение многочлена на множители способом группировки
Некоторые многочлены содержат группу членов, имеющих общий множитель. Такие группы можно заключать в скобки и далее выносить общий множитель за эти скобки. В результате получается разложение исходного многочлена на множители, которое называют разложением на множители способом группировки.
Рассмотрим следующий многочлен:
Далее в многочлене ax + ay + 3 x + 3 y члены 3x и 3y имеют общий множитель 3. Выпишем эти члены и тоже заключим их в скобки:
Теперь соединим выражения (ax + ay) и (3x + 3y) знаком «плюс»
Далее замечаем, что двучлен (x + y) является общим множителем. Вынесем его за скобки. Продолжаем решение в исходном примере. В результате получим:
Запишем решение покороче, не расписывая подробно, как каждый член был разделен на общий множитель. Тогда решение получится более компактным:
Пример 2. Разложить многочлен 9x + ax − 9y − ay на множители способом группировки.
В первой группе (9x − 9y) вынесем за скобки общий множитель 9. Во второй группе (ax − ay) вынесем за скобки за скобки общий множитель a
Далее вынесем за скобки двучлен (x − y)
Пример 3. Разложить многочлен ab − 3b + b 2 − 3a на множители способом группировки.
Во втором произведении b(−3 + b) в сомножителе (−3 + b) изменим порядок следования членов. Тогда получим b(b − 3)
Теперь вынесем за скобки общий множитель (b − 3)
Пример 4. Разложить многочлен x 2 y + x + xy 2 + y + 2xy + 2 на множители способом группировки.
Сгруппируем первый член многочлена со вторым, третий с четвёртым, пятый с шестым:
Далее замечаем, что многочлен (xy + 1) является общим множителем. Вынесем его за скобки:
Разложение многочлена на множители по формуле квадрата суммы двух выражений
Формулы сокращённого умножения, которые мы рассматривали в прошлом уроке, можно применять для разложения многочленов на множители.
Вспомним, как выглядит формула квадрата суммы двух выражений:
Поменяем местами левую и правую часть, получим:
Левая часть этого равенства является многочленом, а правая часть — произведением многочленов, поскольку выражение (a + b) 2 представляет собой перемножение двух сомножителей, каждый из которых равен многочлену (a + b).
Пример 1. Разложить на множители многочлен 4x 2 + 12xy + 9y 2
Полностью решение можно записать так:
Пример 2. Разложить на множители многочлен x 2 + 12x + 36
Разложение многочлена на множители по формуле квадрата разности двух выражений
Как и по формуле квадрата суммы двух выражений, многочлен можно разложить на множители по формуле квадрата разности двух выражений.
Формула квадрата разности двух выражений выглядит так:
Если в этой формуле поменять местами левую и правую часть, то получим:
Поскольку правая часть это произведение двух сомножителей, каждый из которых равен (a − b), то многочлен вида a 2 − 2ab + b 2 можно разложить на множители (a − b) и (a − b).
Пример 1. Разложить на множители многочлен 9x 2 − 12xy + 4y 2
Полностью решение можно записать так:
Пример 2. Разложить на множители многочлен x 2 − 4x + 4
Воспользуемся формулой квадрата разности двух выражений:
Разложение многочлена на множители по формуле куба суммы двух выражений
Вспомним, как выглядит формула куба суммы двух выражений:
Поменяем местами левую и правую часть, получим:
Левая часть этого равенства является многочленом, а правая часть — произведением многочленов, поскольку выражение (a + b) 3 представляет собой перемножение трёх сомножителей, каждый из которых равен многочлену (a + b).
Пример 1. Разложить на множители многочлен m 3 + 6m 2 n + 12mn 2 + 8n 3
Прежде чем применять формулу куба суммы, следует проанализировать данный многочлен. А именно, убедиться что перед нами действительно куб суммы двух выражений.
Первый член данного многочлена является результатом возведения в куб одночлена m
Последний член 8n 3 является результатом возведения в куб одночлена 2n
Второй член 6m 2 n является утроенным произведением квадрата первого выражения m и последнего 2n
Третий член 12mn 2 является утроенным произведением первого выражения m и квадрата последнего выражения 2n
Пример 2. Разложить на множители многочлен 125x 3 + 75x 2 + 15x + 1
Первый член данного многочлена является результатом возведения в куб одночлена 5x
Последний член 1 является результатом возведения в куб одночлена 1
Второй член 75x 2 является утроенным произведением квадрата первого выражения 5x и последнего 1
Третий член 15x является утроенным произведением первого выражения 5x и квадрата второго выражения 1
Разложение многочлена на множители по формуле куба разности двух выражений
Как и по формуле куба суммы двух выражений, многочлен можно разложить на множители по формуле куба разности двух выражений.
Вспомним, как выглядит формула куба разности двух выражений:
Если в этой формуле поменять местами левую и правую часть, то получим:
Поскольку правая часть это произведение трёх сомножителей, каждый из которых равен (a − b), то многочлен вида a 3 − 3a 2 b + 3ab 2 − b 3 можно разложить на множители (a − b), (a − b) и (a − b).
Пример 1. Разложить на множители многочлен 64 − 96x + 48x 2 − 8x 3
Прежде чем применять формулу куба разности, следует проанализировать данный многочлен. А именно, убедиться что перед нами действительно куб разности двух выражений.
Первый член данного многочлена является результатом возведения в куб одночлена 4
Последний член 8x 3 является результатом возведения в куб одночлена 2x
Второй член 96x является утроенным произведением квадрата первого выражения 4 и последнего 2x
Третий член 48x 2 является утроенным произведением первого выражения 4 и квадрата второго выражения 2x
3 × 4 × (2x) 2 = 3 × 4 × 4x 2 = 48x 2
Пример 2. Разложить на множители многочлен 27 − 135x + 225x 2 − 125x 3
Первый член данного многочлена является результатом возведения в куб одночлена 3
Последний член 125 является результатом возведения в куб одночлена 5x
Второй член 135x является утроенным произведением квадрата первого выражения 3 и последнего 5x
Третий член 225x 2 является утроенным произведением первого выражения 3 и квадрата второго выражения 5x
3 × 3 × (5x) 2 = 3 × 3 × 25x 2 = 225x 2
Разложение многочлена на множители по формуле разности квадратов двух выражений
Вспомним, как выглядит формула умножения разности двух выражений на их сумму:
Если в этой формуле поменять местами левую и правую часть, то получим:
Эту формулу называют разностью квадратов. Она позволяет разложить выражение вида a 2 − b 2 на множители (a − b) и (a + b).
Пример 1. Разложить на множители многочлен 16x 2 − 25y 2
Первый член 16x 2 является результатом возведения в квадрат одночлена 4x
Второй член 25y 2 является результатом возведения в квадрат одночлена 5y
Полностью решение можно записать так:
Пример 2. Разложить на множители многочлен x 2 − y 2
Чаще всего члены, из которых состоит исходная разность, являются результатами возведения во вторую степень каких-нибудь одночленов. Чтобы узнать чему в таком случае равны a и b, нужно как в первом примере представить члены исходной разности в виде одночленов возведённых в квадрат.
Полностью решение можно записать так:
Несмотря на простоту разложения по формуле разности квадратов, частые ошибки приходятся именно на эти задачи. Чтобы убедиться, что задача решена правильно, не мешает выполнить умножение в получившемся разложении. Если задача решена правильно, то должен получиться изначальный многочлен.
Проверим умножением данный пример. У нас должен получиться многочлен 4x 4 − 9y 6
Пример 4. Разложить на множители многочлен 81 − 64
Представим члены исходной разности в виде одночленов возведенных в квадрат. Далее воспользуемся формулой разности квадратов:
81 − 64 = 9 2 − 8 2 = (9 − 8)(9 + 8)
Разложение многочлена на множители по формуле сумме кубов двух выражений
Мы помним, что произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений:
Если в этой формуле поменять местами левую и правую часть, то получим формулу, называемую суммой кубов двух выражений:
Пример 1. Разложить на множители многочлен 27x 3 + 64y 3
Представим члены 27x 3 и 64y 3 в виде одночленов, возведённых в куб
Пример 2. Разложить на множители многочлен 125 + 8
Представим члены 125 и 8 в виде одночленов, возведённых в куб:
Далее воспользуемся формулой суммы кубов:
125 + 8 = 5 3 + 2 3 = (5 + 2)(25 − 10 + 4)
Разложение многочлена на множители по формуле разности кубов двух выражений
Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений:
Если в этой формуле поменять местами левую и правую часть, то получим формулу, называемую разностью кубов двух выражений:
Пример 1. Разложить на множители многочлен 64x 3 − 27y 3
Представим члены 64x 3 и 27y 3 в виде одночленов, возведённых в куб:
Пример 2. Разложить на множители многочлен 64 − 27
Представим члены 64 и 27 в виде одночленов, возведённых в куб:
64 − 27 = 4 3 − 3 3 = (4 − 3)(16 + 12 + 9)
Пример 3. Разложить на множители многочлен 125x 3 − 1
Представим члены 125x 3 и 1 в виде одночленов, возведённых в куб:
Разложение многочлена на множители различными способами
К некоторым многочленам можно применять различные способы разложения на множители. Например, к одному многочлену можно применить способ вынесения общего за скобки, а затем воспользоваться одной из формул сокращённого умножения.
Пример 1. Разложить на множители многочлен ax 2 − ay 2
При этом в скобках образовался многочлен, который является разностью квадратов. Применив формулу разности квадратов. Тогда получим:
Пример 2. Разложить на множители многочлен 3x 2 + 6xy + 3y 2
Вынесем за скобки общий множитель 3