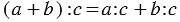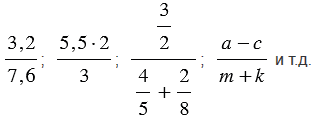Что значит представить в виде дроби выражение
Преобразование рациональных выражений: виды преобразований, примеры
Статья рассказывает о преобразовании рациональных выражений. Рассмотрим виды рациональных выражений, их преобразования, группировки, вынесения за скобки общего множителя. Научимся представлять дробные рациональные выражения в виде рациональных дробей.
Определение и примеры рациональных выражений
Выражения, которые составлены из чисел, переменных, скобок, степеней с действиями сложения, вычитания, умножения, деления с наличием черты дроби, называют рациональными выражениями.
То есть это такие выражения, которые не имеют деления на выражения с переменными. Изучение рациональных выражений начинается с 8 класса, где их называют дробными рациональными выражениями. Особое внимание уделяют дробям в числителе, которые преобразовывают с помощью правил преобразования.
Это позволяет переходить к преобразованию рациональных дробей произвольного вида. Такое выражение может быть рассмотрено как выражение с наличием рациональных дробей и целых выражений со знаками действий.
Основные виды преобразований рациональных выражений
Рациональные выражения используются для того, чтобы выполнять тождественные преобразования, группировки, приведение подобных, выполнение других действий с числами. Цель таких выражений – это упрощение.
Преобразуем в числителе формулу разности квадратов, тогда получаем, что
Представление в виде рациональной дроби
Алгебраическая дробь чаще всего подвергается упрощению при решении. Каждое рациональное приводится к этому разными способами. Необходимо выполнить все необходимые действия с многочленами для того, чтобы рациональное выражение в итоге смогло дать рациональную дробь.
Следует начать с умножения, тогда получим, что
Производим представление полученного результата с исходное. Получим, что
Теперь выполняем вычитание:
После деления придем к рациональной дроби вида
Можно решить это иначе.
Деление и дроби
Не всегда можно одно натуральное число разделить на другое, так, например, 2 нельзя разделить на 3, в таком случае деление можно заменить дробью 

Пример:
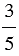
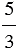
| В результате деления двух натуральных чисел может получится натуральное число или дробное число. |
Пример:
20 : 4 = 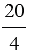
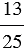
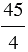
| Всякое натуральное число может быть записано в виде дроби, причем натуральное число можно представить в виде дроби с каким угодно знаменателем. |
Пример:
Получаем, что число 1 можно представить в виде дроби, у которой числитель и знаменатель равны.
Свойство деления суммы на число
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные.
Пример:
(64 + 72) : 8 = 64 : 8 + 72 : 8 = 8 + 9 = 17.
Дробные выражения
| Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением. |
К дробным выражениям относятся:
Обратите внимание, в числителе и в знаменателе дробного выражения могут стоять любые числа (натуральные числа, обыкновенные дроби, десятичные дроби и т.д.), а также числовые или буквенные выражения (смотри примеры выше).
Если числитель и знаменатель дробного выражения разделить или умножить на одно и то же число отличное от нуля, то получим дробное выражение, равное данному. Данное свойство часто используют, когда преобразуют дробное выражение с десятичными дробями в обыкновенную дробь.
Пример:
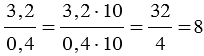
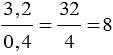
То есть, получается, что мы переносим запятую в числителе и знаменателе дробного выражения на одинаковое количество цифр вправо, при этом если в одном числе цифр после запятой больше, чем в другом, то переносим запятую на большее количество цифр, а там где цифр после запятой меньше дописываем нули.
Пример:
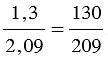
Поделись с друзьями в социальных сетях:
Алгебра
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
Понятие рационального выражения
В 5 и 6 классе мы уже изучали дроби и действия над ними. В 7 классе рассматривались рациональные числа, которые, по сути, и являются дробями. Однако до этого мы изучали только так называемые числовые дроби, у которых в числителе и знаменателе стоят какие-то числа либо выражения с числами, но не переменные величины.
Следующие дроби являются числовыми:
Однако нередко в алгебре приходится иметь дело и с дробями, которые содержат переменные. В качестве примера подобных выражений можно привести:
Так как деление на ноль является недопустимой операцией в алгебре, то некоторые дроби могут не иметь смысла. Так, дробь
бессмысленна, так как ее знаменатель 21 – 3•7 равен нулю.
Если дробь содержит переменные величины, то ее значение зависит от этих переменных. Так, дробь
при у = 4 принимает значение, равное 9. Если же у = 3, то эта дробь окажется бессмысленной.
Значения переменных величин, при которых дробь сохраняет свой смысл, называют допустимыми значениями переменных.
Пример. Укажите множество допустимых значений величин х и у для дроби
Решение. Недопустим только случай, при котором в знаменателе находится ноль, то есть когда выполняется равенство
или равносильное ему равенство
Следовательно, допустимыми значениями являются все такие пары (х; у), что х ≠ у.
Пример. Каковы допустимые значения величин а и b в дроби
Решение. В данной записи есть три дробных черты, а значит, и три знаменателя:
Ни один из знаменателей не должен равняться нулю, поэтому
Перенесем в последнем неравенстве 2-ое слагаемое вправо, изменив знак (правила преобразований выражений со знаком ≠ точно такие же, как и у равенств):
По свойству пропорции имеем:
Итак, допустимыми являются все значения a и b, при которых а ≠ 0, b≠ 0, a≠b.
Пример. Найдите множество допустимых значений х для дроби
Ясно, что знаменатель должен отличаться от нуля:
Чтобы найти, при каких значениях неизвестной величины знаменатель обращается в ноль, надо решить уравнение
Представим полином в левой части как произведение, применив формулу квадрата разности:
Получаем, что исходная дробь сохраняет смысл при любых х, отличных от – 5 и 5.
Порою дроби, содержащие переменные, могут встречаться в тождествах.
Пример. Докажите тождество
Решение. У дроби в левой части знаменатель всегда положителен, поэтому все допустимыми являются все значения c. Согласно свойству операции деления, делимое равно произведению делителя и частного, поэтому для доказательства тождества надо лишь показать справедливость равенства
(с 3 – 2с 2 + с – 2) = (с – 2)(с 2 + 1)
Раскроем скобки в правой части:
(с – 2)(с 2 + 1) = с 3 – 2с 2 + с – 2
Получили одинаковое выражение и для левой, и для правой части тождества, следовательно, оно верное.
Теперь сформулируем понятие рационального выражения.
Среди рациональных выражений выделяют целые и дробные выражения.
Приведем примеры целых рациональных выражений:
А вот несколько примеров дробных рациональных выражений:
Стоит заметить, что дробь и дробное выражение – это два разных понятия. Для иллюстрации приведем два примера:
Отдельно отметим, что дробь равна нулю тогда, когда ее числитель равен нулю, а знаменатель нет. Если же и знаменатель равен нулю, то получается недопустимое действие – деление на ноль, поэтому дробь не будет иметь смысла.
Пример. Найдите все корни уравнения
Решение. На первый взгляд уравнение кажется сложным, особенно из-за знаменателя. Однако он здесь почти не играет роли. В левой части находится дробь, значит, нулю равен ее знаменатель:
х – 1 = 0 или х + 2 = 0
Получили два корня. Осталось убедиться, что при этих значениях х дробь не становится бессмысленной, то есть ее знаменатель не обращается в ноль. При х = 1 имеем знаменатель
2•1 4 – 3•1 3 + 5•1 – 4 = 2 – 3 + 5 – 4 = 0
поэтому число 1 НЕ является корнем уравнения. Теперь проверим знаменатель при х = – 2:
2•(– 2) 4 – 3•( – 2) 3 + 5•( – 2) – 4 =
Получается, что единственное корень уравнения – это ( – 2).
Сокращение рациональных выражений
Узнав, какие выражения являются рациональными, мы приступим к изучению их преобразований. Напомним главное свойство дроби:
Оно означает, что числитель и знаменатель можно умножить на произвольное число (кроме нуля), то значение дроби останется прежним:
Это правило остается верным и в том случае, когда вместо чисел используются переменные величины.
Например, возможны такие преобразования рациональных выражений:
Например, пусть надо привести дробь
6а 2 b 2 = 2а 2 b•3b
Поэтому выражения над и под дробной чертой надо умножить на 3b:
Использованный нами множитель 3b называют дополнительным множителем.
Обратная операция, при которой из знаменателя и числителя убирают совпадающие множители, называется сокращением дроби:
Это тождество означает, что дроби можно сокращать, убирая общий множитель, например:
Аналогичные действия можно совершать не только с числовыми дробями, но и с дробными выражениями:
В последнем примере мы вынесли общие множители за скобки (2х и 7у), чтобы над и под чертой появилась одинаковая сумма х + 3у, которую можно сократить.
Однако при сокращении дробей важно учитывать область ее допустимых значений, ведь из-за изменения знаменателя она может измениться. Например, пусть требуется построить график функции
В числителе стоит разность квадратов, которую можно разложить на множители:
Казалось бы, мы получили линейную функцию
чей график нам известен – это прямая. Но она определена при всех возможных х, в то время как исходная дробь бессмысленна при х = 2, ведь тогда знаменатель становится равен нулю. Поэтому график функции будет выглядеть как прямая, однако одна из ее точек, с координатами (2; 4), будет «выколотой» точкой, и исключенной:
Данный рисунок означает, что графиком функции – прямая линия, кроме точки (2; 4)
Выколотая точка на графике изображается маленьким незакрашенным кружочком.
Следующее важное свойство дроби связано со знаком минус. Знак, стоящий перед дробью, можно перенести либо в знаменатель, либо в числитель:
Также напомним, что можно поменять местами уменьшаемое и вычитаемое в скобках, если изменить перед ней знак:
Применение этих правил позволяет упрощать некоторые дроби, например:
Более сложный пример:
Рассмотрим такое понятие, как однородный многочлен. Так называют тот полином, у которого все одночлены имеют одинаковую степень.
Подробнее о степени одночлена можно узнать в этом уроке. Если коротко, то степень одночлена – эта сумма степеней у всех переменных, входящих в его буквенную часть. Например, у следующих мономов степень равна 4:
В отношении однородных полиномов, состоящих из двух переменных, можно применять особый прием. Достаточно поделить его на одну из переменных в степени полинома, и получится выражение, зависящее только от одной дроби. Поясним это на примере. Пусть надо вычислить значение отношения
если известно другое отношение:
В исходной дроби представляет собой отношение двух однородных полиномов третьей степени. Поэтому поделим их на y 3 (можно было делить и на х 3 ). При этом значение дроби не изменится, ведь мы делим числитель и знаменатель на одинаковый моном:
Получили выражение, которое зависит только от отношения
Попытаемся найти эту величину из условия
Отсюда следует, что
Теперь подставим найденное отношение в формулу(1):
До этого мы рассматривали примеры дробных выражений, состоящие из полиномов с целыми коэффициентами. Если же используются дробные числа, то от них всегда можно избавиться, домножив дробь на какое-нибудь число.
Например, дана дробь
Коэффициенты при у и у 2 дробные. Избавимся от них. Для этого используем дополнительный множитель 12:
Далее рассмотрим сложение и вычитание дробных выражений. Проще всего эту операцию проводить в том случае, когда у дробей совпадают знаменатели. В такой ситуации используются уже нам известные правила:
Сложим две величины:
В их знаменателе стоит одинаковый полином, а потому операция будет выглядеть так:
Здесь мы в числителе использовали формулу квадрата разности.
Теперь вычтем из выражения
У них совпадают знаменатели, поэтому проблем с вычитанием не возникает:
Заметим, что обычно у дробных выражения стараются сокращать до тех пор, пока не получится несократимая дробь.
Если у дробей различные знаменатели, то приводят к общему знаменателю, домножая их на какой-нибудь дополнительный множитель.
Рассмотрим следующий пример:
Есть и более простой способ найти общий знаменатель, для этого достаточно просто перемножить знаменатели дробей-слагаемых. Однако дальнейшие преобразования будут более долгими. Решим таким путем тот же пример:
В числителе возможно вынесение общего множителя 2ху за скобки:
Видно, что конечный результат операции не изменился.
Если в знаменателях складываемых дробей стоят многочлены, то стоит попробовать разложить их на множители. За счет этого порою удается найти более простой общий знаменатель.
Пусть надо сложить выражения
Вынесем в знаменателях за скобки множители х и у:
В знаменателях есть похожие множители, (3х – у) и (у – 3х). Чтобы они оказались одинаковыми, надо поменять местами вычитаемое и уменьшаемое в одних скобках. Для этого перед ними надо добавить знак «минус»:
Общим множителем этих дробей является произведение ху(3х – у):
Осталось разложить числитель, где стоит разность квадратов:
Следующий важный навык, который может потребоваться при работе с рациональными выражениями – это выделение целой части из дроби.
Продемонстрируем эту операцию на примере
Перепишем дробь, поменяв порядок слагаемых в числителе:
И в знаменателе, и в числителе есть сумма х 2 + 1. Теперь можно произвести выделение целой части:
В справедливости данного преобразования можно убедиться, выполнив его «в обратную сторону»:
Любой многочлен можно сделать дробью, если приписать ему числитель, равный 1. Пусть надо упростить формулу
Заменим 2х – 1 на дробь и произведем вычитание:
Упростить далее эту дробь довольно сложно, но всё же возможно. Для этого надо заменить одночлен (– 3х 2 ) на разность (– х 2 – 2х 2 ), а 14х на сумму (6х+8х). Посмотрим, что получится в результате:
Складывать можно и более двух дробей. Пусть надо упростить сумму
Будем складывать слагаемые последовательно, то есть сначала сложим два первых слагаемых, потом к результату добавим третье, а далее и 4-ое слагаемое:
Представление дроби в виде суммы дробей
Сумму двух дробей можно представить в виде несократимой дроби единственным образом, например:
Однако у обратной задачи, разложения одной дроби на сумму нескольких других, есть бесконечной множество решений:
То же самое верно в отношении дробных выражений. Например,
можно разложить так:
С другой стороны, это же выражение можно представить в следующем виде:
Для раскладывания дроби на сумму дробей можно воспользоваться методом неопределенных коэффициентов, предложенным Рене Декартом в 1637 году. Покажем, как его использовать, на примере. Пусть надо представить в виде суммы двух дробей отношение
Заметим, что знаменатель х 2 – 4 можно записать как произведение полиномов первой степени (х – 2)(х + 2):
Это означает, что исходное выражение можно представить как сумму дробей со знаменателями (х – 2) и (х + 2). Обозначим числители в этих дробях как неизвестные величины aи b (они и носят название неопределенных коэффициентов). Тогда можно записать, что
Задача сводится к тому, чтобы найти a и b. Для этого преобразуем сумму дробей:
Полученная дробь должна равняться исходной дроби:
У правой и левой части равны знаменатели, а значит, должны равняться и числители:
(a + b)x + (2a– 2b) = 2x + 6
Это тождество может быть верным только тогда, когда справа и слева равны коэффициенты перед переменной х, а также свободные члены, поэтому можно записать систему:
Решив эту систему, мы сможем найти значения a и b. Используем метод подстановки, выразив а из первого уравнения:
Подставим эту формулу во второе уравнение:
а = 2 – b = 2 – (– 2,5) = 2 + 2,5 = 4,5
Итак, получили, что a = 4,5 и b = – 2,5. Это значит, исходную дробь можно разложить следующим образом:
Теперь рассмотрим, как производится умножение и деление дробных выражений. Эти действия аналогичны операциям с обычными числами, которые уже изучались в 5 классе. Напомним две основные формулы:
Пусть требуется перемножить величины
Эта операция осуществляется так:
Теперь посмотрим, как выполняется деление:
Деление заменяется умножением на дробь, обратную делителю:
Для упрощения выражений часто используют формулы сокращенного умножения:
При возведении дроби в степень надо отдельно возводить в степени знаменатель и числитель:
Вообще для любого натурального числа nбудет верным тождество:
Пусть надо возвести в 4-ую степень дробь
Выглядеть это будет так:
Преобразование рациональных выражений
Если у дроби в знаменателе и числителе записаны полиномы, то ее называют рациональной дробью. В виде рациональной дроби можно записать любое рациональное выражение.
Пусть надо записать в виде рациональной дроби выражение
Сначала выполним вычитание в скобках, а потом и деление:
Обратим внимание, что выражение
представляет собой не что иное, как разность квадратов, для которой можно применить формулу сокращенного умножения:
(2а + 1) 2 – (2а – 1) 2 = (2а + 1 + 2а – 1)( 2а + 1 – (2а – 1)) =
= (2а + 1 + 2а – 1)( 2а + 1 – 2а + 1).
Используя это, продолжим работать с дробью:
Однако иногда удобнее не производить вычисления в скобках, а использовать распределительный закон умножения:
Пусть требуется упростить произведение:
Сначала раскроем скобки:
Часто проблемы возникают с так называемыми «многоэтажными» дробями. Так называют дроби, у которых в числителе и знаменателе стоят другие дробные выражения. Выглядят они внушительно, однако правила работы с ними такие же, как и с другими выражениями. Каждая дробная черта просто означает операцию деления.
Пусть требуется выполнить преобразование дробного рационального выражения
Сначала представим эту дробь как операцию деления:
Теперь в каждой из скобок произведем сложение: