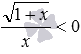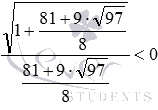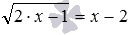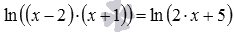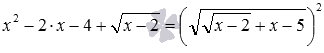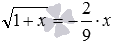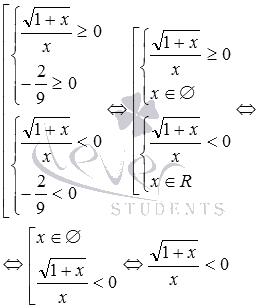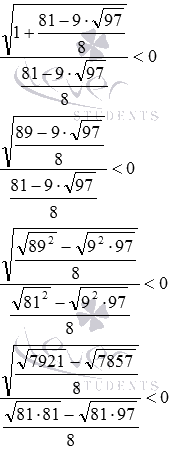Что значит посторонний корень
Посторонний корень
Смотреть что такое «Посторонний корень» в других словарях:
Уравнение — в математике, аналитическая запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны. Аргументы, от которых зависят эти функции, называются обычно неизвестными, а значения неизвестных, при которых… … Большая советская энциклопедия
Уравнение — Первое печатное появление знака равенства в книге Роберта Рекорда в 1557 году (записано уравнение ) Уравнение это равенство вида или, в приведённой форме … Википедия
ГИБУ Николай Трофимович — (р. 19 ноября 1936, село Озерное, Одесская область), режиссер, сценарист. Окончил сценарный факультет ВГИКа (1966, мастерская К.Парамоновой и В.Ежова). С 1966 сценарист и редактор Комитета по кинематографии Молдавской ССР, с 1970 режиссер к/ст… … Энциклопедия кино
Успенский Глеб Иванович — Успенский (Глеб Иванович) известный писатель. Родился 14 ноября 1840 г. в Туле, где его отец, сын сельского дьячка, служил секретарем палаты государственных имуществ. Учился в тульской и черниговской гимназиях; поступил сначала в Петербургский… … Биографический словарь
Успенский, Глеб Иванович — известный писатель. Род. 14 ноября 1840 г. в Туле, где его отец, сын сельского дьячка, служил секретарем палаты государственных имуществ, умер в 1902 г. Учился в тульской и черниговской гимназиях; поступил сначала в Петербургский университет по… … Большая биографическая энциклопедия
Сахар свекловичный и тростниковый* — I. Химия. II. Техническое производство. III. Статистика. IV. Акциз на сахар. V. Сахарная нормировка. VI Сахар в международной торговле. I. С. (хим. С 12 Н 22 О 11). Нахождение и добывание свекловичного и тростникового С. см. ниже. С.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Успенский Глеб Иванович — I известный писатель. Род. 14 ноября 1840 г. в Туле, где его отец, сын сельского дьячка, служил секретарем палаты государственных имуществ. Учился в тульской и черниговской гимназиях; поступил сначала в Петербургский унив. по юридическому… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Сахар свекловичный и тростниковый — I I. Химия. II. Техническое производство. III. Статистика. IV. Акциз на сахар. V. Сахарная нормировка. VI Сахар в международной торговле. I. С. (хим. С12Н22О11). Нахождение и добывание свекловичного и тростникового С. см. ниже. С. кристаллизуется … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ЛУЧКО Клара Степановна — (1 июля 1925, село Чутово, Полтавская область 26 марта 2005, Москва), российская актриса, народная артистка СССР (1985). Лауреат Сталинской премии (1951, за роль Даши Шелест в фильме «Кубанские казаки»). Дебют актрисы в кино состоялся в 1940 году … Энциклопедия кино
ТОМА Светлана Андреевна — (наст. Фомичева) (р. 24 марта 1947, Кишинев), российская киноактриса, заслуженная артистка Молдавии (1979). Первая роль в кино Иоанна в фильме Эмиля Лотяну «Красные поляны» (1966). Училась на юридическом факультете Кишиневского университета,… … Энциклопедия кино
Посторонние корни уравнения, отсеивание посторонних корней
Решение уравнений через переход к уравнениям-следствиям может привести к появлению так называемых посторонних корней. В этой статье мы, во-первых, детально разберем, что такое посторонние корни. Во-вторых, поговорим о причинах их возникновения. И в-третьих, на примерах рассмотрим основные способы отсеивания посторонних корней, то есть, проверки корней на предмет наличия среди них посторонних с целью исключения их из ответа.
Посторонние корни уравнения, определение, примеры
В школьных учебниках по алгебре не дается определение постороннего корня. Там представление о постороннем корне формируется путем описания следующей ситуации: при помощи некоторых преобразований уравнения осуществляется переход от исходного уравнения к уравнению-следствию, находятся корни полученного уравнения-следствия, и осуществляется проверка найденных корней подстановкой в исходное уравнение, которая показывает, что некоторые из найденных корней не являются корнями исходного уравнения, эти корни называют посторонними корнями для исходного уравнения [1, с. 174-175; 2, с. 202; 3, с. 187-188].
Отталкиваясь от этой базы, для себя можно принять такое определение постороннего корня:
Посторонние корни – это корни полученного в результате проведения преобразований уравнения-следствия, не являющиеся корнями исходного уравнения.
Причины возможного появления посторонних корней
Если для получения уравнения-следствия не использовать никакие «экзотические» преобразования, а использовать только основные преобразования уравнений, то посторонние корни могут возникнуть лишь по двум причинам:
Здесь стоит напомнить, что расширение ОДЗ в результате преобразования уравнения в основном происходит
Что такое отсеивание посторонних корней?
Термин «отсеивание посторонних корней» лишь с натяжкой можно назвать устоявшимся, он встречается далеко не во всех учебниках алгебры, но является интуитивно понятным, из-за чего обычно и используется. Что понимают под отсеиванием посторонних корней, становится понятно из следующей фразы: «… проверка – обязательный этап решения уравнения, который поможет обнаружить посторонние корни, если они есть, и отбросить их (обычно говорят «отсеять»)» [1, с.176].
Отсеивание посторонних корней – это обнаружение и отбрасывание посторонних корней.
Теперь можно переходить к способам отсеивания посторонних корней.
Способы отсеивания посторонних корней
Проверка подстановкой
Основной способ отсеивания посторонних корней – это проверка подстановкой. Он позволяет отсеять посторонние корни, которые могли возникнуть и по причине расширения ОДЗ, и по причине возведения обеих частей уравнения в одну и ту же четную степень.
Проверка подстановкой состоит в следующем: найденные корни уравнения-следствия по очереди подставляются в исходное уравнение или в любое равносильное ему уравнение, те из них, которые дают верное числовое равенство, являются корнями исходного уравнения, а те, которые дают неверное числовое равенство или выражение, не имеющее смысла, являются посторонними корнями для исходного уравнения.
Покажем на примере, как проводится отсеивание посторонних корней через подстановку в исходное уравнение.
Решите уравнение
В некоторых случаях отсеивание посторонних корней целесообразнее проводить другими способами. Это относится в основном к тем случаям, когда проверка подстановкой связана со значительными вычислительными трудностями или когда стандартный способ решения уравнений какого-то определенного вида предполагает другой проверки (например, отсеивание посторонних корней при решении дробно-рациональных уравнений проводится по условию не равенства нулю знаменателя дроби). Разберем альтернативные способы отсеивания посторонних корней.
По ОДЗ
В отличие от проверки подстановкой, отсеивание посторонних корней по ОДЗ уместно не всегда. Дело в том, что этот способ позволяет отсеивать лишь посторонние корни, возникающие по причине расширения ОДЗ, и он не гарантирует отсеивание посторонних корней, которые могли возникнуть по другим причинам, например, из-за возведения обеих частей уравнения в одну и ту же четную степень. Более того, не всегда просто отыскать ОДЗ для решаемого уравнения. Тем не менее, способ отсеивания посторонних корней по ОДЗ стоит держать на вооружении, так как часто его использование требует меньших вычислительных работ, чем использование других способов.
Отсеивание посторонних корней по ОДЗ проводится следующим образом: все найденные корни уравнения-следствия проверяются на предмет принадлежности области допустимых значений переменной для исходного уравнения или любого равносильного ему уравнения, те из них, которые принадлежат ОДЗ, являются корнями исходного уравнения, а те из них, которые не принадлежат ОДЗ, являются посторонними корнями для исходного уравнения.
Анализ приведенной информации приводит к выводу, что отсеивание посторонних корней по ОДЗ целесообразно проводить, если единовременно:
Покажем, как проводится отсеивание посторонних корней, на практике.
Решите логарифмическое уравнение
По условиям ОДЗ
Как мы сказали в предыдущем пункте, если посторонние корни могли возникнуть лишь по причине расширения ОДЗ, то их можно отсеять по ОДЗ для исходного уравнения. Но не всегда просто найти ОДЗ в виде числового множества. В таких случаях можно проводить отсеивание посторонних корней не по ОДЗ, а по условиям, определяющим ОДЗ. Разъясним, как проводится отсеивание посторонних корней по условиям ОДЗ.
Найденные корни по очереди подставляются в условия, определяющие ОДЗ для исходного уравнения или любого равносильного ему уравнения. Те из них, которые удовлетворяют всем условиям, являются корнями уравнения. А те из них, которые не удовлетворяют хотя бы одному условию или дают не имеющее смысла выражение, являются посторонними корнями для исходного уравнения.
Приведем пример отсеивания посторонних корней по условиям ОДЗ.
Решить иррациональное уравнение
Отсеивание посторонних корней, возникающих из-за возведения обеих частей уравнения в четную степень
Понятно, что отсеивание посторонних корней, возникающих из-за возведения обеих частей уравнения в одну и ту же четную степень, можно осуществить путем подстановки в исходное уравнение или в любое равносильное ему уравнение. Но такая проверка может быть связана со значительными вычислительными трудностями. На этот случай стоит знать альтернативный способ отсеивания посторонних корней, о котором мы сейчас и поговорим.
Покажем, как на практике отсеиваются посторонние корни указанным способом.
Решите уравнение
В заключение скажем, что рассмотренный подход является частным случаем более общего подхода к отсеиванию посторонних корней, возникающих при возведении обеих частей уравнения в одну и ту же четную степень. Отсеять посторонние корни, которые могут возникнуть при возведении обеих частей уравнения f(x)=g(x) в одну и ту же четную степень, можно по условию 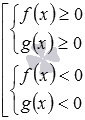
Приведем пример отсеивания посторонних корней предложенным способом. Возьмем уравнение 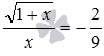
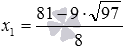

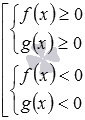
Подстановка в неравенство 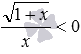
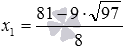
Полученное неравенство верное, так как в числителе положительное число, а в знаменателе – отрицательное, поэтому, отношение этих чисел есть отрицательное число. Значит, 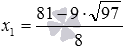
Подстановка в неравенство