Что значит после числа

Значимые цифры: правила, примеры, решенные упражнения

Содержание:

А что происходит, когда число целое? Это означает, что он известен с максимально возможной точностью, другими словами, он имеет бесконечную точность. Например, при подсчете людей, животных или таких предметов, как книги и телефоны, результатом будет точное целое число.

Если мы скажем, что в кинотеатре 110 человек смотрят фильм, это точное число, ни много, ни мало, и оно состоит из трех значащих цифр.

Значительные числа обрабатываются по некоторым простым правилам, которые запоминаются после небольшой практики, как мы увидим дальше.

Правила определения значащих цифр числа

Правило 1

Начальные нули не считаются значащими цифрами, поэтому 0,045 и 4,5 имеют две значащие цифры, поскольку они начинают отсчет слева и начиная с первой ненулевой цифры.

Правило 2

Нули после (справа) первой значащей цифры действительно считаются значащей цифрой (если это оправдано точностью измерительного прибора).

Наконец, нули в середине также считаются значащей цифрой.

Правило 3

Для чисел, записанных в экспоненциальном представлении, все цифры в мантиссе значимы, а показатель степени не влияет на точность.

Правило 4

При выполнении операций с десятичными знаками, например при вычислении площадей или других подобных операций, результат должен иметь такое же количество значащих цифр, что и количество с наименьшим количеством значащих цифр, участвовавших в операции. Это правило действует для любых арифметических операций.

Правило 5

Знак числа не влияет на количество его значащих цифр.

Мы сразу же увидим некоторые примеры этого и всех других правил.

Примеры

Пример 1

Найдите, сколько значащих цифр в каждом из этих чисел.

Ответы

а) 876 имеет 3 значащих цифры.

б) 1000,68 имеет 6 значащих цифр, поскольку нули в середине считаются как таковые.

c) Вместо 0,00005026 имеется 4 значащих цифры. Обратите внимание, что 5 нулей слева от 5 не считаются значащими цифрами, тогда как 0 между 5 и 2 считается.

г) 4.8 имеет 2 значащих цифры.

Пример 2

Обычно измерения проводят с помощью измерительных инструментов, таких как рулетки, часы, термометры, весы и т. Д. Со сколькими значащими цифрами мы должны указывать количества, которые мы измеряем таким образом?

Ответить

Это зависит от оценки инструмента, которым он измеряется. Возьмем пример: измерьте внешний диаметр трубы с помощью градуированной линейки и штангенциркуля.

Он более точен, чем градуированная линейка, потому что с его помощью мы можем узнать более значащие числа определенной длины.

Вот почему нет смысла сообщать периметр, скажем, 35,88 см, если мы измеряем его рулеткой, поскольку этот инструмент недостаточно точен, чтобы указать такое количество значащих цифр.

Оценка рулетки A определяется по:

Пример 3

Сколько значащих цифр в показании цифрового термометра?

Ответить

Термометр на рисунке показывает трехзначные показания температуры. Однако в показанном измерении 36,6 ºC только первые две цифры слева направо являются точными, поскольку на десятичную дробь влияет погрешность оценки прибора, которая обычно указывается на задней стороне прибора или на ваше руководство по эксплуатации.

Обычно для представленного типа цифрового прибора погрешность оценки составляет 0,1 ºC. Этого достаточно, чтобы быть уверенным, что у вас нет температуры.

Правила округления чисел

При использовании калькулятора для выполнения расчетов с полученными измерениями некорректно давать результат, используя все цифры, которые появляются на экране.

Сохраняются только те, которые точно известны, поскольку только они имеют истинное значение. Затем необходимо округлить результаты, чтобы они соответствовали количеству точно известных цифр. Вот эти правила:

-Если число, следующее за цифрой, которую необходимо скрыть, является равно или больше 5, к этой цифре добавляется 1.

Например, при округлении 3,786 до двух десятичных знаков мы хотим сохранить числа до 8. Поскольку число, следующее за (6), больше 5, 8 становится 8 + 1 = 9, и число остается как 3.79.

-Когда число, следующее за цифрой, которую необходимо сохранить, менее 5, цифра останется прежней.

Если мы хотим округлить 1,27924, чтобы у него было только 3 десятичных разряда, это достигается путем достижения 9, за которым следует 2. Поскольку 2 меньше 5, эти десятичные дроби исчезают, а округленное число остается 1,279.

Упражнение решено

Обеденный стол имеет форму и размеры, указанные на прилагаемом рисунке. Вам предлагается рассчитать его площадь по правилам работы со значащими цифрами.

Решение

Зона стола может быть разделена на центральную прямоугольную зону и два полукруга, по одному с каждой стороны, которые вместе составляют один полный круг.

Мы будем называть A₁ к площади прямоугольника, задаваемой:

К₁ = основание × высота = 2,5 м x 1,0 м = 2,5 м 2

Со своей стороны, площадь круга, равная площади 1 полукруга, умноженной на 2, равна:

Диаметр любого из полукругов составляет 1,0 м, поэтому радиус равен 0,50 м. Диаметр также можно использовать напрямую для расчета площади, в этом случае:

К₂ = (π × диаметр 2 ) / 4

К₂ = [π x (1,0 м) 2 ] / 4 = 0,785398163 м 2

Были использованы все цифры, предоставленные калькулятором. Теперь добавляем A₁ уже₂ для общей площади стола A:

A = (2,5 + 0,785398163) м 2 = 3,285398163 м 2

Поскольку размеры таблицы известны до двух значащих цифр, не имеет смысла выражать результат со всеми десятичными знаками, указанными калькулятором, который никогда не дает количество значащих цифр в результате.

Что вам нужно сделать, так это округлить область так, чтобы в ней было такое же количество значащих цифр, что и размеры таблицы, то есть 2. Таким образом, окончательный результат будет представлен следующим образом:

Ссылки

3 типа ускорителей частиц (и их характеристики)

10 лучших гериатрических резиденций в Сантандере

Источник

Как легко понять знаки Σ и П с помощью программирования

Для тех, кто подзабыл матешу

Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.

Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.

Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.

Знак Σ — сумма

Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:

Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.

На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:

Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».

Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:

Произведение П

С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:

А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:

Что дальше

Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.

Источник

Разряды и классы чисел

Числа и цифры

Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.

Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.

Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …

От количества цифр в числе зависит его название.

Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.

Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.

Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.

Каждая цифра в записи многозначного числа занимает определенное место — позицию.

Классы чисел

Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.

Названия классов многозначных чисел справа налево:

Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:

А теперь прочитаем число единиц каждого класса слева направо:

Разряды чисел

От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:

Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.

Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.

У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.

Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.

Низший (младший) разряд многозначного натурального числа — разряд единиц.

Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.

Разрядные единицы обозначают так:

Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.

Чтобы легче понимать математику — записывайтесь на наши курсы по математике!

Потренируемся

Пример 1. Записать цифрами число, в котором содержится:

Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:

Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.

Пример 2. Сколько сотен содержится в числе 6284?

В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.

Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.

Значит, в данном числе содержится 62 сотни.

Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.

Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:

Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.

Источник

Что означают последние 2 цифры в паспорте внизу после галочки?

Для многих номер паспорта скрывает в себе какую-то магию: по какой логике высчитываются эти цифры. Почему тому или иному человеку достаются именно те числа, которые он получил, что означают последние две цифры в паспорте внизу после галочки и влияют ли они на что-либо? В действительности, номер паспорта вычисляется не случайно, а для этого существует специальная формула, которая утверждена на законодательном уровне. И каждая цифра в паспорте взята не с потолка, а высчитана по этой закономерности. Кроме того, она несёт в себе какой-то смысл и значение. И ничего скрытого и секретного в этом нет.

В этой статье разбираем значение последних 2 цифр в нижней строке номера паспорта после символа меньше «

Значение последней цифры нижней строки номера паспорта

Последняя цифра является одним из контрольных чисел. Контрольное число, как понятно по названию, необходимо для контроля за правильностью всех введённых данных.

Контрольные числа используются во многих областях, кроме паспорта они бывают и на других документах, а также применяются не только в обороте документов. Они помогают защитить большое количество данных от случайных ошибок. В паспорте ошибки недопустимы. Особо широкое распространение контрольные числа получили в компьютерной области, где они используются для проверки правильности файлов и называются биты чётности, код Рида-Соломона и CRC.

И, конечно же, последние цифры в нижней строке номера паспорта не являются количеством людей с таким же именем. Об этом говорят многие, но это не правда.

Как контрольные числа помогают минимизировать риск ошибок?

Рассмотрим на простом примере. Представьте себе несложный массив данных, состоящий, допустим, из даты рождения гражданина — 9 августа 1980 года, даты выдачи документа — 25 мая 2015 года, кода органа, который выдал документ — 475. На первый взгляд эти цифры кажутся простыми, но из-за человеческого фактора они могут быть где-то введены неверно. А если данные документа ввести неверно, то возможны серьёзные последствия.

Теперь, если придумать какую-то формулу для этих цифр, по которой будет высчитываться контрольное число. И всем эту формулу рассказать, то все смогут очень просто проверять правильность этих данных — достаточно просто посмотреть на контрольное число, а не сверять все параметры.

Приведём пример использования контрольного числа. Берём заданную дату рождения 090880, дату выдачи 250515 и номер органа 475. Если умножить каждое число, допустим, на 5, то получаем: дата рождения 045040400, дата выдачи 1025025525, и номер органа 203525. А теперь, если сложить полученные произведения, то имеем 45 040 400 + 1 025 025 525 + 203 525 = 1 070 269 450. И делим это число, например, на 800, результат будет 1 337 836,8125. И условимся, что контрольным числом будет то, что остаётся после запятой, после указанных вычислений. Получается 8125.

Кто будет это всё считать?

Конечно же, это делается не вручную, а с помощью специальной программы, которая имеется везде, где требуется проверка документов (например, в паспортом столе, в банке, на таможне). Поэтому нижняя строка паспорта называется машиночитаемой строкой — компьютер видит номера, высчитывает их по заранее заданной известной формуле. Получает контрольное число, и сравнивает его с тем, что написано в документе. На всё уходит меньше секунды. Надеюсь значение последних 2 цифр в паспорте внизу после галочки больше не будут вводить вас в заблуждение.

Это машиночитаемая строка и контрольное число в конце.

Контрольное число помогает, если ошибка в документе была случайной. Но от злонамеренных подделок документа это не спасает.

Подробнее о машиночитаемой строке внизу паспорта вы можете узнать в этом видео.

Формула расчёта контрольного числа паспорта

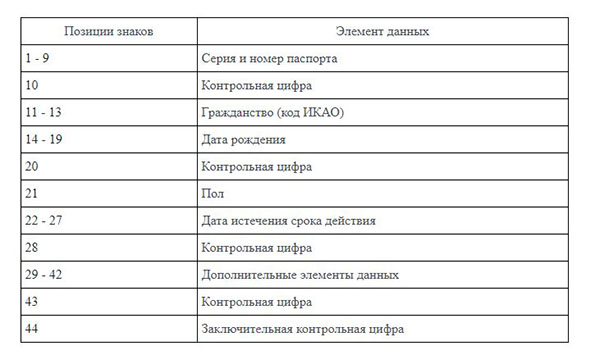
Выше был приведён пример того, как может высчитываться контрольное число и последние 2 цифры в паспорте. Это был простой пример для того, чтобы стала понятна технология. Однако эта цифра в паспорте определяется более сложной формулой и включает в себя больше параметров, чем было представлено в нашем примере. Так, формула контрольного числа паспорта использует такие данные:

Кроме этого, в формуле применяются несколько контрольных чисел, которые высчитываются из некоторых из описанных данных, а затем из них уже определяется итоговое контрольное число, которое и записывается в нижней строке номера паспорта после символа меньше «

Формулу расчёта контрольного числа паспорта регулирует Приложение N 8 к Административному регламенту Министерства внутренних дел Российской Федерации по предоставлению государственной услуги по выдаче, замене паспортов гражданина Российской Федерации, удостоверяющих личность гражданина Российской Федерации.

В частности, в документе приводится такой пример расчёта:

Кроме того, в приложении можно познакомиться с более сложным примером:

Источник

Чем отличается цифра от числа

Все знают, что есть цифры и числа. Но если спросить: «Чем отличается цифра от числа?«, то многие дети, а порой и взрослые, затрудняются с ответом. А как объяснить эту разницу ребенку простыми словами?

Чтобы ответить на этот вопрос и понять в чём различие между цифрой и числом надо разобраться с понятиями, что такое цифра и что такое число.

Числа и цифры: в чем разница

Содержание

Что такое цифра?

Цифра — это письменный знак, изображающий число.

Что значит слово цифра? Это слово арабского происхождения и означает ноль или пустое место. Их существует только десять. Они придуманы для обозначения числа. Цифр всего 10.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Что такое число?

Число — это основное математическое понятие.

Его используют для:

Числа записываются при помощи цифр. Различают несколько видов чисел.

В древнейшие времена цифры обозначали прямолинейными пометками. Палочки до сих пор используются для обозначения римских цифр. Римских цифр 7.

I, V, X, L, C, D, M

Римские числа также, как и арабские, образуются при помощи цифр, только в данном случае римских.

В римских числах желательно разбираться, т.к. они часто используются не только в школьном курсе математики, но и в жизни. Например, на циферблате часов.

Отличия числа от цифры

Надеюсь, что теперь вам всё понятно, и вы сможете без труда объяснить даже ребёнку, чем отличается число от цифры.

На уроках математики в начальной школе используется очень полезное упражнение. Детей просят дать характеристику числу. Другими словами рассказать о числе все, что знаешь. Не всем детям это задание даётся легко. Чтобы его выполнить пригодятся вышеописанные знания и не только.

Какие виды чисел изучаются в начальной школе?

В начальной школе рассматриваются: натуральные числа, число 0, доли и дроби.

Натуральные числа — используются для счёта предметов;

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…

Однозначные числа — состоят из одной цифры;

1, 2, 3, 4, 5, 6, 7, 8, 9

Двузначные числа — состоят из двух цифр;

10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 … 99

Соответственно самое маленькое двузначное число 10, а самое большое — 99.

Аналогично числа можно охарактеризовать как трёхзначные, четырёхзначные и т.д.

Иногда дети затрудняются назвать самое маленькое, например, пятизначное число (10 000) или самое большое семизначное (9 999 999). Просто полезно будет потренироваться это делать.

Чётные — числа, которые делятся пополам без остатка или же заканчиваются на 0, 2, 4, 6, 8;

2, 4, 6, 8, 10, 12, 14…

Нечетные — числа, которые не делятся на 2 без остатка;

1, 3, 5, 7, 9, 11, 13…

Круглые — числа, которые заканчиваются нулём.

10, 20, 30, 40, 50…

Как дать характеристику числу?

Разберём несколько примеров.

Число 7 — однозначное, нечетное, соседи числа 7 числа 6 и 8.

Также чисел первого десятка можно добавить такое дополнительное задание, как состав числа. Т.е. число 7 можно получить сложением чисел 1 и 6, 2 и 5, 3 и 4.

Число 10 — двузначное, чётное, круглое, соседи числа 9 и 11. Число 10 можно получить сложением чисел 1 и 9, 2 и 8, 3 и 7, 4 и 6, 5 и 5.

Чем крупнее число, тем больше можно о нём рассказать.

Число 999 — наибольшее трёхзначное число, нечётное, соседи 998 и 1000, в числе 9 сотен, 9 десятков и 9 единиц.

Надеюсь, что полученные знания были вам полезны и теперь вы знаете чем отличается цифра от числа, сможете объяснить это ребёнку простыми словами, а также потренироваться давать характеристику числам.

С уважением, Ольга Наумова

Заходите в Книжную лавку за полезными книгами!

Благодарю, что поделились статьей в социальных сетях!

Источник