Что значит перпендикулярные углы

Что значит перпендикулярные углы

Углы бывают острые, прямые и тупые.

Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.

Два угла с одной общей стороной называются смежными.

На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.

Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°

При пересечении двух прямых образуются четыре угла:

Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.

∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4

То же справедливо и для ∡1 и ∡3.

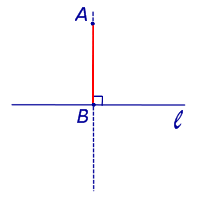
Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.

Перпендикулярность прямых принято обозначать так: a⟂b

Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!

Теорема о перпендикулярных прямых

Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.

Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.

Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.

Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.

Свойство перпендикулярных прямых

Две прямые, перпендикулярные третьей, не пересекаются.

Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.

У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Попробовать бесплатно

Интересное по рубрике

Найдите необходимую статью по тегам

Подпишитесь на нашу рассылку

Мы в инстаграм

Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Посмотреть

Рекомендуем прочитать

Реальный опыт семейного обучения

Звонок по России бесплатный

Посмотреть на карте

Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.

Источник

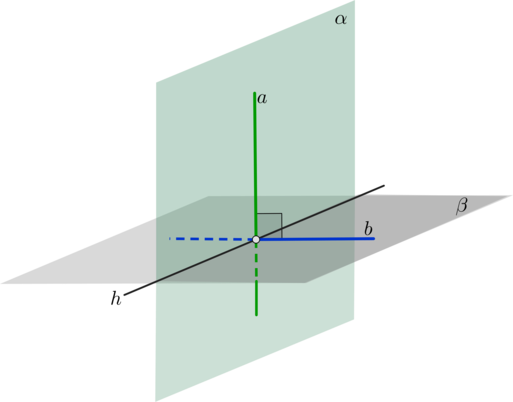
Перпендикулярность. Углы и расстояния в пространстве

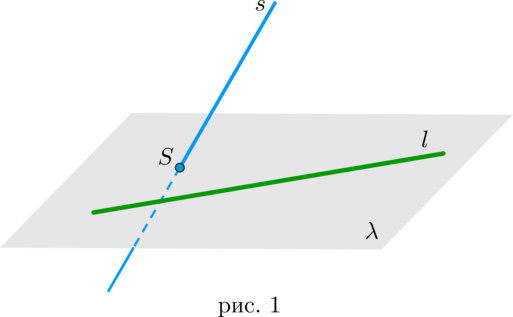
Заметим, что если две прямые лежат в одной плоскости, то, как и в планиметрии, они могут либо пересекаться, либо быть параллельны, либо совпадать. Значит, и угол между такими прямыми ищется так же, как и в планиметрии (напомним, что угол между параллельными прямыми считается равным \(0^\circ\) ). А если через две прямые нельзя провести одну плоскость?

Поэтому к трем видам взаимного расположения прямых в плоскости (пересекаются, параллелельны или совпадают) в пространстве добавляется еще один вид: скрещивающиеся прямые.

Определение

Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.

Теорема 1: признак скрещивающихся прямых

Доказательство

Теорема 2

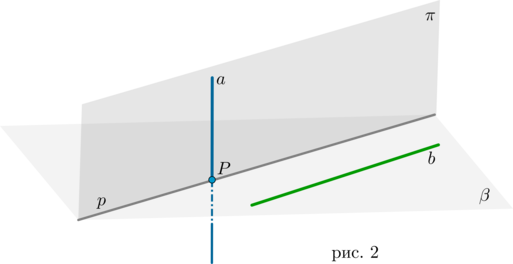
Через каждую из двух скрещивающихся прямых проходит единственная плоскость, параллельная другой прямой (рис. 2).

Доказательство

Определение

Угол между скрещивающимися прямыми – это угол между пересекающимися прямыми, соответственно параллельными двум скрещивающимся прямым.

Таким образом, можно определить следующий алгоритм нахождения угла между скрещивающимися прямыми (рис. 2):

Шаг 1. Через одну из двух скрещивающихся прямых \(a\) провести плоскость \(\pi\) параллельно другой прямой \(b\) (по алгоритму, приведенному в теореме 2);

Определение

Таким образом, перпендикулярными могут быть как и пересекающиеся прямые (лежащие в одной плоскости), так и скрещивающиеся прямые (не лежащие в одной плоскости).

Утверждение 1

Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и вторая прямая перпендикулярна этой прямой:

\[a\parallel b, \ a\perp c \Longrightarrow b\perp c\]

Утверждение 2

Две прямые, перпендикулярные третьей прямой, не пересекаются (то есть либо параллельны, либо скрещиваются):

\[a\perp c, \ b\perp c \Longrightarrow a\cap b=\varnothing\]

Определение

Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.

Следствие 1

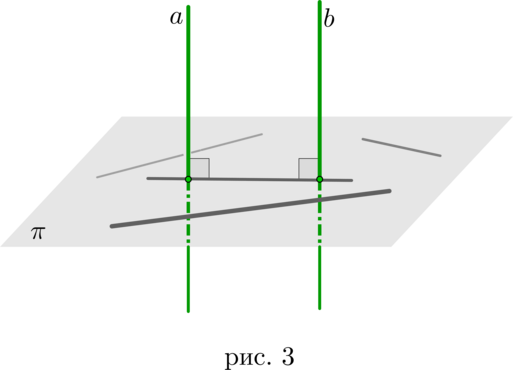
Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости (рис. 3).

(Данное утверждение напрямую следует из утверждения 1.)

Верно и обратное утверждение:

Следствие 2

Если две прямые перпендикулярны плоскости, то они параллельны (рис. 3).

Теорема 3: признак перпендикулярности прямой и плоскости

Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.

Доказательство

Следствие 3

Через любую точку пространства можно провести плоскость, перпендикулярную данной прямой, и притом только одну.

Следствие 4

Через любую точку пространства проходит прямая, перпендикулярная данной плоскости, и притом только одна.

Определение

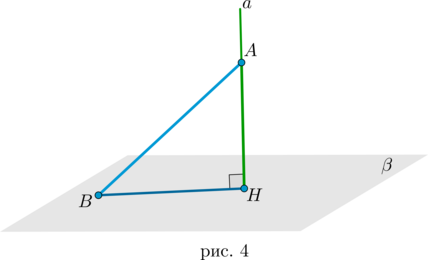
Расстояние от точки до плоскости

Длина перпендикуляра \(AH\) к плоскости \(\beta\) равна расстоянию от точки \(A\) до плоскости \(\beta\) (рис. 4).

Расстояние между параллельными плоскостями

Для того, чтобы найти расстояние между параллельными плоскостями, нужно из любой точки одной плоскости опустить перпендикуляр к другой плоскости. Длина этого перпендикуляра и есть расстояние между параллельными плоскостями.

Заметим, что расстояние между пересекающимися плоскостями равно нулю.

Расстояние между скрещивающимися прямыми

Для того, чтобы найти расстояние между скрещивающимися прямыми, удобно найти расстояние между одной из них и плоскостью, проходящей через вторую прямую параллельно первой.

Доказательство

2. Случай, когда из перпендикулярности проекции следует перпендикулярность наклонной, доказывается аналогично.

Замечание

Данная теорема является очень важным и незаменимым инструментов во многих задачах стереометрии.

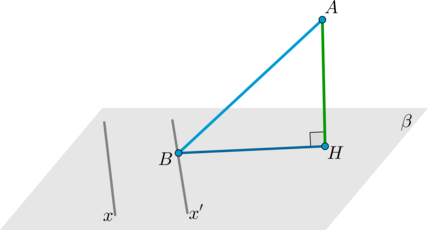
Определение

Замечание

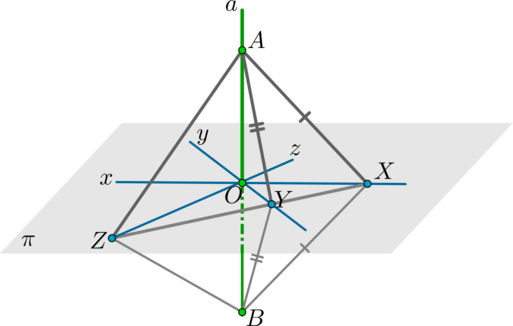
Таким образом, чтобы найти угол между наклонной прямой и плоскостью, необходимо отметить некоторую точку \(A\) на этой прямой и провести перпендикуляр \(AH\) к плоскости. Если \(B\) – точка пересечения прямой с плоскостью, то \(\angle ABH\) и есть искомый угол (рис. 4).

Определение

Замечание

Прямая \(a\) в данном случае является аналогом вершины плоского угла, а полуплоскости – аналогом сторон плоского угла.

Таким образом, при пересечении двух плоскостей образуется четыре двугранных угла.

Определение

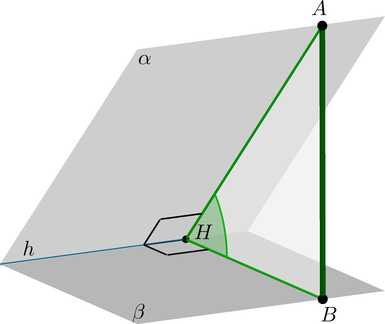
Если к ребру \(a\) двугранного угла провести перпендикулярную плоскость (через любую точку), то она пересечет грани двугранного угла по лучам. Угол, образованный данными лучами, называется линейным углом данного двугранного угла.

Замечание

Таким образом, при пересечении двух плоскостей образуется четыре двугранных угла, которым соответствуют четыре линейных угла.

Определение

Теорема 4: признак перпендикулярности плоскостей

Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.

Доказательство

Источник

Углы на плоскости

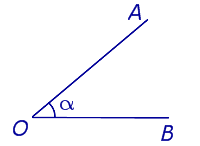
Схему обозначения углов рассмотрим на примере угла, изображенного на рисунке 1.

Изображенный на рисунке 1 угол можно обозначить тремя способами:

Углы называют равными углами, если их можно совместить.

Углом в 1° (один градус) называют угол, составляющий одну девяностую часть прямого угла.

Таблица 1 – Типы углов в зависимости от величины в градусах

Прямой угол равен 90°

Острый угол

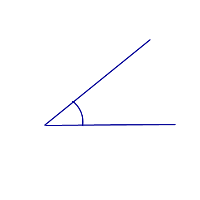
Острый угол меньше 90°

Тупой угол

Развернутый угол

Развернутый угол равен 180°

Угол больший, чем развернутый

Полный угол

Полный угол равен 360°

Угол, равный нулю

Такой угол равен 0°

Таблица 2 – Типы углов в зависимости расположения сторон

Свойство вертикальных углов:

Вертикальные углы равны

Смежные углы

Свойство смежных углов:

Сумма смежных углов равна 180°

Углы с соответственно параллельными сторонами

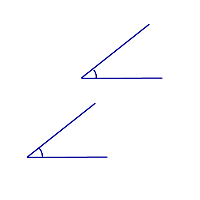
Свойство углов с соответственно параллельными сторонами:

Углы с соответственно параллельными сторонами равны, если оба являются острыми или оба являются тупыми

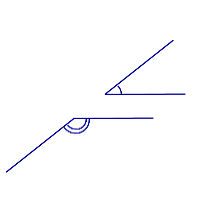
Свойство углов с соответственно параллельными сторонами:

Углы с соответственно перпендикулярными сторонами

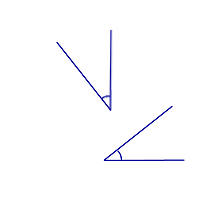
Свойство углов с соответственно перпендикулярными сторонами:

Углы с соответственно перпендикулярными сторонами равны, если оба являются острыми или оба являются тупыми

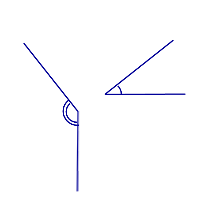
Свойство углов с соответственно перпендикулярными сторонами:

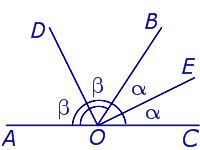
На этом рисунке углы AOB и BOC – смежные, а лучи OE и OD – биссектрисы этих углов. Поскольку

Источник

Вертикальные и перпендекулярные углы

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Урок математики в 6-м классе по теме «Вертикальные углы. Перпендикулярные прямые»

Тип урока: изучение нового материала.

Цели: ввести определение перпендикулярных прямых, перпендикулярных отрезков (лучей).

Научить строить перпендикулярные прямые;

Развивать навыки построения геометрических фигур;

Развивать логическое мышление.

Научить распознавать вертикальные углы.

Приобретаемые навыки детей: построение перпендикулярных прямых, распознавать вертикальные углы.

Формы организации работы детей: индивидуальная и фронтальная работа.

Используемое оборудование: 1ПК, интерактивная доска.

I. Организационный момент.

– Проверьте все ли готово у вас к уроку: дневник, учебник, тетрадь, ручка, линейка, чертежный треугольник, цветные карандаши.

II. Сообщение темы урока и цели.

– Изучая геометрические фигуры, вы уже не раз встречались с перпендикулярными прямыми. Например, смежные стороны прямоугольника перпендикулярны. Как убедиться в том, что две линии (прямые) перпендикулярны? С древних пор строители проверяли перпендикулярность стены основанию дома с помощью отвеса, то есть грузика на веревке. Отсюда и произошло название перпендикуляра: латинское “перпендикулярис” означает “отвесной”. Чтобы построить перпендикуляр к прямой, достаточно построить прямой угол. Это вы умеете делать с помощью чертежного треугольника и с помощью транспортира.

V. Изучение нового материала.

– Итак, давайте выясним, какие прямые называют перпендикулярными.

– Прямые АВ и MN пересекаются, но не образуют 4 прямых угла.

Прямые CD и MN пересекаются и образуют 4 прямых угла.

– Такие прямые называются перпендикулярными.

В математике слово “перпендикулярные” обозначают знаком .

Если при пересечении двух прямых образуется один прямой угол, то и три остальных угла тоже будут прямыми.

– Вы узнали, какие прямые называются перпендикулярными. Пришло время научиться стоить перпендикулярные прямые. И начнем мы с построение перпендикулярной прямой через точку, лежащую на данной прямой.

– Сядьте равно. Руки положите за спины. Не поворачивая головы, посмотрите на окно, на стенд на противоположной стороне, наверх, на парту, на доску. Закройте глаза, представьте голубое небо. Откройте глаза. Руки положите на стол. Продолжим…

VII. Изучение нового материала.

– Теперь самостоятельно попробуйте построить две перпендикулярные прямые через точку не лежащую на данной прямой.

– Проверим ваш алгоритм построения:

Строим произвольную прямую.

Отмечаем точку вне прямой.

Прикладываем чертежный треугольник.

– Ребята, попробуйте провести через эту же точку еще одну перпендикулярную прямую. Получилось? Какой вывод можно сделать? Правильно: через любую точку плоскости можно провести единственную прямую, перпендикулярную данной .

VIII. Закрепление нового материала.

– Пришла пора применить полученные знания при решении геометрических задач: “В треугольнике АВМ угол А – прямой. Установите, перпендикулярны ли прямые:

– А есть ли другой способ определить, перпендикулярны ли прямые? (Обязательно найдется ученик, который по названию угла определит нужные прямые, если нет, то стоит детей подвести к этой простой версии.)

– Конечно же, многие задачи можно решить устно путем логических рассуждений, не делая чертежи. Давайте попробуем:

IX. Дополнительное задание

X. Подведение итогов.

– Какие прямые называют перпендикулярными? Какие отрезки и какие лучи называют перпендикулярными? С помощью каких чертежных инструментов строят перпендикулярные прямые?

Источник

Углы, стороны которых соответственно перпендикулярны

Теорема об углах с соответственно перпендикулярными сторонами

поэтому ∠O + ∠O₁ = 180°

Сторона ОА перпендикулярна стороне О₁А₁, сторона ОВ перпендикулярна стороне О₁В₁,

Углы, стороны которых соответственно перпендикулярны

Доказательство теоремы

Шаг 1

Если угол АОВ развернутый, то угол А₁О₁В₁ также будет развернутым.

Это следует из того, что через точку (О₁) к прямой (развернутый угол АОВ и будет прямой) можно провести только один перпендикуляр. Следовательно, перпендикуляры О₁В₁ и О₁А₁ совпадут, т.е. будут лежать на одной прямой. А это означает, что образованный угол будет развернутым.

Доказательство теоремы об углах, стороны которых соответственно перпендикулярны. Шаг 1

Шаг 2

Рассмотрим случай, когда угол АОВ прямой, следовательно, ОВ⊥ОА.

Итак, ОВ⊥ОА и О₁А₁⊥ ОА (две прямые перпендикулярны третьей), следовательно, эти перпендикулярные прямые будут параллельны друг другу:

Теперь рассмотрим две параллельные прямые ОВ и О₁А₁ и секущую их О₁В₁.

По свойству углов, образованных параллельными прямыми и секущей, сумма односторонних углов будет равна 180 градусов. Следовательно:

По условию ОВ⊥ О₁В₁, следовательно, угол 1 равен 90 градусов, тогда получим:

В результате получили:

Доказательство теоремы об углах, стороны которых соответственно перпендикулярны. Шаг 2

Источник