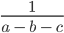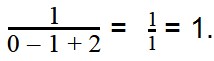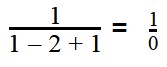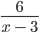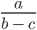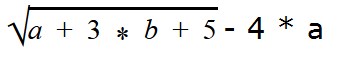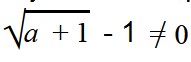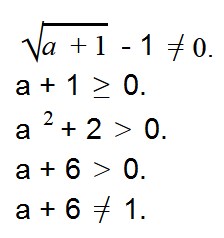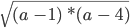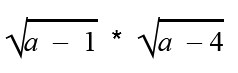Что значит переменная имеет смысл

Область допустимых значений (ОДЗ): теория, примеры, решения

Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.

В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.

Допустимые и недопустимые значения переменных

Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.

Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.

Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.

Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.

То есть отсюда следует полное определение

Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.

Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.

Что такое ОДЗ?

Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.

Область ОДЗ – это множество значений, допустимых для данного выражения.

Рассмотрим на примере выражения.

Как найти ОДЗ? Примеры, решения

Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.

Существуют выражения, где их вычисление невозможно:

Все это говорит о том, как важно наличие ОДЗ.

Найти ОДЗ выражения x 3 + 2 · x · y − 4 .

Решение

В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.

Ответ: x и y – любые значения.

Решение

Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.

Решение

Решение

Почему важно учитывать ОДЗ при проведении преобразований?

При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.

Рассмотрим на примере.

Рассмотрим пример с наличием подкоренного выражения.

Нужно избегать преобразований, которые сужают ОДЗ.

Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.

Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.

При наличии логарифмов дело обстоит немного иначе.

При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.

Источник

Значение числового, буквенного выражения и выражения с переменными

В процессе разбора тем о числовых, буквенных выражениях и выражениях с переменными следует обратить внимание на понятие значение выражения. Ниже дадим определение этому термину, рассмотрим примеры.

Что такое значение числового выражения

Мы знакомимся с числовыми выражениями с самого начала школьного обучения. Да и почти сразу начинает использоваться понятие «значение числового выражения». Так обозначают выражения, составляющие которого – числа, соединяемые знаками арифметических действий: плюс, минус, умножить, разделить.

Значение числового выражения – это конечное число, получаемое в результате выполнения заданных действий в исходном числовом выражении.

Зачастую в словосочетании «значение числового выражения» слово «числовое» не употребляют, поскольку в любом случае понятно, значение какого выражения рассматривается.

В основном интерес вызывает не само числовое выражение, а его значение. Практически всегда существует задача по нахождению значения заданного выражения, которая так и обозначается: «найти значение выражения». В соответствующей статье можно детально изучить сам процесс нахождения значения числовых выражения разного рода с примерами.

Значение буквенного выражения и выражения с переменными

Кроме числовых, интерес представляют и буквенные выражения – те выражения, составляющими которого являются, в том числе, одна или несколько букв. Буквы в буквенном выражении обозначают разные числа, и при замене букв на числа получается числовое выражение.

Значения букв – числа, которые заменяют эти буквы в буквенном выражении. Тогда значение буквенного выражения при заданных значениях букв – это значение полученного числового выражения.

Таким образом, речь идет не о значении буквенного выражения, как такового, а о его значении, когда заданы (определены) конкретные значения букв.

В программе алгебры буквы в буквенном выражении могут принимать разнообразные значения, тогда буквы называют переменными, а буквенные выражения – выражениями с переменными. Логично следует введение понятия значения выражений при выбранных значениях переменных.

Значение выражения с переменными при выбранных значениях переменных – это значение числового выражения, полученное при подстановке конкретных выбранных значений переменных в заданное выражение.

Возможен вариант, когда выбранные переменные –различны, а значение исходного выражения при этих переменных одинаково.

Значения переменных возможно задать из областей допустимых значений, которые им соответствуют, поскольку в ином случае, подставив значения, не принадлежащие области допустимых значений, можно получить числовое выражение, не имеющее смысла.

Источник

Функция. Зависимые и независимые переменные. Область определения и область значений функции.

теория по математике 📈 функции

Определение понятия функции. Переменные.

Зависимость переменной у от переменной х, при которой любому значению переменной х соответствует единственное значение переменной у, называют функцией.

Ключевое слово, которое нужно запомнить в определении функции – это зависимость.

Например, человек идет на деловую встречу, но чувствует, что он опаздывает. Он ускоряет свой шаг, потому что от его скорости зависит время. Чем быстрее он двигается, тем меньше времени уйдет у него на дорогу. То есть время зависит от скорости.

Или, например, спортсмен метает ядро на дальнее расстояние. Чем сильнее будет бросок, тем дальше полетит ядро. Скорость полета зависит от силы толчка. Здесь опять прослеживается зависимость.

Например, функция задана формулой у = – 3х 2 – 7. Равносильная ей запись такая: f(x)= – 3х 2 – 7.

Области определения и значения функции

Все возможные значения независимой переменной (х) называют областью определения функции.

Все значения, которые принимает зависимая переменная (у) называют областью значений функции.

Если какая-либо функция у=f(x) задана формулой, а при этом ее область определения не указана, то считается, что она состоит из любых значений переменной, при которых выражение имеет смысл.

Области определения и значений школьных функций

1. Для линейной функции областью определения будет являться любое число.

Если у такой функции k≠0, то областью ее значений также будет являться любое число.

При k=0 область значений этой функции состоит из единственного числа b.

Например, функция задана формулой у = 7. Тогда ее область значения — это число 7, а область определения – любое число.

2. Гипербола задается формулой вида y = k/x.

Область определения такой функции – любое число, кроме нуля.

Область значений такой функции – аналогичная.

3. Функция, заданная формулой y= |x|, имеет область определения – любое число.

4. У функций у = х 2 и у = х 3 область определения – любое число.

Для того чтобы понимать, как находится область определения функции и рассмотреть примеры заданий на нахождение области определения функции, вспомним правила, при которых существуют ограничения и выражение не имеет смысл: нельзя делить на нуль; нельзя извлекать квадратный корень из отрицательного числа.

Пример 3. Рассмотрим, как находится область определения функций, которые заданы следующими формулами:

В знаменателе этого выражения содержится переменная х, поэтому надо проверить, при каком значении он может быть равным нулю и исключить это значение из области определения, так как на знаменатель делят, а на нуль делить нельзя.

Итак, имеем знаменатель х + 11. Приравниваем его к нулю, получаем х + 11 = 0. Решаем простое уравнение на нахождение неизвестного слагаемого и получаем х= – 11. Это число исключаем из области определения функции.

Ответ: (1) и (2) – множество всех чисел; (3) – любое число, кроме (-11) или х ≠ – 11; (4) х ≥0.

Источник

Область допустимых значений функции

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Допустимые и недопустимые значения переменных

В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.

Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.

Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.

Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.

Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.

Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.

Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.

Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.

Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.

Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.

Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.

В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.

Пример 1

Рассмотрим выражение

В выражении три переменные (a, b, c).

Запишем значения переменных в виде: a = 1, b = 1, c = 2.

Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:

Таким же образом можем выяснить, какие значения переменных — недопустимые.

Подставим значения переменных в выражение

На ноль делить нельзя.

Что такое ОДЗ

ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».

Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.

Пример 2

Рассмотрим выражение

Пример 3
Рассмотрим выражение

ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.

Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.

Как найти ОДЗ: примеры решения

Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.

Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.

Мы не можем вычислить значение выражения, если:

Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.

Давайте потренируемся находить ОДЗ.

Пример 4

Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.

В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.

ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.

Ответ: (a и b), где a — любое число и b — любое число.

Пример 5

Найдем область допустимых значений (ОДЗ) переменной выражения

Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.

Это значит, что мы может сказать, что ОДЗ переменной a в выражении 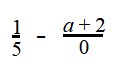— пустое множество.

Пустое множество изображается в виде вот такого символа Ø.

Пример 6

Найдем область допустимых значений (ОДЗ) переменных в выражении

Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.

Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.

Пример 7

Найдем ОДЗ переменной a в выражении

Прежде всего, нам нужно подобрать такое условие, при котором в знаменателе дроби не будет ноля —

Мы знаем, что выражение под знаком корня должно быть положительным. Это дает нам второе условие: a + 1 ≥ 0.

Мы не можем вычислить логарифм отрицательного выражения. Получаем третье условие: a 2 + 2 > 0.

Выражении в основании логарифма не должно быть отрицательным и не должно равняться единице. Получаем условие 4: a + 6 > 0.

Как видите, записывая ОДЗ, мы ставим квадратные и круглые скобки.

Запомните

Например, если х > 6, но х

Зачем учитывать ОДЗ при преобразовании выражения

Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.

Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.

Тождественное преобразование может:

Рассмотрим каждый случай в отдельности.

Пример 8

Поскольку мы должны следить за тем, чтобы в выражении не возникало деление ноль, определяем условие a ≠ 0.

Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).

В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.

ОДЗ для a — это R — множество всех вещественных чисел.

Преобразование расширило ОДЗ — добавился ноль.

Пример 9

Рассмотрим выражение a 2 + a + 4 * a

ОДЗ a для этого выражения — множество R.

В выражении есть подобные слагаемые, выполним тождественное преобразование.

После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a

ОДЗ переменной a для этого выражения — множество R.

Это значит, что тождественное преобразование никак не повлияло на ОДЗ.

Пример 10

Рассмотрим выражение

Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).

Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.

Приведем выражение к виду

Решив систему линейных неравенств, получаем множество [4; + ∞).

Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).

Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.

Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.

Источник

Переменная. Зачем нужны переменные?

Переменная – величина, имеющая неизвестное либо переменное (отсюда и название) значение.

Примеры применения переменной:

Зачем нужны переменные?

Как уже говорилось выше, переменные служат для записи изменяемых или пока что неизвестных значений. Например, представьте, что вам нужно попасть на дачу, которая находиться в \(50\) километрах от вашего дома. Вопрос – как быстро вы это расстояние преодолеете?

Ответ: это смотря с какой скоростью мы будем двигаться! Если пешком (скорость \(5\) км/ч), то за \(\frac<50><5>\) \(=10\) часов. Если на велосипеде (скорость \(10\) км/ч), то за \(\frac<50><10>\) \(=5\) часов. А если на машине (скорость \(50\) км/ч), то за \(\frac<50><50>\) \(=1\) час.

Значение переменной и значение выражения

Значением переменной называют то конкретное число, которое подставляют вместо буквы.

Например, пусть у нас есть выражение \(3a^<2>\) содержащее переменную \(a\). Если мы возьмем значением переменной \(a\) число \(2\), то значение этого выражения будет \(3a^<2>=3\cdot2^<2>=3\cdot4=12\). Если же мы примем \(a=7\), то \(3a^<2>\) станет равно \(3\cdot7^<2>=3\cdot49=147\). И так далее.

Источник