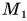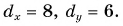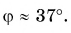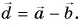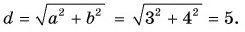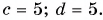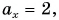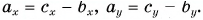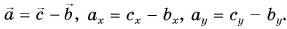Что значит определить проекцию
Содержание:
Проекция вектора на ось:
Вы уже знаете, что вектор имеет модуль и направление. При решении задач часто используется понятие проекция вектора на ось. Что такое проекция вектора? Как ее определяют?
Начнем с понятия проекция точки на ось.
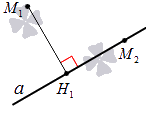
Проекция точки — это основание перпендикуляра, опущенного из данной точки на ось.
На рисунке 24 точка
Как определяют проекцию вектора на ось
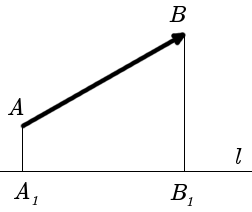
Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.
На рисунке 25 проекция вектора 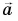
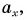
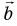
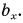
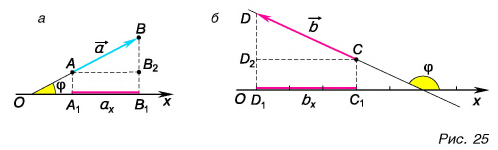
Проекция 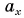
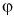
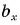
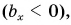
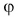
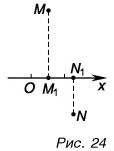
А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).
Проекцию вектора можно выразить через его модуль и угол между вектором и осью.
Рассмотрим треугольник 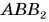
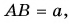
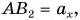
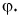
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.
Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.
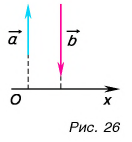
Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось.
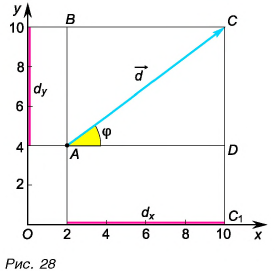
С помощью рисунка 27, а, б убедитесь, что из векторного равенства 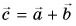
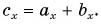
Можно ли найти модуль и направление вектора по его проекциям на координатные оси
Рассмотрим вектор 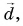
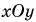
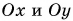
Модуль вектора 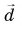
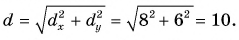
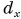
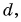
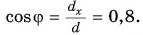
Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.
Вектор в пространстве определяется тремя проекциями: 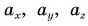
Главные выводы:
Пример №1
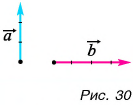
1. Определите сумму и разность взаимно перпендикулярных векторов 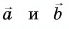
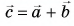
Решение
Сумму векторов 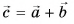
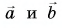
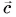
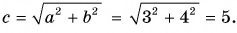
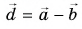
Модуль вектора 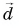
Ответ:
Пример №2
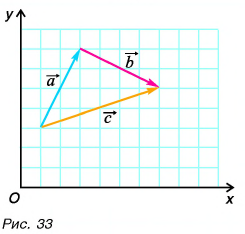
Выразите вектор 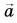
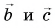
Решение
По правилу треугольника находим: 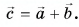
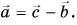
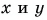
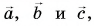
Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы:
Ответ:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Проекция точки на прямую, координаты проекции точки на прямую
Данная статья рассматривает понятие проекции точки на прямую (ось). Мы дадим ему определение с использованием поясняющего рисунка; изучим способ определения координат проекции точки на прямую (на плоскости или в трехмерном пространстве); разберем примеры.
Проекция точки на прямую, определение
В статье «Проекция точки на плоскость, координаты» мы упоминали, что проецирование фигуры является обобщенным понятием перпендикулярного или ортогонального проецирования.
Все геометрические фигуры состоят из точек, соответственно проекция этой фигуры есть множество проекций всех ее точек. Поэтому, чтобы иметь возможность спроецировать фигуру на прямую, необходимо получить навык проецирования точки на прямую.
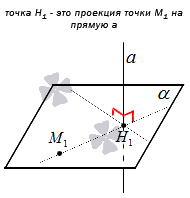
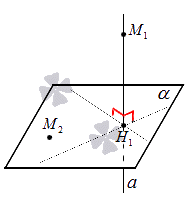
Проекция точки на прямую – это или сама точка, если она принадлежит заданной прямой, или основание перпендикуляра, опущенного из этой точки на заданную прямую.
Данное определение верно для случая на плоскости и в трехмерном пространстве.
Нахождение координат проекции точки на прямую
Рассмотрим данный вопрос в случаях проецирования на плоскости и в трехмерном пространстве.
— составляем уравнение прямой (если оно не задано). Для совершения этого действия необходим навык составления основных уравнений на плоскости;
— записываем уравнение прямой b (проходящей через точку М 1 и перпендикулярной прямой a ). Здесь поможет статья об уравнении прямой, проходящей через заданную точку перпендикулярно заданной прямой;
Решение
Составим систему уравнений из общих уравнений прямых a и b и решим ее:
Подробнее рассмотрим случай, когда необходимо определить координаты проекции заданной точки на координатные прямые и параллельные им прямые.
Решение
— запишем уравнение прямой а (если оно не задано). Для решения этой задачи необходимо ознакомиться со статьей об уравнениях прямой в пространстве;
Решение
Теперь найдем координаты точки пересечения прямой а и плоскости α, для этого используем два способа:
В данном случае используем метод Крамера, но возможно применить любой удобный:
Вычислим искомые координаты точки пересечения прямой a и плоскости α по параметрическим уравнениям прямой a при λ = 1 :
Проекция точки на плоскость, координаты проекции точки на плоскость
В этой статье мы найдем ответы на вопросы о том, как создать проекцию точки на плоскость и как определить координаты этой проекции. Опираться в теоретической части будем на понятие проецирования. Дадим определения терминам, сопроводим информацию иллюстрациями. Закрепим полученные знания при решении примеров.
Проецирование, виды проецирования
Для удобства рассмотрения пространственных фигур используют чертежи с изображением этих фигур.
Проекция фигуры на плоскость – чертеж пространственной фигуры.
Очевидно, что для построения проекции существует ряд используемых правил.
Проецирование – процесс построения чертежа пространственной фигуры на плоскости с использованием правил построения.
Использование тех или иных правил определяет тип проецирования: центральное или параллельное.
Частным случаем параллельного проецирования является перпендикулярное проецирование или ортогональное: в геометрии в основном используют именно его. По этой причине в речи само прилагательное «перпендикулярное» часто опускают: в геометрии говорят просто «проекция фигуры» и подразумевают под этим построение проекции методом перпендикулярного проецирования. В частных случаях, конечно, может быть оговорено иное.
Отметим тот факт, что проекция фигуры на плоскость по сути есть проекция всех точек этой фигуры. Поэтому, чтобы иметь возможность изучать пространственную фигуру на чертеже, необходимо получить базовый навык проецировать точку на плоскость. О чем и будем говорить ниже.
Проекция точки на плоскость
Напомним, что чаще всего в геометрии, говоря о проекции на плоскость, имеют в виду применение перпендикулярной проекции.
Произведем построения, которые дадут нам возможность получить определение проекции точки на плоскость.
Проекция точки на плоскость – это либо сама точка (если она принадлежит заданной плоскости), либо основание перпендикуляра, опущенного из заданной точки на заданную плоскость.
Нахождение координат проекции точки на плоскость, примеры
Решение очевидным образом следует из данного выше определения проекции точки на плоскость.
Таким образом, для нахождения координат проекции точки на плоскость необходимо:
— получить уравнение плоскости α (в случае, если оно не задано). Здесь вам поможет статья о видах уравнений плоскости;
Рассмотрим теорию на практических примерах.
Решение
Как мы видим, уравнение плоскости нам задано, т.е. составлять его необходимости нет.
Составим систему уравнений:
И решим ее, используя метод Крамера:
Решение
В первую очередь запишем уравнение плоскости, проходящей через три заданные точки:
Далее рассмотрим еще один вариант решения, отличный от того, что мы использовали в первом примере.
Теперь, имея координаты точки прямой М 1 и координаты направляющего вектора этой прямой, запишем параметрические уравнения прямой в пространстве:
Затем определим координаты точки пересечения плоскости х – 2 y + 2 z – 4 = 0 и прямой
Для этого в уравнение плоскости подставим:
Отдельно остановимся на вопросе нахождения координат проекции точки на координатные плоскости и плоскости, которые параллельны координатным плоскостям.
Продемонстрируем, как был получен этот результат.
x = x 1 + λ y = y 1 z = z 1
Решение
Проекция вектора на ось. Проекция вектора на вектор
 |
| рис. 1 |
Формула вычисления проекции вектора на вектор
Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:
Примеры задач на проекцию вектора
Примеры вычисления проекции вектора для плоских задач
Найдем скалярное произведение этих векторов
a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11
Найдем модуль вектора b
| b | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
Найдем проекцию вектора a на вектор b
| Пр b a = | a · b | = | 11 | = 2.2 |
| | b | | 5 |
Примеры вычисления проекции вектора для пространственных задачи
Найдем скалярное произведение этих векторов
a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12
Найдем модуль вектора b
| b | = √ 4 2 + 2 2 + 4 2 = √ 16 + 4 + 16 = √ 36 = 6
Найдем проекцию вектора a на вектор b
| Пр b a = | a · b | = | 12 | = 2 |
| | b | | 6 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Как найти проекцию точки на плоскость: методика определения и пример решения задачи
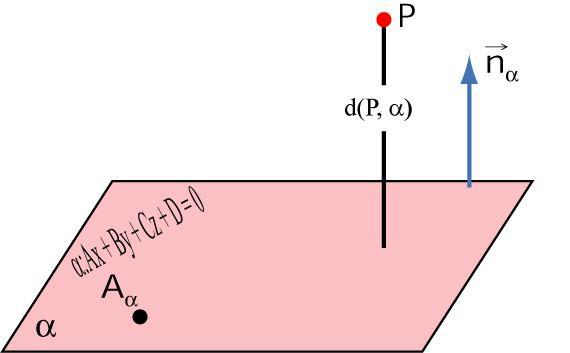
При решении геометрических задач в пространстве часто возникает проблема определения расстояния между плоскостью и точкой. В некоторых случаях это необходимо для комплексного решения. Эту величину можно вычислить, если найти проекцию на плоскость точки. Рассмотрим этот вопрос подробнее в статье.
Уравнение для описания плоскости

Уравнением общего вида, определяющим все точки, которые принадлежат данной плоскости, является следующее:
Далее в статье будем использовать записанное уравнение. Оно требуется, чтобы найти проекцию точки на плоскость.
Понятие о проекции точки и ее вычисление
Предположим, что задана некоторая точка P(x1; y1; z1) и плоскость. Она определена уравнением в общем виде. Если провести перпендикулярную прямую из P к заданной плоскости, то очевидно, что она пересечет последнюю в одной определенной точке Q (x2; y2; z2). Q называется проекцией P на рассматриваемую плоскость. Длина отрезка PQ называется расстоянием от точки P до плоскости. Таким образом, сам PQ является перпендикулярным плоскости.
Как можно найти координаты проекции точки на плоскость? Сделать это не сложно. Для начала следует составить уравнение прямой, которая будет перпендикулярна плоскости. Ей будет принадлежать точка P. Поскольку вектор нормали n¯(A; B; C) этой прямой должен быть параллелен, то уравнение для нее в соответствующей форме запишется так:
(x; y; z) = (x1; y1; z1) + λ*(A; B; C).
После того как записано векторное уравнение для перпендикулярной плоскости линии, необходимо найти общую точку пересечения для рассматриваемых геометрических объектов. Ее координаты и будут проекцией P. Поскольку они должны удовлетворять обоим равенствам (для прямой и для плоскости), то задача сводится к решению соответствующей системы линейных уравнений.
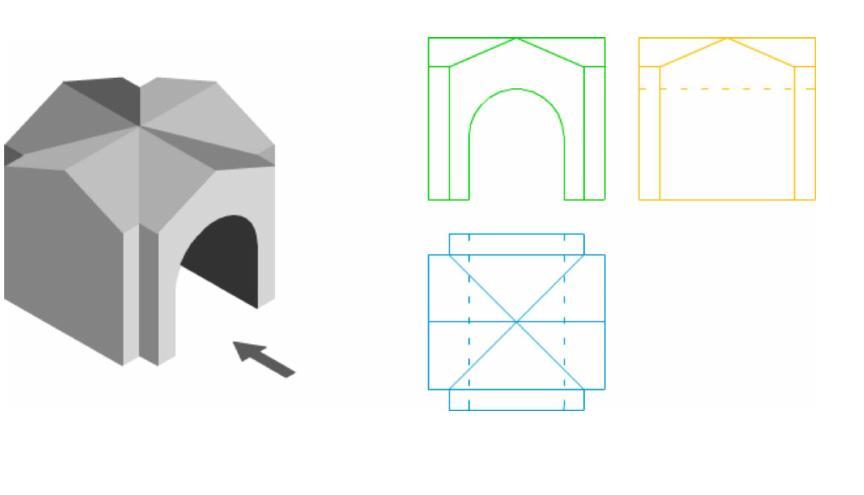
Понятие проекции часто используется при изучении чертежей. На них изображаются боковые и горизонтальные проекции детали на плоскости zy, zx, и xy.
Вычисление расстояния от плоскости до точки
Как выше было отмечено, знание координат проекции на плоскость точки позволяет определить дистанцию между ними. Используя обозначения, введенные в предыдущем пункте, получаем, что искомое расстояние равно длине отрезка PQ. Для его вычисления достаточно найти координаты вектора PQ¯, а затем рассчитать его модуль по известной формуле. Конечное выражение для d расстояния между P точкой и плоскостью принимает вид:
Полученное значение d представлено в единицах, в которых задается текущая декартова координатная система xyz.
Пример задачи
Следует найти точки проекцию на плоскость и вычислить между ними расстояние.
В первую очередь составим уравнение прямой, которая пересекает плоскость под углом 90o. Имеем:
Записывая это равенство в явном виде, приходим к следующей системе уравнений:
Подставляя значения координат из первых трех равенств в четвертое, получим значение λ, определяющее координаты общей точки прямой и плоскости:
Подставим найденный параметр в уравнение прямой и найдем координаты проекции исходной точки на плоскость:
Для вычисления дистанции между заданными в условии задачи геометрическими объектами применим формулу для d:
В данной задаче мы показали, как находить проекцию точки на произвольную плоскость и как вычислять между ними расстояние.