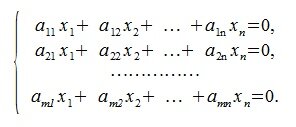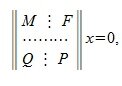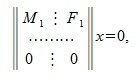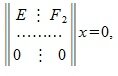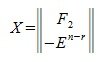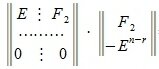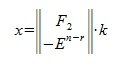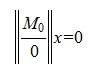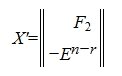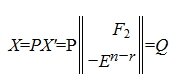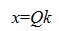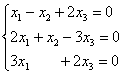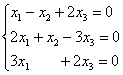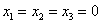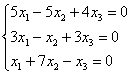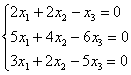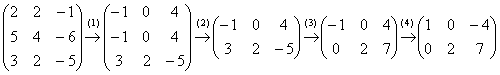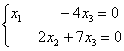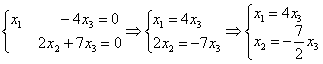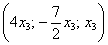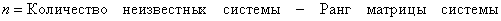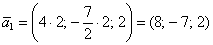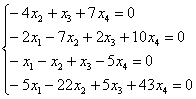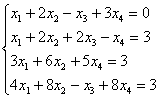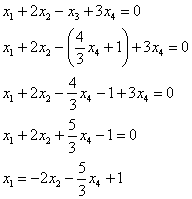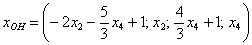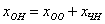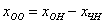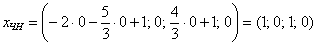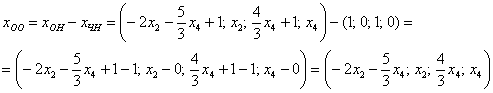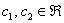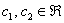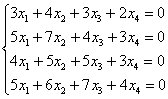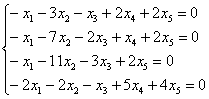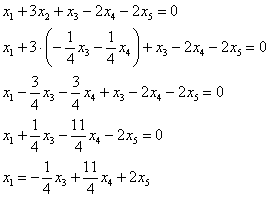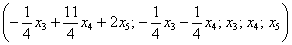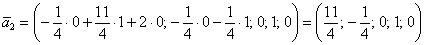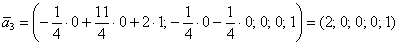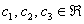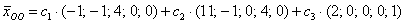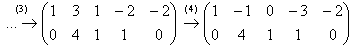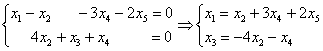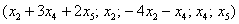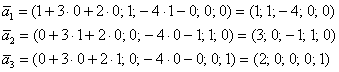Что значит однородная система
Однородная система линейных уравнений
Рассмотрим систему линейных уравнений (СЛУ):
Представим (1) в матричном виде:
СЛУ (1) (или (2)) называется однородной системой линейных уравнений, т.к. правая часть системы равна нулю.
Однородная система линейных уравнений всегда совместна, т.к. вектор 0 всегда является решением системы (1):
Это решение называется нулевым или тривиальным решением.
Если A n×n матрица и rank( A)= n, то нулевой вектор является единственным решением системы (1), в противном случае система имеет множество решений.
Обшее решение однородной системы линейных уравнений
Применяя метод исключения Гаусса для системы (3), получим:
В уравнении (5) вместо x подставляя матрицу (6), получим:
Таким образом, векторы столбцы матрицы X являются решением системы (2) (или (1)). Более того, эти векторы линейно независимы и их линейная комбинация также является решением (2).
Общее решение системы однородных линейных уравнений имеет следующий вид:
Общее решение системы однородных линейных уравнений можно также записать в следующем виде:
Множество всех решений (8)(или (9)) образует ядро или нуль пространство матрицы A и обозначается через Ker (A) или N(A).
Сделаем замену переменных:
Аналогично вышеизложенному векторы столбцы матрицы X’:
образуют множесво всех решений однородной системы линейных уравнений (12).
Учитывая (11) получим:
Общее решение системы однородных линейных уравнений имеет следующий вид:
Общее решение системы однородных линейных уравнений можно также записать в следующем виде:
Нахождение общего решения однородной системы линейных уравнений с помощью псевдообратной матрицы
Если rank(A)= r, r общее решение можно представить в следующем виде:
где E —единичная матрица, A + — псевдообратная к A матрица.
Для проверки подставим (16) в (2):
Ax=A(E−A + A)z=(A−AA + A)z=(A−A)z=0.
Ранг матрицы rank( E−A + A)= n-r. Следовательно столбцы матрицы E−A + A образуют множество всех решений системы (2).
Решение однородной системы линейных уравнений онлайн
Для решения однородной системы линейных уравнений пользуйтесь онлайн калькулятором который решает однородную систему по шагам и находит полное решение.
Однородные системы линейных алгебраических уравнений. Фундаментальная система решений. Первая часть.
Однородные системы линейных алгебраических уравнений. Нулевое (тривиальное) решение.
Однако следствие из теоремы Кронекера-Капелли однозначно указывает на то, что если СЛАУ имеет решение, то есть только два варианта. Либо это решение единственно (и тогда СЛАУ называют определённой), либо этих решений бесконечно много (такую СЛАУ именуют неопределённой). Возникает первый вопрос: как выяснить, сколько решений имеет заданная нам однородная СЛАУ? Одно (нулевое) или бесконечность?
Этот случай уже был рассмотрен в теме «Базисные и свободные переменные. Общее и базисное решения СЛАУ». По сути, однородные СЛАУ – это всего лишь частный случай системы линейных уравнений, поэтому вся терминология (базисные, свободные переменные и т.д.) остаётся в силе.
Что такое базисные и свободные переменные? показать\скрыть
Фундаментальная система решений однородной СЛАУ.
Что значит «линейно независимые решения»? показать\скрыть
В данной ситуации под решением понимается матрица-столбец, в которой перечислены значения неизвестных.
Если система является неопределённой, указать фундаментальную систему решений.
Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.
В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.
Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:
Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №2 и №4:
Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:
Почему меняются знаки? Что вообще значит это перенесение столбцов? показать\скрыть
Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.
А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:
Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.
Записать ФСР однородной СЛАУ
зная общее решение. Записать общее решение с помощью ФСР.
Общее решение уже было получено в теме «метод Крамера» (пример №4). Это решение таково:
Опираясь на предыдущий пример №1, попробуйте составить ФСР самостоятельно, а потом сверить с ответом.
Продолжение этой темы рассмотрим во второй части, где разберём ещё один пример с нахождением общего решения и ФСР.
Однородные системы линейных алгебраических уравнений
В рамках уроков метод Гаусса и Несовместные системы/системы с общим решением мы рассматривали неоднородные системы линейных уравнений, где свободный член (который обычно находится справа) хотя бы одного из уравнений был отличен от нуля.
И сейчас, после хорошей разминки с рангом матрицы, мы продолжим шлифовать технику элементарных преобразований на однородной системе линейных уравнений.
По первым абзацам материал может показаться скучным и заурядным, однако данное впечатление обманчиво. Помимо дальнейшей отработки технических приёмов будет много новой информации, поэтому, пожалуйста, постарайтесь не пренебрегать примерами данной статьи.
Что такое однородная система линейных уравнений?
Ответ напрашивается сам собой. Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например:
Совершенно ясно, что однородная система всегда совместна, то есть всегда имеет решение. И, прежде всего, в глаза бросается так называемое тривиальное решение 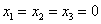
Решить однородную систему линейных уравнений
Решение: чтобы решить однородную систему необходимо записать матрицу системы и с помощью элементарных преобразований привести её к ступенчатому виду. Обратите внимание, что здесь отпадает необходимость записывать вертикальную черту и нулевой столбец свободных членов – ведь что ни делай с нулями, они так и останутся нулями:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3.
(2) К третьей строке прибавили вторую строку, умноженную на –1.
Делить третью строку на 3 не имеет особого смысла.
В результате элементарных преобразований получена эквивалентная однородная система 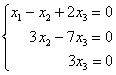
Ответ:
Сформулируем очевидный критерий: однородная система линейных уравнений имеет только тривиальное решение, если ранг матрицы системы (в данном случае 3) равен количеству переменных (в данном случае 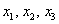
Разогреваемся и настраиваем свой радиоприёмник на волну элементарных преобразований:
Решить однородную систему линейных уравнений
Из статьи Как найти ранг матрицы? вспоминаем рациональный приём попутного уменьшения чисел матрицы. В противном случае вам придётся разделывать крупную, а частенько и кусачую рыбу. Примерный образец оформления задания в конце урока.
Нули – это хорошо и удобно, однако на практике гораздо более распространен случай, когда строки матрицы системы линейно зависимы. И тогда неизбежно появление общего решения:
Решить однородную систему линейных уравнений
Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду. Первое действие направлено не только на получение единичного значения, но и на уменьшение чисел в первом столбце:
(1) К первой строке прибавили третью строку, умноженную на –1. Ко второй строке прибавили третью строку, умноженную на –2. Слева вверху я получил единицу с «минусом», что зачастую намного удобнее для дальнейших преобразований.
(2) Первые две строки одинаковы, одну из них удалили. Честное слово, не подгонял решение – так получилось. Если выполнять преобразования шаблонно, то линейная зависимость строк обнаружилась бы чуть позже.
(3) К третьей строке прибавили вторую строку, умноженную на 3.
(4) У первой строки сменили знак.
В результате элементарных преобразований получена эквивалентная система:
Алгоритм работает точно так же, как и для неоднородных систем. Переменные 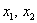
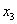
Выразим базисные переменные через свободную переменную:
Ответ: общее решение:
Тривиальное решение входит в общую формулу, и записывать его отдельно излишне.
Проверка выполняется тоже по обычной схеме: полученное общее решение необходимо подставить в левую часть каждого уравнения системы и получить законный ноль при всех подстановках.
На этом можно было бы тихо-мирно закончить, но решение однородной системы уравнений часто требуется представить в векторной форме с помощью фундаментальной системы решений. Пожалуйста, временно забудьте об аналитической геометрии, поскольку сейчас речь пойдёт о векторах в алгебраическом смысле, который я немного приоткрыл в статье про ранг матрицы и окончательно расписал на уроке о линейных преобразованиях. Терминологии тушеваться не нужно, всё довольно просто:
Фундаментальная система решений однородной системы уравнений
Фундаментальная система решений – это множество линейно независимых векторов 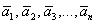
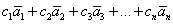
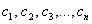
Количество векторов 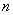
Однако в практических заданиях гораздо удобнее ориентироваться на следующий признак: количество векторов 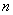
Представим общее решение Примера №3 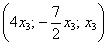
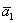
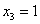
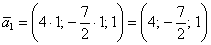
Координаты вектора 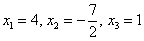
Ответ следует записать в виде линейной комбинации векторов фундаментальной системы. В нашей ситуации линейная комбинация состоит из одинокого слагаемого. Общее решение однородной системы я буду обозначать через вектор 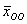
Ответ: общее решение: 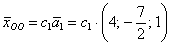
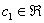
Придавая параметру 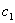
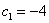
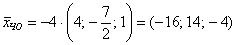
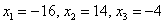
Это мы рассмотрели традиционный способ построения фундаментальной системы в так называемом нормальном виде – когда свободным переменным придаются исключительно единичные значения. Но правила хорошего математического тона предписывают избавляться от дробей, если это возможно. Поэтому в данном случае можно взять 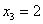
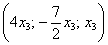
И тогда ответ запишется в эквивалентной форме: 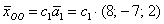
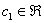
Оба варианта ответа правильны, однако чайникам я всё-таки рекомендую классику жанра.
Поблагодарим задачник Рябушко за предоставленные примеры и перейдём к более основательным системам:
Решить однородную систему линейных уравнений
Ответ записать с помощью фундаментальной системы решений
Самостоятельно, plz. Примерный образец оформления в конце урока.
Закинем в копилку знаний ещё один полезный факт:
Взаимосвязь решений неоднородной
и соответствующей однородной системы уравнений
Представьте двух близких родственниц: неоднородную систему (у которой хотя бы одно число правой части отлично от нуля) и такую же систему – только справа одни нули (то бишь, однородную систему). Нетрудно предположить, что если системы отличаются лишь столбцом свободных членов, то между их решениями должна существовать тесная связь. И это действительно так! Материал целесообразнее рассмотреть на конкретной задаче, которая, как и все другие, взята из реальной контрольной работы:
Дана система линейных алгебраических уравнений
1) найти общее решение;
2) используя результат предыдущего пункта, найти общее решение соответствующей однородной системы и записать его в векторной форме.
Решение: по условию дана обычная неоднородная система уравнений, и первая часть не отличается новизной:
1) Запишем расширенную матрицу системы (не зеваем нолик в третьей строке) и с помощью элементарных преобразований приведём её к ступенчатому виду:
(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на –3. К четвёртой строке прибавили первую строку, умноженную на –4.
(2) Последние три строки одинаковы, две из них удалили.
Обратным ходом метода Гаусса получим общее решение:
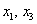
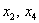
Выразим базисные переменные через свободные переменные. Из 2-го уравнения:
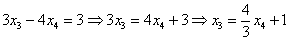
Общее решение неоднородной системы обозначим через 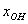
Ответ:
2) Во второй части задания требуется найти общее решение 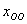
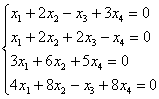
Выполнять элементарные преобразования заново, разумеется, не нужно.
Правило: общее решение неоднородной системы 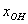
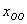
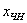
Откуда легко выражается общее решение нашей однородной системы:
Найдём какое-нибудь частное решение 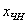
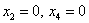
Таким образом, общее решение соответствующей однородной системы:
Представим 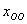
Пойдём классическим путём:
Рассмотрим пару значений свободных переменных 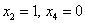
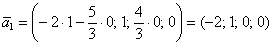
Теперь рассматриваем пару 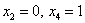
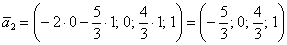
И вообще – любая линейная комбинация векторов фундаментальной системы 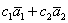
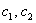
Ответ: 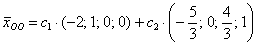
Иными словами, если взять два любых вещественных числа, например, 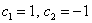
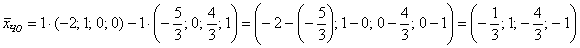
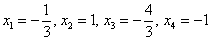
Если хотите избежать дробей, то при нахождении вектора 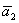
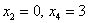
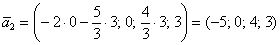
В этом случае ответ запишется в эквивалентной форме: 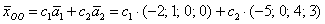
Порядком многих я, наверное, подзапутал, но коль скоро задание не придумано, то его нельзя было обойти стороной.
Более распространённая тема для самостоятельного решения:
Дана однородная система
Найти общее решение и записать ответ с помощью векторов фундаментальной системы. В образце решения завершающим элементарным преобразованием я уже потихоньку начинаю приобщать вас к методу Гаусса-Жордана.
Чтобы окончательно закрепить алгоритм, разберём финальное задание:
Решить однородную систему, ответ записать в векторной форме.
Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:
(1) У первой строки сменили знак. Ещё раз заостряю внимание на неоднократно встречавшемся приёме, который позволяет существенно упростить следующее действие.
(1) Ко 2-й и 3-й строкам прибавили первую строку. К 4-й строке прибавили первую строку, умноженную на 2.
(3) Последние три строки пропорциональны, две из них удалили.
В результате получена стандартная ступенчатая матрица, и решение продолжается по накатанной колее:
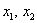
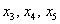
Выразим базисные переменные через свободные переменные. Из 2-го уравнения:
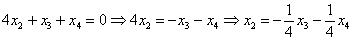
Таким образом, общее решение:
Поскольку в рассматриваемом примере три свободные переменные, то фундаментальная система содержит три вектора.
Подставим тройку значений 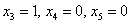
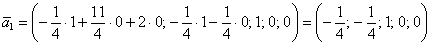
Для тройки значений 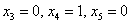
И, наконец, для тройки 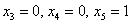
Ответ: 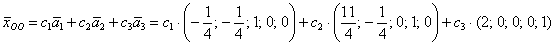
Желающие избежать дробных значений могут рассмотреть тройки 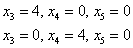
К слову о дробях. Посмотрим на полученную в задаче матрицу 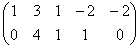
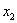
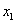
Второй вариант решения:
Идея состоит в том, чтобы попытаться выбрать другие базисные переменные. Посмотрим на матрицу и заметим две единицы в третьем столбце. Так почему бы не получить ноль вверху? Проведём ещё одно элементарное преобразование:
(4) К первой строке прибавили вторую строку, умноженную на –1.
Здесь базисные переменные 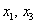
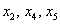
По существу, мы применили метод Гаусса-Жордана, который как раз и направлен на скорейшее получение базисного решения посредством дополнительных элементарных преобразований.
В результате общее решение:
Последовательно выбираем в качестве значений свободных неизвестных тройки 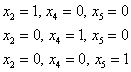
и подстановкой их в 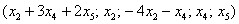
Не забываем проверить координаты каждого вектора!
Ответ: общее решение: 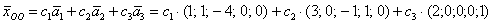
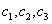
Как видите, второй способ гораздо проще и рациональнее, но для подобных изысков, конечно, необходимо обладать некоторым опытом.
Надеюсь, данная статья окончательно развеяла все страхи перед векторами, и теперь вы с огромным удовольствием откроете учебник по линейной алгебре, чтобы изучить теорию векторных пространств, линейных преобразований и другие не менее интересные вещи.
Пример 2: Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду: 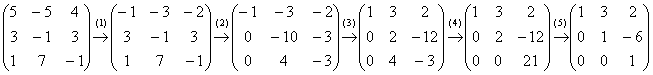
(2) Ко второй строке прибавили первую строку, умноженную на 3. К третьей строке прибавили первую строку.
(3) У первой строки сменили знак. Ко второй строке прибавили третью строку, умноженную на 3.
(4) К третьей строке прибавили вторую строку, умноженную на –2.
(5) Вторую строку разделили на 2, третью строку разделили на 21.
Ранг матрицы системы равен количеству переменных, значит, система имеет только тривиальное решение.
Ответ:
Пример 4: Решение: запишем матрицу системы и с помощью элементарных преобразований приведем её ступенчатому виду: 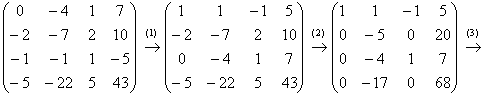
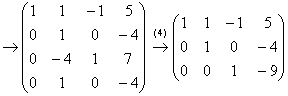
(1) У третьей строки сменили знак и переместили её на 1-е место.
(2) Ко 2-й и 4-й строкам прибавили первую строку, умноженную на 2 и 5 соответственно.
(3) Вторую строку разделили на –5, 4-ю строку разделили на –17.
(4) Вторая и 4-я строки одинаковы, последнюю строку удалили. К третьей строке прибавили вторую строку, умноженную на 4.
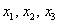
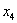
Выразим базисные переменные через свободную переменную.
Из последних двух уравнений:
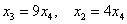
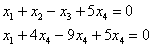
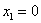
Таким образом, общее решение: 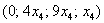
Найдем вектор фундаментальной системы решений. Для этого выберем в качестве значения свободной неизвестной 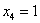
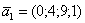
Ответ: общее решение однородной системы уравнений: 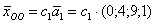
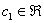
Пример 6: Решение: Запишем матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду: 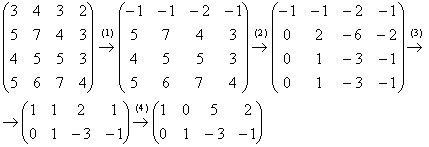
(1) К первой строке прибавили третью строку, умноженную на –1.
(2) Ко второй, третьей и четвертой строкам прибавили первую строку, умноженную на 5, 4 и 5 соответственно.
(3) Последние три строки пропорциональны, достаточно оставить только одну из них. У первой строки сменили знак.
(4) К первой строке прибавили вторую строку, умноженную на –1.
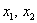
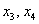
Выразим базисные переменные через свободные переменные: 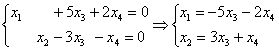
Таким образом, общее решение: 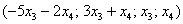
Найдем векторы фундаментальной системы решений. Для этого последовательно выбираем в качестве значений свободных неизвестных следующие пары: 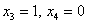
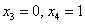
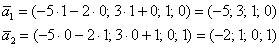
Ответ: общее решение: 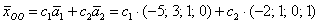
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5